错联齿轮传动应力及啮合刚度分析

张建文 叶友东 蔡志盛

摘要：为了对比普通齿轮传动和错联齿轮传动中应力和啮合刚度的不同，在 Solidworks 中，建立了直齿和错联圆柱齿轮传动模型，将模型导入 workbench的瞬态动力学模块进行有限元分析。结果表明错联齿轮比普通齿轮在传动时的啮合刚度大、承载能力强;错开1/2齿距比错开1/3齿距错联齿轮传动啮合刚度更大、应力应变更小的特点。

关键词：错联齿轮传动;啮合刚度;有限元分析

中图分类号：TH132.4                                   文献标识码：A                                  文章编号：1674-957X（2021）15-0051-02

0  引言

齿轮是机械动力传动中应用最广的一种传动零件，它具有结构紧凑、传递动力大、机械效率高、使用寿命长、工作可靠性好和传动比准确等优点。何育民[1]等通过使用三维建模软件 Solidworks 分析齿轮在仿真中啮合刚度的时变性问题。Zhan 等[2]利用有限元软件 workbench 用准静态方法求解了啮合刚度，并研究了齿顶圆角及主从动轮轴不平行时对啮合刚度的影响。赵庆彬[3]等分析了面齿轮传动啮合刚度问题，验证了理论方法的可靠性，卜忠红[4]运用线性规划法分析了斜齿轮副的时变啮合刚度，阐述了其变动原理。

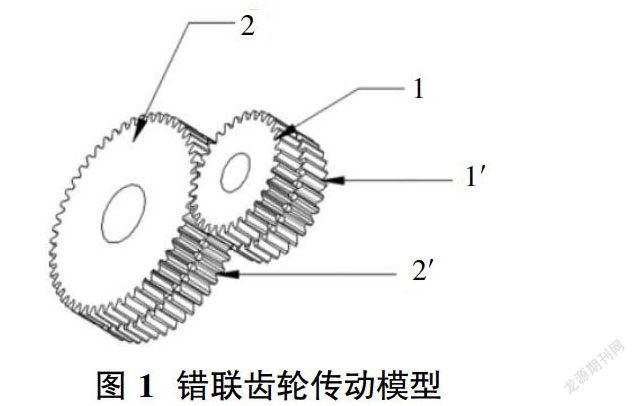
本文提出了由两个错联齿轮相互嚙合组成的一种新型的齿轮传动装置，如图1所示。齿轮1和齿轮1’的参数完全相同，并且两个齿轮彼此沿圆周方向依次错开一定的齿距，如错开1/2和1/3齿距等;齿轮2和齿轮2’的参数完全相同，两个齿轮彼此沿圆周方向依次错开与齿轮1相同的齿距，使得两个错联齿轮相啮合。

1  错联齿轮传动模型的建立及有限元设置

错联齿轮及普通圆柱齿轮建模的参数为齿轮的齿轮1、1’齿数为30，齿宽为30mm;齿轮2、2’齿数为50，齿宽为30mm;齿轮的齿轮3齿数为30，齿宽为60mm;齿轮的齿轮4齿数为50，齿宽为60mm。齿轮的模数均为4，压力角均为为20°，材料为均为45号钢。图1为错联齿轮传动模型。

将齿轮传动装配体模型通过Solidworks与ANSYS workbench的接口直接导入ANSYS workbench的瞬态动力学模块，并且两次分析使用相同的条件[5]。由于每对轮齿啮合图2是主从动轮施加边界条件的过程，左边是主动轮，右边为从动轮，主从动轮轴孔处添加旋转副约束。主动轮旋转副施加10r/min恒定转速，从动轮旋转副施加80N·m转矩，之后进行网格划分和仿真分析[6]。

2  应力分析

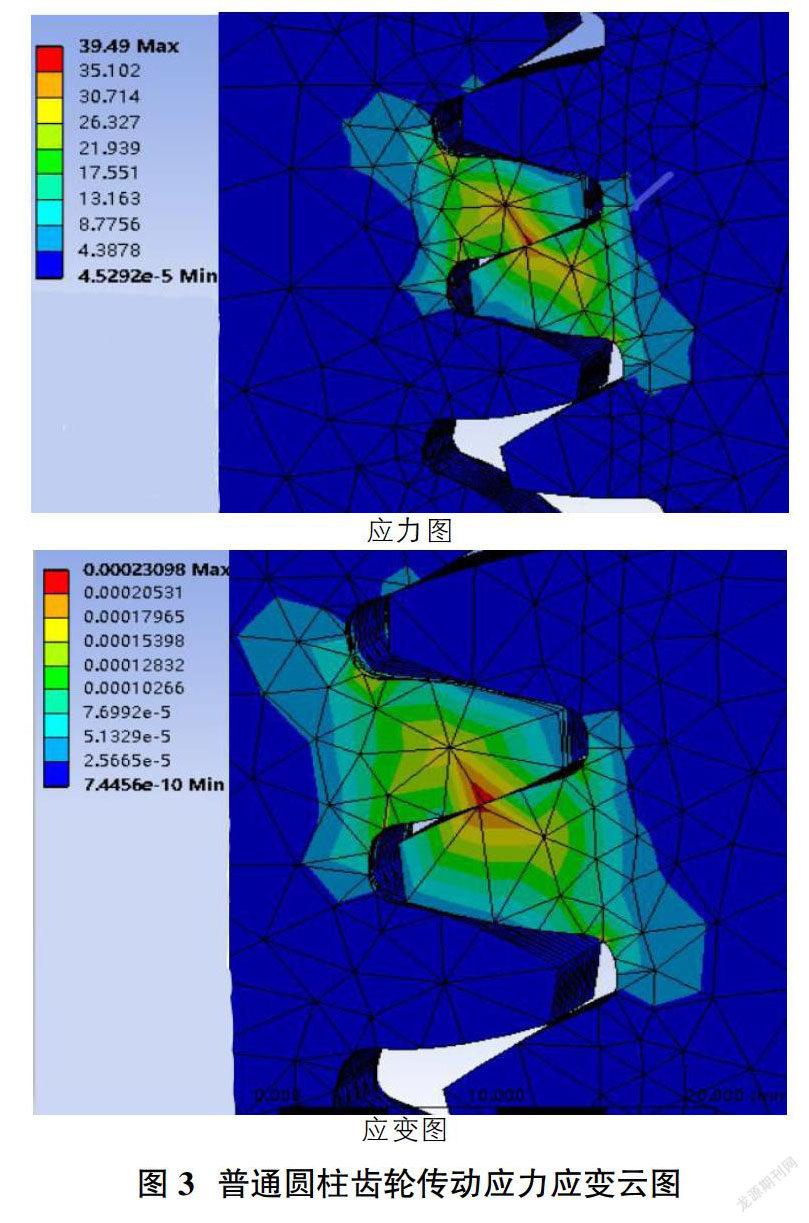
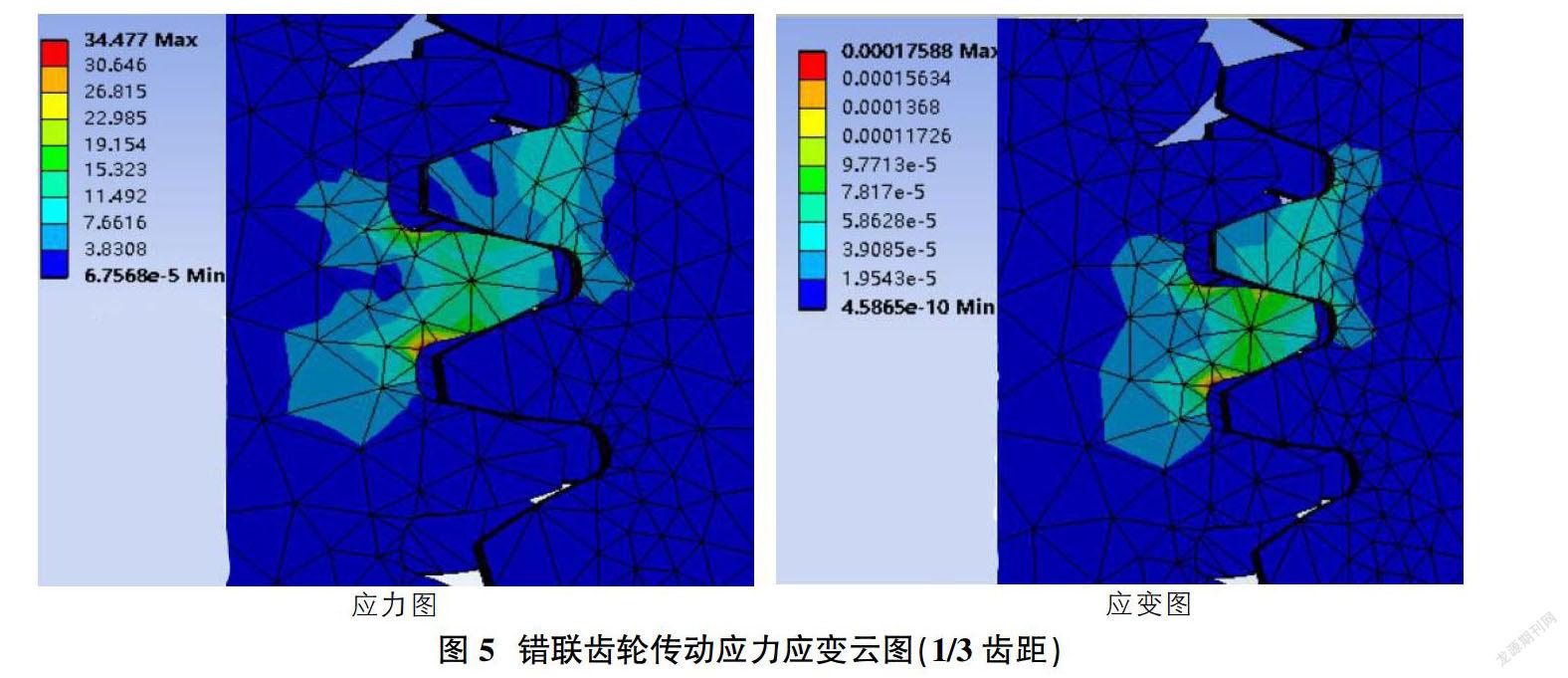
通过有限元分析可以得到齿轮啮合的表面接触应力和应变分布云图，如图3、图4和图5所示，直观地反映了接触应力的分布。从齿轮传动应力云图和应变云图可知，错联齿轮传动与普通圆柱齿轮在传动中的应力和应变更小，承载能力更大。错开1/2齿距比错开1/3齿距齿轮传动的应力和应变都要小，这可以使得错开1/2齿距齿轮在传动过程中可以得到更大的承载力和更小的变形。

3  啮合刚度分析

根据文献[7]可得准静态下啮合刚度表达式为：

仿真完成后，提取主从动轮的转角，得到动态传递误差，计算出啮合刚度。为了体现这种规律，引入无量纲啮合时间 t/tc，t是绝对时间，tc是轮齿沿啮合线移动一个分度圆法向齿距的时间。

从图6可知，齿轮的啮合刚度是周期性变化的，错联齿距的齿轮在啮合时产生的冲击和传动的平稳性都要优于普通的圆柱齿轮，它可以降低齿轮运行时的突变程度，使传动更加平稳，增加承载力;错开1/2齿距齿轮与错开1/3齿距齿轮相比在啮合时产生的波动小，刚度更大，在传动过程中更平稳，错开1/2齿距齿轮比错开1/3齿距齿轮更适用与传动。

4  结论

建立齿轮传动模型，并通过有限元方法仿真得到错联齿轮传动和普通圆柱齿轮传动的应力与啮合刚度曲线，仿真结果发现，轮齿啮合过程中，由于啮合刚度的时变性会产生频率为啮合频率的周期性冲击响应，错联齿轮在运行时的应力、应变和刚度变化都要优于普通圆柱齿轮;错开1/2齿距齿轮与错开1/3齿距齿轮相比承载能力和平稳性更好。采用错开1/2齿距齿轮可以降低啮合刚度的突变程度使运行更加平稳，减少振动，来达到优化齿轮振动特性的目的。

参考文献：

[1]何育民，郝安帮.基于ANSYS workbench齿轮啮合刚度计算及动力学仿真[J].沈阳工业大学学报，2020，42（02）：191-196.

[2]Zhan J X， Fard M， Jazar R. A CAD-FEM-QSA integ-ration technique for determing the time-varying me-shing stiffness of gear pairs[J]. M easurement， 2017， 100： 139-149.

[3]赵庆彬，刘海军，李晓贞.面齿轮传动啮合刚度分析[J].机械传动，2014（7）：6-9.

[4]卜忠红，刘更，吴立言.斜齿轮啮合刚度变化规律研究[J].航空动力学报，2010，25（04）：957-962.

[5]张双伟，于文军，金亮，等.基于有限元法的齿轮啮合刚度分析[J].黑龙江科技信息，2016，24（24）：114-115.

[6]白恩军，谢里阳，佟安时，等.考虑齿轮轴变形的斜齿轮接触分析[J].兵工学报，2015，36（10）：1975-1981.

[7]郝安帮.啮合刚度影响因素研究及齿轮动力学仿真[D].西安建筑科技大学，2018.