巧用类比进行高中立体几何解题

2021-09-10苏宁

高考·上 2021年2期

苏宁

摘要：立体几何内容在多次课改后仍作为数学重要内容之一，而且从高中内容和高考试题所占的比重来看，进行立体几何解题研究是非常必要的。已有研究表明，类比是立体几何解题众多思想中的一种。本文将围绕如何运用类比进行立体几何解题展开研究。

关键词：类比;立体几何;解题

作为自然科学的基础，数学的发展一直被人们看重。这表现为数学一直是我国基础教育阶段的基础学科之一，也表现为在各级各类形式的考试中，数学都是一门必考科目。尤其是高考，数学作为高考的一门必考科目，考虑到它在高考中所占比重，数学的重要性不言自明。数学涵盖了众多的知识模块，每个模块都应被深入地进行解题研究。其中立体几何历经数次课改，仍占据着高中数学无可撼动的重要地位。考虑到一些实际原因，现实表明立体几何一直是学生们学习的重点和难点之一。

基础教育阶段教材的編制也考虑到这个问题，为分解学习难度，我们从小学阶段就开始接触到立体几何。国内在每个阶段都安排有立体几何知识的学习，循序渐进式学习是非常好的，但是学习难度仍然存在。具体来说，空间几何的抽象性较大，真正解决立体几何问题主要集中在高中阶段，这要求学生必须具有一定的演绎推理能力与空间想象能力，但这又是学生欠缺的。好的立体几何教学策略固然会得到好的教学效果，掌握立体几何解题方法非常重要。如果按照波利亚的说法，掌握数学就意味着善于解题的话，那么，我们也可以说，衡量掌握好立体几何的一个重要标准就是要擅长立体几何解题。

众所周知，类比是一种重要的数学思想。它可以加强数学新旧知识间的联系，梳理数学知识，深化对问题的认识，开阔自身的视野，进而深化学生对于这种思想的认识，提高学生自身发现问题的能力。已有研究表明，类比是立体几何解题众多思想中的一种。姚宗贵在其文章中提出，在立体几何中，类比这种思想方法的应用也是比较广泛的，并列举了大量例子。在立体几何的相关解题中，如果巧妙使用类比，可以降低问题的难度，方便学生解答。以下将列举一些具体题目供读者体会：

例1：通过类比将平面几何命题推广到空间得到立体几何命题如：在平面几何中，正三角形内任意一点到三边的距离之和为定值。类比到立体几何中有什么结论呢？分析“正三角形”类比到空间“正四面体”任意一点到三边的距离之和为定值类比到空间为“任意一点到四个面的距离之和”是否也是一个定值呢？

解析：类比平面的线到空间的面，平面的面到空间的体。结论：任意一点到四个面的距离之和为定值。解决方法：联想平面中结论的证明应用的是等面积，则空间中使用等体积来处理。

例2：类比平面直角三角形的勾股定理，试给出空间中四面体性质的猜想，并证明。

解析：类比线的关系得到面的关系。猜想面积的平方之间具有某种等量关系。类比平面中的直角三角形，得出的结论是适用于特殊的空间四面体，即直三棱锥（也就是俗称的“墙角”）。猜想：三个两两互相垂直的面构成的四面体中，剩余的面的面积的平方为这三个两两互相垂直的面的面积的平方和。

例3：能否将平面中的中位线定理推广到立体几何中？

解析：运用类比可将平面几何中的中位线定理按照下述方式推广到立体几何中的关于棱锥中位面的命题：在一个四面体中，三个侧棱的中心所构成的三角形即为该四面体的中位面，中位面的面积为底面面积的四分之一。在类比得到命题之后，证明就比较简单了，这个问题的关键点是通过类比，构建一个新的命题。

例4：试给出定理：“在同一个三角形中，任两边之和大于第三边。”在立体几何中的一种推广，并证明推广后的命题。

解析：类比二维平面中的“三角形”与三维空间中的“四面体”，首先可以做出如下推广：在同一个四面体中，任意三个面的面积之和大于第四个面的面积。在我们通过类比得到命题后，我们再继续进行命题的证明就简单多了。

例5：直线（或线段）可以看成一维，平面是二维的，几何体是三维。由此：线段的中点平分线段，即分线段的比是1：1，三角形的重心分所在的中线1：2，已知：四面体ABCD，△BCD的重心为E，△ACD的重心为F，AE交BF于点O，则O分EA的比为_____。

解析：类比平面中重心的比例关系的证明，同样可以构造平行线去证明空间中的比例大小。连接AF、BE、EF即可获得O分EA的比为1：3。

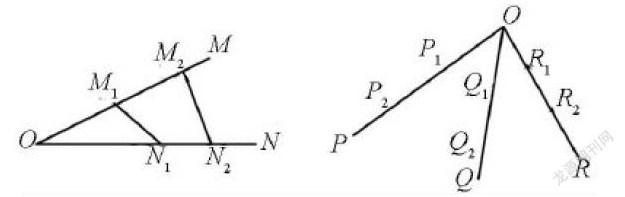
例6：如图所示，若从点O所做的两条射线OM、ON上分别有点M1，M2与点N1，N2，则三角形的面积比为，若从点O所作的不在同一个平面内的三条射线OP、OQ和OR上，分别有点P1、P2;Q1、Q2;R1、R2，则类似的结论为______。

解析：新旧知识的类比有内容上的对比，有方法上的对比，也有基本结构上的对比，通过类比可以使扑朔迷离的问题明朗化。本题易见是以三角形作为类比对象，将所求的问题迁移到立体几何中，继而得出三棱锥的体积比为。

例7：直角三角形ABC中，下述命题是成立的：

①∠A=30°，则其所对边;

②若CD是斜边上的中线，则

③若CD⊥AB于D，则CD是BD与DA的比例中项。

在直三棱锥O-ABC（俗称“墙角”）中，有类似的命题成立：

①若AO与面ABC成30°，则S△BOC_____;

②E、F分别是侧棱AB、AC的中点，则S△EOF______;

③过O作平面ABC的垂直平面β，设β交面ABC于AD，且OA与面ABC成α角，则_____________。

解析：本题的意图是在平面中三个定理的基础上，根据相应的定理内容，运用类比推导出空间立体几何中与之相对应的定理的内容。设置的问题既从解题过程中依赖前面的结论，也从结果形式上类比前面的结论得到对应形式。①中平面给出的是边之间的关系，转移到空间中去，类比得到面积之间的等量关系。题目条件有线面角，依据此寻找面积表达式中边长的比例关系，即S△BOC=S△BOC.②是在第①步的基础上，继续寻找面积计算公式中边和高之间的比例关系。当然面积的关系需要利用平面中线段之间的关系，进一步得到S△EOF=S△ABC.。③小题类比平面中的射影定理，根据表达式中的边长，扩展成面积时，为保持等量关系，需要平方，这个是相较前面的稍复杂一点的类比，即S△OAD2=S△ABD· S△ACD· cos2α.

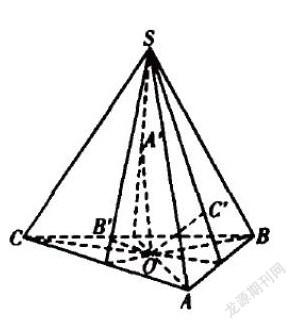
例8：由三棱锥S-ABC的底面ABC上任一点O作直线OA'，OB'，OC'分别平行于棱SA、SB、SC与面SBC、SCA、SAB相交于A'，B'，C'。

求证：。

解析：本题的证明与在平面几何中证明这类式子相类似。通常的处理方式是把左边的几个式子转化为面积比后再证。在立体几何中，用类比的方法解决问题时需设法把等式左边化为体积之比，在分母相同的情况下，化简各式证明本题。

例9：如图所示，ABC-A1B1C1为一斜三棱柱，点P为ABC-A1B1C1其中一條侧棱BB1上的任意一点，过点P分别作垂线PM垂直于AA1，PN垂直于CC1，垂足分别为M，N，连接MN。

（1）证明：MN垂直于CC1;

（2）任意给△DEF，由余弦公式知：DE2=DF2+EF2-2DF·EF·cos∠DFE现将此公式拓展到空间图形，类比平面三角形的余弦定理，推测斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式，并给出相应证明。

解析：（2）题考查平面中三角形的余弦定理在空间图形中的推广，其中联系的线索为余弦定理。这里的类比主要是从平面中的线类比到空间中的面，两条线的交角类比到空间两个面所成的二面角。由（1）知，可以使用余弦公式得出 PM2=MN2+PN2-2·PN·MN·cos∠PNM，两边同乘以CC12，即可得到斜三棱柱三个侧面的面积，于是得证。

以上的分析研究对使用类比快速解决立体几何问题是有重要意义的。学习虽苦，但是如何苦中作乐，让自己从浩瀚的知识海洋中体会获取知识的快乐，体会解决困难后的喜悦，体会到高效学习的痛快，这对学生来说将是非常珍贵的。具体笔者给出下面几点建议：

一、不断建构立体几何知识体系

不断将所学知识进行关联，在掌握类比和立体几何的基础知识后，尝试建构立体几何知识体系。避免学生将知识孤立起来学习，学生自己也可以了解，任何待解决的数学问题都是可以通过什么样的知识链接起来，而且连接起来的知识之间是通过什么连接起来的，这会给我们一些做题的灵感，在我们平时的解题中为我们指明方向。

二、挖掘类比和立体几何知识背后更深的内涵

鉴于学生处理复杂的类比题目解决立体几何问题的作答情形，仅仅教授学生基础的知识是远远不够的。单纯地形式上的类比，结果有可能是错误的。我们需要可靠地借助类比解决问题，这样自然会收获到更多的知识。

三、严格要求自己，不断提高自身能力和素质

学生功利化的学习一直是教育中不可规避的问题，学生们长久的停留在重复训练相同的或者相似的题目，难以得到自身能力的提升。要正视学习，学习是为了不断地提高自身能力，加强个人修养。

四、多思多想，养成独立思考的习惯

好的解题就要达到做一反三的地步。如不能灵活挖掘题目的本质，则很难达到很好的解题。有人说数学有一种“冷峻而严厉的美”，想要挖掘出数学的这种美，需要学习者不断地进行思考，将自己对问题的认识纳入到自己的知识体系中去，只有这样才能不断的进步。

参考文献

[1]姚宗贵.立体几何教学中渗透数学思想方法的研究与实践[D].河南大学，2013.

[2]杨建仁.基于类比思维的高中数学解题方法研究[J].数学学习与研究：教研版，2013（第7期）.