逆向思维在初中物理解题中的应用

汤中华

摘 要：通过运用逆向思维，初中生可以在解答物理问题的时候更活跃地探究其解答关键线索，迅速理性题目中不同信息之间存在的联系，实现高效整合碎片讯息，用更方便的方法实现对于题目的求解过程.

关键词：逆向思维;初中;物理;解题应用

初中生们在学习物理知识的时候，往往需要运用所学知识解决各种问题，而很多问题的解决方案相对复杂繁琐，学生很难迅速找到解答关键线索.而通过运用逆向思维方式，学生们往往能够从另一个角度进行已知条件分析，从而另辟蹊径，顺利完成解答.接下来，笔者将从多个方面简单分析逆向思维在初中物理解题中的一些关键应用技巧方法，提升学生们的物理解答能力跟思维能力.

一、运动问题的逆向思维应用

跟运动相关的物理问题经常会用到逆向思维进行解答，因为对于初中生们而言，他们接触物理这门学科的时间还不算很长，虽然有些知识都学习过了，但是在实际做题的时候，出题人一旦有所改变，将物体运动状态进行修改，学生们就不知道该从何处下手了.而运用逆向思维能力，我们从运动状态末端往回推導，慢慢还原到“初态”，这样能够更好地帮助学生理清物体所做运动的特点，也符号他们所学的知识最初形态.比如，我们将做加速运动的物体倒着看，就是一个减速运动，而作减速运动的物体按照逆向思维就变成了了加速运动，具体应用哪种方法，学生要针对题目特点以及自己的学习情况有所变通，尽可能地将复杂的物体运动过程简化，按照自己最好理解的方式进行转化.

例题：有一辆装满货物的卡车，总重量为35000N，载着货物以10米每秒的速度匀速行驶在水平的路面上，当卡车匀速行驶十分钟后，已知其受到的阻力为3000N，试求在卡车行驶的十分钟内，发动机所产生的牵引力对车作用为多少？卡车功率为多少？

我们在分析本问题的时候，如果按照常规思维进行探究，很容易就会受到卡车总重量为35000N这个数字的干扰，其实在本题目当中，并没有用到这个数.从逆向角度出发，我们首先利用距离计算公式S=VT计算出在十分钟内卡车行动总距离是10

m/s×60×10s=6000m.而在匀速运动下，根据“力的作用是相互的”这一定理，我们就可以很迅速推导出：卡车受到的牵引力与阻力应该是相等关系，即F=f=3000N，牵引力对卡车作用W=Fs=3000N×6000m=1.8×107J，功率P=Wt=30000W，完成解答.利用逆向思维，初中生有效规避开了题目中存在的干扰项，从所求推导已知，顺利找到了牵引力、阻力、功率之间存在的必然联系.多加锻炼，学生们转化思路的能力跟速度都会大大加强，准确地找到问题解决突破口提升做题效率，自我做题信心也慢慢加强.

二、磁场问题的逆向思维应用

逆向思维法就是要求写题人从题目已经给出的条件出发一步步探索，在中间需要找到哪些条件才能满足最后的求解问题？在解题的过程当中，我们需要不断向自己发问：我们最终要得到怎样的数据？在得到这样的数据时需要怎样的条件？如果我们已经得到了，满足该数据的条件，那么将其当作最终结论，条件均满足？在初中阶段，虽然我们接触到的大部分知识都是具象的生活中常见现象.但是也会存在一些我们看不见摸不着的物理现象，比如磁场，电场等等，为了探究这类物理知识，学生们更要巧妙运用物理规律之间的因果关系进行理解与学习.

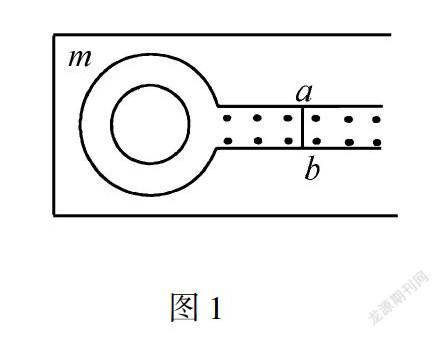
图1比如，如图1所示，现假设在一个匀强磁场当中，我们放入一电阻不计的平行金属导轨，导轨跟大线圈m相接，在导轨上放置裸体导线ab，要想让m上的闭合线圈产生顺时针方向感应电流，需要导线ab如何运动？

为了判断出导线ab运动方向，可根据右手定则.这样就可以很迅速的判断出导线的运动状况应该是向右运动.

三、浮力问题的逆向思维应用

在浮力问题中，最为关键的知识就是浮力计算公式：F浮=ρ液gV排，当物体受到浮力作用以后，如果物体本身不发生任何改变，那么在同一个g下的浮力大小自然也不会有任何改变.学生们在尝试着解答浮力相关问题的时候，也要把握好这一知识进行逆向思维应用，尽可能地实现从反方向将最终结果的正确与否判断出来，一步一步完成详细答案数字的求解.

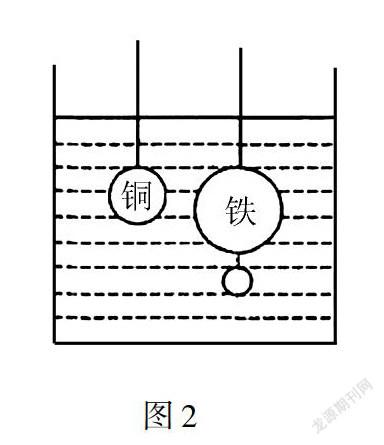
例2 现有两个金属实心小球，如图2所示，分别由铜跟铁制作而成，我们现在将这两个小球用一个重量跟体积可忽略不计的细线系在两个相同的测力计下面，然后将小球完全浸入水中，此时两个测力计所显示的数据完全相同，那么在我们将小球提出水面以后，哪个示数会更大？

本题目所描述的实验过程还是比较清楚的，但是学生们往往不习惯这种比较两个重新从水中拿出小球质量大小的题目，我们就可以引导学生们用逆向思维重新设计一个相反的实验过程：假设两个小球在提出水面以后的重量相同，那么根据浮力计算公式：F浮=ρ液gV排，体积更大的铁球必然所收到的浮力更大一些，要想让两个测力计示数相同，还需要给铁球方多加挂一些东西.故而，顺势完成了原本题目的解答：若两个测力计所显示的数据完全相同，那么在我们将小球提出水面以后挂有铁球的测力计示数会更大.当我们善于运用逆向思维进行题目改装以后，往往可以在解答一道题的时候设想出多个不同解答方法，拓展了思维的同时也能够进一步品尝到解答题目思考过程的乐趣所在.

四、电学问题的逆向思维应用

如果有人想要发明一种既能够节省功，又可以节省力的机械，我们就可以告诉他这是不可能的.而为什么我们能够迅速得出这样的一个结论呢？这其实就是对于逆向思维最简单而直接的应用.根据我们曾经学习过的“功的原理”，功与力的存在是相辅相成的，进而根本就不可能存在既省功又省力的新型机械.我们在解决电学问题的时候，也需要尝试着使用逆向思维进行解答.在初中阶段学生们往往都是计算在理想情况下，也就是忽略电线对于电能损耗情况的各种问题.因此，学生们在尝试着回答问题之间，一定要从根本入手，仔细分析电路实际情况，然后找到在本题目中不会发生改变的常量.例如，在串联电路中的电流、并联电路中的电压、家庭电路中的220V交流电等等，这些都是不会发生改变的常量，把握好所要求解问题与这些恒量之间的关系，再运用逆向思维，就可以很容易完成解答.

比如，当电灯的灯丝发生断裂以后，我们再将灯丝重新接上会发现电灯泡比原先要更加明亮，这是因为什么原因的？为了回答这个问题，学生就可以试着利用逆向思维从结果入手进行分析，产生问题的根本原因是接好灯丝以后的灯泡更加明亮，那么能导致灯泡明亮的因素是因为电压或者电流发生了改变.在家用电路中电压已知为恒定的220V交流电，所以必然是电流增大才导致的灯泡亮度增大.我们再根据这一线索推到公式U=IR，灯丝的电阻减小了，学生很容易就可以想到了在灯丝发生断裂以后，重新进行灯丝连接，那么灯丝长度确实是要变短，这便是电阻减小的原因.通过逆向推导，我们很顺利地完成了本题解答.除此以外，学生们其实还可以从功的角度分析问题，由公式P=U2R可知，灯泡亮度变强是因为实际功率P增大的缘故，故而电阻R变小才导致了这一现象.学生们在解答实际电学问题的时候，可以采用的方法不尽相同，但是一定要在启用逆向思维之前找好问题中存在的各种逻辑关系，这样子才能够顺利逆向完成每一个关键线索的探究以及最终问题的解答.

综上所述，在初中物理教学过程当中，教师应当在传统教学模式之上不断做出改进，善于引导学生用逆向思维方法分析物理问题.在初中生用常规方法解答物理问题受阻的时候，可以尝试着从多个角度找寻题目中已经给出的关键因素，从未知推已知，保证物理问题求解过程始终拥有明确的目标，提升自己解题效率，增强物理知识水平.

参考文献：

[1]王超.浅谈初中物理教学中逆向思维培养[J].才智，2020（06）：148.

[2]张娅.物理教学激发学生“求异思维”之探微[J].课程教育研究，2018（02）：160.

[3]王金伟.逆向思维在初中物理教学中的应用[J].课程教育研究，2018（01）：165.

[责任编辑：李 璟]