由一道高考解析几何题的探究所引发的思考
2021-09-10王江河
王江河



摘 要:圆锥曲线是高中数学的重点和难点,也是高考数学考查的热点,圆锥曲线问题涉及知识点多,解题方法灵活多变,题型丰富,用几何画板探究题型变化,便于直观研究点、直线、曲线之间的各种关系,完美的做到动静结合、数形结合,有助于师生优化解题策略、提高数学思维品质。
关键词:几何画板;圆锥曲线;数形结合思想;特殊与一般思想
笔者在探究本试题时,把此题做一般化考虑(文中变式3),用几何画板探究,发现椭圆中有定直线与定点对应,进一步引发更多地思考,椭圆思考完,想到圆是否有此性质?笔者通过设置条件和调整点或直线位置,发现类似性质.最后想:圆锥曲线中心对称图形中的双曲线也是否有类似性质,结论是肯定的.但回过头思考,应该圆的性质在前,类比到椭圆,再到双曲线更自然,故本文把圆的探究题置于前面.
题1.已知圆O的直径AB,圆上不同于A、B的两点C、D,如果直线AC与BD相交于点M,直线AD与BC相交于点N,则直线MN与直线AB垂直.
探究:分两种情况:(1)当C、D两点在直线AB同侧,直线MN与圆相交.(2)当C、D两点在直线AB两侧,直线MN与圆相离(图略).
变式1.已知圆O直径AB,直线l与线段AB垂直于点G,点M是直线l上任一点(不同于点G,不同于直线l与圆O的交点),直线MA与圆O交于点C,直线MB与圆O交于点D.
(1)若直线CB与直线AD相交于点N,则点N一定在直线l上.
(2)当点M在直线l上运动时,直线CD过定点(即动直线CD与定直线AB的交点)(图1).
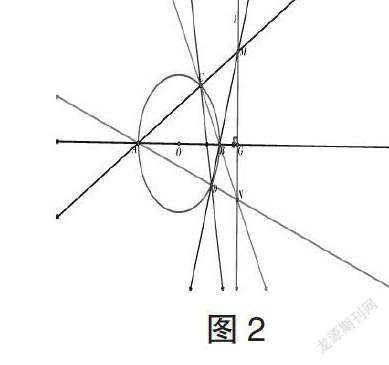
变式2.已知圆O的直径AB,直线l与线段AB(或BA)延长线垂直于点G,点M是直线l上任意一点(不同于点G),直线MA与圆O交于点C,直线MB与圆O交于点D
(1)若直线CB与AD相交于点N,则点N在直线l上(图2).
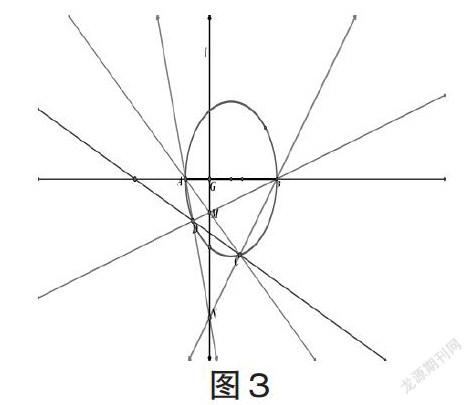
(2)当点M在直线l上运动时,直线CD过定点(即动直线CD于定直线AB交点)(图3).
反思:题1与变式1、变式2不知道哪个是正向思考,哪个是逆向思考,由于定点与定直线相互牵制,线对应点,点对应线,密不可分,故只需变化条件,这3题无所谓哪个先哪个后.
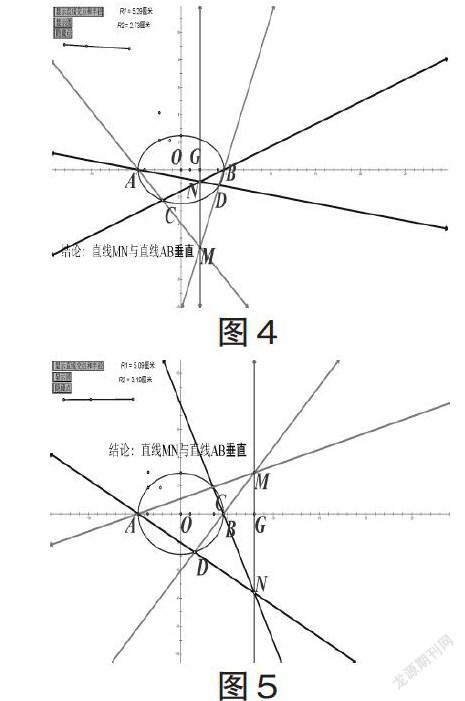
题2.已知椭圆C1的长轴两端点A和B,椭圆上不同于A、B的两点C、D,如果直线AC与BD相交于点M,直线AD与BC相交于点N,则直线MN与直线AB垂直.
探究:分两种情况.
(1)当点C、D在直线AB同侧时,直线MN与椭圆相交(图4).
(2)当点C、D在直线AB两侧时,直线MN与椭圆相离(图5).
变式3.已知椭圆C1的长轴两端点A和B,直线l与线段AB垂直于点G,点M是直线l上任意一点(不同于点G,不同于直线l与椭圆C1的交点),直线MA与椭圆C1交于点C,直线MB与椭圆C1交于点D.
(1)若直线CB与直线AD相交于点N,则点N在直线l上(图6).
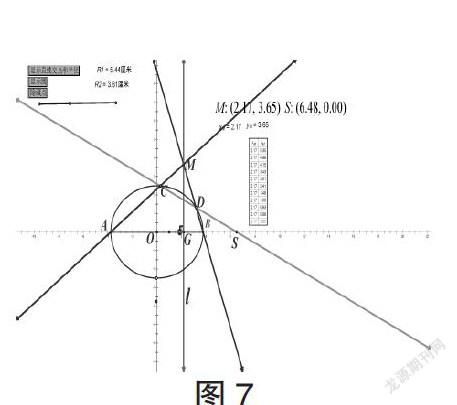
(2)当点M在直线l上运动时,直线CD过定点(即动直线CD与定直线AB的交点)(图7).
反思:变式3能否逆向思考,由定点S得到定直线呢?
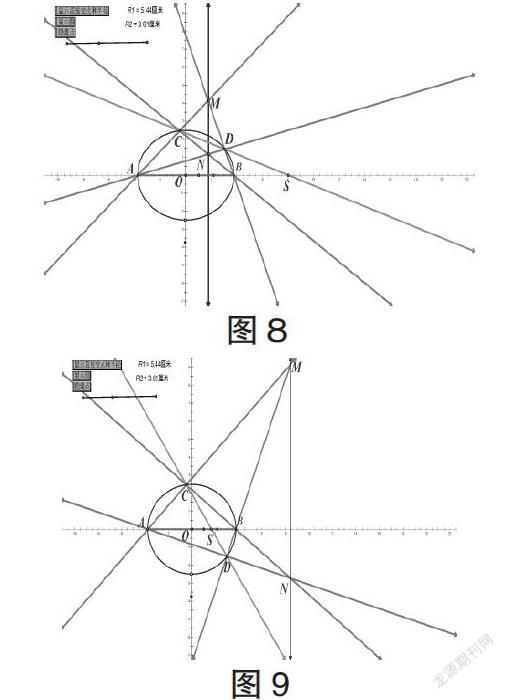
变式4.已知椭圆C1的长轴两端点A和B,直线AB上有定点S,过点S的直线与椭圆交于点C、D两点,若直线AC与直线BD交于点M,直线AD与直线BC交于点N.则直线MN与直线AB垂直(图8,图9).
反思:长轴有此性质,短轴有吗?几何画板强大的作用让我們得到了肯定的结论.
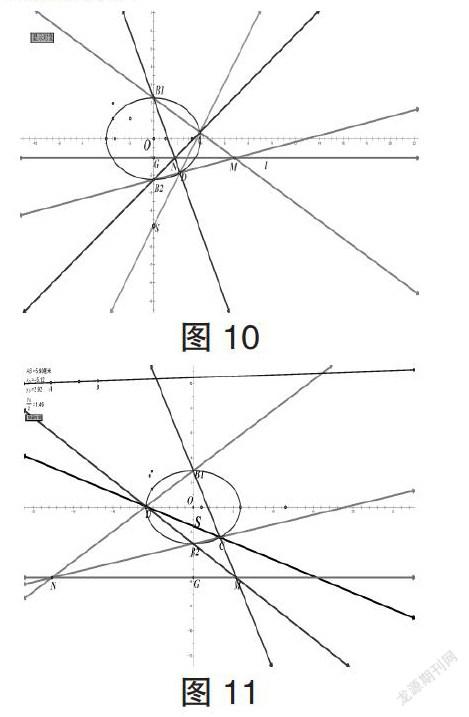
变式5.已知椭圆C1的短轴两端点B1和B2,C、D两点是椭圆C不同于B1、B2两点,直线B1C与直线B2D相交于点M,直线B1D与直线B2C相交于点N,则直线MN与直线B1B2垂直.(图10,图11).
变式6.已知椭圆C1的短轴两端点B1和B2,直线B1B2有定点S,过点S的直线与椭圆C1交于点C、D两点,若直线B1C与直线B2D交于点M,直线B1D与直线B2C交于点N.则直线MN与直线B1B2垂直(图10,图11).
反思:双曲线有此性质吗?几何画板画图探究再开始.
变式7.已知双曲线C2的实轴两端点A1和A2,直线A1A2有定点S,过点S的直线与双曲线C2交于点C、D两点,若直线A1C与直线A2D交于点M,直线A1D与直线A2C交于点N.则直线MN与直线A1A2垂直(图12,图13).
变式8.已知双曲线C2的实轴两端点A1和A2,C、D两点是双曲线C2上不同于A1、A2的两点,若直线A1C与直线A2D相交于点M,直线A1D与直线A2C相交于点N.则直线MN与直线A1A2垂直(图12,图13).
变式9.已知双曲线C2的实轴两端点A1和A2,直线l与直线A1A2垂直于点G(不同于A1和A2),点M是直线l上任意一点(不同于G,不同于直线l与双曲线C2的交点),直线MA1与双曲线C2交于点C,直线MA2与双曲线C2交于点D.
(1)若直线A1D与直线A2C相交于点N,则点N一定在直线l上.
(2)当点M在直线l上运动时,直线CD过定点(即动直线CD与直线A1A2的交点)(图12,图13).
如果顶点为双曲线两个虚顶点呢?思考可以继续,探究还可进行.
本文笔者只是从几何画板角度下探究了高考试题,引发了一系列思考,由于篇幅,本文略去证明过程,不当之处望各位同仁指正。笔者在探究中真正的领悟了数学中的各种美:动与静的结合美、数形结合的图形美、类比推理的思维美等,我们的一线教师可以把这种思考和训练形式用到课堂,真正让学生喜欢上数学,这也是我们数学教育工作者的任务和责任.
参考文献
[1]田保.圆锥曲线两垂直相交弦中点连线的性质——一道高考模拟题的思考和探究.中学教学参考,2019(29):6-7.
