浅以“人船模型”为例，谈科学思维的培养

杨丽红

摘 要：在高中物理模型的教学过程中，需要合理的设置问题，培养学生建构模型、科学推理、科学论证的思维能力。本文中以人船模型为例，以学生科学思维发展水平为导向设置变式训练，逐层培养学生的科学思维。

关键词：科学思维;人船模型;变式训练

在《普通高中物理课程标准（2017）》中提到的物理学科核心素养涵盖了物理观念、科学思维、科学探究和科学态度与责任四个维度，其中提到的科学思维被分为五个水平[1]，每个水平的要求在逐层提高。因此，在物理模型的教学中，需要经过模型分析构建，由浅入深，设置变式训练，循序渐进，引导学生掌握其特点、规律和实质，进而培养学生的科学思维。

动量守恒定律是高中物理的重要内容，“人船模型”是守恒定律应用问题中典型的物理模型。下面以人船模型为例结合科学思维建立、培养，具体分析如下：

一、原型呈现

如下图1所示，质量为m1、长度为L的船停在静水中，质量m2的人静止在船头，当人从船头走到船尾的过程中，求船对地的位移（不计水对船的阻力）。

分析：以人和船组成的系统作为研究对象，在人从船头走到船尾的过程中，由于不计水对船的阻力，系统在x方向上合外力为0，所以在x方向上系统动量守恒。以人运动的方向为正方向，系统的初总动量为0，由动量守恒定律得：

m1v船-m2v人=0

由等式可知，当人向前加速运动时，船同时向后也做加速运动;当人向前匀速运动时，船同时向后也做匀速运动;当人向前减速运动时，船同时向后也做减速运动;当人停止运动时，船也同时也停止运动。设整个运动过程中人对地的平均速度为，船对地的平均速度为，则有：

m1-m2=0

而对地位移：，即有：m1v船-m2v人=0;

画出此过程的运动情景图如图2：

由图可知：x人+x船=L，联立以上，解得x船。

该模型研究对象是人船两物组成的系统，由于系统在x方向上合外力为0的情況下，所以x方向上动量守恒。此模型涵盖了物理观念中的水平1、2、3，能从物理学的角度观察、描述和解释自然生活现象，有物理与实际相结合的意识，并用物理知识解决实际问题[1]。该系统在相互作用下各自运动，在x方向上动量始终守恒，体现了科学思维素养中的水平1、2，也就是能对常见的物理现象能够结合物理知识进行简单分析，进一步能对简单的物理现象结合物理学知识进行分析推理并获得相关结论[1]。

二、设置模型变式训练，建立科学思维

（一）训练一

如图3底边长为b、质量为M的斜劈静止于光滑水平面上，有一个质量为m的滑块从斜劈顶部静止释放滑到底部时，求斜劈的位移。

分析：以斜劈和滑块组成的系统为研究对象，滑块由斜劈顶部无初速度滑到底部的运动过程中，系统水平方向动量守恒，两者在水平方向上对地的位移满足“人船模型”的位移关系。设斜劈移动s，则由水平动量守恒得：

解得：

题中系统在相互作用下各自运动，系统的初动量为0，运动过程中系统x方向上不受外力，系统在x上动量守恒，即可视为“人船模型”，应用该模型中两物的位移关系则可快速得解。把斜面上物体运动的问题和人船模型的特点对照分析，把问题归类到熟悉的物理模型中，这属于科学思维素养水平2、3层次的培养，即能从不同的角度思考问题，对简单的物理现象进行分析、推理，用已有的实用证据模型结合分析并得到结论[1]。

（二）训练二

一质量为m1的载人气球开始静止在离地为H的空中，质量为m2的人要沿气球绳梯缓慢滑至地面，求绳梯的最小长度。（不计空气阻力、软绳梯质量。）

分析：以气球与人组成的系统为研究对象，系统在y方向上不受外力，系统在相互作用下各自运动，在整个运动中y方向上动量守恒。可类比x方向动量守恒的人船模型。设细绳的最小长度为l，以人的对地运动方向为正方向，当人向下滑至地面时，向下运动的距离为H，同时气球向上移动，气球对地上升的高度应为（l-H），如图4所示，由动量守恒定律得：

解得：

题中人与气球的系统在相互作用下各自运动，运动过程中系统任始终都不受外力，系统在y上动量守恒。属于竖直方向、系统总动量始终为零的“人船模型”，有人向下运动，同时气球向上运动、人加速球加速，人减速球减速、人停球停等与“人船模型”一致的有关速度、位移关系的结论。这属于科学思维素养水平3层次的培养，即在熟悉的问题情境中选用恰当模型来解决简单的物理问题，用模型结论来分析常见的问题，进一步通过推理获得结论、解释结论[1]。

（三）训练三

如图5，质量m的小球通过长L的轻质细杆与滑块上的光滑轴O连接，质量M的滑块套在光滑的水平轨道上，小球和轻杆可在竖直平面内绕O轴自由转动，开始轻杆处于水平状态。给小球m一个竖直向上的初速度，试求小球起始位置与小球击中滑块右侧轨道位置点间的距离。

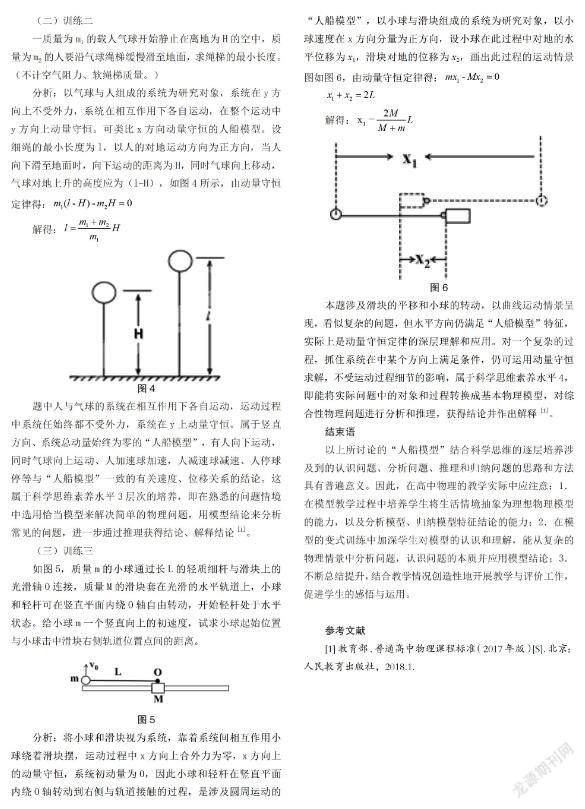
分析：将小球和滑块视为系统，靠着系统间相互作用小球绕着滑块摆，运动过程中x方向上合外力为零，x方向上的动量守恒，系统初动量为0，因此小球和轻杆在竖直平面内绕O轴转动到右侧与轨道接触的过程，是涉及圆周运动的“人船模型”，以小球与滑块组成的系统为研究对象，以小球速度在x方向分量为正方向，设小球在此过程中对地的水平位移为x1，滑块对地的位移为x2，画出此过程的运动情景图如图6，由动量守恒定律得：

解得：

本题涉及滑块的平移和小球的转动，以曲线运动情景呈现，看似复杂的问题，但水平方向仍满足“人船模型”特征，实际上是动量守恒定律的深层理解和应用。对一个复杂的过程，抓住系统在中某个方向上满足条件，仍可运用动量守恒求解，不受运动过程细节的影响，属于科学思维素养水平4，即能将实际问题中的对象和过程转换成基本物理模型，对综合性物理问题进行分析和推理，获得结论并作出解释[1]。

结束语

以上所讨论的“人船模型”结合科学思维的逐层培养涉及到的认识问题、分析问题、推理和归纳问题的思路和方法具有普遍意义。因此，在高中物理的教学实际中应注意：1.在模型教学过程中培养学生将生活情境抽象为理想物理模型的能力，以及分析模型、归纳模型特征结论的能力;2.在模型的变式训练中加深学生对模型的认识和理解，能从复杂的物理情景中分析问题，认识问题的本质并应用模型结论;3.不断总结提升，结合教学情况创造性地开展教学与评价工作，促进学生的感悟与运用。

参考文献

[1]教育部.普通高中物理课程标准（2017年版）[S].北京：人民教育出版社，2018.1.