变式训练教学模式在高中数学解题中的应用分析

张固喜

摘 要：变式训练教学模式主要培养学生灵活运用数学知识能力，从多角度开发学生大脑，激发学生潜能，提高学生参与数学学习的积极性，培养学生发现、感悟、归纳数学知识，解决数学问题的能力。本文简要阐述了变式训练教学模式在高中数学解题中应用方法。

关键词：变式训练；教学模式；高中数学解题

中图分类号：G633.61 文献标识码：A 收稿日期：2015-12-14

一、高中数学教学采用变式训练教学模式的意义

1.启发学生的归纳、分析、概括能力

受传统教学模式的影响，数学教学活动中学生做题思维越来越被固化，很多学生走“捷径”，在原有的归纳总结中采用“套公式”的学习方式，湮灭了数学的魅力，从而无法真正理解数学内涵。变式训练教学模式，有利于学生联想、转化、推理思维能力的拓展，通过将已知问题运用到未知问题解题方面上，有利于学生创新思维能力的培养，可培养学生的创新能力和创新精神。使用变式训练教学模式灵活改变知识点表达方式，拓展学生整体思维水平，让学生学会做题的同时，其思维也得到训练，学生成绩自然而然得到提高。例如学习高中数学有理指数幂的运算性质时，可以归纳出指数幂的运算法则，包括：①an·am=an+m；②（am）n=am·n ；③（a·b）m=am·bm。通过多种变式，从各个方面直观地表达概念的定义，使学生对概念有更深的理解，对概念当中的本质东西有清晰的认识，从而提高学生学习效率，促使他们在有限学习时间里实现学习效益最大化。

2.培养学生多向变通的思维能力

数学思维的培养还包括定理、推理和性质应用能力，理解定理、推理和性质之间的联系有利于学生整体数学成绩的提高。例如，在解决平面的基本性质及运用问题时，可设计题目：四边形ABEF和ABCD都是直角梯形，如图1所示，∠BAD=∠FAB=90°，BC=—AD，BE=—FA，G、H分别是FA、FD的中点。

问题：C、D、F、E四点是否共面？ 为什么？

这道题目有两种解题思路。第一种方法：证明D点在EF、CH确定的平面内。第二种方法：如图2所示，延长FE、DC分别与AB交于M，M'，可以证明M与M'重合，从而证明FE与DC相交。

第一种解法使用基本思路证明四点共面。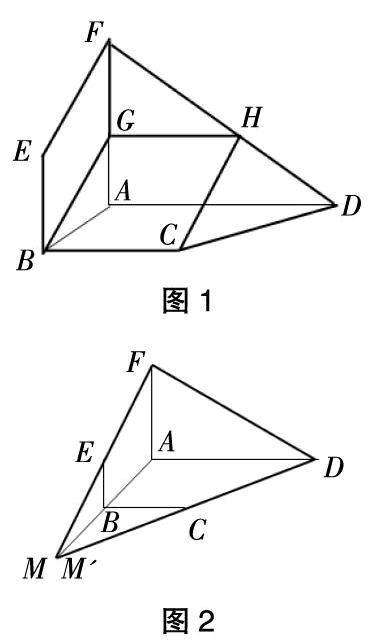

具体解法：由于BE=—AF，G是FA的中点，可以得到BE=FG，所以四边形BEFG是平行四边形，所以EF平行BG。由题目BG平行CH可以得到EF平行CH，EF与CH共面；又因为D属于FH，所以C、D、F、E四点共面。

第二种方法通过作图，使用变通式思维拓展学生解决问题能力。

具体解题方法如图2所示，通过延长FE，DC分别与AB交于点M，M'，因为BE=—AF，所以B是MA的中点；又因为BC=—AD，所以B为 A之中点，所以M与M'重合，FE与DC相交于点M（M'），所以C、D、E、F四点共面。

二、应用变式训练教学模式应注意的问题

变式训练教学在高中数学教学当中虽然有很多好处，但是它也有变式教学模式难以取代的地方，并不是在任何方面变式教学模式都能取得良好教学效果。只有通过合理运用变式教学模式，才能达到事半功倍的效果。变式训练教学模式要注重对思维的培养，达到举一反三的效果；而不能仅仅使用题海战术巩固思维模式。题海战术运用在基础知识的学习当中能够取得较好的效果，但是在变式训练教学活动中，却会让学生的思维在另一方面变得僵化，缺少灵机应变的解题能力。变式训练教学模式要穿插在基础教学内容当中，在学生掌握基础知识之后，使用变式训练教学模式加深学生对基础知识的理解，从另一个思维角度对变式训练教学进行自我反思，以完善数学知识体系。

参考文献：

[1]徐丽平.高中数学解题中变式训练教学模式的应用[J].考试周刊，2014，（2）：55.

[2]金瑶丹.变式教学模式在初中数学教学中的应用[J].语数外学习（初中版下旬刊），2014，（6）：24.