基于改进的TOPSIS-CV法的边坡稳定性分析

摘要：为提高边坡稳定性评价结果的准确性，应用TOPSIS法，并将垂面距离代替欧氏距离的正交投影法与之结合，采用变异系数法确定指标客观权重，提出一种改进的TOPSIS-CV法。从边坡几何参数、岩体强度参数及外部情况等3个方面综合考虑影响边坡稳定性的7个评价指标，建立边坡稳定性的评价指标体系，将改进的TOPSIS-CV模型应用于某露天矿边坡的稳定性综合评价中。研究结果表明：采用垂面距离代替欧氏距离，贴近度更加容易区分，边坡稳定性评价结果准确率达90 %;与传统的TOPSIS法相比，改进的TOPSIS-CV法计算结果更为精确，更加容易对边坡稳定性进行综合评判;改进的TOPSIS-CV法具有良好的工程应用价值。

关键词：露天开采;边坡稳定性;改进的TOPSIS-CV法;垂面距离;正交投影法

中图分类号：TD854+.6          文章编号：1001-1277（2021）05-0035-05

文献标志码：A   doi：10.11792/hj20210507

引 言

边坡作为露天矿的一个重要组成部分，其稳定与否直接影响露天矿的安全生产和经济效益。然而，在一些复杂地质条件、气候条件及人为活动等作用下，边坡的稳定性变得十分复杂，在不良因素，如降水、爆破等影响下，边坡稳定性受到严重威胁，一旦边坡发生失稳破坏，不仅会造成人员伤亡、财产损失，对周边环境也将产生较大的破坏，而且也会严重影响露天矿的正常生产作业。因此，开展露天矿边坡稳定性研究非常有必要。

近年来，国内外学者们针对边坡稳定性进行了大量的分析研究。程杰等[1]采用FAHP模型对某露天矿的边坡稳定性进行了评定，同时运用模糊隶属函数计算了10个边坡影响因素的隶属度，确定了各参数权重，评价结果与工程实际相符。仲静文等[2]采用粒子群优化K-Means聚类算法，克服了常规K-Means算法容易陷入局部最优的不足，将该方法应用于三峡库区36个边坡工程中，得到了更为可靠的结果。陈昊等[3]、何奕良等[4]分别采用博弈论、德尔菲结合理想点法对边坡稳定性进行了准确的评价。另外，单一的模糊综合评价方法在边坡稳定性评价中也得到了广泛的应用[5-8]，且评价结果相对来说较为可靠。而黄永刚等[9]将BP神经网络及模糊综合评价法在边坡稳定性评价中的结果进行了对比，结果表明神经网络的评判结果具有更高的精度。

TOPSIS法（理想点法）是一种优劣度（等级）综合评价方法，该方法在矿井通风评价[10]、采矿方法优选[11]及岩爆预测[12]等工程中获得了较好的应用，解决了许多工程评价和优选的问题。但是，传统的TOPSIS法均以欧氏距离作为计算方案到正理想解的贴近度，评价结果存在一定的模糊性及不确定性。因此，本文用评价方案指标的垂面距离替代传统的欧氏距离，以正交投影法对TOPSIS法进行优化，同时，针对层次分析法、专家打分法等计算权重时主观性较大的问题，利用客观权重赋值的变异系数法（CV）进行评价指标权重的确定。将改进的TOPSIS-CV模型应用于某露天矿边坡稳定性评价中，为解决边坡稳定性问题提供了新的思路。

1 变异系数法确定权重

变异系数法（CV）是计算客观权重的一种方法，其最大的优点是评价指标的权重计算完全依靠指标数据，有效地对主观因素的影响进行了规避[13]。该算法的核心在于：将评价指标的变异度作为确定指标权重的依据，指标权重随方案数据不断发生变化。因此，CV法是一种客观、动态的赋权方法。

对于评价指标集H={h1，h2，…，hj，…，hn}（j=1，2，…，n），当某一特定指标hj在待评价方案G={g1，g2，…，gi，…，gm}中的波动值较大时，那么认定该指标对方案优劣度的影响程度较大;反之，则认定hj对方案优劣度的影响较小。当hj对其他待评价方案优劣度不产生影响时，则表示该指标对评价结果无影响。因此，指标的变化范围可以确定指标权重，具体如下：

1）建立评价指标决策矩阵（A）：

由式（5）确定每个指标的权重，且∑nj=1ωj=1。

2 改进的TOPSIS-CV法评价模型

2.1 基本原理

HWANG等最初提出了TOPSIS法，它是解决多目标决策的一种可靠方法。在工程实际中，TOPSIS法设定了评价方案的一个正理想解（最优方案）及负理想解（最差方案），将某一待评价方案到正、负理想解的欧氏距离作为方案的贴近度，然后将贴近度从高到低排序，将距离正理想解最近、负理想解最远作为最优方案;反之，则为最差方案。

传统TOPSIS法对指标与正理想解的欧氏距离进行计算，作为获得贴近度的依据，这样一来，致使在多个待评价方案中，方案与正、负理想解的贴近度可能差异很小。因此，计算结果對各方案优劣度的判断存在模糊性和不确定性。例如：对于含有2个评价指标x1和x2的方案，假设存在4个待评价方案A（x1A，x2A）、B（x1B，x2B）、C（x1C，x2C）和D（x1D，x2D）的样本点，E（x+1，x+2）、F（x-1，x-2）分别为评价方案的正、负理想解，如图1所示，AB、CD均为EF的垂线，如果采用传统TOPSIS法计算，评价方案到正理想解的贴近度为：

E+i=diFdiE+diF（6）

式中：E+i为正理想解贴近度;diE和diF分别为方案到正、负理想解的欧氏距离。

由几何学可知，E+B>E+A，E+D>E+C，方案B、D分别优于方案A、C，但实际上，方案B相较方案A更贴近正理想解，同时又更贴近负理想解，这就使得计算结果存在一定的矛盾。而由于AB为EF的垂线，方案A、B到正、负理想解的贴近度是相同的，二者具有相同的排序。为了解决上述问题，本文以垂面距离代替欧氏距离，对TOPSIS法进行改进，从而克服欧氏距离在反映方案排序方面的不足[14]。

采用正交投影法，计算方案与正理想解的垂面距离如图1所示。E、F点分别为正、负理想解，以EF为法线作垂面α、β，α、β之间的距离即为垂面距离。垂面α、β上点A和D在EF上的投影为O和P，因此方案A和方案D的垂面距离即为点O和点P之间的欧氏距离，即垂面α、垂面β之间的距离。

根据垂面距离的概念，α面上方案A和方案B到正理想解E的垂面距离相等，为dOE。因此，认为方案A和方案B具有相同的贴近度，同理，方案C和方案D 也具有相同的贴近度，它们之间的排序是一致的。

2.2 边坡评价模型建立

1）综合已有的研究成果[3]，边坡的稳定性影响因素包括边坡几何参数、岩土体强度参数及外部情况等几种。本文参考文献[3]，以3大类9个子因素为定性定量评价指标，建立改进的TOPSIS-CV法边坡评价指标体系，如图2所示。

2）采用变异系数法确定各指标权重。计算指标权重向量（ω）：

ω=（ω1，ω2，ω3，ω4，ω5，ω6，ω7，ω8，ω9）  （7）

3）建立标准化决策矩阵。为了消除指标之间不同量纲的影响，对指标的特征值矩阵（O）进行标准化处理，得到标准化决策矩阵（P）。

式中：J1为效益型指标集;J2为成本型指标集。

为简化计算过程，将正理想解进行平移，使其平移到原点，令平移矩阵R=（rij）m×n，满足rij=qij-Q+j。因此，经过上述处理后，Q+j=0，Q-j=rkj，且rkj≥rij，k∈[1，m]。

6）计算待评价方案的垂面距离。在图1中，B、C、E、F的向量分别为b，c，e，f，则B和C的垂面距离（dBC）为：

dBC=（b-c）·（e-f）‖e-f‖（13）

式中：‖e-f‖为2范数，即E和F之间的欧氏距离。

因此，只需要计算（b-c）·（e-f），方案i到正理想解的垂面距离为：

di=（u-v）（u-Ri）=Q-Ri=∑nj=1Q-jrij（14）

式中：u、v分别为平移后的正、负理想解;Ri为平移矩阵（R）的第i行向量。

7）计算待评价方案到正、负理想解的垂面距离（di）后，根据di进行排序，di越小，表示该方案越接近正理想解，方案越好;反之，方案越差。

3 工程应用

河南某钼矿规模为特大型，目前已探明钼矿石量达到350 236.8 kt，金属量为396 191.5 t，Mo平均品位0.113 %。该矿区矿体厚大，品位较高，表土覆盖层薄，适合于大规模的露天开采。其边坡参数为：台阶高度15～35 m，共分为40个台阶，坡面角度为25°～45°，开挖台阶数为1～5个。矿区的节理裂隙较发育，但总体规模较小，且节理之间一般未发生连通，对地层的完整性和连续性影响很小，其区域内包括一系列走向北东或近东西的断裂带和褶皱，且大小不一。其边坡岩石主要由变质泥质砂岩、变质砂质泥岩和变质砂岩等构成。根据该露天矿边坡设计参数及岩性条件，其边坡稳定性受设计参数的影响较大，为了减少和预防边坡失稳造成的生产事故，本文拟针对该露天矿开采过程中的边坡稳定性进行合理的评价。

该露天矿边坡稳定性评价指标如图2所示，其稳定性等级相应地被划分为稳定（Ⅰ）、基本稳定（Ⅱ）、不稳定（Ⅲ）和极不稳定（Ⅳ）4个等级，对应的分级标准[4]如表1所示。

3.1 边坡稳定性待评价方案

根据该露天矿生产报告所提供的10个边坡原始数据指标，作为10个待评价方案，如表2所示。

3.2 变异系数法计算指标权重

1）按照式（1）～（5），首先计算出每项指标的平均值，分别为：h1=34.60、h2=20.70、h3=26.00、h4=18.54、h5=26.04、h6=15.70、h7=16.47、h8=2.30、h9=144.55。

2）計算每项指标的均方差，分别为：σ1=4.94、σ2=5.48、σ3=0.49、σ4=0.90、σ5=13.00、σ6=7.52、

3）计算每项指标的变异系数，分别为：δ1=0.143、δ2=0.265、δ3=0.188、δ4=0.048、δ5=0.500、δ6=0.479、δ7=0.213、δ8=0.340、δ9=0.487。

4）确定指标权重向量：ω=（0.054，0.099，0.071，0.018，0.188，0.180，0.080，0.128，0.183）。

3.3 待评价方案垂面距离

1）根据式（7）、式（8）对由表2所组成的决策矩阵进行归一化处理，其中，为了计算各指标与各等级的贴近度，最大值与最小值由表1中各指标决定，由此建立标准化的决策矩阵（P）：

将矩阵P中每项指标与其对应的权重相乘，得到加权决策矩阵（Q）：

在表1的指标中，除内聚力、内摩擦角为效益型指标，其余全为成本型指标。因此，经过归一化及加权后Ⅰ～Ⅳ等级方案的正、负理想解为：

将各等级中正理想解移至坐标原点，得到平移矩阵R，以等级Ⅰ为例，其平移矩阵RⅠ为：

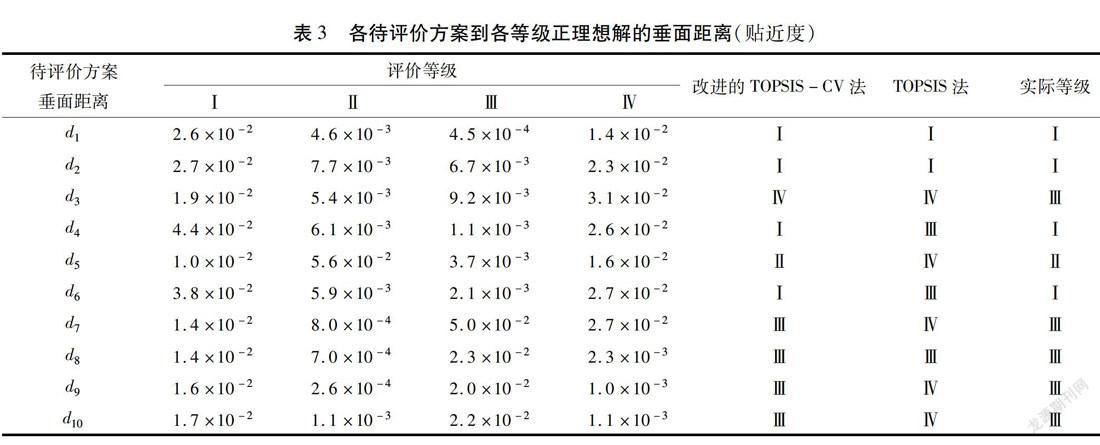
根据式（14）计算得出10个方案到4个等级正理想解的垂面距离，如表3所示。

3.4 评价结果分析

由表3评价结果可知，采用改进的TOPSIS-CV法计算得到的评价结果的准确度较传统TOPSIS法计算的准确度大幅度提升，除了待评价方案3与实际等级存在差异外，其余各方案评价结果与实际结果一致，评价准确率达到了90 %。与传统的TOPSIS法相比，改进的TOPSIS-CV法更加能对各方案的垂面距离（贴近度）进行区分，凸显出该评价模型的准确性与可靠性，能够较为简单、准确地对边坡稳定性等级进行判断。

4 结 论

1）建立了边坡稳定性改进的TOPSIS-CV法评价模型，通过将传统TOPSIS法欧氏距离替换成垂面距离的方法，对贴近度排序计算方法进行了优化，改进了传统TOPSIS法存在排序模糊不清的不足，使得评价结果更加合理、准确。

2）利用变异系数法计算评价指标权重，有效地避免了主观因素对评价指标权重的影响，充分对评价指标的实际数据进行挖掘，获得了更加符合客观实际的指标权重。

3）针对该特大型钼矿露天边坡稳定性，采用改进的TOPSIS-CV法评价模型对其进行评价，计算出了各待评价方案的垂面距离，除方案3与实际结果存在一些差异外，其余方案评价结果均与实际结果一致，其评价准确率达90 %，获得了良好的应用效果，具有较好的工程应用价值。

[参考文献]

[1] 程杰，吴贤振，王庆，等.基于FAHP模型的边坡稳定性评价[J].矿业研究与开发，2019，39（12）：46-50.

[2] 仲静文，郝利朋，周健.基于PSO优化K-Means算法的边坡安全等级评价研究[J].水利规划与设计，2020（3）：94-97.

[3] 陈昊，张楚怡，魏荣誉.基于博弈论组合赋权与理想点法的边坡稳定性分级评价[J].内蒙古科技与经济，2020（10）：105-108.

[4] 何奕良，李牟.基于德尔菲-理想点法的露天矿边坡稳定性分析[J].采矿技术，2020，20（2）：56-59.

[5] 温世亿，李建林，杨学堂，等.卸荷高边坡稳定性分析的多级模糊综合评判[J].岩土力学，2006，27（11）：2 041-2 044.

[6] 陈云超，杨平庆.模糊综合评判在山区公路边坡稳定性分析中的应用[J].水利与建筑工程学报，2018，16（6）：202-206，229.

[7] 洪海春，徐卫亚，叶明亮.基于模糊综合评判的边坡稳定性分析[J].河海大学学报（自然科学版），2005，33（5）：557-562.

[8] 刘华丽，卢厚清，李宏伟，等.模糊综合评判法在边坡稳定性分析中的应用[J].解放军理工大学学报（自然科学版），2013，14（1）：84-88.

[9] 黄永刚，张学焱，李雪珍，等.神经网络和模糊综合评判在边坡稳定性分析中的应用比较[J].有色金属科学与工程，2016，7（3）：94-99.

[10] 吴立云，杨玉忠，张强.矿井通风系统评价的TOPSIS方法[J].煤炭学报，2007，32（4）：407-410.

[11] 赵国彦，唐洋，刘志祥，等.基于改进的AHP-TOPSIS评判模型的盛大铁矿采矿方法优选[J].科技导报，2013，32（3）：25-28.

[12] 龚剑，胡乃联，崔翔.基于AHP-TOPSIS评判模型的岩爆倾向性预测[J].岩石力学与工程学报，2014，33（7）：1 142-1 148.

[13] 刘培德，关忠良.属性权重未知的连续风险型多属性决策研究[J].系统工程与电子技术，2009，31（9）：2 133-2 136.

[14] 肖淳，邵东国，杨丰顺.基于改进TOPSIS法的流域初始水权分配模型[J].武汉大学学报（工学版），2012，45（3）：329-334.

Slope stability analysis based on improved TOPSIS-CV method

Luo Yueming

（Fujian Geotechnical Engineering Investigation and Research Institute Co.，Ltd.）

Abstract：In order to improve the accuracy of the slope stability evaluation results，the TOPSIS method is applied combined with the orthogonal projection method with Euclidean distance replaced by vertical distance，the variation coefficient method is used to determine the objective weight of the index，and an improved TOPSIS-CV method is proposed.7 evaluation indexes affecting slope stability are comprehensively considered from 3 aspects：slope geometric parameters，rock mass strength parameters and external conditions，the slope stability evaluation index system is established，and the improved TOPSIS-CV model is applied to the comprehensive evaluation of slope stability of an open-pit mine.The research results show that using the vertical distance instead of the Euclidean distance，the paste progress is easier to distinguish，and the accuracy of the slope stability evaluation results is 90 %，compared with the traditional TOPSIS method，the improved TOPSIS-CV method is more accurate and can more easily comprehensively evaluate the slope stability，the improved TOPSIS-CV method has good engineering application value.

Keywords：open-pit mining;slope stability;improved TOPSIS-CV method;vertical distance;orthogonal projection method

收稿日期：2020-11-25; 修回日期：2020-12-08

作者簡介：罗月明（1978—），男，福建三明人，高级工程师，从事岩土工程设计、地质灾害设计等方面的研究工作;福州市闽侯县上街镇科技东路1号三层，福建岩土工程勘察研究院有限公司，350001;E-mail：42037965@qq.com