基于PCA—GRNN神经网络的露天矿边坡稳定性分析

闫守志　郭绍征　陈勇智　赵建强　倪泽雨

摘 要：露天矿边坡稳定性分析是一个复杂的非线性、不确定的动态系统，各因素之间具有一定的相关性。首次应用主成分与GRNN神经网络结合的原理和方法，建立了边坡稳定性评价模型，能定量得出各主成分对边坡稳定性的影响程度。利用PCA-GRNN神经网络评价模型对边坡安全系数进行了预测，并与真实值进行了对比分析，得出了PCA-GRNN方法评价精度较高、相对误差较小。由此可见，该模型在边坡稳定性的分析中具有较高的可行性和适用性。

关键词：边坡稳定性；主成分分析；GRNN神经网络；特征根

中图分类号：TD854.6 文献标识码：A DOI：10.15913/j.cnki.kjycx.2016.16.013

露天矿边坡稳定性分析是工程界和学术界关注的重要课题，但各因素间的交互作用在单因素分析的方法中已被忽略，无法很好地符合实际情况。国内外使用较为广泛的边坡稳定性分析方法主要有数值分析法、极限平衡法等。这些方法都需综合考虑影响边坡稳定的主要因素，其过程比较复杂，计算烦琐，无法准确地描述边坡的非线性特征。由于计算机技术的不断进步，关于边坡稳定性评价的方法得到了的改进，一些复合评价方法也被逐渐应用到了边坡稳定性的分析中。冯夏庭等人提出了边坡稳定性的神经网络估计方法。 主成分分析方法应用已较为成熟，但运用主成分对边坡稳定性的研究较为缺乏。

1 主成分分析法的基本思想

在对实际问题研究的过程中，一般情况都是关于n个样本，每个样本包含p个随机变量的问题，数学上的处理方式为将原始的p个变量作线性组合。作为新的变量，设p个原始变量为x1，x2，…，xp，对应的新的变量（主成分）为y1，y2，…，yp.

主成分方差贡献率为某个特征根占总特征的根比例。设特征根为λ，则第i个主成分所对应的方差贡献率为：

特征值累计贡献率一般要求在75%～85%，其中，特征值即主成分的个数小于5或6.主成分分析是将原来多个变量化为少数几个综合指标的一种统计分析方法。从数学角度看，这是一种降维处理技术。假定有n个地理样本，每个样本共有p个变量描述，这样就构成了一个n×p阶的数据矩阵。

2 GRNN神经网络的基本思想

广义回归线性网络GRNN的主要优点在于学习快速，是一种基于非线性回归理论的前馈式神经网络模型。当样本数量非常大时，GRNN神经网络能实现快速逼近，处理实时环境中的稀疏数据时非常有效。目前，该神经网络在系统辨识和预测控制等方面得到了应用。

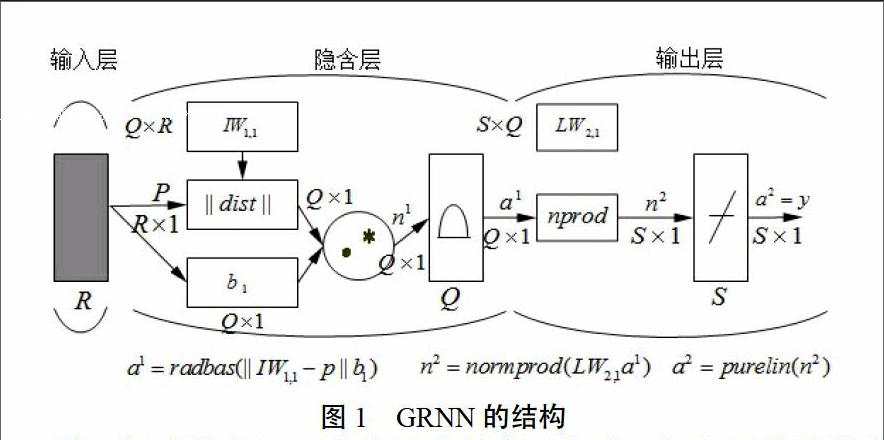
GRNN的结构如图1所示。

其一般由输入层、隐含层和输出层组成。输入层能将样本变量传递到隐含层，将不参与真实运算。隐含层所含神经元个数是训练集样本数，其权值为欧氏距离函数（ ），作用是为计算网络输入与第一层的权值IW1，1间的距离，b1为隐含层阀值。使用径向基函数作为隐含层传递函数，一般采用高斯函数为传递函数。网络中第三层为线性输出层，其权函数为规范化点积权函数（用nprod表示），计算网络的向量为n2，其每个元素就是向量a1和权值矩阵LW2，1每行元素的点积再除以向量a1的各元素之和得到的，并将结果n2提供给线性传递函数a2=purelin（n2），计算网络输出。

3 边坡影响因素间的相关性分析

本文所选取岩土体的重度γ、岩土体的黏聚力c、内摩擦角f、边坡的坡角α，边坡的高度H以及孔隙压力μ作为影响边坡稳定的主要因素。从大量参考文献得出边坡稳定性评价的输出因素为边坡安全系数。

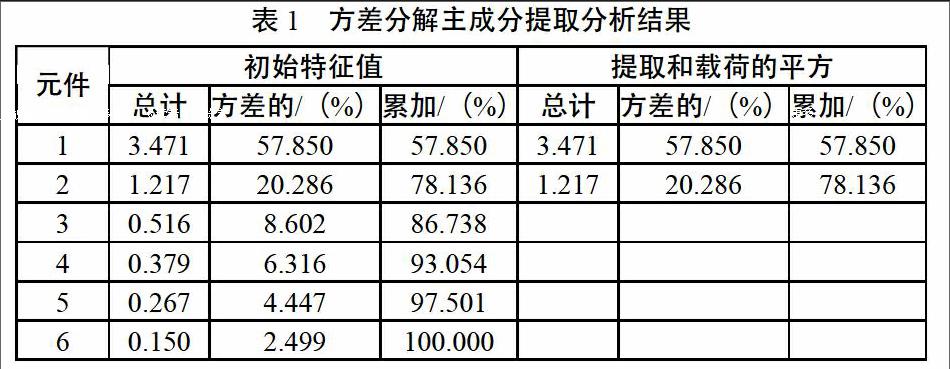
由于各指标对应的变量因子所采取的单位标准不一样，因此，各变量之间无法直接比较，对数据标准化处理需要在进行主成分分析前进行。其中，SPSS主要使用z-score标准化法，可将数据统一映射到[-1，1]区间上。方差分解主成分提取分析结果如表1所示。

表1中，利用SPSS提取出2个主成分，且方差累计贡献率大于75%，所以，提取的主成分有效。近一步借助其求得主成分因子的载荷矩阵，具体如表2所示。

由于利用SPSS进行主成分分析时，无法直接得出主成分的系数。表2中主成分载荷矩阵并不是主成分的特征向量，其系数的准确求法则为：各个主成分载荷除以表1中各个主成分所对应特征值的算术平方根。根据主成分分析模型和因子载荷，可以得到提取的2个主成分与原先6个指标变量之间的线性组合，表达式如下：

4 PCA-GRNN预测数值实例

由于输入数据具有一定相关性和输入数据过多，所以，本文将主成分分析法与GRNN神经网络相结合，构建了优选模型，并对边坡安全状态进行有效了分析。将18组数据作为训练样本子集，预测样本子集的11组边坡数据。该案例分析中的学习速率设为0.01，最大迭代次数为2 000，误差性能目标为0.000 001.分别运用两种算法对边坡的安全性进行了比较分析，结果如表3所示。

通过对两种预测方法所预测结果的平均值、最小值以及最大值的比较可以得出，PCA-GRNN算法比PCA-BP算法的预测结果更为准确。由此额空间，该方法在边坡稳定性分析上较为有效、合理。

两种方法的预测值与实际测量值之间的误差关系如图2所示。

由此可见，利用PCA-GRNN模型进行评价比利用PCA-BP得出的预测值精度更高、相对误差更小。该模型在边坡稳定性分析中具有较好的可行性和适用性。

5 结论

以PCA-GRNN方法描述了分类结果与样本值两者间的映射关系，给出了具体的概率累计表达式与模型建立的方法，并通过对某一工程实例的验证得出，采用PCA-GRNN模型描述边坡稳定性分类指标与稳定性之间的经验关系，其建模方法简单，易于实现。与BP神经网络相比，GRNN网络优势在于训练不需要迭代、隐含层所含神经元个数由训练样本可自适应确定，避免了BP神经网络在迭代中的权值修改，且对接近于局部神经元特征的输入具有很强的吸引力等。

参考文献

[1]胡敏萍.极限平衡法和有限单元法分析复杂边坡的稳定性[D].杭州：浙江大学，2004.

[2]郭子仪，范振华，朱云升，等.边坡稳定性分析中的有限元极限平衡法[J].武汉理工大学学报（交通科学与工程版）， 2014，38（01）.

[3]冯夏庭，王泳嘉.边坡稳定性的神经网络估计[J].工程地质学报，1995，3（04）.

[4]熊海丰.基于人工神经网络技术的边坡稳定性评价研究[D].武汉：武汉理工大学，2003（05）.

[5]张表志.基于主成分分析的大型弃土场边坡稳定性敏感因素分析[J].公路交通科技（应用技术版），2013（07）.

[6]谷琼，蔡之华，朱莉.基于PCA-GEP算法的边坡稳定性预测[J].岩土力学，2009，30（03）.

[7]张文霖.主成分分析在SPSS中的操作应用[J].市场研究，2005（12）.

[8]张绍红.概率神经网络技术在地震岩性反演中应用[J].辽宁工程技术大学学报，2007（26）.

[9]兰海涛，李谦，韩春雨.基于广义回归神经网络的边坡稳定性评价[J].岩土力学，2009，30（11）.

[10]陈建宏，郑荣凯，陈浩.基于PCA和BP神经网络边坡稳定性分析[J].中国安全生产科技术，2014（05）.

〔编辑：张思楠〕