膜片弹簧力学性能有限元分析

廖升友 杨有春

摘要：为分析具有对称结构的膜片弹簧的载荷特性曲线，利用ABAQUS软件建立了膜片弹簧单分离指结构的有限元模型，通过施加位移载荷模拟了膜片弹簧的压紧行程和分离行程，得到膜片弹簧的载荷-位移非线性特性曲线，并与Almen-Laszlo公式计算结果对比。结果显示，有限元计算得到特性曲线与理论公式计算结果趋势接近，验证了有限元模型的准确性。

关键词：膜片弹簧;有限元分析;载荷-位移曲线;非线性

中图分类号：U463.211                                  文献标识码：A                                  文章编号：1674-957X（2021）05-0044-02

0  引言

膜片彈簧离合器具有非线性弹性特性好、高速工作时压紧力变化小，压紧力分布均匀，耐高温寿命长等优点被广泛地应用于轿车、客车、卡车等车辆中。本文建立了单分离指结构的模片弹簧有限元分析模型，通过施加位移载荷模拟膜片弹簧工作过程的压紧行程和分离行程，得到膜片弹簧的负荷特性曲线以及分离指的应力分布。

1  膜片弹簧结构

膜片弹簧的载荷-变形非线性特性是膜片弹簧非常关键的性能，通常在产品设计初分析时采用美国工程师Almen和Laszlo所提出的Almen-Laszlo公式（简称A-L公式）预测膜片弹簧的载荷-变形特性曲线[1，2]：A-L公式形式简单，计算方便，但A-L公式计算结果与测试曲线仍存在较大误差[3，4]。随着三维有限元仿真技术发展，采用有限元计算的载荷变形曲线比A-L公公式计算结果更接近实测结果[4-7]。膜片弹簧因与压盘、分离指、支撑圈、分离轴之间存在摩擦和接触，膜片弹簧本身载荷-位移非线性特性决定了膜片弹簧仿真分析存在高度非线性，建立完整膜片弹簧进行有限元仿真分析通常非常耗时。针对膜片弹簧通常是周向对称结构特点，为减少计算量。

2  有限元模型

2.1 模型的建立

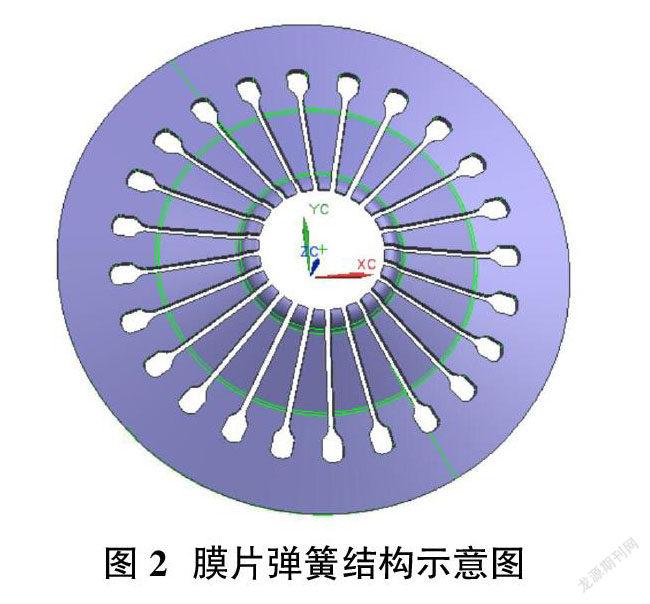
图2为某企业生产广泛应用于卡车的膜片离合器，该膜片弹簧共24指，每指间隔15°。因为每指的结构完全一样，因此在有限元分析时取其中一个分离指进行分析，如图3所示。

用UG软件建立膜片弹簧的三维模型，并选取其中的一个分离指导入Hypermesh前处理软件进行网格划分，并细化与分离指有接触关系区域、分离指圆角以及可能出现大应力区域的网格。然后将网格文件导入Abaqus有限元分析软件进行建模、施加载荷、约束边界、进行求解和结果分析。分离指选用10节点二阶四面体修正单元C3D10M，弹性模量取202GPa，泊松比0.3;与膜片弹簧分离指接触的支撑圈、压盘、分离轴等的零件使用刚性面模拟，这样既可以减小有限元模型规模，也有助于提高有限元计算的收敛性。整个有限元模型共包含77440个单元，127495个节点。图4为在Abaqus软件中建立的有限元模型。初始时刻分离指与膜片弹簧支撑圈I、膜片弹簧支撑圈II、压盘、分离轴处于接触状态。

2.2 边界条件

在膜片弹簧中心线上建立圆柱坐标系，Z向与膜片弹簧中心线重合，R向径向与膜片弹簧径向相同，θ为周向。在膜片弹簧中心线上分别为分离轴、支撑圈Ⅰ、支撑圈Ⅱ、压盘等刚性面建立RP耦合点，耦合点与对应的刚性面具有相同的Z向的高度，如图5所示;建立耦合点与刚性面之间的刚性约束，通过约束耦合点的Z自由度驱动各刚性面的Z向运动，模拟膜片弹簧压紧和分离过程;在分离指与分离轴、弹簧支撑圈、压盘之间的接触面上建立接触副，摩擦系数取0.15;约束分离指切面的θ向自由度。

2.3 载荷施加与求解

根据膜片弹簧离合器工作原理，在压盘未安装到飞轮上时，膜片弹簧是自由的;当压盘与飞轮装配好后，膜片弹簧受压，膜片弹簧对压盘产生压紧力使得离合器处于接合状态;当离合器分离时，分离轴推动膜片弹簧使离合器分离。因此计算工况包含压紧工况和分离工况。通过位移载荷施加到对应的RP参考点上模拟膜片弹簧的工作过程。

压紧工况：压盘往分离轴方向位移5.5mm;

分离工况：保持压紧位置不变，分离轴向压盘方向位移12mm。

上述两个分析工况在计算时分离指的几何结构均发生了大变形，因此在有限元计算时需要考虑几何非线性的影响，采用Full Newton方法求解。

3  计算结果与分析

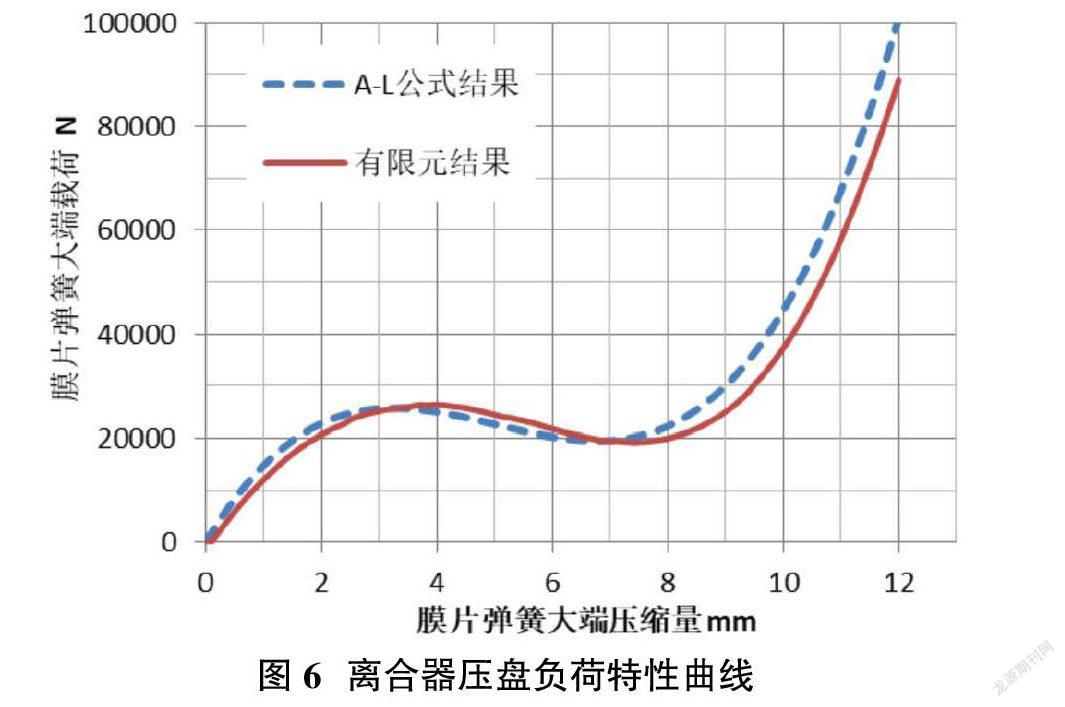
在Abaqus软件后处理模块提取RP耦合点的力与位移结果，得到单个分离指的载荷-位移特性曲线。由于该膜片弹簧有24个分离指，因此将单个分离指的载荷乘以24后，即可得到整个膜片弹簧的载荷-位移特性曲线，如图6红线所示。

图6中的蓝线是利用膜片弹簧的几何参数（如表1所示），根据A-L公式计算得到的载荷-位移结果。从图6中可见有限元模型计算的拐点位置及对应的载荷幅值与A-L公式计算的趋势接近，这说明了有限元模型的准确性。

因有限元模型考虑了膜片弹簧与分离轴、支撑圈及压盘之间的接触和摩擦，同时有限元仿真可模拟膜片弹簧工作过程中与支撑面接触点的变化，这是A-L公式无法考虑的[3-7]。因此有限元计算结果更接近试验值。

4  结论

利用膜片弹簧的周向对称型，选取1个分离指模型，并将分离指、支撑圈和压盘等零部件简化为刚性面建立膜片弹簧有限元分析模型。结果显示通过该有限元分析得到的离合器载荷-位移非线性特性曲线与使用Almen-Laszlo公式计算结果的拐点位置、载荷幅值接近，验证了有限元模型的准确性。因有限元模型考虑了膜片弹簧与分离轴、支撑圈、压盘等零件的接触和摩擦关系，同时可考虑膜片弹簧与支撑面接触点的变化，因此有限元计算得到的结果更准确。

参考文献：

[1]林恩，桂良进，范子杰.膜片弹簧力学特性有限元分析[J].汽车工程，2010，32（10）：892-896.

[2]薄小斌，张晓东，张瑞亮，郭亚敏.分离指加强筋对膜片弹簧性能影响的仿真研究[J].中国农机化学报，2016（4）：49-53.

[3]张铁山.膜片弹簧大端载荷与变形特性计算方法的误差分析[J].汽车技术，2009（1）：26-29.

[4]赵毅斌，刘夫云，胡汝凯，余汉红.分离指结构对膜片弹簧载荷变形特性的影响[J].机械设计与制造，2020（5）：138-141.

[5]杨橙.汽车离合器膜片弹簧的有限元分析[J].机电技术，2005（1）：37-38.

[6]王博.基于有限元法的膜片弹簧特性曲线仿真分析[J].拖拉机与农用运输车，2007，34（1）：90-92.

[7]袁旦，李芳，郑方赐.基于非线性有限元法的膜片弹簧特性曲线计算[J].浙江工业大学学报，2009（3）：350-354.