“寻规、导据、立本”再谈“数形结合”

赵梅

【摘要】教师针对新教授内容的巧妙设计，是对培养学生的思维能力的训练，以及激发学生学习的能动性、自主性及创设和谐的学习氛围，都有着十分重要的意义。

【关键词】数形结合;课堂教学;解决问题

二次函数是初中数学重要的内容之一，对此，教师应遵循学生的认知规律，关注学生获取知识的思维过程，引导学生进行动手操作、观察、分析、比较、归纳等环节探寻建构个体知识的“证据”，帮助学生逐步认识二次函数的本质，内涵与特征。在具体教学实践中发现，有的教师对函数内容的教学，虽然知道“数形结合”思想的重要性，但存在教师只注重了“数”而忽略“形”或是只注重了“形”而忽略“数”，未能“数”与“形”有机统一。本文概述人教版《22.3实际问题与二次函数》的教学实例，再谈“数形结合”。

一、探寻从特殊到一般变化，发现规律——寻规

在讲授二次函数时，教师一定要把握一个原则，由特殊到一般的的思想方法。

在掌握y=ax2+k（a≠0）的图像和性质后，再引导学生去探究y=a（x-h）2的图像及性质，类比y=ax2+k（a≠0）的图像及性质，进行观察，比较，归纳，总结出抛物线的开口方向，顶点坐标，对称轴，增减性，极值等。在注意到顶点坐标（0，k）和（h，0）时一定注意两者的區别和联系，这样的探究过程，在很大程度上培养了学生识图能力和画图的能力，并建立起图与式的对应关系，更好的凸显了“数”“形”结合的思想。以此类推，我们系统的学习函数y=a（x-h）2+k的图像与性质时就注意到，实际是将函数y=ax2（a≠0）的图像通过平移得到的，顶点坐标（h，k）和前三个顶点坐标作比较，归纳它们的区别和联系，再一次体会到“数”和“形”的结合。

二、引导建构知识迁移图，识别问题证据——导据

例如在进行《二次函数与实际问题》时就可以这样引入课题，首先板书课题“22.3实际问题与二次函数”先来回顾二次函数有哪几种特殊的结构式及其草图，然后引导学生写出y=ax2+bx+c（a≠0），这里只强调了a≠0条件，对于b，c没有特殊强调，

学生结合解析式去对应的解决二次函数的问题，学生会条理清晰的将问题就会化繁为简。

三、建立函数模型，经历问题解决过程——立本

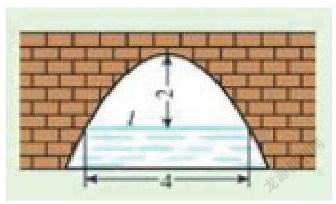
例：如图的抛物线形拱桥，当水面在l时，拱桥顶离水面2 m，水面宽4 m，水面下降1 m，此时水面宽度为多少？水面宽度增加多少？

提出问题：

（1）如何解决这个问题？（小组合作，找出方法）。

（2）如何建立适当的平面直角坐标系（小组合作，并展示成果，学生上黑板建立平面直角坐标系）。

（3）如何结合图像设出适合的解析式（学生思考完成）

（4）如何结合图像确定点的坐标，再确定解析式？（学生小组合作完成，并上黑板展示）

（5）怎样结合解析式解决实际问题？（师生共同完成）

学生通过建立的五种平面直角坐标系再次展开讨论，建立平面直角坐标系的目的，是要确定抛物线的图像，而确定图像一定要有点的坐标，那如何确定点的坐标呢？每个象限内点的坐标都有特点，坐标轴上的点也有特点，这时再让学生进行思考，并且小组交流讨论，然后让学生在黑板上进行标注，让学生感受到建立平面直角坐标系解决问题的强大魅力。紧接着要根据建立的坐标系设出合适的解析式，这就是前面复习二次函数网络图的真正目的，为学生在解决此类问题提供最好的方法。此时教师和学生一起分析图像，图（1）图（4）可设解析式为y=ax2+k，图（2）可设解析式y=ax2，图（3）可设解析式为y=ax2+bx，还可设解析式为y=a（x-h）2+k，还可设解析式为y=a（x-x1）（x-x2），都能轻松的解决抛物线的解析式，图（5）可设解析式y=a（x-h）2+k。结合所设解析式，让学生选择最恰当的图像及确定的解析式解决问题，此时要给学生足够的时间进行思考解题，并讲解。

学生在解决这一问题时，首先建立了如上图中，图2的平面直角坐标系，设出解析式为y=ax2，带入对应的点的坐标确定解析式为y=-1/25x2，求出点的坐标（5，-1）时，学生疑惑了，有的学生回答打1米的柱子。有的学生回答打15的柱子。教师实时引导点拨，结合图像先确定（5，-1）这个点的坐标，结合图像后，学生就不难理解了，要打16-1=15米的柱子。如果选择图（1）则设解析式为y=ax2+k，学生很快确定出函数解析式y=-1/25x2+16，并能确定点的坐标是（5，15），此时，问题能很快得出结论。要打15的柱子。这道练习题再一次体现了“数形结合”的数学思想的重要性。同时也培养了学生一题多解的能力。

通过本节课的学习，学生能深刻感受到二次函数的解析式及其图像的魅力。“数形结合”思想的应用，能让许多复杂的，难以理解的问题简单化，形象化，直观化，让学生的数学思维得到了质的升华。