立德树人视角下平行四边形性质的教学实践研究

齐丹丹 徐琳 李淑华 敖占一

摘要：古人在《左传》中说：“大上有立德，其次有立功”可见，古人很早就意识到做好“立德树人”的重要性。从落实立德树人角度来讲，最为抽象的数学学科承担着培养学生的理性思维、人文品质、应用创新能力、知难而上求真求实等良好人文品质的立德树人方面上发挥着相当重要的作用。平行四边形的性质是几何学习的重点内容，研究如何从立德树人视角下进行平行四边形性质的教学实践研究极有必要。

关键词：立德树人;平行四边形性质;数学学科育人

古人在《左传》中说：“大上有立德，其次有立功”可见，古人很早就意识到做好“立德树人”的重要性。当今信息时代快速发展的背景下，习主席进一步阐明了“立德树人”和人才教育的关系，他提出要在各教育阶段、各教育环节中以立德树人为人才教育目标来促进教学改革与实施。从落实立德树人角度来讲，最为抽象的数学学科承担着培养学生的理性思维、人文品质、应用创新能力、知难而上求真求实等良好人文品质的立德树人方面上发挥着相当重要的作用。《义务教育数学课程标准（2011年版）》中指出数学学科教学中要帮助学生体会学科中所蕴含的文化内涵。

一、学情分析及教学目标分析

平行四边形的性质是人教版义务教育教科书八年级上册第十八章第一小节的新授课。定义本节课的重点是理解并掌握平行四边形对边的性质;定义本节课的难点是经历和理解平行四边形对边性质的探究过程。八年级的学生已经学习了平行四边形的定义、全等三角形证明等相关的几何知识。学生们的逻辑思维能力、抽象思维能力虽然薄弱，但已经具备一定的几何图形性质的探究经验及相关能力，能够进行观察、操作、猜想、验证等数学探究活动。

依据上述分析中八年级学生的知识基础、探究经验、认知思维特点，将平行四边形性质这节课的教学目标设定如下：

知识与技能：理解平行四边形的性质并能应用平行四边形的性质初步解决问题。

过程与方法：在经历观察与分析、猜想及验证、归纳并概括等平行四边形性质的动态软件探究过程中，体验平行四边形性质的生成和发生发展过程;在通过数学演绎证明推理平行四边形性质的猜想过程中，培养逻辑思维能力、几何直观素养和严谨的数学思维品质。

情感态度与价值观：渗透质疑反思求真的科学精神;体会利用信息技术增强解决数学问题的信心，激发探究数学问题地热情。

二、教学过程分析

（一）情境引入

首先，请同学们复习平行四边形的定义。接下来教生共同回顾生活场景中出现的平行四边形，引发学生思考为什么这些生活场景中需要运用平行四边形，具体利用了平行四边形的哪些性质呢？

师：同学们，请问什么是平行四边形？或者说平行四边形的定义是什么呢？

生：两组对边分别平行的四边形是平行四边形。

师：同学们很好的掌握了平行四边形的定义。现在我们一起来欣赏一下生活中的平行四边形，请大家猜猜为什么这些生活场景中要运用平行四边形，或者说利用了平行四边形的哪些个性质呢？

生：好噠，老师。

师：首先，我们一起来欣赏一下生活艺术品中的平行四边形，如图1。接下来，我们一起来欣赏一下封面设计中的平行四边形，如图2。请大家思考一下为啥这两种生活场景要用平行四边形呢？

生：是为了美观。

生：可能是随机选的。

师：哦，那请同学们接下来思考伸缩大门上的平行四边形，如图3。请大家思考为啥伸缩门上的图案要选平行四边形呢？

生：……

师：也仅仅是为了美观，仅仅是随机选取的？那把伸缩门上的图案换成三角形可以不？

生：不可以，门就推不动了，因为三角形具有稳定性。

师：对了，因为三角形的性质不符合推拉门的需求。那既然选择了平行四边形，一定是平行四边形的性质符合推拉门的需求。请同学们思考平行四边形的哪个性质符合推拉门的需求。这就是我们今天就一起来学习一下平行四边形的性质。

设计意图：通过创设生活中平行四边形的场景，引领学生回顾平行四边形的定义这一认知基础，激发学生对平行四边形性质的深入思考，为下一个探究猜想环节进行铺垫。

（二）探究猜想

平行四边形对边关系

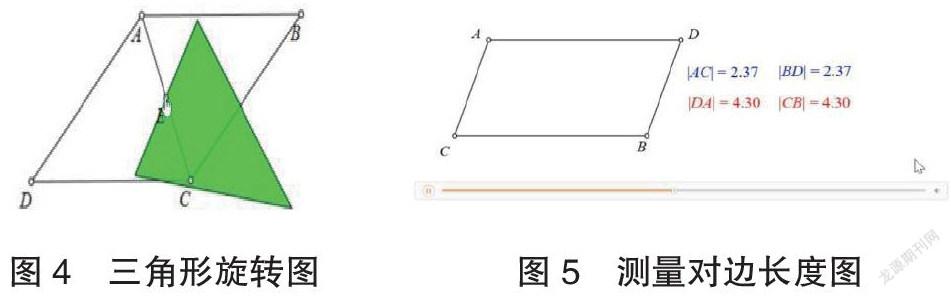
1.让学生观察皓骏动画，以三角形ABC边AC中点E为旋转中心，旋转三角形ABC，我们观察发现当三角形ABC旋转180度后完全与三角形ADC重合。

2.数学活动，测量平行四边形的四条边的长度，并且记录下数据，观察发现AB与DC，AD与BC间的长度关系。

经过测量一组对边AC和BD的长度我们得到AC=BD=2.37，测量另一组对边我们又得到DA=CB=4.30，拖动点C，平行四边形四条边的长度发生变化，观察发现无论平行四边形怎样变化，对边长度都相等。

3.猜想：平行四边形两组对边相等

有上述探究过程可以猜想出：平行四边形的对边相等。但数学除了显而易见的猜想，我们更需严谨的数学证明。

设计意图：首先，从三角形旋转的皓骏动画模型中，可发展同学们的几何直观素养。其次，测量平行四边形对边长度的数学活动中，培养学生质疑探究、手动验证的数学证明思路。养成其解决几何类问题的信心，获得探究平行四边形对边性质的成功经验。最后，通过皓骏数学软件的动态直观演示突破平行四边形性质一节课的重点、难点。

（三）新知证明

已知四边形ABCD是平行四边形，求证其对边相等。即证明AB=CD，AD=BC.

证明：如图，连接线段AC，∵四边形ABCD是平行四边形，∴AD||BCAB||CD，∴∠DAC=∠ACB，∠DCA=∠CAB.又∵AC是△ABC、△CDA的公共边，∴∠△ABC≌△CDA（ASA）.

教师启发学生通过复习三角形全等进而证明平行四边形对边相等的性质

设计意图：教师提出问题，根据上述皓骏动画启发，适当引导，利用已有全等三角形的识，添加辅助线，构造全等三角形，从特殊到一般使得平行四边形性质的难点得以突破。

（四）新知应用

如图，四边形ABCD是平行四边形，且AB=10，AD=8，AC⊥BC。求BC，CD，AC，OA的长？

根据咱们刚刚学习过平行四边形的对边性质，求解上述问题。

设计意图：培养学生概括总结能力以及综合运用平行四边形性质解决问题的能力及学生逻辑思维的严谨性，激发学生学习的应用兴趣。

（五）归纳小結

1.同学们，咱们学习了平行四边形对边的性质后，你在知识方面、数学思想方面有哪些收获？

请学生谈对平行四边形对边性质一节课的学习感受，帮助其梳理、概括本节课的性质探究过程和结果，进一步回顾其所蕴涵的数学思想方法.

2.启发留疑平行四边形对角的关系，激发学生的求知欲，充分利用学生好奇心与探究欲。拓宽学生思维与视野，培养其直观想象、数学抽象的学科核心素养。

设计意图：帮助学生对平行四边形对边性质及其思维、情感态度等进行梳理。

三、课后反思

（一）课堂教学反思

《义务教育数学课程标准（2011年版）》指出要注重数学学科中育人的功能”。本节课注重学生对平行四边形性质的猜想和证明过程。尝试基于布鲁纳的学习理论及认知发现过程等相关的教育教学理论，借助Hawgent皓骏动态数学软件和PPT等现代教学软件，完善动态平面几何教学的教学基本模式，即通过拖动改变平行四边形的位置，猜想并且验证平行四边形的性质，激发学生空间想象与创造力。

本节平行四边形对边性质的探究课注重数学学科德育的培养，如本节课中所运用的Hawgent皓骏动态软件将几何学中的平行四边形对边性质的探究过程动态直观化，培养学生进加理解数学、热爱数学，进而培养其数学质疑反思精神、探究求证品质、求真精神等学科德育，落实数学学科立德树人的育人效果。

（二）学生课后反馈

学生对平行四边形对边性质探究过程及探究结果的反映良好。所实验班级共有39名同学，其中喜欢这种学科育人方式的学生达到92.3%;在对学生进行课后访谈的过程中，学生也对数学学科育人融入数学课堂教学表现出了很明显的支持态度。

T：同学，请问你对课堂哪个环节的印象比较深刻，或者喜欢课堂的哪一点都可以说一说。

S1：老师启发我们平行四边形的性质为什么要在生活中存在时，我对那个环节的印象还深刻。

T：为什么呢？

S1：因为这次我们有时间慢慢想、老师也允许我们慢慢想，老师也没有否认我们的想法。我感觉数学很好，生活中的数学很有道理，嗯，就是很有用吧。

T：同学，请问你对课堂哪个环节的印象比较深刻，或者喜欢课堂的哪一点都可以说一说。

S2：我对这几课的动画展示比较印象深刻。

T：为什么呢？

S2：因为这个环节给了我们机会让我们直接看到数学结果，思考起来我感觉就比较容易了。而且要是数学都这样讲的话，我感觉我的数学成绩肯定更好。

T：要是以后我没有创设这个动态演示的动画，你还认为数学容易吗？

S2：要是以后没有的话，我要是自己能做动画，我就自己用动画学数学了。嘿嘿。

从上述两位同学的访谈，我们可以得知，数学学科中需要创造教育等待的时间和机会，这样才能引发学生数学思考，继而激发他们对数学学科的热爱和追求。给予他们克服数学困难的信心和勇气。所以数学课堂中需要育人，也大有数学学科育人的土壤等待我们课程设计者的开发。

本文是河北民族师范学院校级一般项目科研课题：立德树人融入数学学科教学实践研究，课题编号：PT2018014的研究成果。

参考文献：

[1]左丘明.春秋左传[M].哈尔滨：哈尔滨出版社，2016.

[2]中国人民共和国教育部制定.义务教育课程全标准[M].北京：北京师范大学出版社，2012.