基于问题串 从浅层走向深度

黄世贵 刘贤虎

摘 要 “分段计费”一课教学设计通过问题串引导学生自主探究、协同学习，以知识结构和数学思想方法为主线，教学结构变“教师讲授为主”为“教、学、做”合一与多元交互。学生在结构化的探究中形成结构化思维，从浅层学习走向深度学习，在学习中学会学习。

关键词 分段计费 问题串 结构化 浅层深度

《义务教育数学课程标准（2011年版）》（以下简称《数学课程标准》）中指出：“教师要引导学生独立思考、主动探索、全体交流，使学生理解和掌握基本的数学知识与技能，体会和运用数学思想方法，获得基本的数学活动经验。”[1]如何培养学生的学习能力，可以先将每节课的核心问题与学习任务整合，分解成逻辑关联、层层深入的问题串，一次性呈现，让学生独立思考，主动探究，相互协同，交流反馈，进而得出结论，形成较为深刻的认识，实现深度学习。下面以人教版小学数学五年级上册“分段计费”为例，谈谈具体做法。

一、基于深度学习的教学目标设计

1.让学生经历观察、分析等数学活动，自主探究分段计费问题的数量关系，能运用分段计算的方法正确解答这类实际问题，进一步提升解决问题的能力。

2.在分段计费问题的解决过程中，培养学生独立思考的意识，能从不同的角度分析和解决问题。

3.学生体会解决问题的一般方法，积累解决问题的活动经验，初步感悟函数的思想。

教学重点：运用分段计算的方法正确解决分段计费的实际问题。

教学难点：探究分段计费问题的数量关系，积累解决这类问题的活动经验。

二、教学过程

（一）问题引发，感知计费规则

问题1：同学们，你们跟爸爸妈妈坐过出租车吗？知道打车的费用是如何计算的吗？

预设：①根据打车的里程和乘车时长综合计算出来的，路程越长，时间越久，所需要的费用就越多。

②我还知道打出租车有起步价，比如3公里以内11元;超过的部分再另外计费。

问题2：我国某个城市的出租车计费标准：3千米以内7元;超过3千米的部分，每千米加收1.5元（不足1千米，按1千米计算）。李叔叔有一次打出租车，下车时付了7元，那出租车的里程表显示的千米数可能是多少呢？

问题3：如果里程表显示行驶了4千米，李叔叔还是付7元吗？

预设：不是7元，而是付8.5元，因为根据计费标准，前面的3千米收费7元，后面的1千米属于超过3千米的部分，要另外加收1.5元，所以是7加1.5等于8.5元。

问题4：原来要将4千米分成了3千米和1千米两个部分，根据收费标准分段计费再相加算出车费。可见打车时计费不是完全按千米数×单价来计算的，需要分段。那出租车到底是怎样计费的呢？这节课我们就一起来研究生活中的分段计费问题。

设计意图：教师从打车的生活情境入手，结合学生的生活经验，初步感知分段收费。接着以李叔叔付7元里程表可能显示的千米数设疑，引发学生进行猜测、分析。在整理信息、理解信息中，学生逐步明确打车计费不是按照千米数×单价来计算，需要分段，而且每一段的收费标准不一样，这为后面的深入研究打下基础。

（二）问题探究，尝试计费方法

师：你们是想老师带着大家一步一步的去研究这个问题，还是自己和同伴一起研究？我们该如何研究这个问题呢？

预设：①和同伴一起研究。我可以举例子，比方说甲乘客坐了多少千米，要求需要付多少钱;乙乘客坐了多少千米，要求需要付多少钱等等。

②我们在解决了这一类问题之后再总结规律，看看这一类问题该怎么解决。

师：数学的许多规律、法则、方法等，都是通过例子来说明的。这里就有一个例子，请看学习单：

问题1.杨叔叔坐了6.3千米，他应付多少钱？（想一想，算一算）

问题2.请你尝试完成出租车价格表，除了用表格的形式表示收费情况，你能用其它的方式表示出分段收费吗？ （填一填，画一画，说一说）

问题3.怎样解决分段计费的实际问题？（想一想，写一写，说一说）

师：下面请同学们先独立思考，我们先解决第一个问题。如果遇到困难，可以向周围的同学小声请教;完成得比较快的同学，也可以主动地帮助有困难的同学。

设计意图：这一环节一次性呈现本节课主要研究的3个问题，从具体的数据计算，到制作价格表、画线段图等，再到分段计费方法的总结概括，逐层深入，整体呈现。学生前面对分段有了一定的认识，为完成这3个问题的探究打下良好的基础。部分学生虽然对解决第3个问题有困难，但是积累了一定的思考，在启发下，思维就会生长发芽。

（三）互动建模，理解分段计费

师：谁来说一说自己对第一个问题的想法？

预设：①前面的3千米是按7元来计费的，所以我是这样计算的，6.3减去3等于3.3千米，3.3千米要按4千米计费，应该是1.5乘4再加7等于13元。

②先把6.3千米看作7千米，将每千米按1.5元来计费。那就是1.5乘7等于10.5元，前面的3千米只用了4.5元，根据计费规则，前面的3千米是按7元来计费的，这样就少付了2.5元，所以最后的收费应该是10.5元加上少收的2.5元等于13元。

师：如果行驶里程是8.7千米，应该怎样进行计算？为什么6.3千米、8.7千米都是用7元加上后面里程的费用？

预设：因为按照收费标准，前面3千米一定是7元，这个收费标准是固定的。只是后面里程不同，費用也不相同。都是要把这两部分相加。

学生接下来完成第二、三个问题。

师：下面一起来分享一下对第二个问题的想法。

预设：出示表格（表1）。前面的3千米都是计费7元，到4千米时是8.5元，5千米时是10元，6千米时是11.5元，以此类推。

师：大家都非常善于发现规律，我们除了可以用列表法来表示出租车的计费情况，还有别的方式吗？

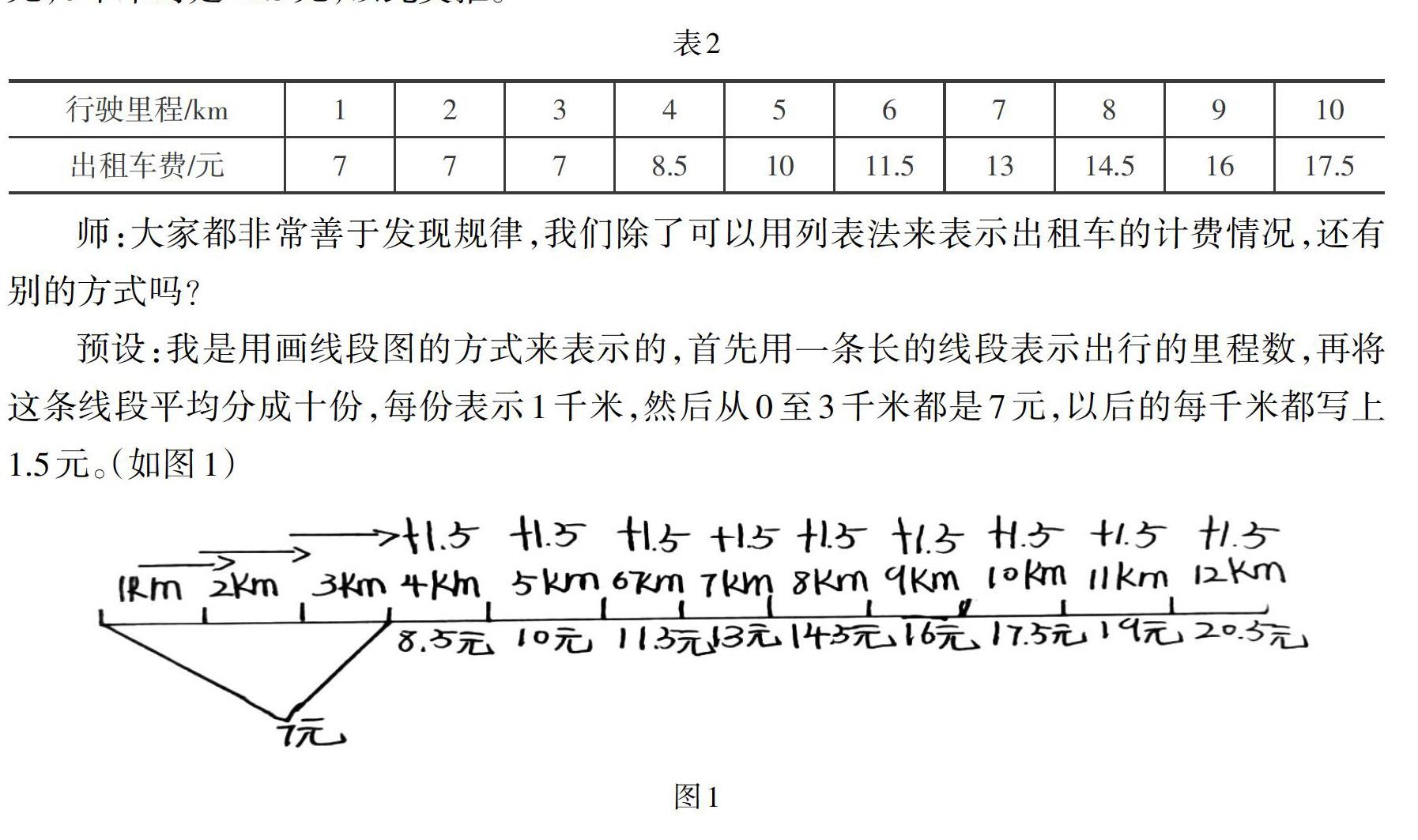
预设：我是用画线段图的方式来表示的，首先用一条长的线段表示出行的里程数，再将这条线段平均分成十份，每份表示1千米，然后从0至3千米都是7元，以后的每千米都写上1.5元。（如图1）

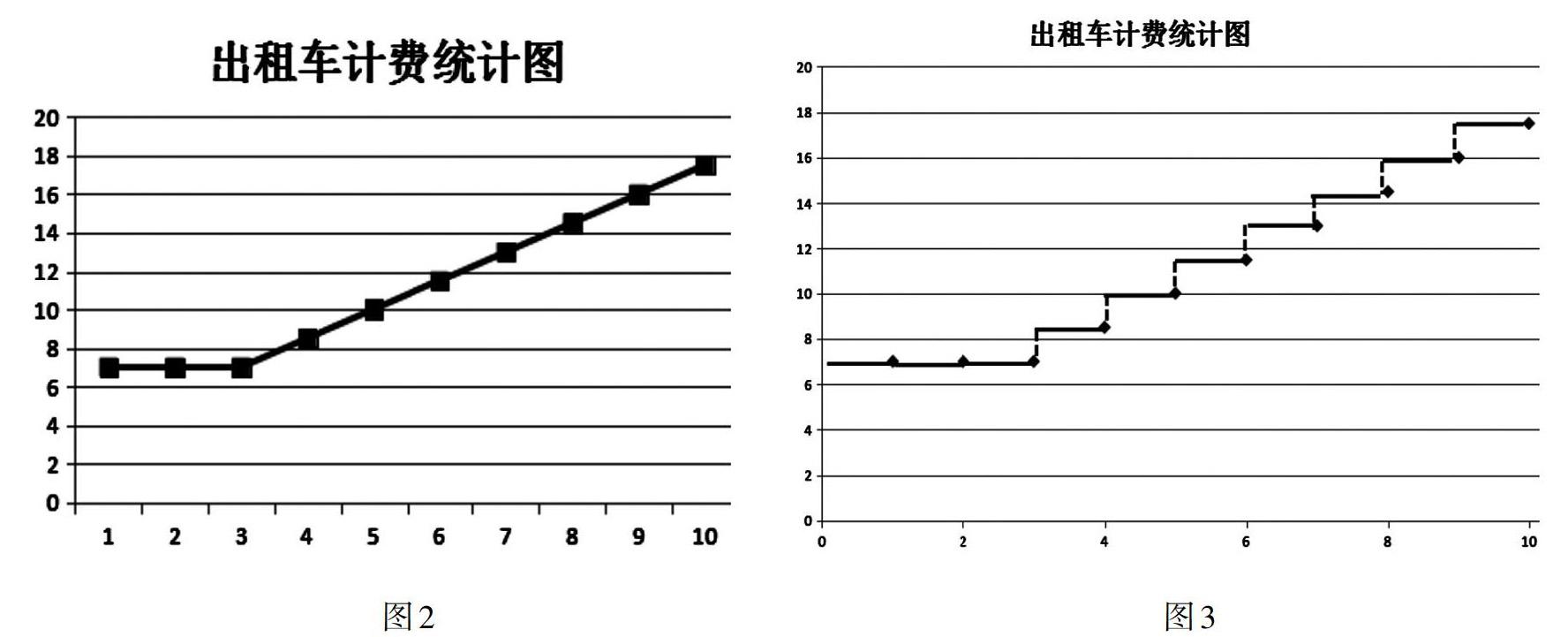
师：谁看懂了他的想法？下面的图2和图3哪一种统计图表示更准确？

预设：图3表示更准确，因为每一段的费用是一样，不是一种直线上升的过程，应该是一种阶梯状。

师：对于第三个问题，谁又有什么想法呢？

预设：①我觉得解决分段计费这样的实际问题，首先要理解它的计费规则，然后要明确每一段是怎样计费的，最后再把两段的费用相加。

②我觉得最重要的是如何分段，要根据计费规则来分段，比如问题1中的6.3千米看作7千米以后，要把7千米分成3千米和4千米的两段，而不能分成2千米和5千米。

小结：在理解计费规则的基础上正确分段，后面一段要用“进一法”保留整数来计算，这些是解决分段计费问题的关键。

师：出租车为什么要分段计费呢？

微课介绍：出租车收费既有固定部分又含可变部分的方法，起步价是为了保证出租车司机的收益，接近大部分出租车的实际成本。按路程计算收费，太短的路程对几乎所有运输业来说成本都比较高。这种收费结构降低了出租车的里程费，乘客无需为较长的行程支付高于实际成本的价格，对于较短行程，也能保证出租车运行成本。

设计意图：学生在汇报交流中思维不断碰撞，逐步提升自己的理解和认识。互动建模分为三个层次，第一层次理解分段的含义，知道如何分段以及后面一段要先用进一法取近似值，再乘单价。第二层次学会用表格来表示分段计费的规律。第三层次尝试用线段图来表示、理解和解释分段收费。在多元表征的同时，学生找到不同表征之间的联系，感受行驶里程与车费的变化规律，初步体会函数思想，进而概括出分段计费的计算方法，促进学生的理解和内化。

（四）解决问题，应用分段策略

问题1.编一编：某市自来水公司为鼓励节约用水，采取按月分段计费的方法收取水费。12吨以内的每吨2.5元;超过12吨的部分，每吨3.8元。

请你根据以上信息，补充一个条件后，提出一个数学问题并解答。

问题2.选一选：五（1）班35名师生照相合影。每人一张照片，一共需付（   ）钱？ （一共需要35张照片。需要加印30张。）

（1）27.5+2.5 × 35

（2）30 × 2.5+27.5

（3）27.5+（35+5） × 2.5

问题3.比一比：王阿姨要把2.5千克的物品从东莞市寄往广州市（同属广东省），她选择哪家快递费用比较便宜？

①号快递：省内1千克以内10元，每超过1千克加收2元;省外1千克以内15元，每超出1千克加5元。（不足1千克按1千克计算）。

②号快递：省内1千克以内9元，每超过1千克加收3元;省外1千克以内12元，每超出1千克加8元。（不足1千克按1千克计算）。

师：在生活中，除了水费、电费、冲洗照片和快递采用分段计费以外，还有邮局寄信函，打固定电话、停车场收费等等，很多时候也是采用分段计费的，那它们又是如何计费的呢？这个问题就留给同学们课后去调查解决，希望大家都有一双敏锐的眼睛，用数学的眼光去观察，用数学的思维去分析生活中的数学现象，做一个热爱生活、善于运用数学知识解决问题的好孩子！

设计意图：解决问题环节安排了三道题，第一题学生编题有两种可能，一是直接用单价×数量计算，二是需要分段计算，让学生在对比中感受一般计费和分段计费的不同和联系。第二题是不同情境下的分段计费，对“含5张照片”学生容易理解错误。第三题是综合运用分段收费解决问题。这些问题都需要学生运用数学模型，学以致用。教师不是停留在评判对错上，而是充分让学生去分析、思辨、创造，进一步深化对分段收费的理解和运用，发展学生的思维。

三、总结反思

本节课较好地体现了数学“问题教学”的教学理念，它从教的设计转向学的设计，以知识结构和数学思想方法为主线，教学结构变“教師讲授为主”为“教、学、做”合一与多元交互。课堂文化则主张“支持和激励的学习氛围、独立和协同的学习机制、结构化和板块化的教学”[2]。其教学核心指向以下两点：

（一）由浅层转向深度

对知识的理解是深度学习的开始，在此基础上，学生才会整合相关知识去运用、评价。本节课通过问题引领，促进学生由浅层感知转向深度学习。首先，创设问题情境“付7元猜测可能坐的里程数”，从而引发本节课的本原性问题“出租车的计费为什么不是千米数×单价”，在唤起学生认知基础的同时，激发学生探究的欲望。当学习内容和儿童的经验建立联系时，便于促进儿童的理解，尝试复杂问题解决。其次，由本原性问题分解成三个问题并以问题串呈现，这些学习任务具有挑战性，不能依靠记忆和模仿简单问答，学生必须要选择深度学习的方式来分析、解决。同时三个问题后面都有提示要点，指引学生如何走向问题解决。

问题串的整体呈现和解决让学生对整节课的学习有了整体的认识，并且在研究的过程中，学生逐步总结出分段计费问题的解决思路与策略，形成结构化思维，提升深度学习能力。

（二）从学会走向会学

让学生学会学习，就要把学习的主动权交给学生，意味着教师要从课堂的中心往后退。好的课堂应该是讲着讲着教师不见了，学生成为了学习的主人[3]。教师只是在适当的时候进行点拨、指引，一是将模糊不清的认识进行辨析，变为清晰;二是将对话的话题指向知识的本质，走向深刻。让学生学会学习，就是教师不能只关注怎么教，而是要围绕学生的学进行教学设计，关注学生有没有学会、学会了什么、怎么学会[4]。同时，课堂的对话也应摒弃一问一答的局面，而应让“生生对话”成为主旋律，让语流在课堂流淌起来，这样学生才能在自主、探究、思辨、协作中学习如何学习。

让学生学会学习，就要让学生去发现问题、提出问题、分析问题、解决问题。本节课研究的主要三个问题呈现进阶的关系，学生在这种板块化的探究中逐步形成结构化的思维。从具体到理性认识，从个例到普遍规律，整个探究的过程就是人类认识世界的历程和学习发现的一般方法，学生经常经历这样的学习过程，在问题解决的同时，掌握有效的学习策略。

授人以鱼不如授人以渔，借助复杂问题解决，学会深度学习，才是立足于未来社会的关键能力。

[参 考 文 献]

[1]教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012：3.

[2]梁淑颖.寻问题根源，觅解题佳径：“分段计费”错因分析与再思考[J].教师，2019（24）：69-70.

[3]刘贤虎.基于深度学习的问题教学略论：以小学数学教学为例[J].中国教师，2019（11）：77-79.

[4]杨惠娟.渗透数学思想方法 发展学生数学素养：以“小数的含义和读写”教学为例[J].小学数学教育，2017（6）：36-37.

[5]崔允漷.指向学科核心素养的教学即让学科教育“回家”[J].基础教育课程，2019（Z1）：5-9.

（责任编辑：杨红波）