侵彻效应混凝土靶HJC本构模型研究

米振国， 石云波， 张 婕， 滑志成， 都捷豪

(中北大学 电子测试技术重点实验室，山西 太原 030051)

0 引 言

由Holmquist，Johnson和Cook提出的混凝土材料（HJC模型）得到了广泛的认可，此种模型是一种简单有效的混凝土模型[1]。压缩是指在承受正静液压的压力状态，拉伸指在承受负静液压的压力状态[2]。Tu等[3]对RHT模型动态拉伸时的模型进行修正，假设断裂能是恒定的，则断裂应变随着张力应变率的增大而减小。但是，最近相关的抗拉强度和断裂试验表明，断裂能随着应变率的增加而增加。HJC模型以材料压缩损伤演化为主，较好地考虑了压缩强度的压力相关性、应变率效应和损伤软化效应，适用于大应变、高应变率和高压作用下的混凝土的损伤破坏情况[4]。所以，采用HJC本构模型进行数值模拟对穿甲弹侵彻厚混凝土靶有重要意义。

混凝土HJC本构模型包括基本的力学参数、强度参数、压力常数、损伤参数共19个和2个软件常数。陈星明等[5]采用数值模拟方法进行HJC 本构模型抗侵彻性能的参数敏感性研究，通过多次修改数值模拟得出 HJC 模型的抗侵彻敏感参数，并对其不合理进行调整。汪衡等[6]为了获得该模型参数对侵彻毁伤效应影响的灵敏度，分类给定参数的调试范围得到对侵彻效应的余速影响较大的参数，确定一组较为合理的基准参数。任根茂等[7]基于普通混凝土的准静态单轴压缩实验、三轴围压实验、一维 SHPB 实验和一维平面应变Hugoniot冲击压缩实验数据，确定了一组适用于不同强度普通混凝土材料 HJC 本构模型的强度参数、率效应参数和状态方程参数取值。由于他们研究的弹体和靶体都较小，速度比较局限，将其运用到穿甲弹侵彻厚混凝土靶时，侵彻经历的时间和加速度峰值都偏差明显。

针对上述问题，通过数值模拟获取一组适合130 mm穿甲弹侵彻的模型参数，分析影响加速度大小的主要参数。通过加速度可以分析出穿甲弹的运动状态和混凝土的受力情况，所以对于测量加速度是必要的。由于试验环境恶劣，采取弹载测试采集存储系统进行测试，通过加速度传感器获取电压信号，通过电路放大并进行存储。试验结束，对取回来的系统进行读数，利用Matlab分析处理获得加速度信号，并对数值模拟结果进行验证。

1 有限元建模

1.1 模型的基本尺寸和形状

采用直径为130 mm的穿甲弹穿过混凝土靶，如图 1所示，混凝土靶的尺寸为 2000 mm×2000 mm×3000 mm。

图1 穿甲弹和靶体几何尺寸

1.2 有限元模型及材料参数

1.2.1 建模

将穿甲弹和混凝土两部分建模，如图2所示。

图2 1/4有限元模型

对于混凝土的贯穿和侵彻，计算结果与混凝土的建模方法、网格尺寸等相关[8-9]，单位采用cm-g-µs。由于网格划分对试验影响较大，仿真表明，侵彻穿甲弹半径与靶板网格边长比值在6.0左右，计算结果比较准确。本试验采用的130 mm穿甲弹侵彻混凝土，所以将网格设置为1 cm，穿甲弹不计算损伤，不考虑侵蚀及失效。混凝土靶计算损伤，考虑侵蚀及失效。利用弹结构和载荷的对称性可节省计算时间，取弹和靶实体模型的1/4进行建模和求解，采用拉格朗日计算，弹和靶体均采用八节点六面体三维实体单元进行网格划分，弹经过混凝土区域进行网格加密处理，其他区域的网格由内向外稀疏。

1.2.2 模型分析

弹丸材料使用35CrMnSi低合金超高强度钢，在侵彻过程中几乎没有质量的侵蚀和变形。所以在侵彻过程中可以把穿甲弹看作刚体。混凝土选用HJC模型，该模型适用于大应变、高应变率和高压作用下的混凝土损伤破坏。HJC本构模型主要包括强度模型、状态模型和损伤模型3部分。

其屈服面方程表示为

如图3所示，其中D是损伤参数, P1=P/fC′（P为实际压力）是归一化压力,（为真实应变率，为参考应变率）是无量纲应变率。归一化等效应力（σ 为实际等效应力，为材料准静态单轴抗压强度）。（T单轴抗拉强度）为材料的最大特征化等效应力。A为归一化内聚强度，B为归一化压力硬化系数，N为压力硬化指数，C为应变系数。

图3 屈服面方程

状态方程主要考虑混凝土压缩阶段采用三段式的方式来描述混凝土的静水压力P和体积应变µ之间的关系，其中µ=ρ0/ρ–1。混凝土拉伸阶段只有一小段是正比关系接着就是稳定值。所以拉伸时，当拉力增大到一定值，体积不再随其增大而增大，混凝土裂缝贯通断裂增大，本文主要研究侵彻过程的加速度和速度，不考虑混凝土的碎裂情况，所以模型适用。

1.2.3 模型参数

现在所采用的仿真模型主要参数的确定方法主要有：采用大数据认可的数据，在套用数据仿真模型的基础上进行修改[10]；通过实验的方法获得关键参数[11]；通过经验公式获得部分参数[12]。

由于缺少实验条件和数据，且损伤参数D1和D2对数值模拟结果影响较小，一般取0.04和1。B和N可由σ*和p*的曲线拟合得到，取1.58和0.84。参考应变率EPSO和失效参数FS为软件参数，均取默认值1。混凝土的密度ρ为2.43 g/cm3，剪切模量G为13 GPa，根据熊益波的塑性理论推导得出A为0.28[13]。抗压强度实测41.3 MPa，根据公式单轴抗拉强度得4 MPa, 根据公式压碎压力，取13.4 MPa，压碎体积应变，取0.001。最小断裂应变 EFmin取0.01、压实压力µl取0.14，应变率最大系数C取0.06，压实压力Pl取1.11 GPa，归一化最大强度SFmax取11.0，压实后PV 曲线 K1、K2、K3取 0.85 GPa、1.71 GPa、2.08 GPa。

考虑试验的误差，分析参数的相关性和取值范围，分别对剩余的19个参数取±10%的调试范围，共计38次。

2 数值模拟

建立有限元计算模型时，因为实验过程中瞄准靶中心发射，所以为了减少计算时间，节约成本，利用穿甲弹和靶体的对称性，取1/4结构实体建立模型。模型中设置的接触类型为面面接触，并在接触算法中添加基于拉伸损伤失效准则，由用户定义的失效主应变和失效剪切应变，当单元的有效应变达到失效主应变和失效剪切应变时，单元失效；当表面单元失效后继续在结构内部重新定义新的接触面。混凝土模型的上下面为自由面，对靶体四周进行了约束，混凝土靶相对不动。穿甲弹初速度为760 m/s，混凝土靶为 200 cm×200 cm×300 cm 的长方体，穿甲弹垂直于靶体中心侵彻。

2.1 加速度曲线和速度曲线分析

选取穿甲弹整体为A，分别得到其加速度以及速度曲线如图4和图5所示。

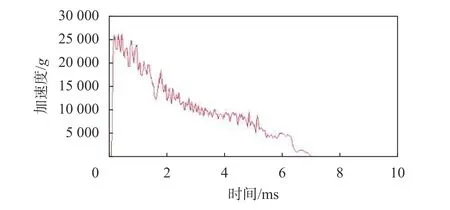
图4 加速度曲线

图5 速度曲线

由数值模拟过程可以看出在侵彻中，穿甲弹从侵彻开始加速度迅速增大，这是弹头侵入过程，随后由于弹体的摩擦等阻力，加速度略微增加，直到弹体完全侵入，加速度达到最大值，随后开始缓慢减小。本次侵彻过程中加速度为26000g，侵彻脉宽为 6.6 ms，速度为 312 m/s。

2.2 影响加速度峰值的参数分析

通过数值模拟分析可知，对加速度峰值大小影响程度依次为Pc、EFmin、B、N、T、、A、、C、G、、K1、D1、Pl、D2、ρ、SFmin、K2、K3。其中Pc影响最大达到了 16.5%，EFmin、B、N、T、、A影响分别为7.3%，6.6%，6.4%，6.1%，5.5%，5.2%。

130 mm 穿甲弹在以 760 m/s速度侵彻 3 m 混凝土靶时，对加速度峰值影响最大的是压碎体积Pc，在加速度峰值差距较大时，可重点调试。

3 靶场试验数据分析与处理

改造过的130 mm穿甲弹，弹体内部搭载数据记录仪以及待测系统，弹体质量为25.6 kg，弹头采用锥形弹头，质量为10.4 kg，穿甲弹整体质量为36 kg。本次试验侵彻靶体类型为C40混凝土靶，规格为 2000 mm×2000 mm×3000 mm。混凝土靶及穿甲弹回收如图6和图7所示。

图6 C40混凝土靶

图7 穿甲弹回收

试验弹尾部装配有弹载测试存储单元，采样恒定采样，延时时间满足之后，储存模块记录高g值加速度传感器的数据经量化编码后存入Flash芯片中。实际侵彻速度约为760 m/s，靶体前方相距2 m有标志物，通过观察高速摄影可以获得弹丸的侵彻历程，侵彻如图8所示。

图8 高速摄影

由高速摄影结果可得，穿甲弹侵彻入靶到出靶时间约为5.875 ms。利用上位机读取存储器采集到的电压信号，将其转换为加速度信号，然后进行1000 Hz低通滤波，穿甲弹侵彻原始数据以及侵彻滤波曲线如图9和图10所示。

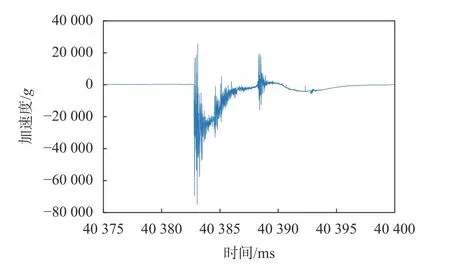
图9 弹丸侵彻原始数据图

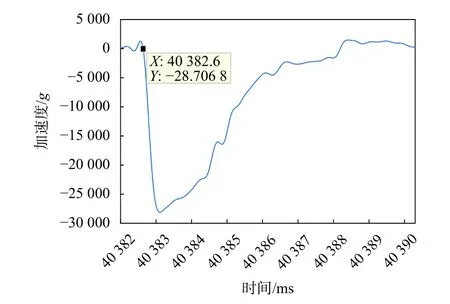
图10 弹丸侵彻滤波数据图

由图可知，穿甲弹在 40382.6 ms时入靶，最大过载值为27756g。针对这加速度区间以初始条件760 m/s进行一次积分获得弹丸的侵彻速度曲线，二次积分获得穿甲弹的侵彻位移曲线，见图11和12。

图11 弹丸侵彻速度曲线

在穿甲弹侵彻位移曲线上取3 m可以获得弹丸侵彻穿出靶体的时间，为 40388.4 ms，侵彻脉宽为 5.8 ms，穿甲弹以 760 m/s速度侵彻 C40混凝土靶的穿出靶体之后速度为268.7 m/s。试验结果与仿真结果基本一致，模型具有可参考性。

图12 弹丸侵彻位移曲线

4 结束语

基于数值模拟、靶场试验、数据分析方法，得到了一组适合130 mm口径弹侵彻混凝土的HJC模型。通过对模型中关键参数取10%的进行数值模拟，得到各个参数对加速度峰值影响程度。将弹载采集存储系统装配到改装的弹体中进行火炮试验，将得到的电压信号转化为加速度信号，对其进行两次积分依次获得其速度和位移。通过实验结果与数值模拟对比，验证了模型的准确性。