基于改进粒子滤波的锂离子电池剩余寿命预测
2021-09-10蔡艳平苏延召
陈 万, 蔡艳平, 苏延召, 姜 柯, 黄 华
(火箭军工程大学,陕西 西安 710025)
0 引 言
锂离子电池在实际应用中的安全问题一直是人们关注的焦点[1-3],而预测与健康管理(prognostics and health management,PHM)技术能够有效监控锂离子电池的健康状态,提高电池工作时的安全性。其中准确的剩余寿命(remaining useful life,RUL)预测是实现PHM的基础,因此成为当前研究的热点。
基于上述问题,本文提出了一种随机扰动无迹粒 子 滤 波 ( randomly perturbed unscented particle filter, RP-UPF)算法,首先采用UKF算法获得的建议分布来产生PF算法的粒子集,然后采用随机扰动重采样算法优化PF的重采样过程。改进算法相对于基本PF的优势在于:一定程度上克服了PF粒子退化和粒子多样性不足的问题;在进行重采样时,只对保留下来的有效粒子进行处理,一定程度上减小了算法的计算量。在此基础上构建了基于RPUPF的锂离子电池RUL预测方法,实现了锂离子电池RUL预测。
1 标准PF原理及其改进
1.1 标准PF及其不足
PF算法是一种基于蒙特卡洛仿真的近似贝叶斯滤波算法,核心思想是用一些离散的采样点近似随机系统的概率密度函数,以样本均值代替积分运算,从而获得状态的最小方差估计[12]。其实现过程有为:初始化、重要性采样、权重更新及归一化、重采样、状态估计,其中重要性采用和重采样对PF算法的性能影响最大。重要性采样是将粒子集带入重要性函数来更新粒子集,而对于标准PF来说,重要性函数一般选择先验密度。重采样是通过对样本进行采样,大量复制权重较高的粒子,淘汰权重较低的粒子,常用的重采样方法有随机重采样、多项式重采样、系统重采样和残差重采样。
然而基本PF算法存在粒子退化和粒子多样性不足的问题,这是由于先验分布产生的粒子不一定能反映真实分布以及重采样中大量复制粒子导致粒子多样性下降。因此可以从重采样算法和重要性函数的选择两方面对PF算法进行改进。
1.2 算法改进
在重要性函数的选择方面,采用UKF算法获得的分布作为重要性函数。UKF算法的核心思想是利用无迹变换在估计点附近确定采样点,用这些样本点表示的高斯分布来近似状态的概率密度函数。通过UKF获得的分布能够更加接近真实分布,因此PF通过该分布获得的粒子集能够更加接近真实分布,可以减缓PF的粒子退化问题。
在重采样算法的优化方面,提出了随机扰动重采样算法。其实现过程如下:


1.3 随机扰动无迹粒子滤波算法
RP-UPF算法使用UKF产生的建议分布作为算法的重要性函数,使用随机扰动重采样算法实现粒子集的重采样,从而克服粒子退化、增加粒子多样性,并在一定程度上减小计算量。其实现步骤如下:

当循环次数k小于设定的循环周期数T,令k=k+1,返回步骤2)进行循环,否则终止循环,算法结束。
2 RUL预测框架
2.1 实验数据
实验数据采用的美国国家航空航天局(National Aeronautics and Space Administration, NASA)公开的数据集。NASA使用Li-ion 18650型号电池进行了容量衰退实验并获得了不同实验条件下电池容量衰退的数据集,其中包括4块电池:B0005、B0006、B0007、B0018,电池的额定容量为2 Ah。实验在室温(24 ℃)下进行,其实验过程如下:
打扑克,我不含糊。不过,这次可得小心,这猴子没安好心。在大姑娘面前戴套包,那可丢透人了,我孟浪地抓牌,恨不得把好牌都抓到手,大家也很紧张,想必心情是一样的。
1)充电:首先进行恒流(1.5 A)充电,当电池电压达到4.2 V后,改为恒压充电,当充电电流下降到0.02 A时充电完成。
2)放电:恒流(2 A)放电直到 B0005、B0006、B0007和 B0018的电压分别下降到 2.7 V,2.5 V,2.2 V和2.5 V时放电完成。不同电池单次放电的截止电压是随机设置的,目的是模拟电池的真实使用情况。
2.2 经验模型
研究表明[8,10],经验模型中的双指数模型能够较好地拟合锂离子电池的退化数据,其表达式如下:

利用双指数模型拟合4块电池的退化数据,拟合结果如图1所示,拟合方法采用的Matlab的曲线拟合工具箱。从图可以看出双指数模型可以较好的拟合数据,因此可以作为电池的退化模型。同时可以获得拟合曲线的4个参数a、b、c、d的值,结果如表1所示。本文将B0005的退化数据作为历史退化数据用于求解模型参数的初始值,因此模型参数的初始值为双指数模型拟合B0005退化数据的结果,其余3块电池的退化数据用于预测。
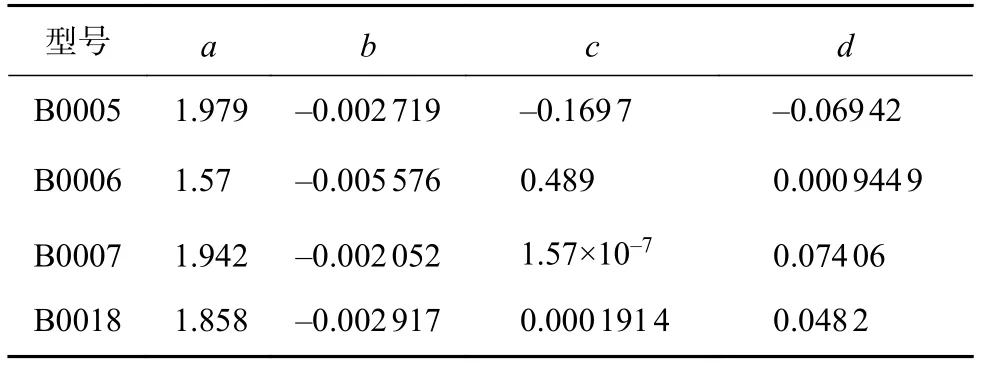
表1 模型参数及均值
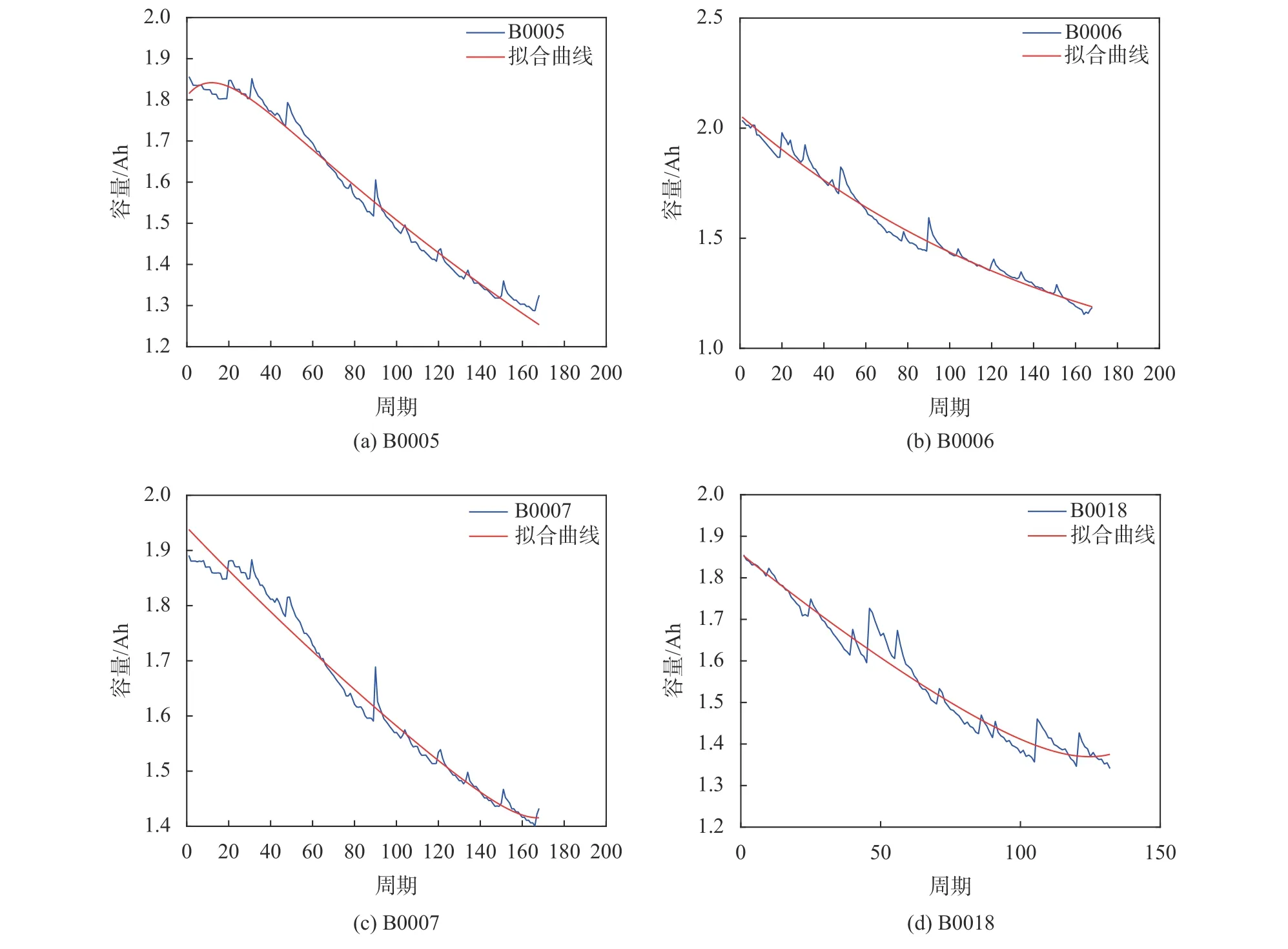
图1 4块电池的退化数据和拟合曲线
2.3 基于RP-UPF的锂离子电池RUL预测方法
1)读取用于预测的锂离子电池退化数据。本文中读取的数据为B0006、B0007和B0018。
2)初始化。设置粒子数、过程噪声方差、测量噪声方差、失效阈值、预测起点以及模型参数的初始值。本文中粒子数设置为1000,失效阈值设置为额定容量的70%,即1.4 Ah,但由于B0007的退化数据未达到1.4 Ah,因此B0007的失效阈值设置为额定容量的 75%,即1.5Ah。模型参数的初始值设置为 a=1.979,b=–0.002719,c=–0.1697,d=–0.06942。
3)根据退化模型构建系统的状态转移方差和测量方程:

4)模型参数更新。预测起点之前的数据为训练集,采用RP-UPF算法实现模型参数的更新直至迭代到预测起点,得到的模型即为最终的锂离子电池容量退化模型。
5)计算RUL及其不确定性表达。通过获得的容量退化模型外推可以获得容量的预测值,当容量退化到失效阈值时经过的周期数即为当前电池的RUL。将预测起点处的每个粒子代入模型,外推可以获得每个粒子对应的RUL,采用直方图画出所有RUL的分布得到预测结果的概率分布。
3 实验结果对比分析
本文采用B0006、B0007和B0018的数据用于实验验证分析,具体实验步骤如下:
1)预测起点设置为T=60和T=80,采用PF算法、UPF算法和RP-UPF算法实现B0006的RUL预测。
2)设置预测起点为T=60、T=70和T=100,采用PF算法、UPF算法和RP-UPF算法实现B0007的RUL预测,其中T=60时RUL预测的相关结果如图2所示。

图2 T=60时B0007的预测结果
3)设置预测起点为T=75,采用PF算法、UPF算法和RP-UPF算法实现B0018的RUL预测。
4)归纳总结所有的预测结果,结果如表2所示。其中RMSE代表所有粒子预测的RUL的均方根误差,运行时间代表程序执行时间,AE代表预测的RUL与实际RUL的绝对误差。

表2 预测结果
5)进行100次重复实验并计算预测结果的均值,结果如表3所示。

表3 100次重复实验结果
从图2(a)可以看出,在参数更新阶段,随着更新次数的不断增加,采用RP-UPF算法获得的估计值与实际值的绝对误差小于采用UPF算法和PF算法获得的绝对误差,表明本文提出的RP-UPF算法相比于UPF算法和PF算法具有更好的数据跟踪能力。从图2(d)可以看出,RUL的分布大致为正态分布,符合预测实际。对比表2中T=60时B0007的预测结果,采用RP-UPF算法得到的AE比采用UPF算法获得的AE减小了6个周期,比PF算法的AE减小了17个周期;对比分析其他预测起点的预测结果,也可以看出采用RP-UPF算法得到的AE最小,这表明提出的算法预测精度更高;观察相同预测起点下不同算法的运行时间,可以发现PF算法的运行时间最小,UPF算法和RP-UPF算法的运行时间较长但两者相差不大,这表明本文提出的随机扰动重采样算法在提高粒子多样性的同时不会明显增加算法的运行时间;然后观察相同预测起点下3种算法预测的RUL的RMSE,可以发现PF算法的RMSE值最小,RP-UPF算法大部分的RMSE值最大,这表明本文提出的改进办法可以有效增加粒子的多样性。观察B0006在T=80处预测结果的AE发现,基于RP-UPF的锂离子电池RUL预测的预测效果不理想,这主要是由于在T=80时B0006存在十分明显的容量再生现象。容量再生现象表现为下一周期测得的容量高于上一周期,并且在容量再生后的一段时间出现加速退化过程。该现象会增加锂离子电池的寿命,因此当预测起点接近T=80时预测效果受到了较大影响,这也是后期需要重点解决的问题。对比分析不同电池、不同预测起点,采用3种方法得到的AE,可以发现在基于RPUPF的方法的AE变化范围为7个周期,而基于UPF的方法的AE变化范围为8个周期,基于PF方法的AE变化范围为16个周期,这表明提出的方法在不同的电池和不同的预测起点中预测结果比较稳定。采用上述分析方法分析表3,可以发现表2的结论与表3的结果一致。
4 结束语
1)本文提出了随机扰动重采样算法,然后采用UKF算法和随机扰动重采样算法改进PF算法,提出了随机扰动无迹粒子滤波算法。
2)采用双指数经验模型和RP-UPF算法构建了基于RP-UPF的锂离子电池RUL预测方法并实现了锂离子电池RUL预测,采用NASA的数据集验证实验,并对实验结果进行了对比分析。
3)对比分析了基于RP-UPF、基于UPF和基于PF的锂离子电池RUL预测方法的预测结果的绝对误差、RMSE、运行时间,表明本文提出的随机扰动重采样算法在提高粒子多样性的同时不会明显增加算法的复杂度,同时基于RP-UPF的锂离子电池RUL预测方法与基于UPF的方法相比,预测结果的AE最多减小了6个周期,AE的变化范围减小了1个周期;与基于PF的方法相比,预测结果的AE最多减小了17个周期,AE的变化范围减小了9个周期。
