中间支承输流管道自由振动的有限元分析

随岁寒，孟 华，段闪闪，李 成

中间支承输流管道自由振动的有限元分析

*随岁寒1，孟 华1，段闪闪1，李 成2

（1. 商丘工学院机械工程学院，河南，商丘 476000；2. 苏州大学轨道交通学院，江苏，苏州 215131）

基于Euler梁模型研究中间支承输流管道的动力学特性。首先，利用虚功原理，建立系统动力学有限元方程。然后，分析了支承刚度、流体离心力、预应力等因素对管道振动的影响。结果表明：支承刚度对管道系统动力学特性有重要影响，管路设计时须着重考虑；揭示了流体离心力是造成固有频率随流速增大而降低的根本原因；流体科氏力对各阶固有频率影响较小；预应力对振动的影响不可忽略，尤其是第一阶固有振动；

中间支承，输流管道，自由振动，临界速度，有限元法

0 引言

输流管道系统广泛应用于航空航天和石油化工等领域，研究其振动和稳定性具有重要价值。在开展相关研究中，多种数值方法得到应用，例如伽辽金法[1-4]、格林函数法[5]、微分求积法[6-7]、微分变换法[8-9]、动态刚度矩阵法[10]和有限元法[11-12]。其中，文献[11]研究随机弹性模量、密度和流速对管道特征值和动力响应的影响。文献[12]求解了弹性地基上输流管道的固有频率和临界速度。另外，工程中设计管路系统时往往通过设置中间支撑来增加系统稳定性，且这一支承通常具有一定弹性，对其建模不同于弹性地基支承和刚性支承，需要特殊处理。目前这方面的研究还比较少，由于弹簧内储存的势能属于系统势能，因此本研究将支承刚度整合到管道系统的整体刚度矩阵从而建立其动力学有限元方程。需要指出的是，当中间无支承或者支承弹性较小时，输流管道可视为单跨管道，而当支承刚度大到一定程度则管道系统的振动特性趋于接近多跨管道。部分学者在研究输流管道问题时加入了中间支承这一因素，如荆洪英等[12]研究了一端固定具有中间支承悬臂输流管道的临界流速及其稳定性。邓家全[13]全面探讨了多跨管道的支承数目和支承位置等参数对多跨功能梯度输流管道自由振动和稳定性的影响，但研究的是中间刚性支承这一特例。

另外，管道系统固有频率随流体速度的增大而降低，这一结论作为学术界共识而广为人知。理论分析认为造成这一现象的原因是流体的离心力和科氏力的共同作用，然而尚无相关文献揭示离心力和科氏力的主次关系。已有文献多采用哈密顿原理建立弹性体系的动力学方程，例如文献[12-13]。我们采用虚功原理，其优势在于利用虚功原理便于明确流体各加速度的物理含义，进而利于单独分析各加速度对系统振动特性的影响。

由于工程实际中的安装以及环境温度变化等因素都可能造成管道产生轴向力，本文最后还探讨了预应力对固有频率的影响。

1 数学模型

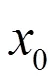
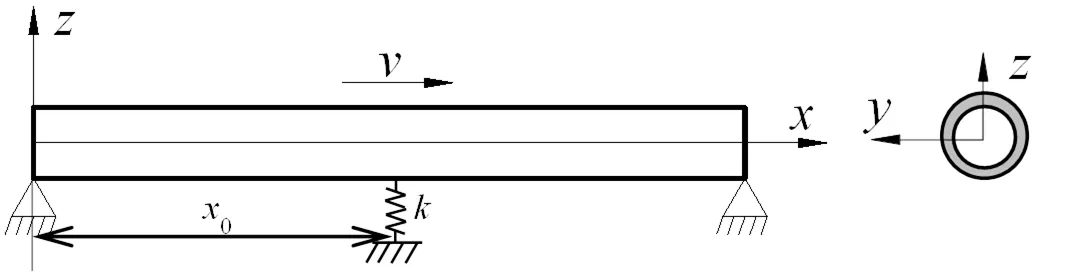
图1 输流管道示意图

由于输流管道为细长结构，因此可将其简化为Euler梁模型，则管道单元的应变能变分为

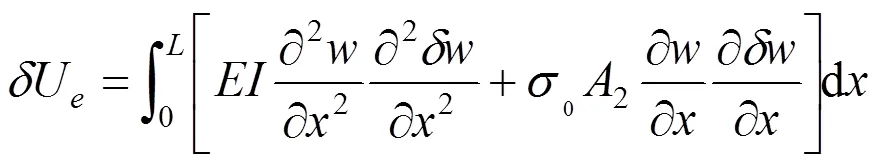
流体质点的横向加速度可按照加速度合成定理得到，

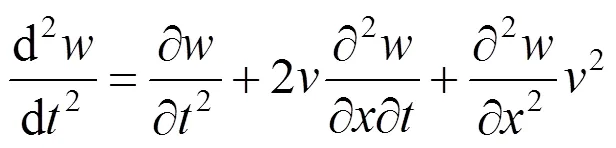
其中各项物理意义如下

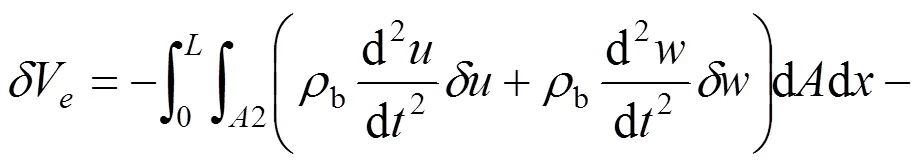
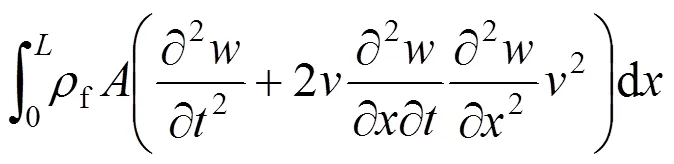
将（1）式和（3）式代入如下虚功原理表达式

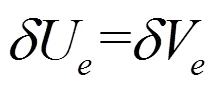
经分步积分后得到

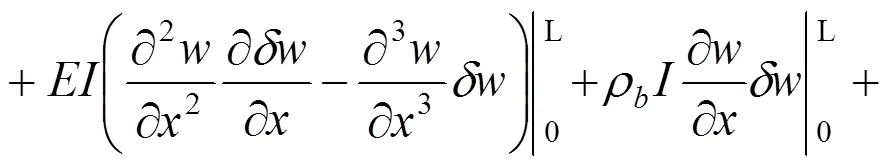
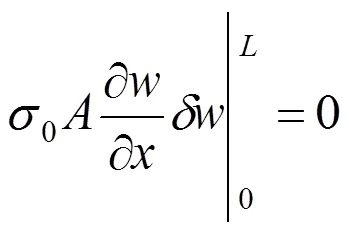
采用Hermit形函数，如下

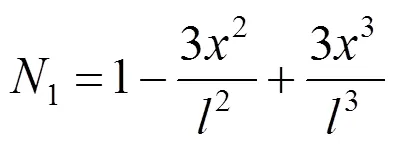
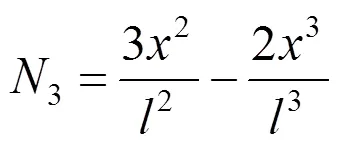
则管道单元横向位移可表达为

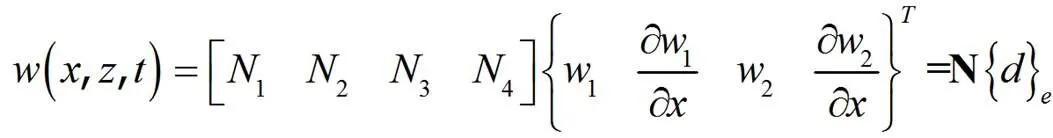
将（7）式代入（5）式得到管道的单元有限元方程

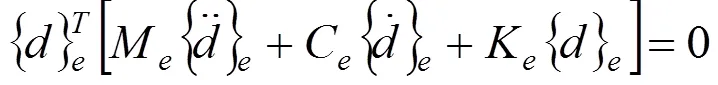
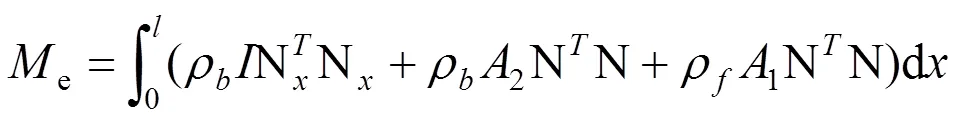
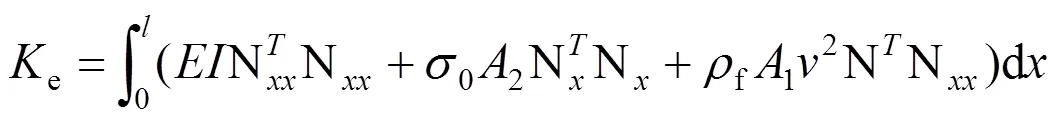
因节点位移向量{}的任意性，从而由（8）式得到输流管道单元的平衡方程

对（11）式的单元矩阵经组装后得到输流管道系统在不考虑支承条件下自由振动的有限元方程

其中、和分别为整体质量阵、整体陀螺矩阵和整体刚度矩阵。

由于支承的弹性势能属于系统整体势能，因此须将支承刚度矩阵统一到整体刚度矩阵。支承弹性势能变分为

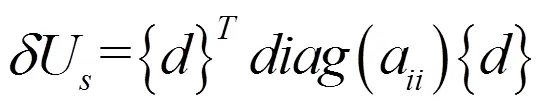
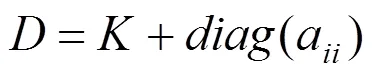
将（13）式的替换为，得到考虑支承条件下自由振动的有限元方程

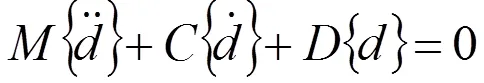
2 数值结果与讨论

采用参数为弹性模量E=210 GPa，密度ρ = 7850 kg/m3，流体密度ρ=800 kg / m3。管道程度L=8 m，支承点坐标x0=L/2，圆管内壁半径R1=0.1825 mm，外壁半径R2=0.1885m。

（16）式结合两边简支的边界条件，求解得各阶固有频率。图2给出了前三阶固有频率与流体速度的关系，输流管道系统的振动特性表现为流体平均速度越大，固有频率越小。图2中浅色线和粗黑色线分别为忽略流体离心力和忽略科氏力两种情况下对应的频率曲线。当速度较小时，离心力和科氏力都很小，因此三条曲线基本重合。但是当速度增大到一定数值比如100 m/s时，离心力和科氏力便不可忽略，三条曲线开始发散，粗黑色线比浅色线偏离实际值更多。这说明，离心力的存在是造成固有频率随流速增大而减小的主要原因，离心力的影响远大于科氏力。需要指出的是，在第一阶固有频率减小到零时系统失稳，在该点对应的流体速度称为临界速度。

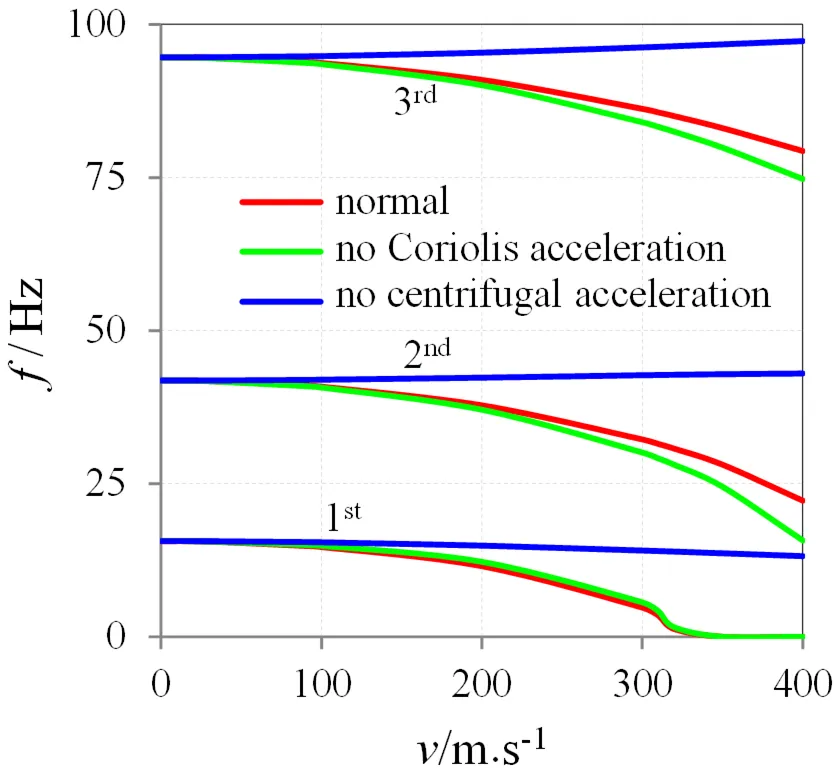
图2 固有阶频率随流体速度的变化

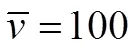
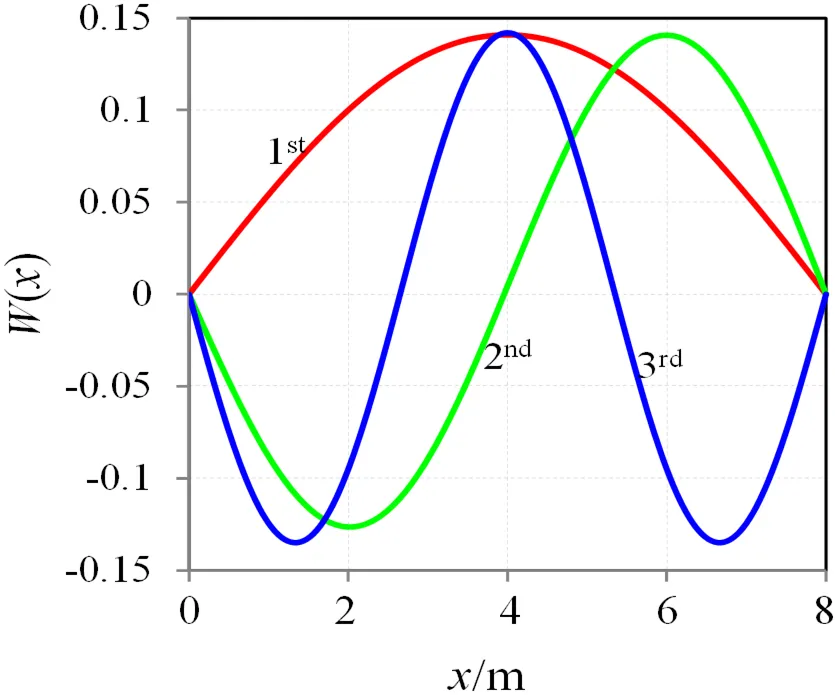
图3 管道模态函数（k=3×106 N·m-1）

图4（a）给出了支承刚度从0到100×106N·m-1变化时，前三阶固有频率的变化情况，支承刚度从0增大到20×106N·m-1的过程中，前三阶频率增大比例分别为219.43%、0.45%、5.53%。可见支承刚度对第一阶频率影响最大，对第二阶固有频率几乎没有影响，对第三阶固有频率影响相对较小，产生这一现象的根源可以从图3前三阶模态函数找到原因，即：第一阶和第三阶固有频率的振动始终受到支承的约束，随着频率的升高系统的振动幅值会逐步衰减，因此第三阶固有频率相对第一阶固有频率受到支承的影响较小；而第二阶模态在管道跨度中点处的位移始终为零，因此第二阶固有频率不受支承刚度影响。

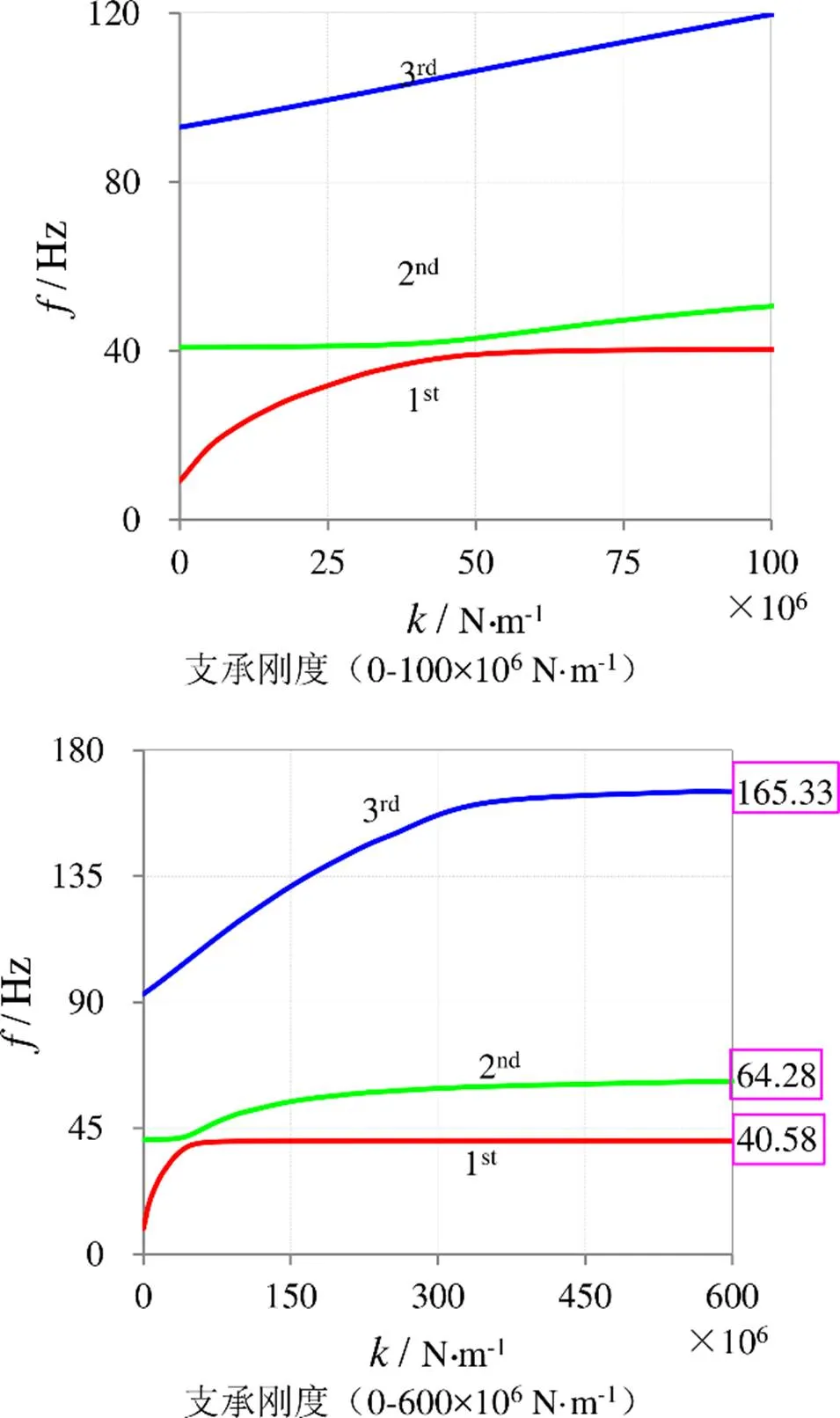
图4 固有频率随支承刚度的变化

继续增大支承刚度到50×106N·m-1时，第一阶固有频率等于支承刚度为零时的第二阶固有频率，并且第二阶固有频率由该点开始随支承刚度的增大而增大。为解释这一现象，图5和图6分别给出了=40×106N·m-1和=+∞ N·m-1（双跨管道）时的前三阶模态函数。对比图3、图5和图6可以发现，单跨管道的第二阶模态与双跨管道的第一阶模态类似，因此，当支承的刚度增大到一定数值比如40×106N·m-1时，输流管道的前三阶模态处于单跨管道和双跨管道的过渡状态。随着支承刚度的增大，单跨管道逐渐向双跨管道过渡。

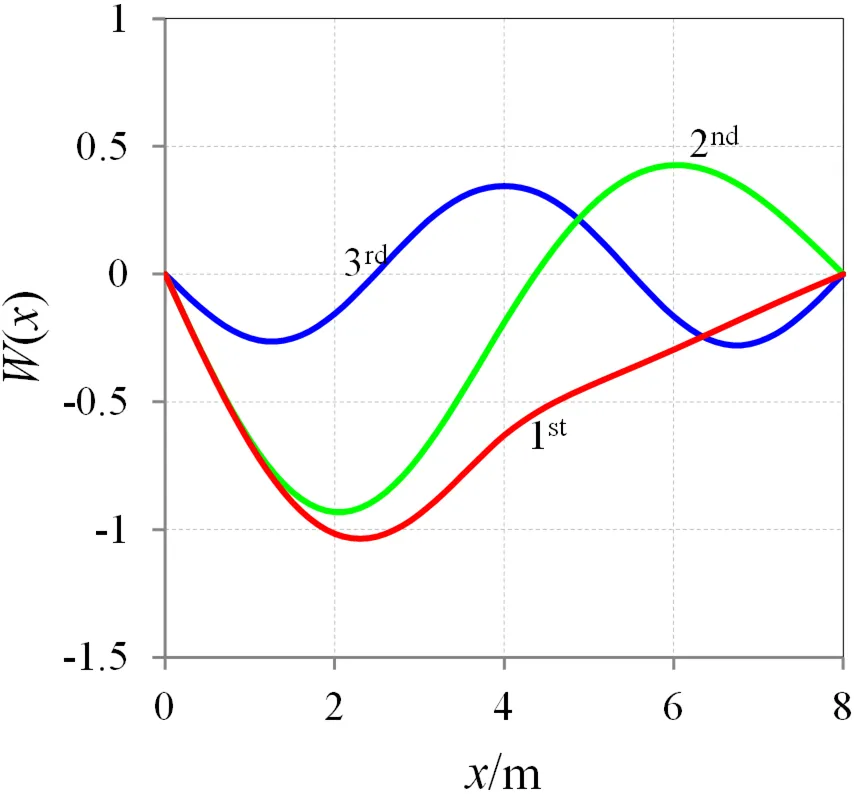
图5 管道模态函数（k=40×106 N·m-1）

图6 双跨管道模态函数（k=+∞ N·m-1）

图4（b）给出了支承刚度增大到600×106N·m-1时，前三阶固有频率分别收敛到40.58 Hz、64.28 Hz和165.33 Hz，此时支承接近刚性支承，这三个频率代表双跨管道的前三阶固有频率。

图7给出了前三阶临界速度与支承刚度的关系，由图可见，支承刚度增大过程中，第一阶临界速度随着支承刚度增大而增大；第二阶临界速度不变；第三临界速度也随着支承刚度增大而增大。原因如前所述，支承刚度在增大的过程中管道系统实际上等于是从单跨管道转化为双跨管道。由图7（b）可见前三阶临界速度收敛于双跨管道的前三阶临界速度，即431.66 m/s、615.64m/s和863.26m/s.

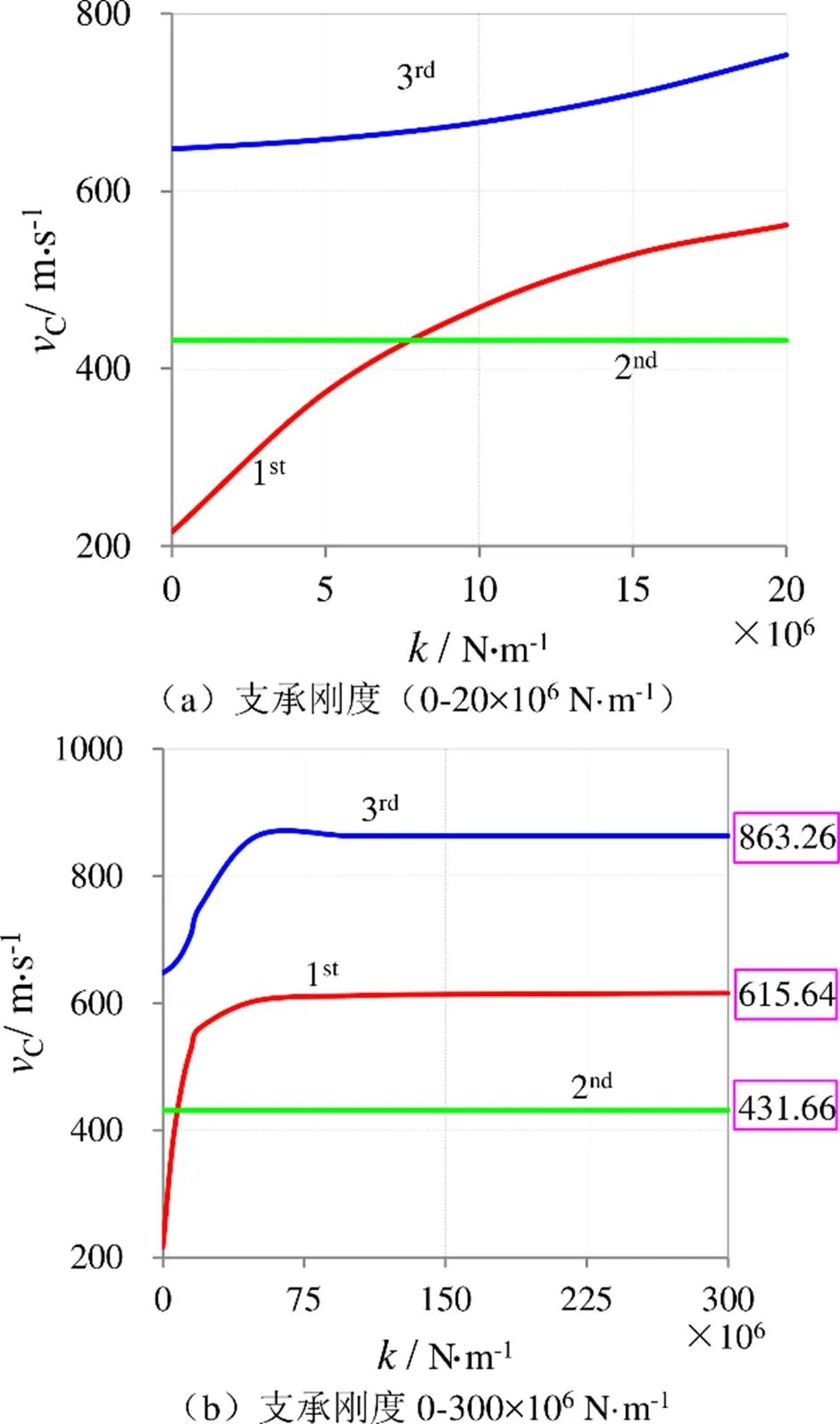
图7 临界速度随支承刚度的变化

表1给出了预应力对前三阶固有频率的影响，在预应力从-50 MPa增大到50 MPa的过程中，前三阶固有频率均增大，增大比率为4.63%、2.36%和1.00%。由于工程中预应力不可避免，因此在研究输流管道振动，尤其低阶振动频率时，预应力因素须予考虑。

表1 固有频率随预应力的变化

Table 1 Natural frequencies vs. pre-stress

预应力/MPa第1阶固有频率/Hz第2阶固有频率/Hz第3阶固有频率/Hz -5014.3240.3793.23 014.6540.8593.70 5014.9841.3294.17

3 结论

采用Euler梁模型模拟细长管道，利用虚功原理建立了中间支承输流管道的动力学有限元方程。数值求解了前三阶固有频率及其模态函数，随后探讨了流体速度、支承刚度和预应力对系统自由振动的影响。着重分析了支承刚度、流体离心力和预应力对固有频率和临界速度的影响。结论如下：

1）随着支承的刚度增大，各阶有阶固有频率和临界速度逐渐增大并收敛于双跨管道的前三阶固有频率和临界速度；

2）在流体离心力和科氏力共同作用下，各阶固有频率随流体速度的增大而降低，离心力起主导作用；

3）各阶固有频率随着预应力的增大而增大，其中第一阶固有频率受预应力影响最大。

[1] Sazesh S, Shams S. Vibration analysis of cantilever pipe conveying fluid under distributed random excitation[J]. Journal of Fluids and Structures, 2019, 87:84-101.

[2] 许锋, 郭长青, 黄建红. 弹性支承输流管道在分布随从力作用下的稳定性[J]. 工程力学, 2014, 31(7):234-238.

[3] Bahaadini R, Hosseini M, Jamalpoor A. Nonlocal and surface effects on the flutter instability of cantilevered nanotubes conveying fluid subjected to follower forces[J]. Physica B Condensed Matter, 2017, 509:55-61.

[4] Gu Z, Bai C, Zhang H. Stochastic finite-element modeling and dynamic characteristics analysis of pipe-conveying fluid[J]. Journal of Vibration Engineering & Technologies, 2019:9.

[5] Li Y D, Yang Y R. Forced vibration of pipe conveying fluid by the Green Function Method[J]. Archive of Applied Mechanics, 2014, 84(12):1811-1823.

[6] Wang L, Hong Y, Dai H, et al. Natural frequency and stability tuning of cantilevered CNTs conveying fluid in magnetic field[J]. ActaMechanicaSolidaSinica , 2016, 29(6):567 - 576 .

[7] Tang Y, Yang T. Bi-directional functionally graded nanotubes: fluid conveying dynamics[J]. International Journal of Applied Mechanics, 2018,10(4):1850041（1-22）.

[8] Ni Q, Zhang Z L, Wang L.Application of the Differential transformation method to vibration analysis of pipes conveying fluid[J]. Applied Mathematicsand Computation, 2020, 217: 7028-7038.

[9] 李明,周攀峰,郑慧明. 多场作用下输流单层碳纳米管的动力学特性[J]. 固体力学学报, 2017, 38(5):426-432.

[10] Li Y, Li Y, Akbar N. Analysis of Vibration of the Euler-Bernoulli Pipe conveying fluid by dynamic stiffness method and transfer matrix[J]. Journal of Applied Mathematics and Physics, 2020, 8(1):172-183.

[11] Li B, Wang Z, Jing L. Dynamic response of pipe conveying fluid with lateral moving supports[J]. shock and vibration, 2018(10):3295787.1-3295787.17.

[12] Dahmane M, Samir Z, Mawhoub S, et al. Free vibration induced by internal flow in cantilevered pipeunder different parameters[J]. International Journal of Advanced Scientific and Technical Research, 2020, 5(10): 1-12.

[13] 邓家全. 多跨功能梯度输流管道流固耦合动力学特性与计算方法研究[D]. 西安:西北工业大学.2018

FINITE ELEMENT ANALYSIS ON FREE VIBRATION OF FLUID-CONVEYING PIPES WITH INTERMEDIATE SUPPORT

SUI Sui-han1, MENG Hua1, DUAN Shan-shan1, LI Cheng2

（1. School of Mechanical Engineering, Shangqiu Institute of Technology, Shangqiu, Henan 476000, China;2. School of Rail Transportation, Soochow University, Suzhou, Jiangsu 215131, China）

The dynamic characteristics of fluid-conveying pipes with intermediate support was studied based on Euler beam model. Firstly, utilizing virtual work principle, the finite element dynamic equation of pipe system was established. Then, the influence of stiffness of support, fluid centrifugal force and pre-stress on pipe vibration was analyzed. The results showed that the stiffness of support had a significant effect on the dynamic characteristics of the pipe system, which should be taken into account serious lyin pipe design. It suggested that the centrifugal force of fluid was the root cause of the fact that natural frequencies decrease with the increase of flow velocity. The fluid Coriolis force had little effect on the natural frequencies of each order. The influence of pre-stress on vibration couldn’t be ignored, especially the first natural vibration.

intermediate support; fluid-conveying-pipe; free vibration; critical velocity; finite element method

O327

A

10.3669/j.issn.1674-8085.2021.03.015

1674-8085（2021）03-0085-06

2021-02-28；

2021-03-27

国家自然科学基金项目(11972240)

*随岁寒(1988-)，男，河南商丘人，讲师，硕士，主要从事计算力学研究（E-mail: suisuihan@163.com）；

孟 华(1988-），女，河南商丘人，讲师，硕士，主要从事转子动力学研究(E-mail:463310334@qq.com）；

段闪闪(1989-),女，河南商丘人，讲师，硕士，主要从事机械有限元分析研究(E-mail:1061476212@qq.com);

李 成(1983-)，男，江苏徐州人，教授，博士，主要从事微纳米结构力学研究(E-mail: licheng@suda.edu.cn