具有二阶扰动和疫苗接种的随机霍乱传染病模型的平稳分布

2021-09-10张艳敏刘明鼎

井冈山大学学报(自然科学版) 2021年3期

关键词：分布图二阶数学模型

张艳敏，王丹，刘明鼎

*张艳敏，王丹，刘明鼎

（青岛理工大学琴岛学院基础教学部，山东，青岛 266106）

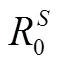
随机霍乱传染病模型；二阶扰动；疫苗接种；平稳分布；Lyapunov函数

0 引言

霍乱是一种由霍乱弧菌引起的急性腹泻性传染病[1]。感染者会出现水样腹泻、呕吐和严重脱水，如果不及时治疗，数小时内就会死亡[1]。据统计，全世界每年有130万至400万人感染霍乱，另有2.1万至14.3万人因霍乱死亡[2]。疫苗作为控制传染病的有效手段，已被广泛应用到研究霍乱传染的数学模型当中[3-5]。近年来为了分析霍乱传染的动力学性质，并为有效预防和控制霍乱的传播提供参考，学者们给出了众多确定性霍乱数学模型[6-10]，并对模型的性质进行研究。在这些成果中，有学者研究了模型的稳定性问题，有学者研究了模型的最优控制问题，还有学者研究了具有疫苗接种下的霍乱控制问题，这些研究成果被广泛应用到实际问题解决当中。尤其在2020年全球爆发新型冠状病毒，对传染病的有效控制研究吸引了学者们更广泛的关注。因此通过数学模型研究霍乱传染病的有效控制问题不仅具有理论意义，更具有现实意义。

在文献[4]中，Xu等提出了如下具有疫苗接种的霍乱传染病模型：

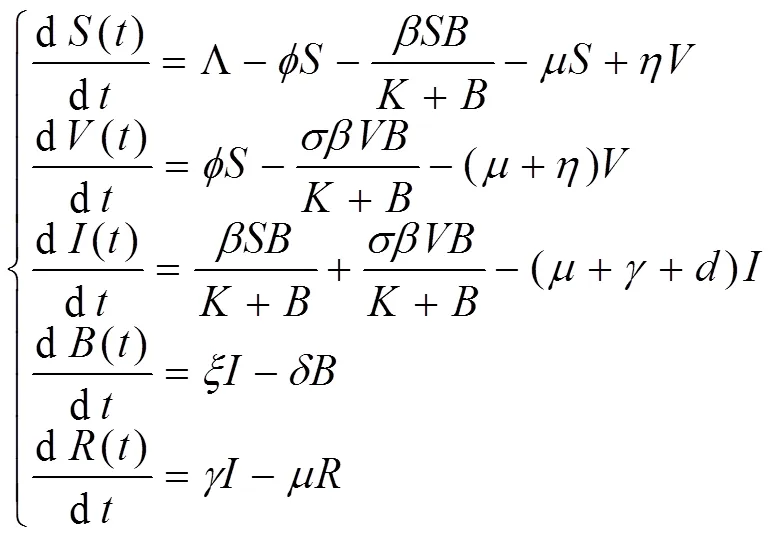
然而在现实中，任何传染病模型都不可避免的受到环境噪声的干扰，在模型中加入随机干扰是必要的，且更符合实际情况。因此研究霍乱模型式（1）加入随机干扰项更能解决实际问题。近些年，也有很多学者研究了随机传染病模型的动力学行为[11-14]。在这些随机模型中，多数研究的是具有线性干扰项。其中ZHANG等[1]研究了系统式（1）的如下线性随机霍乱传染病模型：

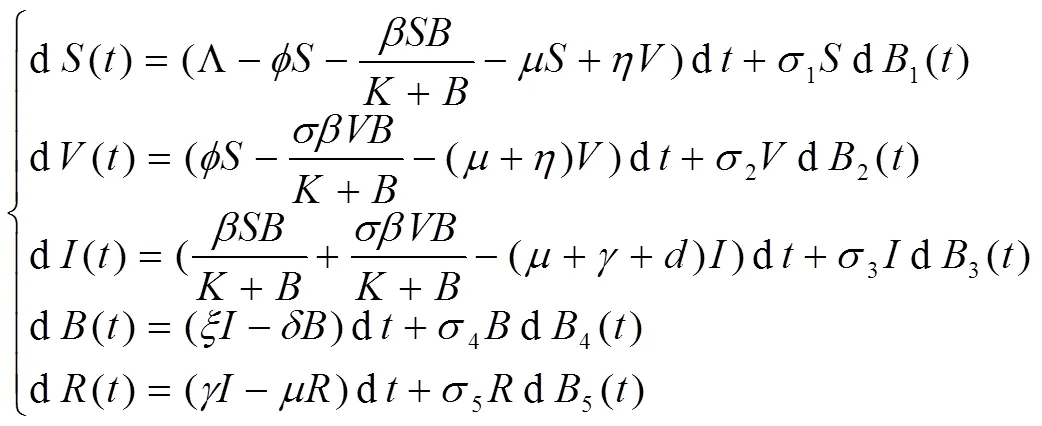
引理1[1]对任意的初始条件

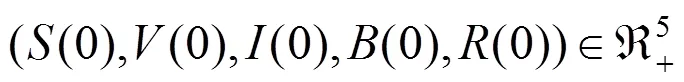
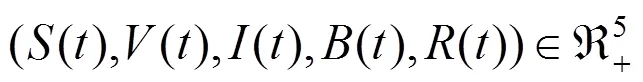
引理2[1]对任意的初始条件

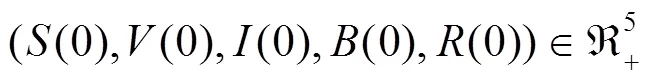
然而在现实状态中，随机传染病模型的动力学行为会受到各种复杂噪声的干扰。受文献[14]的启发，传染病模型受到非线性干扰比线性干扰更符合实际情况。然而具有二阶扰动的随机传染病模型的相关的研究成果相对较少，因此本文将研究如下二阶扰动的随机霍乱传染病模型的平稳分布：

正平衡态的稳定性是生物数学模型动力学性质的重要研究内容。然而，大多数随机模型没有传统的正平衡态。因此，随机生物数学模型的平稳分布（随机正平衡态）一直受到广泛关注。此外式（3）受到二阶白噪声的干扰，这也增加了分析的难度。本文将致力于证明模型（3）平稳分布的存在性。

1 预备知识

引理3 对任意的初始条件

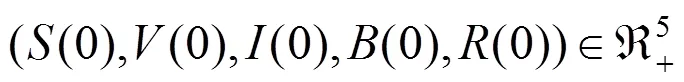
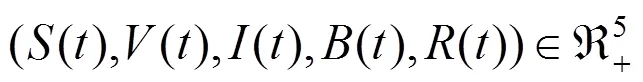
引理3的证明方法是标准的，与文献[15]引理1的证明方法与过程几乎是一致的。这里省去证明过程。

引理4

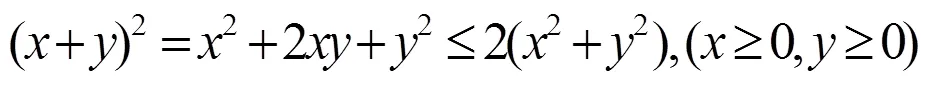
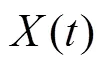
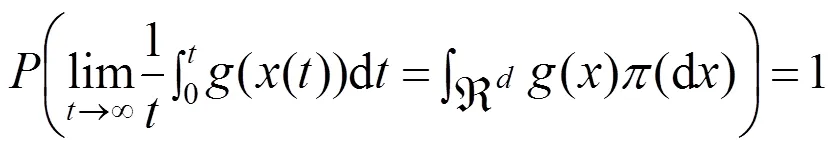
为了清晰证明过程，给出如下记号：

2 平稳分布

定义1[1]对于维随机微分方程

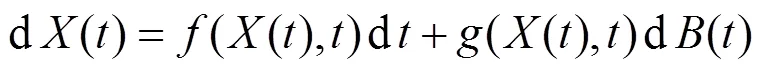
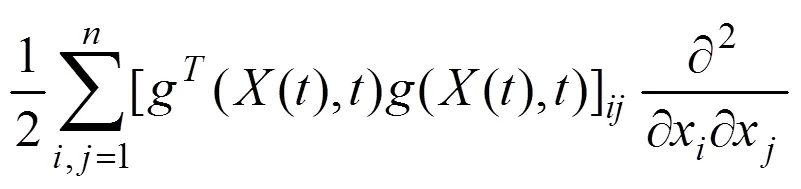
定理1对任意的初始条件

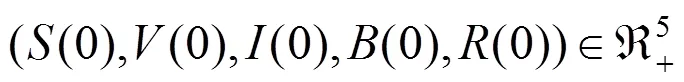
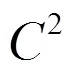
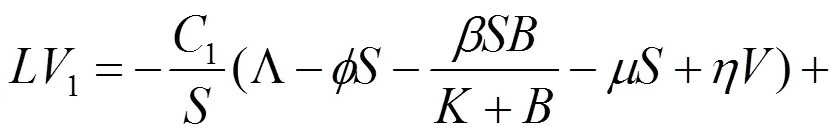
取

则可以得到

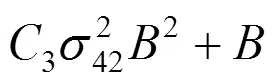
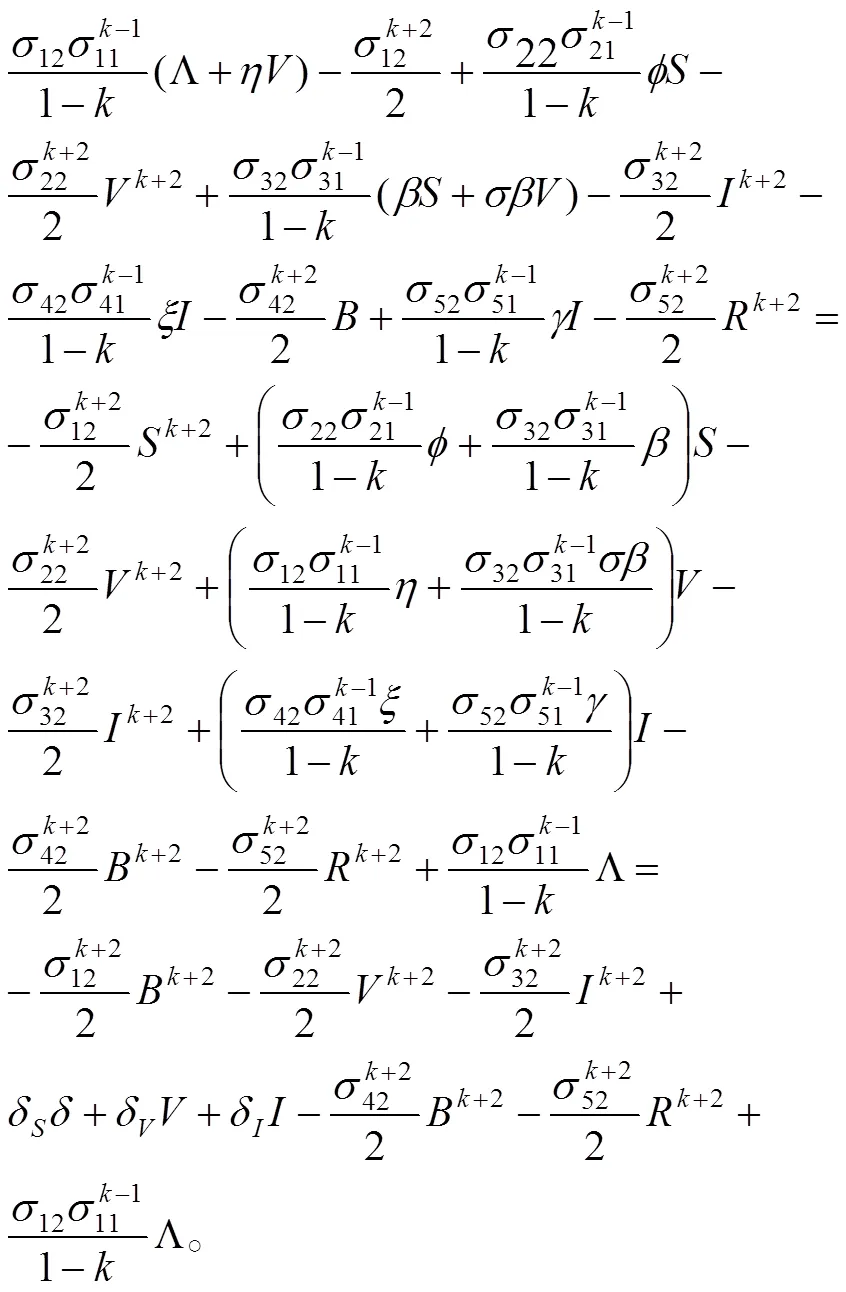
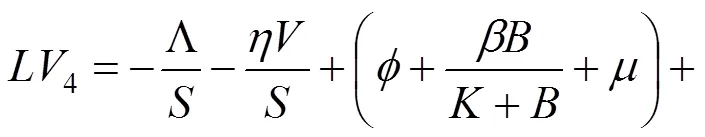
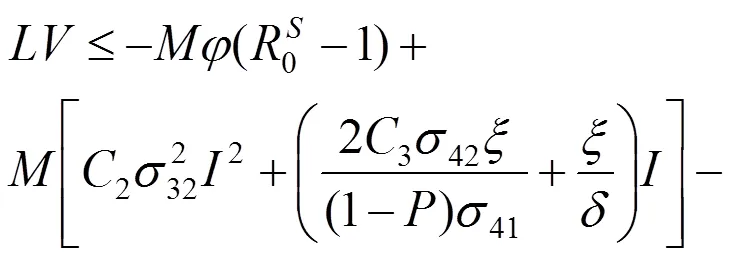
其中

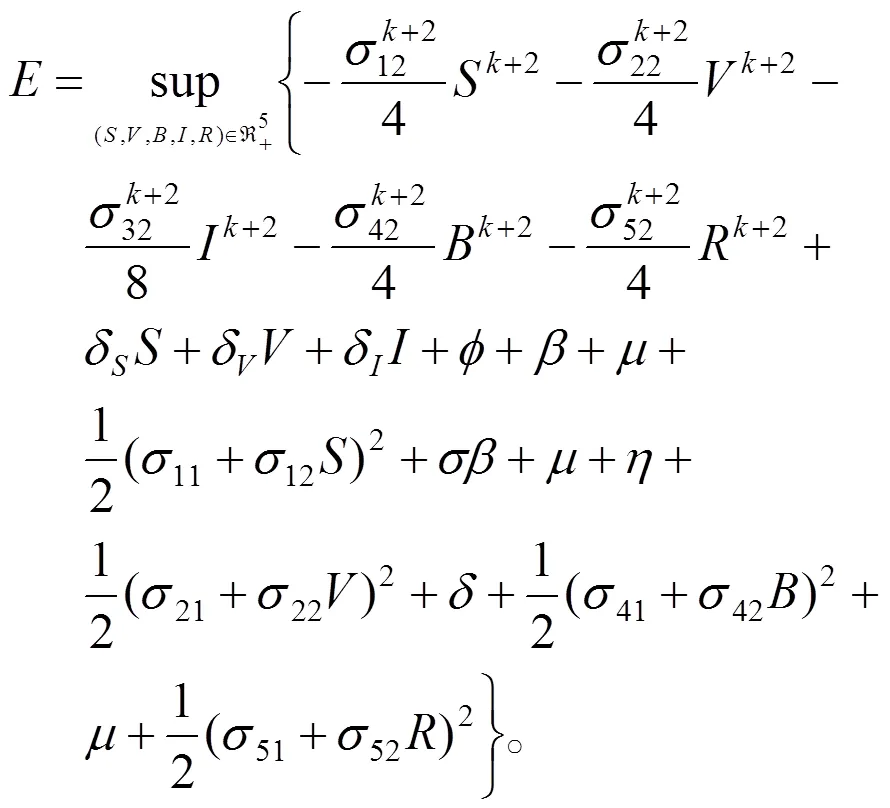
定义有界闭集：

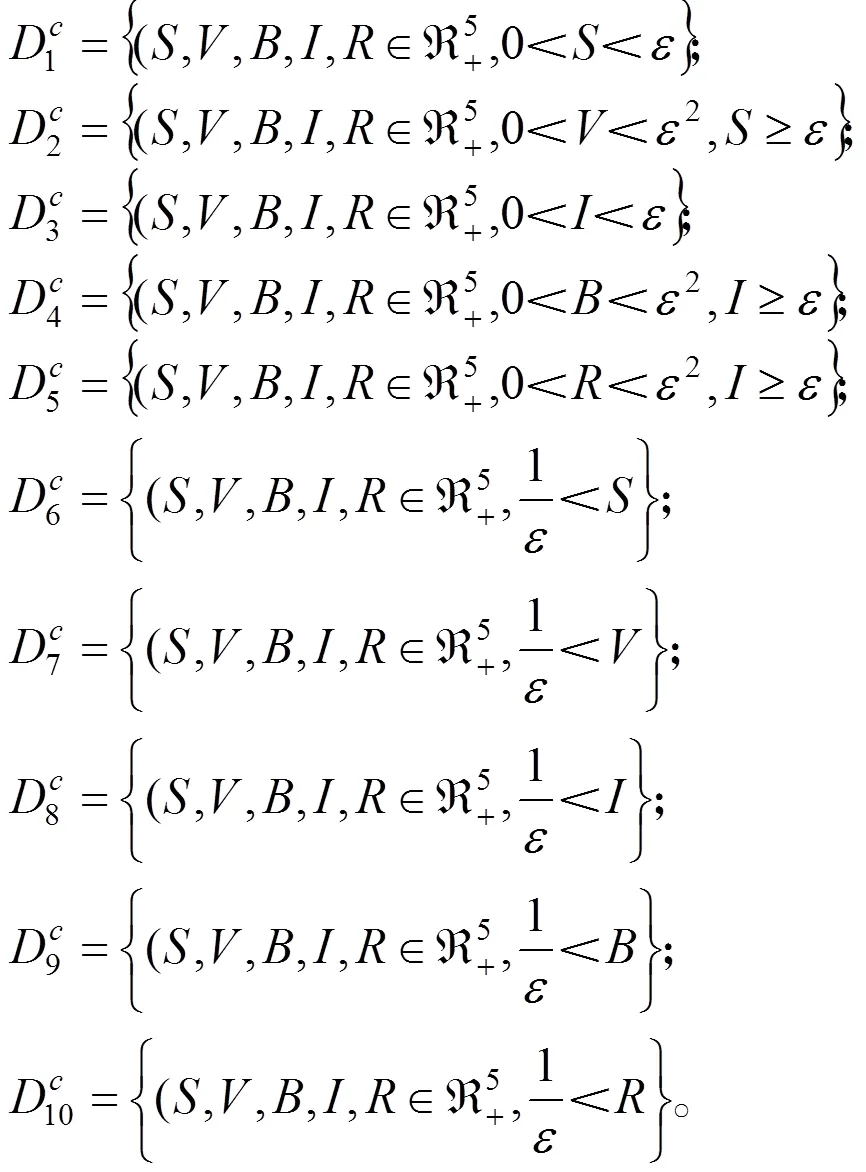
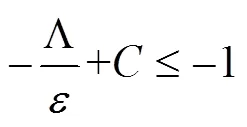
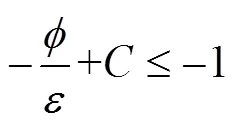
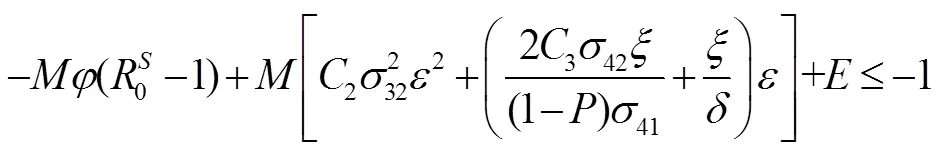
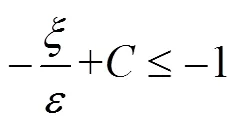
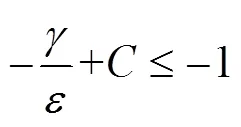
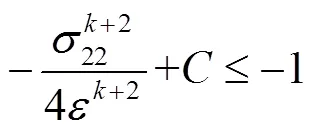
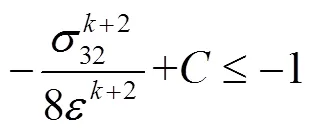
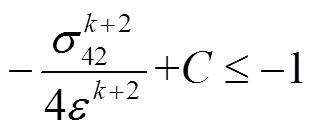
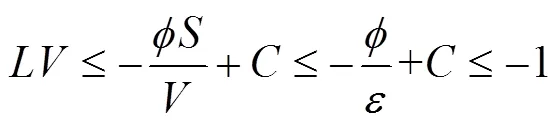
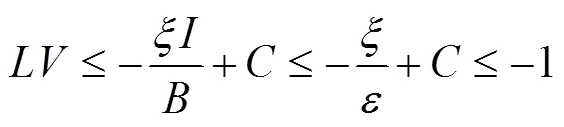
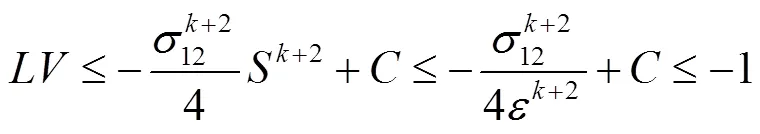
3 数值模拟

将通过数值模拟验证本文的理论结果。所使用的数据来源于文献[4,17-18]，具体数值见表1。

表1 模型3的系数值

Table 1 Parameter values for the model（3）

系数数值来源文献 0.1/day[4] 0.01/day[4] 0.8/day[17] Kcells/ml[17]assumed 0.005/day[4] 2.2493×10-5day[18] 10%[4] 0.004/day[17] 0.015/day[17] 100 cells/ml-per day[18] 0.012/day[18]

依据Milstein[19]给出的方法，以及文献[20]，构造式（3）的离散方程如下：

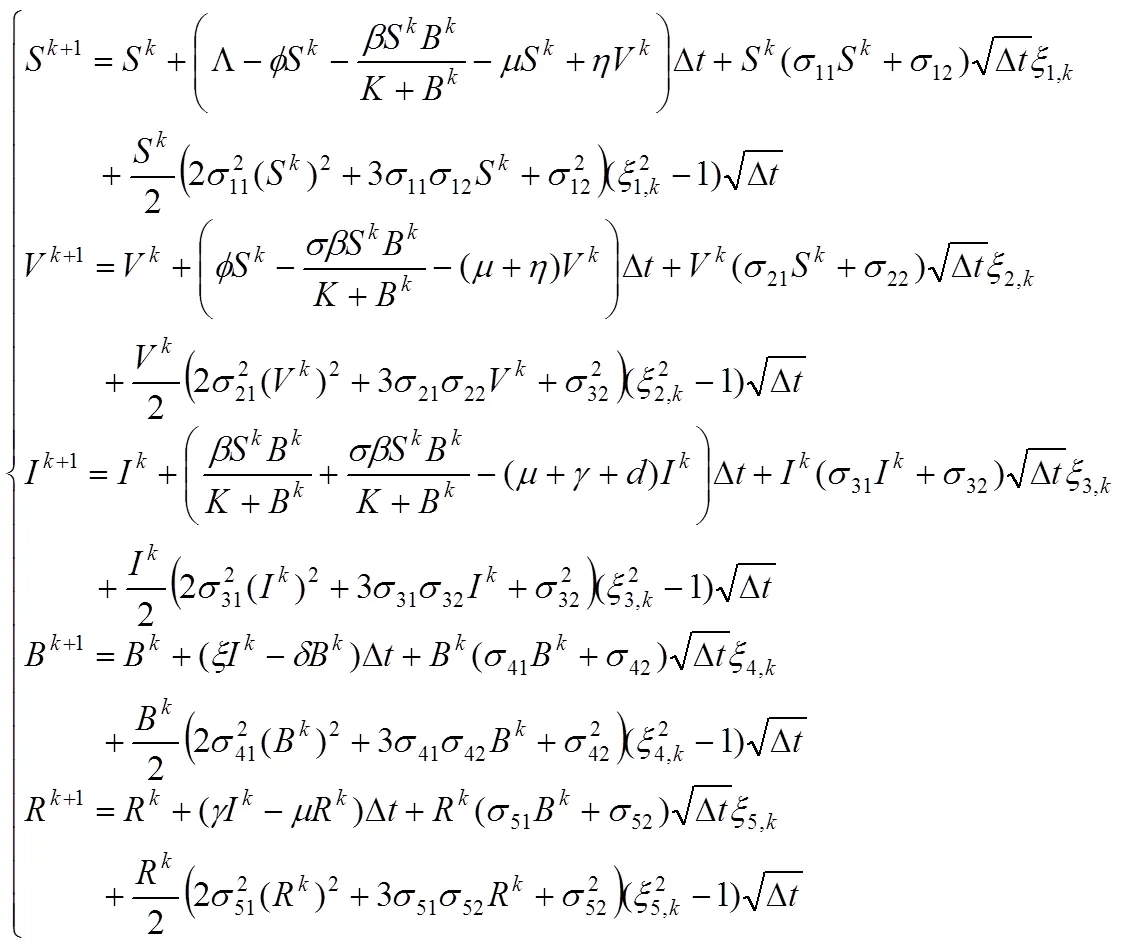
图1 分布图

Fig.1 Density of

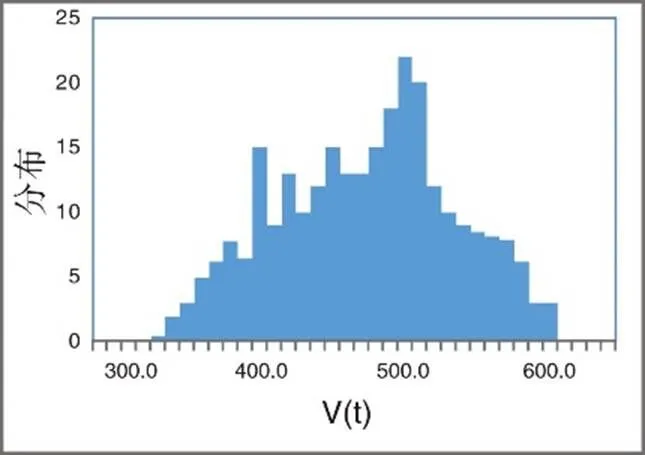
图2 分布图

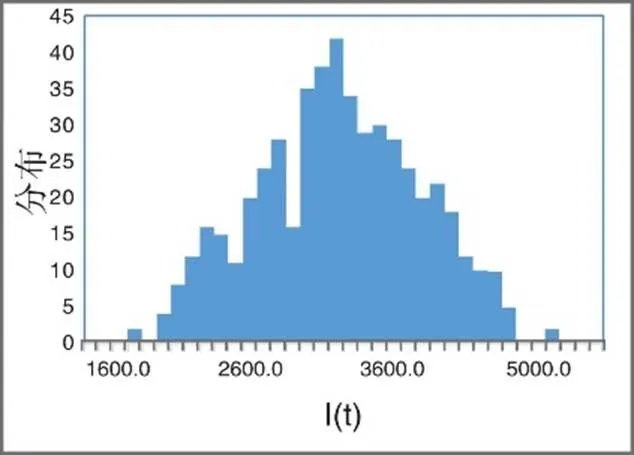
图3 分布图

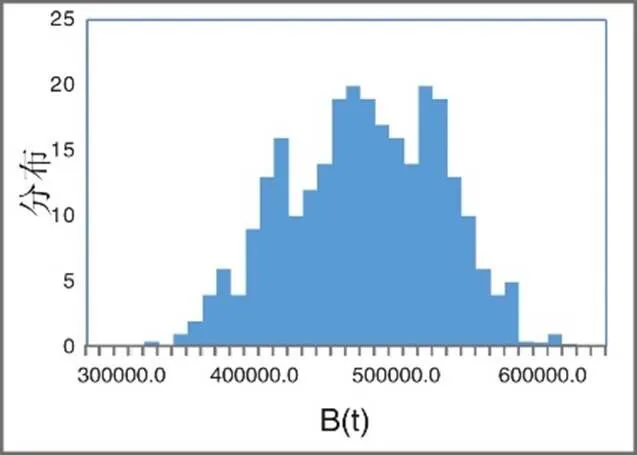
图4 分布图

图5 分布图

4 结论

[1] Zhang X H, Hao P. Stationary distribution of a stochastic cholera epidemic model with vaccination under regime switching[J]. Applied Mathematics Letters,2020(102):1-7.

[2] Codeco C T. Endemic and epidemic dynamics of cholera : the role of the aquatic reservoir[J]. BMC Infect. Dis., 2001(1):1-14.

[3] Tien J H, Earn D J D. Multiple transmission pathways and disease dynamics in a waterborne pathogen model[J].Bull. Math. Biol. ,2010 (72) :1506-1533.

[4] Tian X, Xu R, Lin J. Mathematical analysis of a cholera infection model with vaccination strategy[J].Appl. Math. Comput.,2019 (361) :517-535.

[5] Liu M, Deng M L. Analysis of a stochastic hybrid Population model with Allee effect[J].Applied Mathematics and Computation,2020,364:124582.

[6] 佘高烊.一类霍乱模型行波解的存在性[D].哈尔滨：哈尔滨工程大学,2019.

[7] 杨炜明,廖书.含有预防接种的霍乱时滞模型的稳定性和hopf分支分析[J].应用数学学报,2018,41(6):735-749.

[8] 吴青青. 一类非均质空间中的霍乱扩散模型的动力学行为[D].扬州: 扬州大学,2018.

[9] 杜争光.具有Holling Ⅳ型功能反应的分数阶捕食者-食饵模型的动力学分析[J].井冈山大学学报:自然科学版,2019,40(3):9-13,23.

[10] 廖书,杨炜明.含有预防接种的霍乱最优控制模型分析[J].系统科学与数学,2016,36(12):2257-2271.

[11] 王来全,夏米西努尔·阿布都热合曼.一类具有季节变化和周期解的随机SIR传染病模型[J].北华大学学报自然科学版,2020,21(5):568-572.

[12] 文乾英,焦建军.在随机环境中的非自治SI传染病模型的动力学分析[J].数学的实践与认识,2020, 50(11): 255- 259.

[13] 辛明振. 两类随机传染病模型的动力学行为研究[D].兰州: 兰州大学,2020.

[14] Liu Q, Jiang D Q. Stationary distribution and extinction of a stochastic SIR model with nonlinear perturbation[J]. Applied Mathematics Letters,2017(73):8-15.

[15] Has’minskii R. Stochastic stability of differential equations[M]. Alphen aan den Rijn: Sijthoff & Noordhoff, 1980.

[16] Mao X . Stochastic differential equations and applications, seconded[M]. Chichester UK: Horwood, 2008.

[17] Hartley D M, Jr J G M, Smith D L. Hyperinfectivity : A Critical Element in the Ability of V. cholerae to Cause Epidemics ? [J]. PLoS Medicine, 2006, 3(1):e7.

[18] Modnak C. A model of cholera transmission with Hyper - infectivity and its optimal vaccination control [J]. International Journal of Biomathematics, 2017,10(6):201 - 216.

[19] Higham, Desmond J. An Algorithmic Introduction to Numerical Simulation of Stochastic Differential Equations[J]. Siam Review, 2001, 43(3):525-546.

[20] Han B T, Jiang D Q, Hayat T, et al. Stationary distribution and extinction of a stochastic staged progression AIDS model with staged treatment and second-order perturbation[J]. Chaos, Solitons & Fractals, 2020: 140.

STATIONARY DISTRIBUTION OF A STOCHASTIC CHOLERA EPIDEMIC MODEL WITH SECOND-ORDER PERTURBATION AND VACCINATION

*ZHANG Yan-min, WANG Dan, LIU Ming-ding

（Qingdao University of Technology Qingdao College, Department of Basic Education, Qingdao, Shandong 266106, China）

stochastic cholera epidemic model; second-order perturbation; vaccination; stationary distribution; Lyapunov function

O211.63

10.3669/j.issn.1674-8085.2021.03.001

1674-8085（2021）03-0001-07

2021-01-24；

2021-03-10

山东省高等教育研究项目(19GDJ019); 青岛理工大学琴岛学院重点研究项目(2020001A)

*张艳敏(1981-)，女，山东东营人，副教授，硕士，主要从事微分方程理论研究(E-mail:zhym0628@163.com);

王丹(1982-)，女，山东青岛人，副教授，硕士，主要从事微分方程理论研究(E-mail:253065193@qq.com);