二维势箱函数的可视化研究

谢凯强，刘 锴，吴 坤，王茂隆，李玉洁，郑兴荣

二维势箱函数的可视化研究

谢凯强，刘 锴，吴 坤，王茂隆，李玉洁，*郑兴荣

（陇东学院电气工程学院物理系，甘肃，庆阳 745000）

运用分离变量法和数值仿真，得到了量子理论中二维势箱函数波函数及其相关特性的理论和可视化结果。结果表明：二维势箱函数的能级是量子化的；能量随着量子数的增加而增加，但势箱长度和宽度越大，能量越小。对于二维的正方势箱函数，粒子波函数的简并度为n+n-1，峰值个数为n•n，且与=0平面的交线数也为n•n；几率密度分布的极大值个数也为n•n。本文的这种推导结果和可视化结果与理论结果完全一致。通过可视化结果解决了势箱函数教学和科学研究的难题，并为用MATLAB数值计算解决同类问题提供借鉴。这对于抽象性概念的理解具有重要意义。

二维势箱函数；分离变量法；数值仿真；波函数；几率密度；能量

0 引言

势箱函数和线性谐振子、氢原子作为量子理论中最简单、最重要的模型，是学习量子力学，乃至整个量子理论的基础和入门[1-3]。势箱函数模型，指的是处于束缚态中的任何粒子, 设其一个具有理想反射壁的维空间里（一维、二维、……）不受其他任何外力作用，而使其不能穿过维壁而只能在空间内自由运动的一种量子模型[4-5]。也就是说，处于势箱函数模型中的粒子处于束缚态。势箱函数及其模型应用广泛，尤其在微观领域下，如原子核中的质子、中子的运动，原子中电子的运动，金属中电子的运动，共轭分子内电子的运动，以及原子内部电子在两个能级之间的跃迁、零点能[6-9]等。另外，势箱函数模型还是量子力学中最简单的束缚态情况，可以让初学者把握并理解量子力学的基础概念和一般性质，如量子数、简并度、几率密度和能量的分立取值等[10-15]。最后势箱函数模型还是处理某些问题有用的简化模型，如束缚粒子，其势箱就好像提供了一个无穷大的势垒。

基于数学物理思想，结合前期工作[16-17]，本文运用分离变量法和MATLAB软件的数值仿真功能[18-19]，得到了势箱函数的相关特性，包括理论结果和可视化结果。这种研究思路和方法解决了势箱函数在教学和科研上的难题。同时也为用MATLAB数值计算和仿真解决其他问题提供案例。

1 理论模型与推导

任一粒子在二维空间中运动，则它的体系满足定态薛定谔方程：

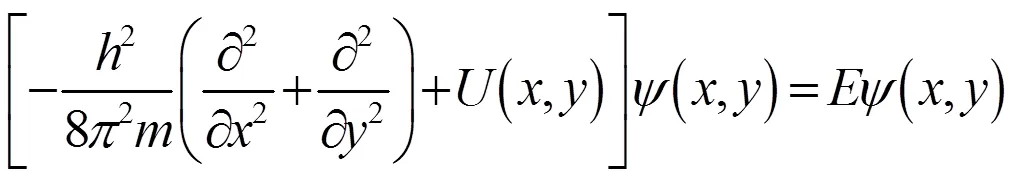
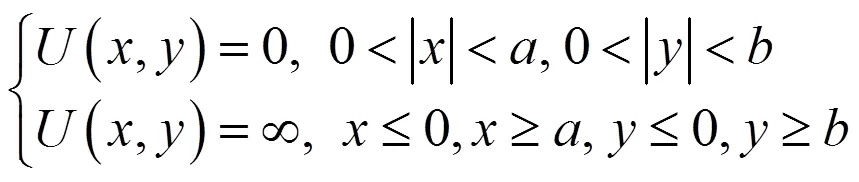
因此，二维势箱中，粒子在箱内的运动满足薛定谔方程，其表述为

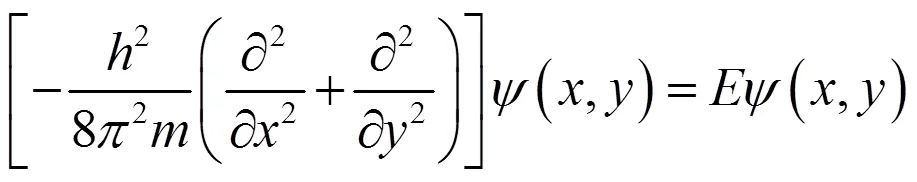
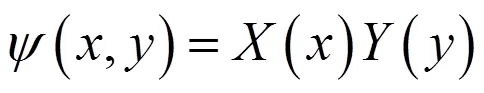
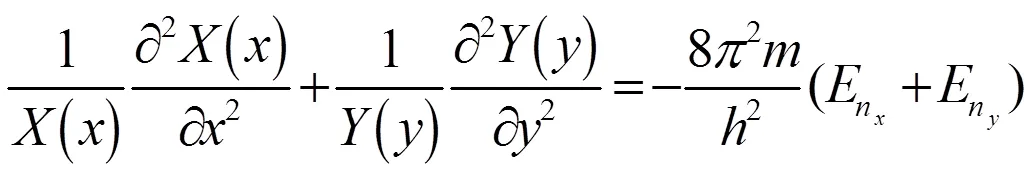
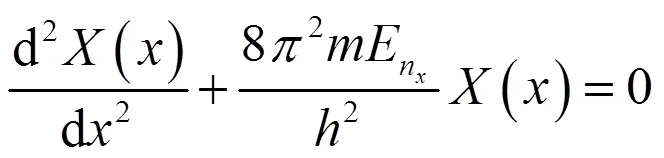
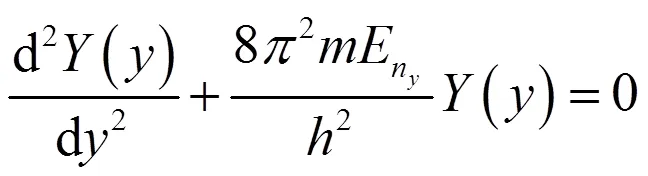
结合边界条件，利用一维势箱函数的解法，得到（5）式、（6）式的解分别为

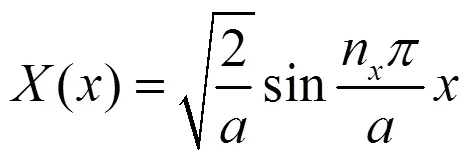
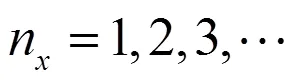
所以，二维势箱函数的波函数为

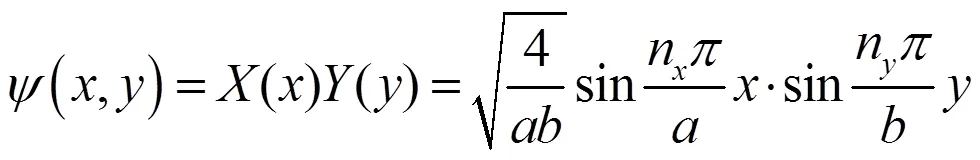
同时得到其对应的能级能量分别为

所以，二维势箱函数的总能级能量为

式中，是二维势箱长度，n，n表示势箱中粒子运动的量子数。波函数及其能级能量需要两个量子数n，n来同时描述，但不同的量子数状态可能具有不同的能量数值。

根据波函数的归一性，利用波函数几率密度的定义[14-15]，得到二维势箱函数中的粒子满足：

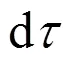
2 二维势箱函数的仿真结果与讨论

利用分离变量法推导出了二维势箱函数的波函数公式（7），为了计算的方便，取==2，即二维正方势箱函数模型。运用MATLAB软件得到了16种情况下二维势箱函数的波函数及其等值线图，如图1所示。另外，结合图1，利用波函数的理论公式和几率密度公式，还得到二维势箱函数的几率密度图及其伪真图，如图2所示。

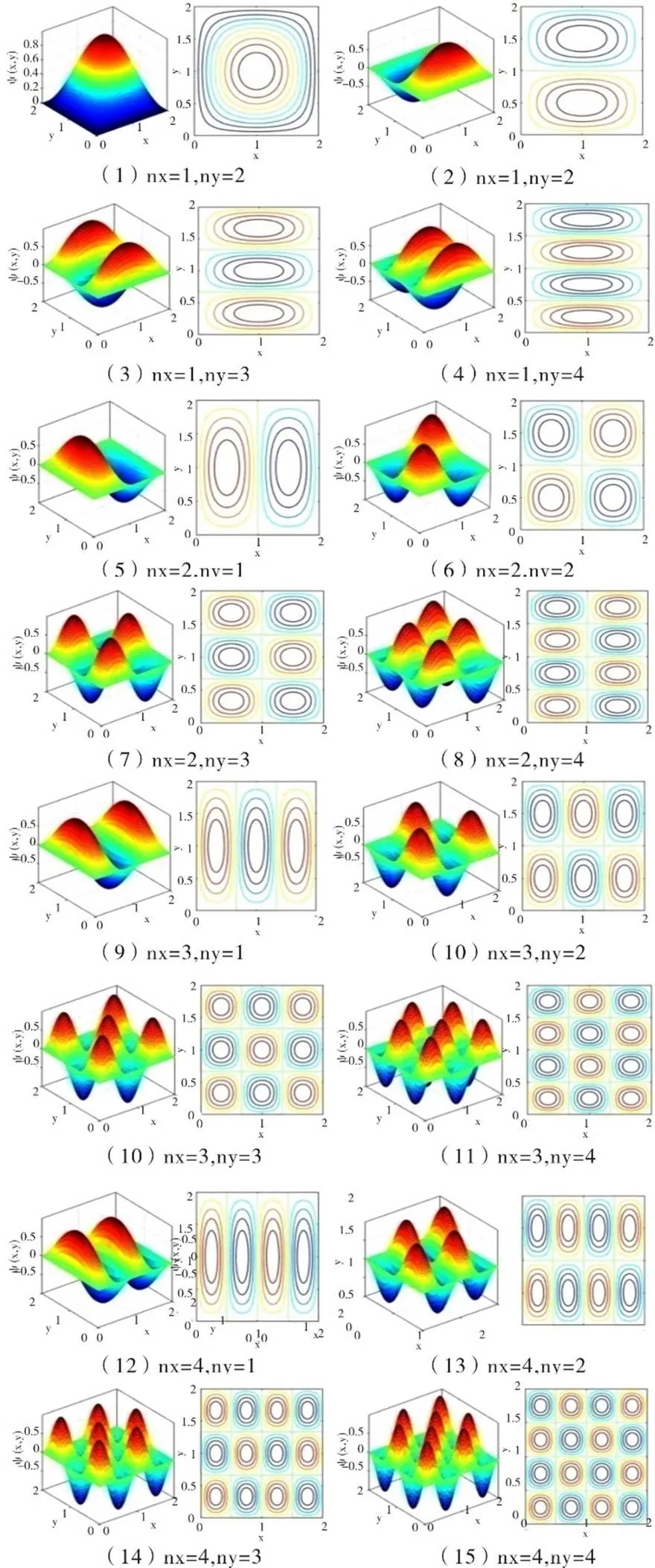
图1 不同的nx, ny对应的二维势箱函数的波函数及其等值线分布

图2 不同的nx, ny值对应的波函数几率密度及其伪真图

通过可视化的仿真图，可以得到：对于二维正方势箱函数模型，箱内微观粒子的能级简并度为n+n-1，峰值个数为n•n，且波函数与=0平面的交线数也为n•n，而且二维势箱函数的几率密度分布的极大值个数也为n•n。理论推导结果和图示结果与前人结果[5,7,10-11]完全吻合。在轴与轴组成的二维平面内，波函数图形和几率密度图形具有稳定的对称性，且成轴对称和中心对称。

3 结论

势箱函数作为量子理论的最简单、最重要模型之一，在实际生活中非常重要，是学习量子理论的基础和入门。基于数学物理思想和量子理论体系，本文运用分离变量和数值仿真相结合的方法，推导了量子理论中二维势箱函数波函数及其几率密度、能级的公式，并运用MATLAB软件仿真得到了其相关特性的可视化结果。结果表明：二维势箱函数的能级能量是不连续的、量子化的，且随着量子数的增加和势箱的长度、宽度减小而增加；二维正方势箱函数粒子的简并度为n+n-1，其峰值的个数为n•n，且波函数与=0平面的交线数也为n•n；几率密度分布的极大值个数也为n•n。另外，我们发现在轴与轴组成的二维平面内，波函数图形和几率密度图形具有稳定的对称性，且成轴对称和中心对称。本文这种可视化思路和方法解决了势箱函数教学和科学研究的难题，并为用MATLAB数值计算解决同类问题提供借鉴。这对于抽象性概念的理解具有重要意义。

[1] 周世勋. 量子力学教程[M]. 北京: 高等教育出版社, 2008.

[2] 喀兴林. 高等量子力学[M]. 北京: 高等教育出版社, 2001.

[3] 赵丹, 高策. 在真相与后真相之间——量子引力理论蕴含的时空观[J].自然辩证法通讯, 2020, 42(1):31-36.

[4] 叶世勇,费鹏. 一维势箱模型与休克尔分子轨道理论的关系[J]. 安徽师范大学学报:自然科学版, 2007(6): 672-674.

[5] 黄树芳. 在势箱中运动粒子的讨论[J]. 佛山师专学报, 1984(1): 79-81.

[6] 刘飞. 一维无限深势阱调制下的空间光孤子 [J]. 湖北师范学院学报:自然科学版,2009, 29(4): 75-78.

[7] 陈兰,孙宏伟,赖城明. 势箱中粒子的波函数与边界条件[J]. 大学化学, 2017, 32(5): 77-80.

[8] 郑兴荣. 基于第一性原理的固氦零点振动能的量子理论计算[J]. 原子与分子物理学报,2016, 33(6):1100-1106.

[9] 郑兴荣. 基于第一性原理的固氖零点振动能的量子理论计算[J]. 宁夏大学学报:自然科学版, 2016, 37(4): 429-433.

[10] 马生元. 势箱中电子运动图像的绘制[J]. 青海大学学报:自然科学版, 2002(2): 51-56.

[11] 吴其俊,龙卓,石顺超,等. 基于LabVIEW无限深势箱中粒子能级与波函数可视化程序设计[J]. 化学教育, 2015, 36(14): 67-69.

[12] 胡茂林,李新华,方国勇. 用几种不同的方法计算一维势箱中粒子的能量[J]. 中国科教创新导刊, 2008(30): 76.

[13] 刘家福,张昌芳,曹则贤. 一维无限深势阱中粒子的位置-动量不确定关系: 基于计算的讨论 [J]. 物理, 2010, 39(7): 491-494.

[14] 张树林. 基于MATLAB的能级、波函数及几率密度图形的绘制[J]. 大学物理实验, 2008(3): 102-105.

[15] 孙康瑶,赵亚男,姜其畅,等. 无限深势阱中全同粒子本征问题的数值模拟[J].运城学院学报,2017,35(3): 31-35.

[16] 郑兴荣,杨伟,张馨丹,等. 基于MATLAB对球谐函数及其原子轨道的可视化研究[J]. 四川大学学报:自然科学报, 2020,57(5): 968-974.

[17] 唐歡,郑兴荣. n维线性谐振子特性的MATLAB数值仿真[J]. 青海大学学报, 2020, 38(6): 72-79.

[18] 梁昆森. 数学物理方法[M].4版. 北京: 高等教育出版社, 2010.

[19] 张志涌. MATLAB教程[M]. 北京: 北京航空航天大学出版社, 2014.

VISUALIZATION RESEARCH OF TWO-DIMENSIONAL POTENTIAL BOX FUNCTIONS

XIE Kai-qiang, LIU Kai, WU Kun, WANG Mao-long, LI Yu-jie,*ZHENG Xing-rong

(College of Electrical Engineering, Longdong University, Qingyang, Gansu 745000, China)

Using the separated variable method and numerical simulation, the theoretical and visual results of the wave function and related properties of two-dimensional potential box function in quantum theory are obtained. The results show that the energy of particles is quantized in two-dimensional potential box. The energy increases with the quantum number, while decreases with the potential box length and width. For the square potential box function in two dimensions, the degeneracy of wave function isn+n-1, and the number of peaks isn•, and the intersection number of wave function and a plane of=0 isn•n. The number of maximum of the probability density distribution also isn•n, too. The results of the derivation and visualization in this paper are completely consistent with the theoretical results. The visualization results solve the difficult problems in teaching and scientific research of potential box function, and provide reference for solving similar problems with the numerical calculation MATLAB software. It is very significant for abstract concept to understand.

two-dimensional potential box function; separated variable method; numerical simulation; wave function; probability density; energy

A

10.3669/j.issn.1674-8085.2021.03.003

1674-8085（2021）03-0012-04

2020-12-11；

2021-02-06

国家自然科学基金项目（11565018）；甘肃省青年科技基金项目（20JR10RA135）；甘肃省教育厅高等学校创新能力项目（2019A-112）

谢凯强(1998-)，男，甘肃天水人，陇东学院电气工程学院物理系电气工程及其自动化信息专业2018级本科生（E-mail: xkq0814edu@163.com）；

刘 锴(2001-)，女，甘肃天水人，陇东学院电气工程学院物理系物理学专业2019级本科生（E-mail:2229678351@qq.com）；

吴 坤(2000-)，女，甘肃敦煌人，陇东学院电气工程学院物理系物理学专业2018级本科生（E-mail: 925799196@qq.com）；

王茂隆(1999-)，男，山西忻州人，陇东学院电气工程学院物理系电气工程及其自动化信息专业2018级本科生（E-mail: 1764483843@qq.com）；

李玉洁(2001-)，女，甘肃庆阳人，陇东学院电气工程学院物理系物理专业2019级本科生（E-mail: 2328686922@qq.com）；

*郑兴荣(1986-)，男，甘肃天水人，副教授，硕士生导师，主要从事凝聚态理论物理与材料计算、仿真的研究（E-mail:zhengxingrong2006@163.com）.