绝缘体上硅场效应晶体管热导率尺度效应模型
2021-09-10赖俊桦邢乾苏亚丽张国和
赖俊桦,邢乾,苏亚丽,张国和
(1.西安交通大学电信学部微电子学院,710049,西安;2.西安市微纳电子与系统集成重点实验室,710049,西安;3.西安石油大学机械工程学院,710065,西安)
28 nm及以下工艺节点全耗尽绝缘体上硅(FD SOI)金属氧化物半导体场效应晶体管(MOSFET)顶层硅薄膜厚度将减小至10 nm及以下尺度范围[1-4],器件特征尺寸远小于材料中传递热量的声子平均自由程,SOI器件的热生成机制与热扩散机理将变得极为复杂[5-10],自热效应对器件性能的影响变得更加显著[11-14]。目前对硅纳米薄膜热传输机理的研究尚不完善,进一步加深对硅纳米薄膜热导率尺度效应的理论研究显得尤为迫切。
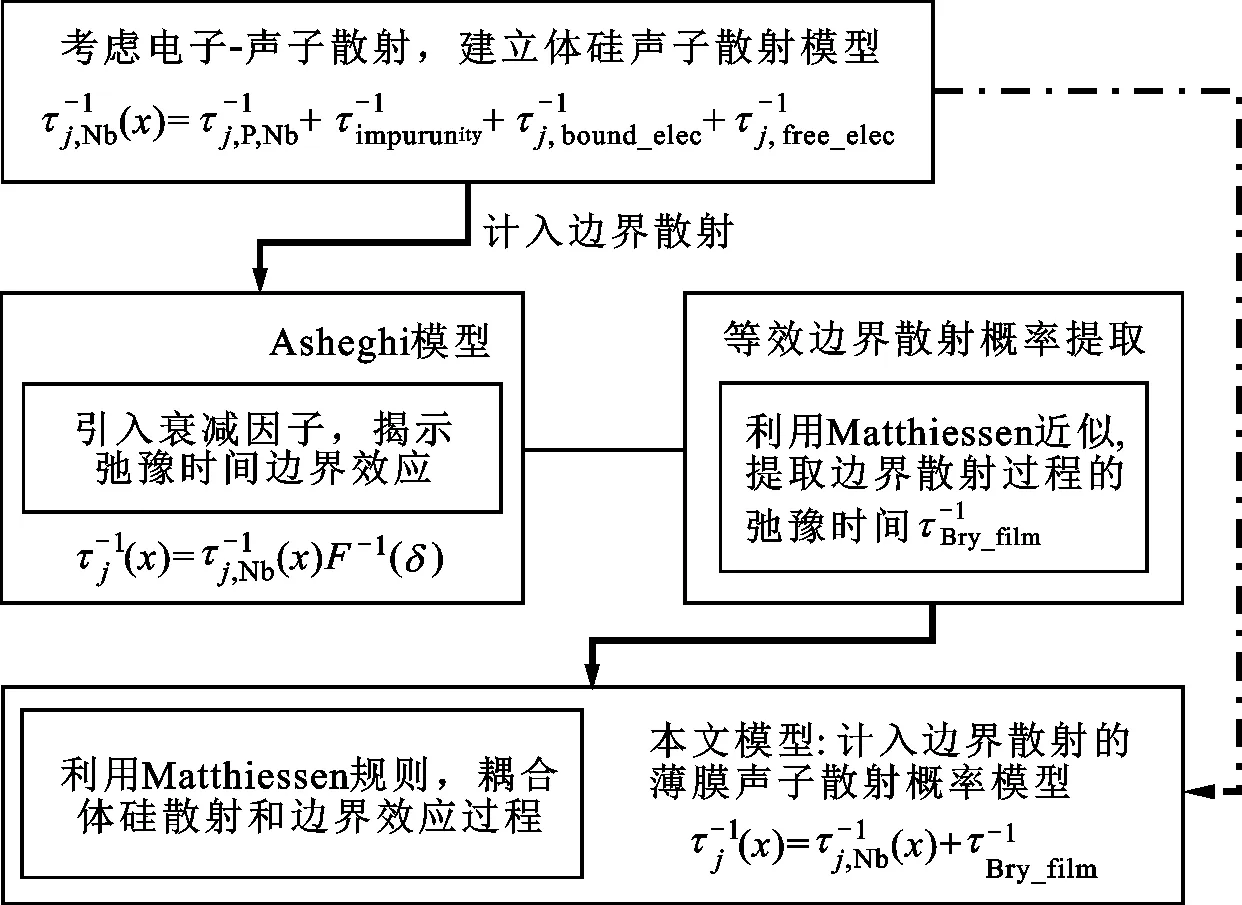
作为揭示纳米半导体器件热稳定性的关键基础,处于弹道输运状态下的纳米材料或结构的微尺度与纳尺度热传输过程被国内外研究者从数值模拟[15-18]、理论解析模型[19-22]与实验测试[23-25]等方面进行了广泛的研究。在各类热导率预测模型研究工作中取得较为成功的主要有Holland[21]和Asheghi[22]等团队。Holland硅材料热导率模型从声子散射机制的角度出发重新定义并完善了传统经验热导率模型。Asheghi则在Holland模型的基础上引入声子散射的尺度效应为微尺度硅薄膜提出依赖于材料尺寸的热导率模型,能够有效地揭示半导体器件尺寸等比缩小带来的非傅里叶热传导转变。Asheghi模型中用于衡量尺度效应的衰减因子解析形式复杂,物理意义不明显,难以用于直观、有效的预估尺度效应对热传输过程的抑制作用,不利于模型集成于TCAD数值仿真软件以实现器件热电特性的高精度数值预测,一定程度上将限制硅纳米薄膜热导率模型的广泛运用。
本文基于Holland理论模型与Asheghi的相关工作,考虑束缚态与自由态电子对声子散射的影响,简化衰减因子,获取声子边界散射等效平均自由程,为先进工艺节点FD SOI MOSFET建立起一种改进的适用于TCAD数值模拟仿真、具有简洁解析形式的硅薄膜热导率尺度效应模型,通过实验测试数据及初始模型验证了衰减因子等效简化对热导率模型的正确性。
1 热导率尺度效应模型
Holland模型是目前国际上运用最为广泛的热导率模型,能够有效地揭示声子群速度、热容与声子散射过程对材料或结构热导率的影响机制,成功地克服了传统经验模型的不足之处,其热导率表达式如下[21]
(1)
式中:j为L,T,TU,分别表示高频纵向声子模态、低频横向声子模态和高频横向声子模态;υ为声子运动速度;CV为硅材料的单位体积热容;τ为声子散射弛豫时间;Θj为德拜温度;T为硅材料温度;x为无量纲积分参数,可表示为
(2)
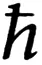
(3)
式中:δ为薄膜厚度与硅材料内声子平均自由程之比,δ=Hfilm/ιph_bulk;p为声子在边界时镜面散射的概率;F(δ,p)为考虑尺度效应的声子弛豫时间的衰减因子[22],其表达式如下
(4)
式中t为积分因子。
镜面散射概率为
(5)
式中:υs为声子平均群速度;η为硅薄膜界面粗糙度。Asheghi等在硅薄膜厚度引起的热导率衰退效应建模中用到的衰减因子F(δ,p)具有较为复杂的积分形式,很难得到考虑边界效应后声子在硅薄膜中平均自由程的变化规律。另一方面,该积分函数更加适合数值计算,不利于直观地预估硅纳米薄膜热导率的尺度效应。
为了将上述衰减因子转化为微尺度与纳尺度热传输过程中有物理意义的参数,进一步改进热导率模型,分别考虑三声子模态对热导率的贡献,将Holland模型划分为与之对应的3部分[21]
λfilm=λL+λT+λTU
(6)
式中:λL、λT和λTU分别为高频纵向声子模态、低频横向声子模态和高频横向声子模态的热导率。单位体积硅热容为
(7)
三声子模态热导率可分别表示为
λT=
(8)
λTU=
(9)
λL=
(10)
平均声子速度与各模态声子速度之间的关系为
(11)
硅薄膜内存在如图1所示的多种声子散射机制,主要有声子-界面镜面散射、声子-缺陷散射、声子-杂质散射、声子-界面扩散散射、声子-声子散射以及声子-电子散射等。因此,要建立起计入尺度效应的硅薄膜热导率模型则需要量化边界效应与尺度效应对声子散射弛豫时间的影响,结合硅材料内声子散射弛豫时间,进而得到SOI顶层硅薄膜热导率。

图1 硅薄膜内声子散射机制示意图Fig.1 Schematic diagram of phonon scattering mechanism in silicon film
1.1 硅材料热导率模型
声子-缺陷散射、声子-声子散射、声子-杂质散射和声子-电子散射是决定硅材料热导率的最重要的4种散射,其中声子-杂质散射模型能够用于描述硅材料在掺杂过程中热导率的变化规律。在没有进行掺杂的硅材料中主要存在声子-缺陷散射及声子-声子散射,这时声子散射概率为
(12)
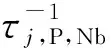
(13)
(14)
式中:Γ为硅原子与点缺陷原子之间质量差有关的参数系数;Vatom为硅原子体积。掺杂工艺是影响硅材料热导率大小的另外一个重要因素。杂质原子被引入后,主要通过与硅原子的质量差与体积差两方面抑制硅材料热导率,对声子散射概率的量化关系如下
(15)
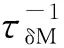
(16)
式中:AδM和AδR分别正比于掺杂原子与硅原子的质量和体积相对变化量的平方。
声子-电子散射主要包括声子和束缚态电子与自由态电子之间的散射。束缚态电子-声子散射概率为
(17)
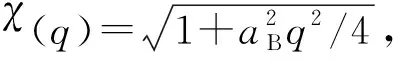
(18)
式中:me为电子质量;ED=13 meV为应变势能;ζ定义为
(19)
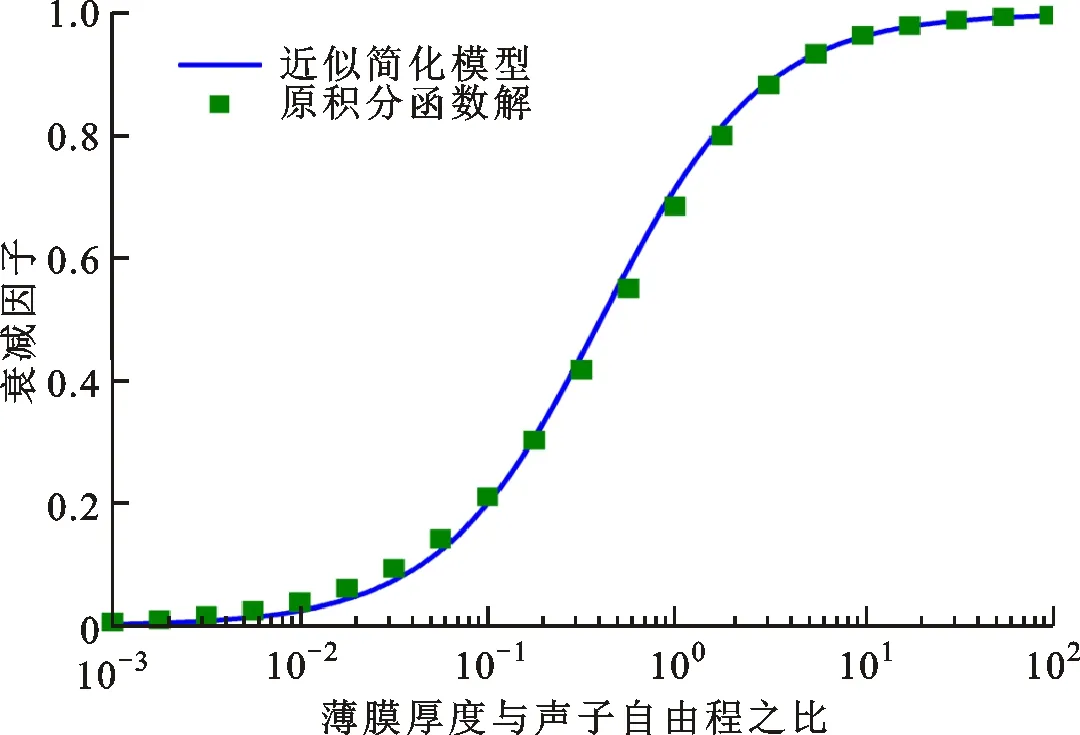
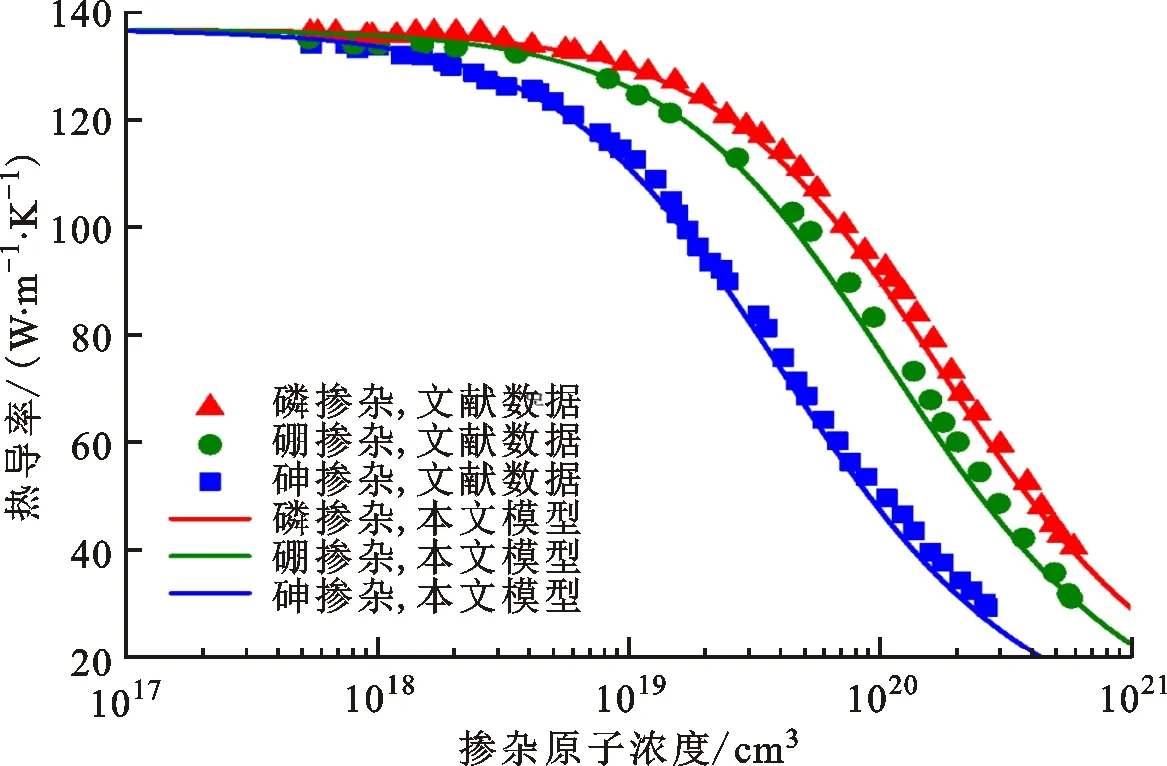
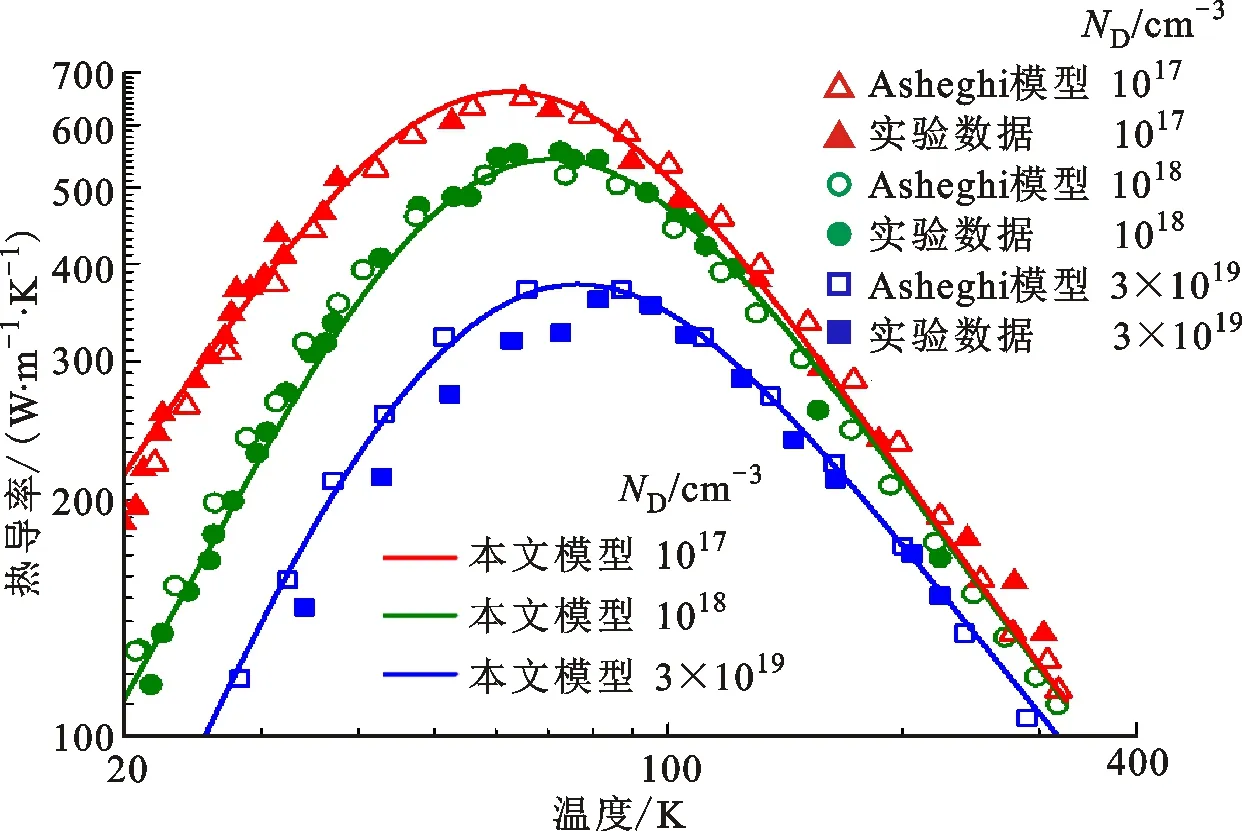
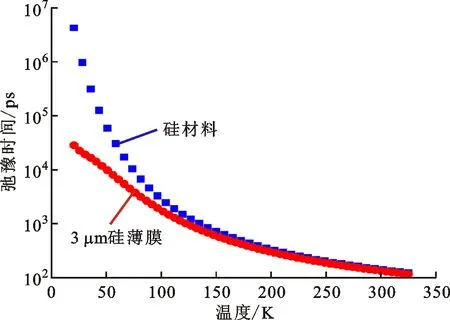
当q (20) 因此,单晶硅材料内声子-自由电子散射概率为 (21) 综上分析,考虑掺杂的硅材料声子散射概率可以推导得到 (22) 硅薄膜热导率需要在硅材料热导率的基础上进一步计入声子边界散射对声子平均自由程的影响。假设声子边界散射自由程为ιBry_film,则硅薄膜内声子总自由程可以通过Matthiessen规则得到 (23) 由此,计入尺度效应后,声子平均自由程衰退比例可以得 (24) 假设硅薄膜声子边界散射自由程是薄膜厚度的1/Φ。因为硅薄膜内声子平均自由程与硅材料的声子平均自由程之比本质上为热导率的衰减因子,那么可以将式(24)推导得到 (25) 引入Asheghi模型中衰减因子的概念,式(25)可改写成 (26) 通过式(26)与Asheghi模型衰减因子进行拟合,即可求解得到衰减因子函数所对应的硅薄膜声子边界散射自由程,实现复杂衰减因子函数的简化。由硅薄膜边界散射自由程可得声子边界散射概率 (27) 边界处声子散射类型与材料或者结构界面的粗糙度具有很强的关联性。当界面比较光滑时,界面处声子散射大概率为镜面散射,对薄膜平面内热传输没有阻碍作用。当界面比较粗糙时,界面处声子为漫反射,声子散射之后的方向存在随机性,对平面内热传输过程有重要的抑制作用。考虑镜面反射概率后,声子界面散射概率模型可以修正如下 (28) 综上分析,可以得到硅薄膜中总的声子散射概率 (29) 主要包含硅材料声子散射概率和由边界散射引起的散射概率。因此,将式(29)代入三声子模态热导率式(8)(9)和(10)中即可得到依赖于温度、掺杂原子浓度及原子种类、厚度和界面粗糙度的硅薄膜热导率模型。 图2所示为衰减因子函数简化与本文所改进的硅薄膜热导率模型建立过程。针对边界散射引起的硅薄膜热导率微尺度效应,Asheghi模型将边界效应考虑为对材料声子散射过程的抑制作用,直接为硅材料声子散射弛豫时间引入衰减因子。本文将声子边界散射过程视为一个单独过程,对Asheghi模型中具有积分形式的衰减因子进行简化,提取出等效边界散射概率,结合考虑电子-声子散射过程的硅材料声子散射模型,建立起基于Matthiessen规则的薄膜热导率模型。 图2 衰减因子函数简化与薄膜热导率模型建模过程Fig.2 Simplification of attenuation factor function and modeling of thermal conductivity of silicon thin film 为了简化Asheghi硅薄膜热导率模型中衰减因子并凸显其物理意义,求解出其等效声子边界散射自由程,本文将由Matthiessen规则得到的平均自由程衰减因子式(26)与积分形式的衰减因子式(4)进行拟合。如图3所示,当Φ等于0.4时,本文提出的近似简化模型能够与Asheghi模型[22]中原积分函数实现较好的拟合。这意味着,Asheghi模型中原积分函数的等效声子边界散射平均自由程为2.5Hfilm,将该结果导入到式(28)即可得到本文所建立的硅薄膜热导率模型。硅纳米薄膜边界将声子散射平均自由程限制于狭小空间内,薄膜厚度越小,边界散射自由程越短,严重影响硅薄膜热导率数值。 图3 积分形式的衰减因子函数及其近似简化模型对比Fig.3 Comparison of attenuation factor function in integral form and it’s approximately simplified model 当薄膜厚度与声子自由程之比越小,近似简化模型与原积分函数解间的误差将会增加,导致在对该类型硅结构热导率预测过程中将会产生较大的相对误差。例如,在无掺杂的硅材料中室温下声子平均自由程为254 nm,当薄膜厚度小于25.4 nm,即低于0.1倍的声子平均自由程时,近似简化模型与原积分函数之间将存在较大误差。当薄膜厚度为3 μm时,厚度与声子自由程之比大于10,衰减因子函数与近似解间的相对误差小于0.14%。 利用卡耐基·梅隆大学的Liu等工作中依赖于掺杂的热导率模型数据[27]对本文所提出模型进行了验证。由于原子种类不同所导致的原子质量与原子体积的不同,磷掺杂、硼掺杂与砷掺杂工艺下热导率与掺杂原子浓度的依赖关系也不同,对应的AδM与AδR分别为2.66×10-66n与8.4×10-65n,7.14×10-65n与6.29×10-65n,3.4×10-65n与3.39×10-64n。图4所示为在300 K温度下磷、硼与砷掺杂原子浓度对硅材料热导率的影响,本文所提出模型与Liu等模型能够实现很好吻合。当掺杂原子浓度低于1017/cm-3时,硅材料的热导率基本保持不变,当高于1017/cm-3时,随着掺杂原子浓度的增加,热导率急剧降低,当浓度处于1021/cm-3时,热导率仅为在无掺杂情况下的硅材料热导率的1/7左右,对热导率的抑制作用很明显。由于硼原子、砷原子与硅原子之间的相对质量差比磷原子与硅原子之间的相对质量差大很多,因此,硼掺杂与砷掺杂的AδM比磷掺杂的AδM高将近一个数量级。这也就是导致在同一掺杂原子浓度下,砷掺杂与硼掺杂的硅材料热导率比磷掺杂的热导率低的原因。砷的相对体积差相比硼的更大,导致砷掺杂对热导率的限制作用更加明显。这也说明,可以通过利用不同原子种类及原子浓度掺杂工艺的手段对材料热导率进行宏观调控,满足热电方面的实际运用需求。 图4 掺杂原子浓度对硅材料热导率的影响Fig.4 Relationship of silicon material thermal conductivity with doping concentration and type 图5为SOI器件3 μm厚顶层硅薄膜热导率随温度及磷掺杂原子浓度的变化关系,本文所建立模型能够与Asheghi模型及实验测试数据[22]较好的吻合。由于声子边界散射导致的尺度效应的存在,掺杂原子浓度为1017/cm-3的3 μm厚的硅薄膜热导率由硅材料的137 W·m-1·K-1衰减到100 W·m-1·K-1左右。随着温度的上升,SOI顶层硅热导率先增加后减小。掺杂原子浓度越高,热导率越低,热导率峰值出现的温度往高温区域移动。由式(7)计算的硅材料体积热容曲线如图6所示,可见在低温阶段,热容随着温度急剧上升,高温区域趋于缓和,最后保持不变。由热导率的经验传统公式可以求得硅薄膜内声子弛豫时间为 图5 不同浓度磷掺杂下3 μm厚SOI顶层硅薄膜热导率随温度变化关系Fig.5 Temperature dependence of thermal conductivity of 3 μm-thick SOI top silicon doped with film different phosphorus concentrations 图6 硅材料体积热容随温度变化关系Fig.6 Temperature dependence of volumetric heat capacity in silicon material (30) 根据图6中的热容关系分别求解得到硅材料及3 μm厚的硅薄膜内声子散射弛豫时间,如图7所示。随着温度不断上升,声子散射过程加剧,导致声子弛豫时间不断降低。在3 μm硅薄膜中受声子界面散射的影响,弛豫时间在50 K温度下由6×104ps降低至104ps。室温下弛豫时间由141 ps降低至133 ps。可见,微尺度与纳尺度硅薄膜由于界面散射的存在,声子散射是一个皮秒量级的高速运动过程,有限空间内热传输是一个具有极高时间与空间分辨的过程。声子边界散射的强弱决定了薄膜内声子超快热传输过程的特性。本文所提出的全耗尽SOI MOSFET硅薄膜热导尺度效应模型能够量化声子边界散射过程对热导率的影响,获得边界散射平均自由程与薄膜厚度之间的关系。因此,在本文所简化的热导率模型的基础上,结合声子群速度,即可实现对具有任意厚度的微尺度与纳尺度硅薄膜内声子热传输瞬态时间及其热传输特性的预估。高温时,由于热容及热导率趋于一致,声子散射过程由温度引起的声子-声子散射支配,声子弛豫时间趋于一致。因此,由于热容与散射弛豫时间的影响,硅薄膜低温时热导率主要是受热容的支配,随着温度上升而增加。高温区域时,声子散射过程占据主导地位,硅薄膜热导率随温度的上升而降低。图8为SOI器件3 μm厚顶层硅薄膜热导率随温度及硼掺杂原子浓度的关系,与图5中磷掺杂硅薄膜热导率变化规律一致。当掺杂原子浓度一致且在1018/cm-3时,磷掺杂硅薄膜热导率在73 K时取得峰值,最大值约为563 W·m-1·K-1;而硼掺杂硅薄膜热导率在74 K时取得峰值,最大值约为451 W·m-1·K-1。 图7 硅材料及硅薄膜声子弛豫时间随温度变化关系Fig.7 Temperature dependence of phonon relaxation time in silicon material and film 图8 不同原子浓度硼掺杂下3 μm厚SOI顶层硅薄膜热导率随温度变化关系Fig.8 Temperature dependence of thermal conductivity of 3 μm-thick SOI top silicon film doped with different boron concentrations 表1针对低温区域(小于74 K)与高温区域(大于74 K)给出了磷掺杂下热导率模型与实测数据之间的平均相对误差。可以看出模型与实测数据之间存在一定的误差,低温区域该误差将进一步增大。导致该误差产生的因素主要有两方面,首先,微尺度与纳尺度材料热特性表征存在一定的不确定度[21],这将导致模型与实测数据之间存在误差。其次,微尺度下声子边界散射在声子热传输过程中占主导地位,导致热传输界面效应明显,例如硅/二氧化硅界面粗糙度,该参数不仅与晶圆生长工艺紧密相连,同时还将受SOI MOSFET后续加工工艺的影响,如掺杂剂量、掺杂原子能量等,导致具有不同掺杂原子浓度的硅薄膜的表面粗糙度将发生改变,从而在模型与实测数据之间引入一定误差。当温度低于74 K时,声子散射弛豫时间增加,声子散射平均自由程增加,粗糙度将严重影响薄膜热导率。因此,Asheghi在工作中引入了表面粗糙度用于修正低温区域的硅薄膜热导率模型。粗糙度采用的是SIMOX工艺制备的SOI硅薄膜表面粗糙度的经验值,其值介于0.2~1 nm[21]。相比于原模型,本文提出的近似衰减因子函数在低温区域时具有更小的数值,在一定程度上强化了低温区域的声子边界散射对热导率抑制的作用,导致两模型与实测数据之间的拟合度不同。 表1 磷掺杂下热导率模型与实测数据误差对比 采用等效边界散射自由程近似的方法,简化目前国际上具有复杂解析形式,用于衡量热导率尺度效应的衰减因子函数,获取硅薄膜内声子等效边界散射平均自由程,建立起全耗尽绝缘体上硅金属氧化物半导体场效应晶体管硅薄膜热导率尺度效应模型。研究结果表明,微尺度与纳尺度硅薄膜内声子散射等效平均自由程为薄膜厚度的2.5倍。通过Matthiessen规则,将声子边界散射自由程与考虑束缚态和自由态电子-声子散射的硅材料声子平均自由程进行耦合,能够有效地实现衰减因子函数的替代。由此建立的模型与初始模型及测试数据对比表明,该等效方法能够较好地简化热导率模型,凸显衰减因子物理意义。近似处理后的模型易于集成于TCAD实现先进半导体器件自热效应的数值模拟仿真。采用薄膜厚度定义的声子边界散射自由程可广泛地运用于具有不同厚度的超薄硅薄膜结构中声子超快热传输过程的弛豫时间预估。1.2 硅薄膜热导率模型
2 模型验证与分析



3 结 论
