Evaluating soil erosion by water in a small alpine catchment in Northern Italy:comparison of empirical models

Francesca Berteni• Stefano Barontini• Giovanna Grossi

Abstract To quantify water erosion rates and annual soil loss in mountainous areas,two different empirical models were used to estimate the effects of soil erosion in a small mountain basin,the Guerna Creek watershed,located in the Central Southern Alps (Northern Italy).These two models,Revised Universal Soil Loss Equation(RUSLE)and Erosion Potential Model (EPM),were implemented in a Geographical Information System,accounting for the geographical,geomorphological,and weather-climate parameters,which are fundamental to evaluating the intensity and variability of the erosive processes.Soil characterization was supported by laboratory analysis.The results (computed soil loss of 87 t/ha/year and 11.1 m3/ha/year,using RUSLE equation and EPM method,respectively,and sediment yield of 7.5 m3/ha/year using EPM method) were compared to other studies reported in the literature for different case studies with similar topographic and climatic features,as well as to those provided by the European Soil Data Centre (ESDAC).In both cases,the agreement was satisfactory,showing consistency of the adopted procedures to the parametrization of the physical processes.

Keywords Water erosion · Alpine hydrology · EPM ·RUSLE · Soil loss · Ungauged basin

1 Introduction

The evaluation of the soil erosion rates in a basin is fundamental to developing good management practices of the territory and to identify potential hydrogeological risk areas (Auddino et al.2015).Water erosion produces damage on-site and off-site.The damage on-site occurs in the same place where water erosion happens;it includes soil loss,fertility reduction,and a decline in biodiversity.The damage off-site takes place far away from where water erosion occurs;it might consist in the increase of solid transport in rivers or damages to infrastructures.In addition,the volume of eroded material might accumulate in irrigation basins or in hydroelectric reservoirs and it may cause severe related problems such as the reduction of the storage capacity.Finally,sediments may be a dominant source of pollution in water bodies,due to the transport of fertilizers and pesticides,in agricultural areas.At the same time,soil erosion prediction and assessment is still a challenge to researchers because of the general lack of accurate information needed to properly analyze the intensity of the phenomenon.Therefore,the crucial issue of soil erosion was recently addressed during World Soil Day 2019,which was held under the theme ‘‘Stop soil erosion,save our future’’.

A wide range of models have been developed for water erosion evaluation and they differ in terms of considered processes,complexity,and required information.Generally,there is no ‘‘universal’’ model for every possible occurrence.The most suitable model should be selected after considering different factors,viz the intended use,the characteristics of the watershed,and the data availability(Ranzi et al.2012).

There are three different groups of models to calculate eroded material:physically-based models,conceptual models,and empirical models.Physically-based models require detailed information and knowledge of the basin,which is often difficult to achieve.Empirical models are widely applied because of their simplicity and ease of use,especially in countries where the availability of reliable input data is scarce.These models require less information and demand lower computation efforts than the physicallybased ones (Efthimiou and Lykoudi 2016;Jebari et al.2012).RUSLE (Revised Universal Soil Loss Equation)(Renard et al.1991) and EPM (Erosion Potential Model)(Gavrilovic 1988) are two empirical models based on formulas generated by laboratory investigations and by field observations and experiments.

In particular,the RUSLE model is the most frequently applied one in order to estimate the annual soil loss on the basis of the topography,the land-use,and the rainfallrunoff erosivity (Jebari et al.2012).Since it was first presented,the RUSLE empirical model has been increasingly applied to estimate the annual loss of soil due to surface erosion processes (sheet,interrill,and rill) in several geographical areas and at different spatial scales.As an example,we mention the cases of the Rio Centonara catchment in Emilia Romagna (2.73 km2,Italy) (Mezzini et al.2015),the Venetikos River catchment in Western Macedonia (855.23 km2,Greece) (Efthimiou et al.2016),the Lo River basin at Viet Tri (38,165 km2of which 22,600 km2are in Vietnam) (Ranzi et al.2012).The European Commission’s Soil Thematic Strategy has also proposed RUSLE model to estimate soil loss in Europe for the reference year 2010 (Panagos et al.2015e).RUSLE does not consider the sedimentation processes and it tends to over-estimate soil loss.Besides,the model is not able to simulate gully erosion,mass movements,and riverbed erosion.The application of RUSLE over the alpine territory,moreover,shows huge difficulties mainly due to data availability problems.Researchers often use simplified equations in order to estimate each factor of the equation model.The simplified equations could tend to over-estimate the measured rates of erosivity and,as a consequence,a validation based on measured data could be less meaningful.These and many other uncertainties of the RUSLE model may lead to uncertainty in the estimated erosion rate.Despite these deficiencies and shortcomings,the RUSLE methodology can produce valuable information on soil erosion processes and on their spatial distribution in mountainous areas.For example,the spatial analysis allows the identification of areas characterized by high erosion rates (Bosco et al.2008).In Italy,RUSLE model and PESARA (Pan-European soil Erosion Risk Assessment) model show that soil loss exceeds the tolerance threshold (10 t/ha/year),in approximately 30% of the Country (estimates provided JRC) (ISPRA 2013).An increasing number of tourists,changes in farming or cultivation techniques,and climate change are expected to intensify soil erosion in the Alpine area.The RUSLE-based analysis of erosion values reveals that about 20%,30%,and 50% of the alpine space is affected by high,middle,and low erosion risk,respectively (Bosco et al.2008).

The EPM describes the complex soil erosion mechanism by six individual factors linked to the land use,the land slope,the resistance to erosion,the observed erosion processes,the mean annual temperature,and amount of precipitation.It can be considered a valid tool in terms of preliminary approximation of soil loss because,despite some limitations,it allows the identification of the most susceptible areas to water erosion.This method is simple,it is very easy to use and does not require too many input data.On the other hand,the major limitation of this method is that important aspects of the phenomenon,such as sediment deposition and sediment routing,are not accounted for.Indeed,the mean annual soil loss estimated per unit area corresponds to the mean annual specific erosion of a catchment,and the fraction transported to its outlet (sediment yield) is determined by a coefficient without considering routing.The catchment soil properties are described through its lithology,while characteristics like organic matter content and granulometry are discarded.In addition,the model estimates mean annual erosion,while having very low accuracy on individual intense events,transporting most of the sediment load,especially in Mediterranean catchments (Efthimiou and Lykoudi 2016).

As a consequence of the lack of data to validate the models in many mountain areas,a model intercomparison approach may be regarded as an effective tool to estimate soil erosion.This work presents a comparison of the soil erosion estimates obtained through the application of the RUSLE and the EPM methodologies for a small mountain basin,the Guerna Creek watershed,a right tributary of the Oglio river downstream Lake Iseo (Central Southern Alps,Northern Italy).The RUSLE model was selected because it has already been applied in Northern Italy,to the whole alpine space,and in the rest of Europe in previous studies(for example,Gianinetto et al.2019;Rellini et al.2019;Bosco et al.2008),even if the aim of the RUSLE methodology is to estimate water erosion in agricultural areas.The RUSLE model is one of the most used and it is the only model in which input data can be obtained in different ways(measurement,estimation,interpolation).In addition,it has a more flexible data processing system as well as an acquired experience in the application both at the local and the continental scale.For these reasons,also considering the Guerna catchment,the RUSLE methodology was useful to evaluate water erosion in order to compare its results with EPM’s results.The EPM method was also selected because it accounts for a more complete description of the meteorological forcing since both precipitation and air temperature are included in the equation.Moreover,the EPM method is more suitable for the study area because it offers different values of coefficients connected to erosion processes (for example landslides,rill,and gully erosion)which are present in the Guerna catchment.One of the main aspects of the case is that the basin,like many other small ones in the Alps,is not gauged and it is prone to hydrogeological risk due to soil erosion.Therefore,it is important to assess strategies of comparison of different methods to estimate the annual soil loss.In addition,quantitative comparison between these two common methodologies is quite rare and this study aims at contributing with a case to the literature based on this topic.Interest in the Guerna catchment arises from (1) its geographical location,(2) the need to evaluate sediment transport and yield,expressed by the managing body of Lake Iseo and the Oglio river,and (3) the need to reduce the hydrogeological risk(Berteni and Grossi 2020).The regional local authority,Regione Lombardia,co-funded the initial phase of this research activity focusing on the analysis of the sediment yield in small mountain basins (Azioni per la montagna 2009).The project was also co-funded by Consorzio dell’Oglio.The Guerna creek was affected in the past by flooding and erosion events which stressed the hydraulic vulnerability of the study area.Therefore,this watershed is exposed to hydrogeological risk because of insufficient cleaning of the watercourse,abandonment of the territory,and of terraced-based traditional agricultural practices on the slopes (Berteni and Grossi 2020).The models were implemented in a Geographical Information System (GIS).Geographical,geomorphological and soil information were collected together with available data on meteorological forcing (precipitation and temperature data) for years between 2008 and 2011.The results obtained were compared with other case studies and with the results provided by the European Soil Data Centre (ESDAC).

The approach of comparing the application results with data coming from other cases,in the case of lack of measured data in the investigated case,is coherent with the complexity of the phenomena and deserves some interest.The high uncertainty related to the estimate of soil erosion by water is well known and even a single case study providing a comparison of the results obtained by applying established procedures may add precious value to the research.

2 Study area:the Guerna catchment

2.1 Location

The Guerna watershed is located in the Province of Bergamo (Northern Italy,Fig.1).The Guerna creek springs from Monte Foppa at 1332 m a.s.l.and it is a right tributary of the Oglio river.It flows for approximately 12.3 km before joining the Oglio river a few meters downstream of the Sarnico dam (45.66°N,9.94°E),controlling the water level in Lake Iseo (Berteni and Grossi 2020).Most of the watershed belongs to the Municipalities of Adrara S.Rocco,Adrara S.Martino,and Viadanica.The area of the basin is 30.9 km2wide,the average slope is about 27°(51%)and the average elevation is around 649 m a.s.l.The maximum difference in altitude is 1147 m:the maximum elevation is 1332 m a.s.l.and the minimum is 185 m a.s.l.

Fig.1 Guerna catchment location (Northern Italy).Yellow dots show the location of the monitoring stations used for temperature and precipitation data analysis. Source Google Maps

2.2 Topography,land use,and geomorphology

Thematic maps of the Guerna watershed (Fig.2) were produced on the basis of the data provided by the regional territorial database (http://www.geoportale.regione.lombar dia.it/).Maps show the Digital Elevation Model(DEM)for the Guerna creek catchment (5 × 5 m,Fig.2a),the derived slope map (Fig.2c) and the lithological map(limestones,marly limestones,and flint limestones constitute the soil parent material in most of the territory,Fig.2d).Close to the creek mouth gravel,sand,blocks and ferritized silt can be found (Fig.2d).Figure 2b shows the Guerna watershed land use map.It displays that most of the soil is covered by woods,reforestations,and forests.Urban areas represent a small part of the territory and they are concentrated along the Guerna creek.Fig.2e shows the study area hydrogeological instability map.There are different sites characterized by landslides,alluvial cones,debris or terrigenous cover,rill erosion,and gully erosion.

Fig.2 Thematic maps of the Guerna catchment: a digital elevation model (DEM), b land use map, c slope map, d lithological map,e hydrogeological instability map

2.3 Precipitation and temperature

Figure 3 shows the monthly averages of the precipitation at Sarnico meteorological station,197 m a.s.l.,from 2008 to 2011 provided by Consorzio dell’Oglio (http://www.oglio consorzio.it) and of the temperature (Sarnico and Ranzanico meteorological station,512 m a.s.l.,data from 2008 to 2011 provided by the regional agency for environmental protection ARPA Lombardia,(http://www.arpalombardia.it/Pages/ARPA_Home_Page.aspx).Even in the relatively short considered time window,the monthly averages recall the characteristic pattern of wet areas of the Southern Alpine range,with no dry season,two main rainfall peaks in late spring and in autumn(as in the Alpine sublitoranean climate,Bandini 1931),and a secondary peak during late summer,characteristic of the Alpine piedmont areas.The estimated average annual precipitation is 1250.55 mm/year.See Barontini et al.2009,for a more detailed report on the local climatology.

Snow melting was not considered because its effect is negligible in the considered area,as the elevation ranges between 185 and 1332 m a.s.l.Then,in the Guerna catchment,only rainfall energy leads to soil erosion.

3 Materials and methods

3.1 RUSLE modeling of the sediment erosion

The RUSLE model (Renard et al.1991) is an erosion prediction and conservation planning tool based in large part on the USLE (Universal Soil Loss Equation) (Wischmeier and Smith 1961) but including major improvements and updates.The USLE is an erosion model designed to predict the long-term average soil losses in runoff from field areas in a specific cropping and management system.A revision of this model transformed it into the RUSLE,represented by the following equation:

whereAis the computed soil loss (t/ha/year),Ris the rainfall-runoff erosivity factor (MJ · mm/ha/h/year),Kis the soil erodibility factor (t · ha · h/ha/MJ/mm),LS(–) is the topographic factor combining slope lengthLand slope steepnessS,C(–) is the cover-management factor andP(-) is the supporting practices factor.

3.2 R factor

The rainfall-runoff erosivity factor(R factor)is considered as the most important in composing Eq.(1) (Jebari et al.2012).Also,Wang et al.(2014) demonstrated,through experiments using a rainfall simulator,the need for considering the rainfall kinetic energy in developing soil erosion models.In this study,theR factor,which was considered constant over the Guerna watershed,was calculated using semi-hourly rainfall records at Sarnico from the year 2008 to 2011,considering Erosivity Index (EI)parameter (Wischmeier and Smith 1978) and the updating methods suggested by Brown and Foster(1987)in order to estimate,for each ‘‘elementary rain’’,the corresponding specific(per unit area)and unitary(per unit of rain amount)energy.

Different rainfall events were taken into account,which were separated by dry periods lasting 6 h or more.Every rainstorm was considered an erosive event.For each erosive event,the erosivity index,Re(MJ·mm/h/ha),equals the product between the specific total storm energy,E(MJ/ha),and the maximum amount of 30-min rainfall intensity,I30(mm/h):

where,according to Wischmeier and Smith (1978),63.5 mm/h represents the upper limit ofI30and the specific total storm energy(E)is the following(Bagarello and Ferro 2006):

The specific total storm energyEis evaluated through a time discretization of storm events.In fact,each erosive rain event can be divided inton‘‘elementary rains’’ with constant intensity and each of them has a specific energy,ei(MJ/ha),that was obtained by the corresponding specific(per unit area)and unitary(per unit of rain amount)energywas calculatedusing the equation proposed by Brown and Foster (1987).

The climatic factor (Raj) is the sum ofRe，kvalues,calculated for each rain erosive eventNe，jduring the yearj(Bagarello and Ferro 2006):

The rainfall-runoff erosivity factorRis the annual averageRaj(Bagarello and Ferro 2006):

During the available 4-year time series,every rainstorm was considered as an erosive event and then several meaningful erosive events were collected.In fact,high values were obtained for the climatic factor for each year.Even if the data series is not very long,a set of meaningful erosive events was sampled,stressing the importance of this basin as a hydrogeological-risk prone area.

The importance of the rainfall-runoff factor is underlined by Jebari et al.(2012),which calculated theR factorand took into account the concept of kinetic energy and the maximum rainfall intensity,as in the case of the Guerna catchment.Moreover,Jebari et al.(2012) assumed a constant and uniformR factorin their study area;which is another element in common with this study area.

3.2.1 K factor

TheK factoris usually estimated using the normograph and formulae which are published in Wischmeier and Smith (1978).However,these equations are suitable for large areas of USA,but they are not ideally suited for European conditions.For this reason,in this study,the equation proposed by Romkens et al.(1986)and revised in Renard et al.(1997) was used:

whereDg(mm) is the weighted geometric-averaged diameter of the primary soil particles:

For each particle size class(clay,silt and sand),di(mm)is the maximum diameter,di-1(mm) is the minimum diameter andfi(kg/kg) is the corresponding mass fraction.When mass fraction data are available,the estimate of theK factorcan then be performed with higher accuracy.There are other studies concerning soil erosion in Alpine space,for example,Bosco and Oliveri (2007),which used Eqs.(6) and (7) to estimate the K factor.

Also,theK factorwas considered constant over in this study area.The particle size classes were defined according to USDA (Soil Survey Division Staff 1993),for the fine soil,and the corresponding mass fractions were measured in the Hydraulics and Hydrology Lab at the University of Brescia.Two soil samples were taken in two different points of the study area:in the Northern(Adrara S.Rocco,BG) and in the Southern part (Adrara S.Martino,BG) of the watershed.The samples were dried and washed with a sieve capable of containing material larger than 75 μm.Material smaller than 75 μm,after drying,was subjected to particle sedimentation analysis.Material larger than 75 μm,after drying,was subjected to particle sieving analysis,using sieves with slotted perforations ranging from 75 to 0.075 mm.

3.2.2 LS factor

TheLS factorrepresents the effects of topography on erosion and then it accounts for slope length and slope steepness on soil loss.This factor is the main innovation of the RUSLE model,in comparison with the original model(USLE):it considers the flow convergence and it is the result of the combination of the slope(S)and of the length(L).

The LS factor can be determined through GIS procedures using the relation of Moore and Burch(1986),but in complex hillslopes (in particular when slope morphology presents great spatial variability) this relation can be problematic (see also Engel and Mohtar 1999;Mitasova and Brown 2002).The topographic complexity of the alpine territory poses significant challenges in estimating the S factor.Therefore,as suggested by Bosco and Oliveri(2007) who used this equation for the alpine territory,in this study Moore and Burch’s equation (1986) was modified using the S factor that was evaluated by Nearing’s formula (Nearing 1997);it provides more reliable results for higher slope values (more than 50%):

where α is the slope (in degrees),Cell_sizeis the pixel dimension andFlowaccconsists of the number of cells bringing runoff water to each pixel in the grid.

In GIS applications to long mountain slopes,it is usually considered that above a flow accumulation value,corresponding to about 300 m of slope length,water starts flowing in channels,which are not considered by the RUSLE.In the study area,taking into account the pixel dimension (5 m × 5 m),the maximum value of this parameter is equal to 60 cells.Therefore,this flow accumulation value was considered the upper limit of the flow accumulation parameter,which consists of the number of cells bringing runoff water to each pixel in the grid(Pregnolato and D’Amico 2011).TheLS factormap(spatial resolution:5 m × 5 m) was created in a GIS environment on the basis of the slope map(Fig.2c)and of the flow accumulation map;therefore spatial variability of this factor was considered.

3.2.3 C factor and P factor

The cover-management factor(C factor) describes the effects of cover and land use on average annual soil loss.It represents the relation between the soil loss in the agricultural or cover conditions and the erosion that would be obtained from a standard fallow parcel (bare soil).This factor is very important in soil loss estimation because it represents conditions that can be most easily modified to reduce erosion.TheC factordepends on changes (in terms of environment cultivations,agricultural activities,residual management,and on the morphology of the trees during the year)and different soil cover typologies may have different values.For these reasons,together with the lack of detailed information and with the difficulties in processing all factors on a large scale,RUSLE guidelines are not completely clear about the estimate of theC factor.Therefore,average values reported in the scientific literature were used.

The supporting practices factor(P factor) reflects the impact of support practices on the average annual erosion rate.This factor is the soil protection factor and it primarily represents how surface conditions affect flow paths and flow hydraulics.TheP factorexpresses soil protection from erosion regarding human practices and it is usually set to 1 when these practices are not applied.In this study,Pwas considered to be smaller than 1 only in areas occupied by orchards and vineyards because they are terrace cultivations.These areas have an average slope greater than 24%,which is the upper limit suggested by Wischmeier and Smith 1978;therefore,aPvalue corresponding to the maximum value was associated with them.Table 1 showsC factorandP factorvalues for the Guerna catchment,that were associated with each category in the land use map (Fig.2b).

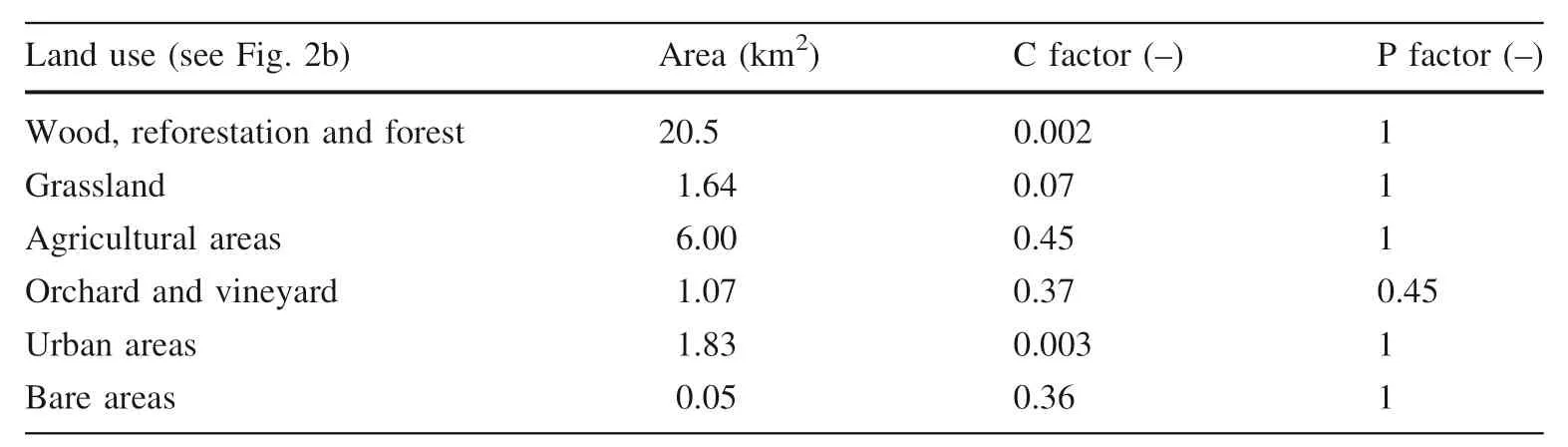
Table 1 C factor values(Angeli 2004) and P factor values (Wischmeier and Smith 1978)

The C factor map and the P factor map (spatial resolution:5 m × 5 m) were created in a GIS environment on the basis of the slope map (Fig.2c);therefore spatial variability of these factor was considered.

3.3 The EPM modelling of sediment erosion

The EPM method (Gavrilovic 1988) is an empirical semidistributed model to estimate the mean annual volumes of soil erosion and sediment yield at the basin scale.Thismodel combines,in the following simple structure,all the most statistically significant parameters controlling soil particle detachment and transport (Gavrilovic 1988):

wherewspis the average annual specific production of sediments (m3/km2/year),His the mean annual amount of precipitation (mm),Tis the temperature coefficient[Eq.(10)] andZis the coefficient of erosion [Eq.(11)]

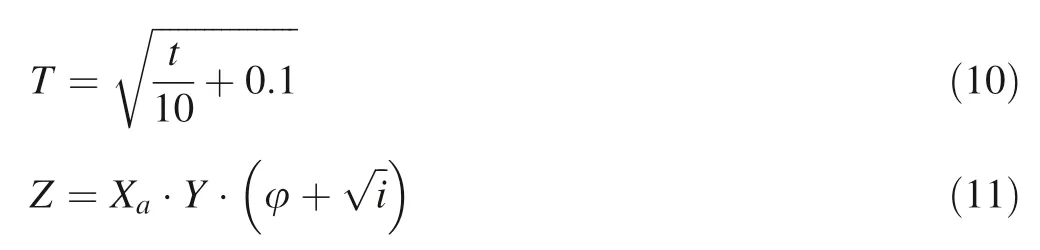
wheretrepresents the mean annual temperature(°C),Xais the land use coefficient,Yis the coefficient of soil resistance to erosion,φ is the coefficient value for the observed erosion processes andiis the average land slope (m/m).The computation of the coefficientZis described in detail in the next subchapter.

The average annual production of erosional sediments in the catchment areaWg(m3/year) is the product between surface areaA(km2) and the weighted average annual specific sediment productionwsp:

Finally,only a fraction of the total sediment volume that is produced within a catchment reaches out to its outlet.The effective sediment transported by the stream to the outlet of the watershed is the mean annual basin sediment yieldG(m3/year) and it is determined by the sediment retention coefficientRu:

whereO(km) is the perimeter of the catchment,L(km) is the length of the principal waterways andD(km) is the mean level difference in the basin,which is the difference between the mean altitude of the basin and the level of the outlet section.

3.3.1 Coefficient of erosion Z

The coefficient of erosion (Z) was calculated considering the spatial variability of each term in Eq.(11).Table 2,Table 3,and Table 4 show respectively categories used to attributeXa,Y,and φ values[used to solve Eq.(11)]in the Guerna catchment.Values were set according to Milanesi et al.(2015),referring to a mountainous area in the North of Italy.Xacoefficient was computed by associating a value to each area in the land use map(Fig.2b),Ycoefficient was obtained by associating a value to each area in the lithological map (Fig.2d) and φ coefficient was obtained by associating a value to each area in the hydrogeological instability map (Fig.2e).The coefficient of erosion(Z) map was obtained in a GIS environment.

3.3.2 Mean annual amount of precipitation H and temperature coefficient T

The mean annual amount of precipitation (H) was considered constant over the entire study area and it was calculated by aggregating daily precipitation data from the year 2008 to the year 2011,recorded at Sarnico (Fig.3).

Fig.3 Mean monthly precipitation at Sarnico and mean monthly temperature at Sarnico and Ranzanico (from 2008 to 2011)

The temperature coefficient (T) was calculated by Eq.(10),taking into account its spatial variability by means of a monthly linear trend computed on the basis of the available data in Sarnico and Ranzanico (Fig.3).The minimum and maximum estimated temperature gradients are -0.03 °C (in January) and -0.7 °C (in July) every 100 m of altitude,respectively.A monthly temperature map for each month was created and the 12 monthly temperature maps were used to build the mean annual temperature map.

4 Results and discussions

4.1 The RUSLE modelling of sediment erosion

The obtainedR factorvalue was 2336 MJ·mm/ha/h/year.

Table 5 shows the useful results of the particle analysis and theK factorfor each soil sample.

Table 2 Land use coefficient Xa (Milanesi et al.2015)

Table 3 Coefficient of soil resistance to erosion Y(Milanesi et al.2015)

Table 4 Coefficient value for the observed erosion process φ (Milanesi et al.2015)

On the basis of this analysis,theKvalue used for the study area wasK=0.038 t·ha·h/ha/MJ/mm.

Figure 4a shows theLS factormap that was created.C factorandP factormaps were also built,using values given in Table 1 in the land use map (Fig.2b).Thecomputed soil loss Amap with a spatial resolution of 5 m (Fig.4b) was calculated in a GIS environment for the Guerna watershed through Eq.1.Results are the following:

Fig.4 Guerna catchment: a LS (-) factor map and b map of computed soil loss A (t/ha/year) using RUSLE

Table 5 Results of the particle analysis and K factor

•A_mean=87 t/ha/year or 0.22 t/cell/year

•A_tot=269,140.9 t/year

4.2 Comparison with the European Soil Data Centre (ESDAC)

The mean value of each RUSLE factor shown in ESDAC(European Soil Data Centre,https://esdac.jrc.ec.europa.eu/)maps for the Guerna catchment location were compared with the values reported in the previous paragraph.ESDAC is the thematic centre for soil-related data in Europe and it is hosted by the Joint Research centre (JRC)of the European Commission.

The mean value of the rainfall erosivityR factorin the Guerna catchment and provided by ESDAC is 2290 MJ · mm/ha/h/year,considering a spatial resolution of 500 m.The period covered for the precipitation data(temporal resolution:30 min) collected to estimate theR factoris between 2002 and 2011.ESDAC calculated theR factoras the product of kinetic energy of a rainfall event(E)and its maximum 30-min intensity(I30)(Panagos et al.2015a).This value,evaluated by using the same procedure described in this study,has the same order of magnitude as that computed by us (2336 MJ · mm/ha/h/year).Figure 5a shows the map ofR factorvalue in the North of Italy provided by ESDAC.

ESDAC estimated theP factorconsidering a spatial resolution of 100 m and it assigned a value of 1 for the Guerna catchment area as a whole.This value is in accordance with the mean value adopted in this study (P factor=0.98),in which a spatial resolution of 5 m was used.At the European level,theP factorwas proposed as a product of three sub-factors:contour farming,maintenance of stone walls,and grass margins (Panagos et al.2015d).Figure 5b shows the map of the support practiceP factorfor North of Italy provided by ESDAC.

The mean value of the cover-managementC factorestimated by ESDAC in the Guerna catchment,using a spatial resolution of 100 m,is 0.028.ThisC factorvalue is almost four times lower than the mean one used in this study (C factor=0.105).The reason relates to the higher level of detail and to the different methods used for its evaluation.In fact,most of the basin (20.5 km2) is a wooded area (C factor=0.002),but theC factorassociated to agricultural area(6 km2)is 0.45;for this reason,the mean value of theC factoris higher than the value provided by ESDAC.The estimation of theC factorin the European Union considered a hybridC factorland use and management (LANDUM) model,developed for the European-scale study.It is based on a literature review,remote sensing data at high spatial resolution,and statistical data on agricultural and management practices.The LANDUM model for C factor estimation was differentiated between arable lands and all other land uses (non-arable),considering the combination of different sub-factors.Finally,a mosaic layer of theC factorfor arable lands and for nonarable lands was proposed as the annualC factorin Europe(Panagos et al.2015c).Figure 5c shows the meanC factorvalue in the North of Italy provided by ESDAC and estimated with LANDUM procedure described in Panagos et al.(2015c).

The mean value of theK factorprovided by ESDAC in the Guerna catchment is 0.027 t · ha · h/ha/MJ/mm,considering as a spatial resolution of 500 m.ThisK factorvalue is similar to the value estimated in this study (K factor=0.038 t · ha · h/ha/MJ/mm).At the European level,with the Land Use/Cover Area frame Survey(LUCAS) topsoil data (Toth et al.2013),theK factorwas calculated using an algebraic approximation of the nomograph (Wischmeier and Smith 1978).This equation includes five soil parameters (texture,organic matter,coarse fragments,structure and permeability).A regression model was applied to correlate spatial data such as latitude,longitude,remotely sensed,and terrain features in order to develop a high-resolution soil erodibility map in Europe.Therefore,theK factorvalue of each LUCAS point sample was interpolated to derive a continuous map for Europe(Panagos et al.2014).Figure 6(a) shows the map of Soil Erodibility estimated as theK factorin the North of Italy and provided by ESDAC.

Fig.5 a High-resolution map of rainfall erosivity, b support practice P-factor and c C factor map in Europe (North of Italy).Zoom on the Guerna catchment(https://esdac.jrc.ec.europa.eu/)

The mean value of the slope length and steepness factor(LS factor) estimated by ESDAC in the Guerna basin is 7.73.This value is half of the mean value calculated in this study (LS factor=14.09).The reason relates to the higher level of detail and to the different methods used for its evaluation,as reported in paragraph 3.2.2.The resolution of the DEM adopted in this study is 5 m and a surface runoff concentration in less than 300 m was assumed.The grid-cell size is very important for theS factor,since the slope decreases as the cell size increases (Molnar and Julien 1998).When DEM resolution and accuracy increase,the landscape is more accurately described,the soil erosion topographic factor is calculated precisely and erosion estimates approach actual values.Then DEM resolution has profound consequences on the spatial pattern of theLS factor.For the Italian case study,theLS factorestimated by ESDAC was calculated using GIS software tools with highresolution (25 m) DEM;the methodology applied is the Desmet and Govers(1996)algorithm and the estimation of this factor is limited to a maximum slope angle of 50%(26.6°) (Panagos et al.2015b).Figure 6b shows the slope length and steepness factor(LS factor)in the North of Italy provided by ESDAC.

It follows from this analysis in particular that the RUSLE factors estimated in paragraph 4.1 are similar to the factors proposed by ESDAC in the Guerna catchment;they have the same order of magnitude,despite the formers are always higher than the latter.Higher differences are especially visible inC factorandLS factorvalues.This result makes sense because of the DEM higher resolution adopted,of a more detailed land use map and of the availability of direct measures of grain size distribution.

4.3 The EPM modeling of sediment erosion

Figure 7a shows the obtained coefficient of erosion (Z)map,accounting for the land use coefficientXa(Table 2),the coefficient of soil resistance to erosionY(Table 3),the coefficient for the observed erosion process φ (Table 4)and the slope map (Fig.2c).Figure 7b shows the temperature coefficient (T) map which was created.The mean annual amount of precipitation (H) has a value of 1250.55 mm/year.

The map of the average annual production of erosional sedimentWg(Fig.7c)was calculated in a GIS environment for the Guerna watershed through Eq.(12),whereAis the DEM cell area (A=0.000025 km2).The mean value(Wg_mean) and the total value (Wg_tot) of sediment production for the Guerna catchment of computed soil loss are the following:

Fig.6 a High-resolution(500 m grid cell size) map of Soil Erodibility estimated as K factor and b slope length and steepness factor (LS-factor) in Europe (North of Italy).Zoom on the Guerna catchment(https://esdac.jrc.ec.europa.eu/)

Fig.7 Guerna catchment: a coefficient of erosion Z (-) map, b temperature coefficient T (-) map and c map of computed soil loss Wg (m3/year) using EPM

•Wg_mean=0.028 m3/cell/year

•Wg_tot=34,193.2 m3/year

Equations (14) and (13) were used to calculate respectively the sediment retention coefficientRuand the mean annual basin sediment yieldG:

•Ru=0.677

•Gtot=23,156.1 m3/year

•Gmean=7.5 m3/ha/year

The sediment yield value is the effective sediment transported by the stream to the outlet of the catchment.This value is useful in order to compare the estimated sediment volume for the Guerna watershed to records of sediment volumes extracted from reservoirs,which are located at the downstream section of different watersheds in Northern Italy.

4.4 Comparison between RUSLE and EPM model and other literature case studies

The soil loss computed for the Guerna catchment with the RUSLE and the EPM approaches are summarised in Table 6.By considering a particle density of 2.65 t/m3,as suggested by Efthimiou et al.(2016),soil loss computed for the Guerna watershed in the years 2008–2011 by the RUSLE equation is around three times higher than its evaluation according to the EPM method.Moreover,the adopted value of particle density,which is suitable for rocks,is typical for limestone which covers most of the study area,as shown in the lithological map (Fig.2d).

This overestimate is coherent with the results obtained for another case study(Sfalassa Fiumara,Southern Italy),with a similar topography (Auddino et al.2015;Dominici et al.2015).The Sfalassa` Fiumara catchment is located in the south western slope of Aspromonte Massif (Southern Calabria).It has an area of 24.2 km2,the altitude ranges from 0 to 1174 m a.s.l.and has an elongated shape.In the mountain area of this basin,the average annual precipitation and temperature are respectively 1550 mm/year and 13 °C.These values are similar to those recorded at Sarnico station.In this watershed,the Gavrilovic’s EPM model was applied by the use of spatially distributed input data on geology,soils,and land use in a geographic information system environment.Three evaluations of the Sfalassa` Fiumara catchment erosion were carried out by Auddino et al.(2015),changing the coefficientXa,Yand φ.In the first evaluationXaandYfactors came from the geological map of Calabriaand Corine 2000.The second evaluation was integrated by to definition of the grade weathering and RMR (Rock mass Rating) related to the values of Zemljic’s Table (1971).In the third evaluation,the basin was divided in three smaller,more homogeneous,sub-basins and the Sfalassa` Fiumara catchment showed a strong spatial variability inT,HandZ;an intersection of different dataset (Xa,Yand φ) was operated in GIS environment.Results obtained by the three evaluations are=37,699 m3/year,=45,075 m3/year,=48,062.5 m3/year (Auddino et al.2015).Moreover,it is recognized by other studies (for example Yesuph and Dagnew 2019;Renard et al.1991)that RUSLE model is prone to overestimate soil losses.

Table 6 Summary of the results of soil losses in the Guerna catchment

The RUSLE methodology was first developed to estimate water erosion in agricultural area,therefore the approach is not expected to be well suitable for erosion assessment in mountain catchments(Dominici et al.2015).In Bosco et al.(2008) study it is said that the most common soil erosion models,such as the RUSLE,are meant to be used on hilly agricultural areas where sheet and rill erosion processes prevail.Nevertheless,Bosco et al.(2008)decided to use the RUSLE model in an alpine environment because of its wide usage and usability (it is in fact the only model in which input data can be obtained in different ways;measurement,estimation,interpolation).In addition,it has a more flexible data processing system as well as it has been applied several times both at the local and the continental scale(Bosco et al.2008).For these reasons,also for the Guerna catchment,the RUSLE methodology was useful to evaluate the effect of water erosion and compare its results with EPM’s results and other case studies.

Table 7 list the results achieved by the statistical treatment of soil loss data obtained for RUSLE and EPM model,(also represented in Fig.4b and in Fig.7c).

Table 7 Results of the statistical trend of the data in the Guerna catchment,using RUSLE and EPM model

Finally,because of the lack of sediment yield observations to validate the simulation results,some proxy data were used for this purpose.The first case study is the Tartano basin (Fig.8),a 49-km2wide sub-basin of the Adda catchment located in Lombardy as well.Elevation in this catchment ranges from 950 to 2250 m a.s.l.,the mean annual rainfall value is 1376 mm/year,the average slope gradient is 55%,the climate is Alpine continental and the downstream section is placed at the Campo dam where annual data on the reservoir silting are collected.The mean annual sediment volume (from the year 1991 to the year 1998) that was taken out of the Campo dam is 38,038 m3(Brambilla et al.2011);this value,thatcorresponds to 7.8 m3/ha/year,is very similar to the sediment yield estimation (Gmean) in the Guerna catchment.The second case study is the Valgrosina reservoir (Fig.8),which is located in the alpine valley of Valtellina(Rhaetian Alps—Lombardy) in Northern Italy,approximately 1200 m a.s.l.The drainage area at the dam section is about 60 km2and it extends over a mountainous area,with no significant human activities.The annual sediment volume removed from the reservoir is 20,000 m3(3.3 m3/ha/year)and 35,000 m3(5.8 m3/ha/year),respectively in the year 2006 and in the year 2007(Espa et al.2013;Pagliari et al.2017;Castelli et al.2010);these values have the same order of magnitude as the sediment yield(Gmean)estimated in this work for the Guerna catchment.

Fig.8 Guerna catchment,Tartano basin(reservoir at the Campo dam)and Valgrosina reservoir location(Northern Italy).Source Google Maps

Table 8 summarises the comparison between simulation results of sediment yield in the Guerna catchment and sediment volumes extracted from the reservoir at the Campo dam and from Valgrosina reservoir.

Table 8 Summary of simulation results and field observations of sediment yield

5 Conclusions

Empirical models are still considered as a valuable tool to estimate water soil erosion in mountainous areas,where detailed knowledge of the soil properties is seldomavailable and a preliminary estimate of sediment production is on the other hand requested to plan best management practices.Because of the lack of data for the validation of the models,a model intercomparison may be regarded as an effective strategy.In view of increasing the literature base of model intercomparison,in this study,two empirical methodologies (RUSLE and EPM) were tested and compared by analyzing their results when applied to a small alpine catchment,the Guerna watershed,located in Northern Italy.

The average value and the total value of computed soil loss using RUSLE equation were,respectively,87 t/ha/year and 269,140.9 t/year.The values of computed soil loss and sediment yield using EPM method were 34,193.2 m3/year(corresponding to 11.1 m3/ha/year) and 23,156.1 m3/year(corresponding to 7.5 m3/ha/year) respectively;by considering a specific weight of 2.65 t/m3,the computed soil loss values were 29.3 t/ha/year and 90,612 t/year.

Results showed that soil loss computed for the Guerna watershed by the RUSLE equation was about three times higher than its evaluation according to the EPM method.On the one hand,the overestimate may be due to the fact that the RUSLE methodology was originally developed to estimate water erosion in agricultural areas and not in mountain areas.On the other hand,the EPM method accounts for a more complete description of the meteorological forcing since both precipitation and air temperature are included in the equation and might in principle be more suitable for mountainous areas.

Validation was performed by comparing the results obtained using both methodologies with others reported in the literature for other case studies with similar features.The overestimate using RUSLE equation is coherent with the results obtained for Sfalassa` Fiumara catchment,located in Southern Italy,with similar topographic and climatic features (Auddino et al.2015;Dominici et al.2015).Moreover,the estimated sediment yield value has the same order of magnitude as sediment volumes extracted from reservoirs,which are located at the downstream section of a different watershed in Lombardy (Northern Italy).

In addition,the comparison analysis showed that the RUSLE factors calculated are similar to the factors proposed by ESDAC for the area including the Guerna catchment.Despite the discrepancy in the results,the two empirical models show consistency with respect to the underlying parametrization of the physical processes and provide precious insights in the preliminary delineation of the areas most affected by water erosion.

Even with the limitations of empirical models,this study contributes to the existing literature on soil erosion,which is a very important topic today.In addition,because of the interest of Italian local authorities,these evaluations can be considered preliminary to further research activities for models’validation using sediment yield observations when they become available.

AcknowledgementThis work was supported by MC s.r.l.,by the university research project(University of Brescia)Health and Wealth 2015 ‘URBAID (Rigenerazione urbana assistita e integrata)’ and by the call H2020-SwafS-2016-17 Science with and for Society (European project:‘‘SciShops’’:Enhancing the Responsible and Sustainable Expansion of the Science Shops Ecosystem in Europe).

Compliance with ethical standards

Conflict of interestThe authors declare that they have no conflict of interest.