基于离散频谱校正的差分吸收光谱数据处理方法研究

贾桂红，张建军，郑海明

（1.河北工业大学 机械工程学院，天津 300401；2.华北电力大学 能源动力与机械工程学院，河北 保定 071003）

1 引言

差分吸收光谱法（differential optical absorption spectrum，DOAS）不需要抽取采样，可以实现在线连续监测，在环境监测领域得到了广泛的应用［1～3］。

差分吸收光谱法的关键技术在于去除测量过程中的噪声，准确获取被测气体的特征吸收光谱。傅里叶变换是在变换后的频谱中去除慢变化，达到降噪的目的。刘前林等［4］利用傅里叶变换后的频谱的幅值反求气体的浓度；Zhang X X等和周红等［5，6］利用快速傅里叶变换对SO2的差分吸收光谱进行分析；郑海明等［7］利用傅里叶变换和傅里叶逆变换对臭氧数据进行分析，但是由于时域截断而产生能量泄露，导致变换后的频谱的幅值、频率和相位存在较大误差；王宁等［8］采用Mertz乘积法对系统的相位误差进行校正；郑海明等［9］利用线性调频Z变换对傅里叶变换后的频谱进行局部细化，对FFT算法的误差进行补偿；郁敏捷等［10］在FFT变换的基础上采用经验模态分解进行降噪，取得一定的进展。

为了解决傅里叶变换光谱分析算法所带来的误差，本文采用离散频谱主瓣内谱线的重心求出峰值的坐标，对频谱进行校正后再对所测气体进行浓度反演，并进行了实验验证，提高了浓度反演精度。

2 理论分析模型

差分吸收光谱法气体浓度监测实验装置如图1所示。待测气体SO2和载气N2按比例通过质量流量控制器（MFC），达到所要求的气体浓度，进入吸收池进行混合。光源发出的原始光强I0（λ）和光谱仪接收到的光强I（λ）之间满足Beer-Lambert定律［11～13］：

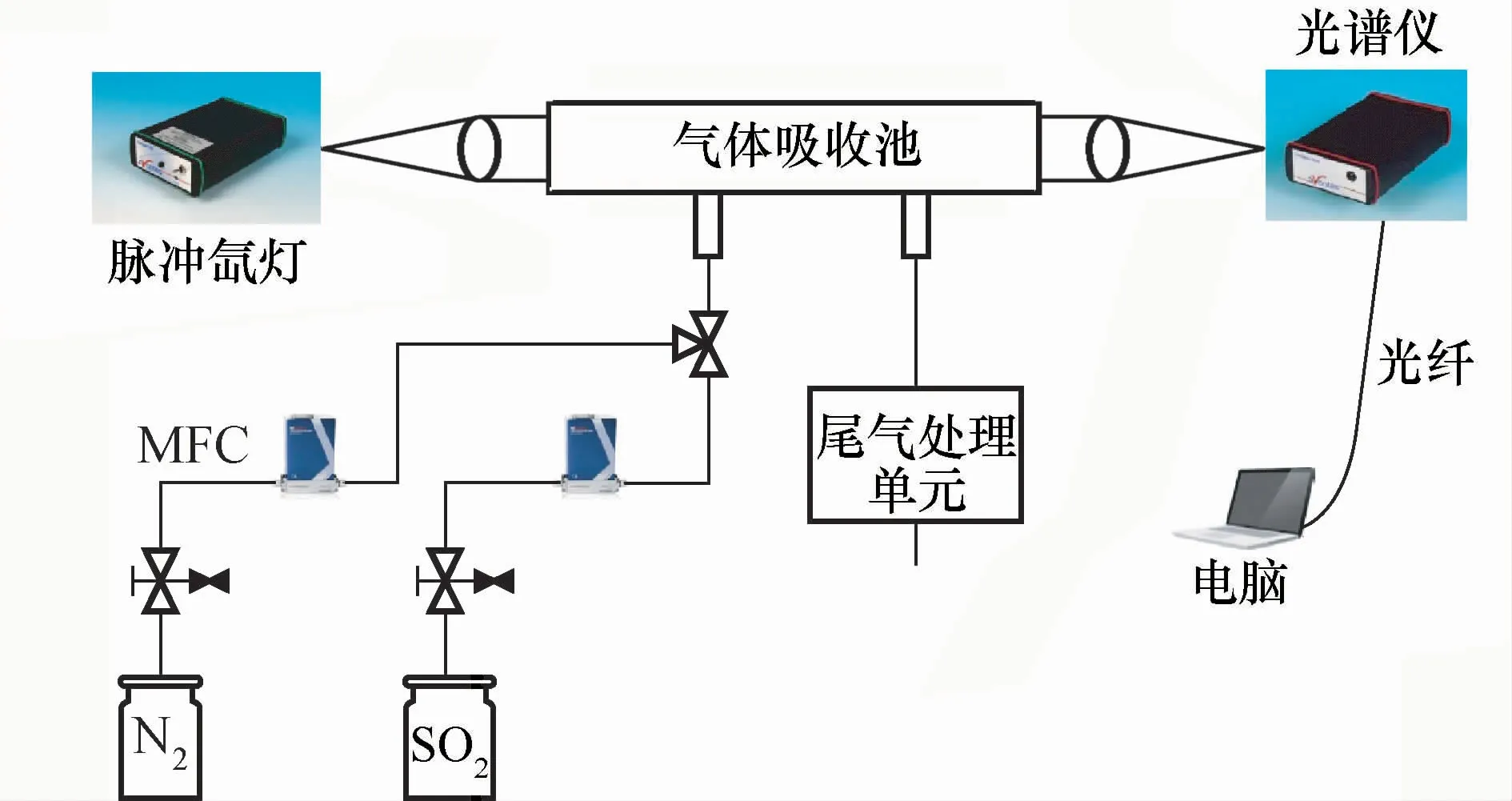
图1 实验原理图Fig.1 Schematic diagram of experimental system

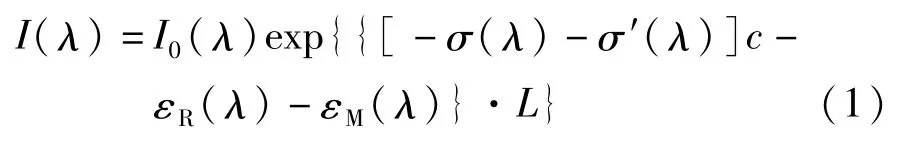
式中：λ为波长；σ′（λ）和σ（λ）分别表示随波长缓慢变化的“宽带”吸收截面和快速变化的“窄带”吸收截面；εR（λ）和εM（λ）分别表示瑞利散射和米氏散射系数；c为被测气体的浓度；L为吸收池的长度。

定义气体的光学密度（optical density）D（λ）

光学密度是一个无量纲量，衡量了气体对光强的衰减程度。对式（1）两边取对数，得到光学密度：

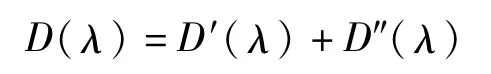
其中，

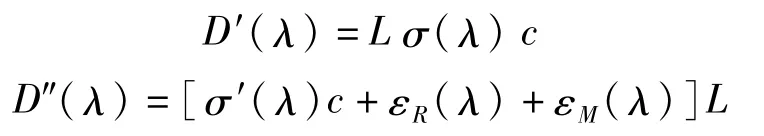
式中：D′（λ）为“快变”，由被测气体的窄带吸收特性决定，随波长快速变化；D″（λ）为“慢变”，σ′（λ）、εR（λ）和εM（λ）随波长作慢变化，可以通过多项式拟合得到；差分吸收光学密度D′（λ）＝D（λ）－D″（λ）。

根据D′（λ）可以计算出被测气体的浓度为

3 光谱数据处理方法

图2为SO2气体的光谱图和频谱图。

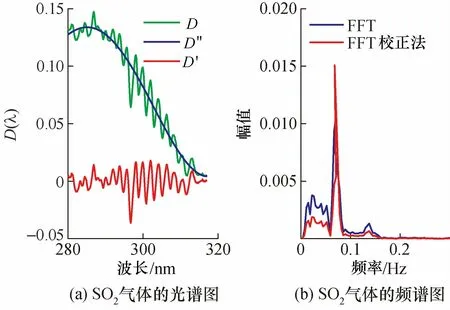
图2 SO2气体的光谱图和频谱图Fig.2 The spectrum and frequency spectrum of SO2

SO2气体是大气中的主要污染气体［14］，其特征吸收光谱具有很强的准周期性，如图2（a）所示。通过傅里叶变换，其频谱中的低频部分就是光谱密度的“慢变”部分D″（λ），高频部分就是“快变”部分D′（λ）。频谱能量集中在一个较小的频带范围内，选取频谱峰值点附近的几个频率点进行浓度反演，相当于进行了带通滤波，能有效抑制其他干扰气体的影响。傅里叶变换滤波法求气体浓度，就是对式（2）中D′（λ）和σ（λ）分别进行傅里叶变换滤波后，再反演气体的浓度。浓度c′的表达式为

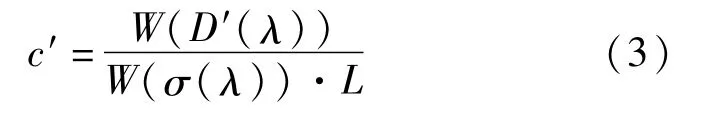
由于实验测量的频谱信号不可能无限长，频谱分析只能在有限区间进行。由于时域截断及分析个数有限，会造成能量泄露和栅栏效应［15，16］。使频谱的峰值减小，精度降低，产生较大误差，所以需要对离散频谱进行校正，其具体步骤［17］如下：

通过加Hanning窗，取特征吸收波段内的实测光谱进行分析。离散化Hanning窗的定义为

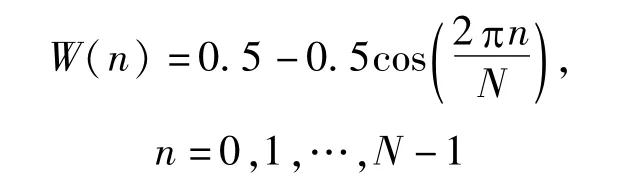
式中：N为分析点数，采样频率为fs时，频率分辨率为fs／N。

归一化加Hanning窗谐波信号的频谱主瓣函数：

通常主瓣内有4条谱线。设K为谱线序列号，利用谱峰主瓣内的两条谱线yK和yK－1求重心坐标x0：

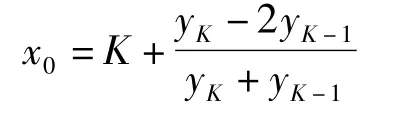
同理，有：

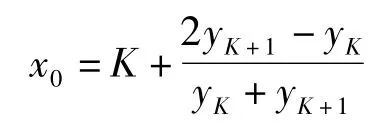
令x0＝K＋ΔK，得频率校正公式：

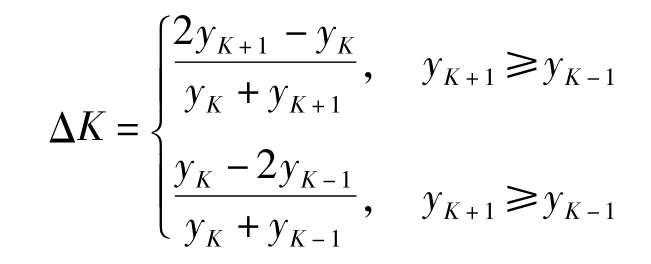
校正频率为：

将式（3）写成：

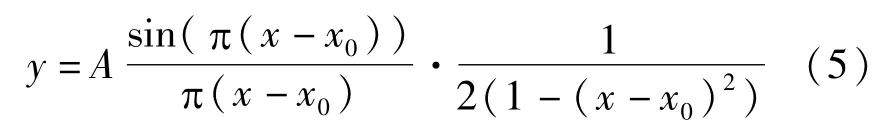
将y＝yK，x－x0＝K代入式（5），并求出校正幅值A为

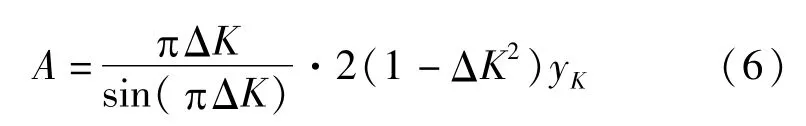
式中：yK为光谱信号加Hanning窗截断后的幅值谱的最大值。

对于式（6），在sin（πΔK）→0时，为了防止计算溢出，这时ΔK→0，ΔK→±1，有：

从式（7）可以看出，当ΔK→0时，即谱线对正主瓣中心时，幅值也需要校正。这是因为加Hanning窗使时域能量衰减的缘故。

傅里叶变换求气体浓度是利用频域的幅值信息，其相位信息对反演浓度影响不大，故舍弃对相位的校正。利用校正后的幅值，按照傅里叶变换滤波法，即可求出气体浓度。从图2（b）可以看出，在峰值点附近，FFT校正前后频谱的形状、位置没有发生较大的变化。这说明该算法没有引入新的误差，而校正后频谱的峰值明显增大，对FFT后的幅值进行了校正。

4 实验验证

4.1 实验装置

实验装置如图3所示，质量流量控制器采用七星华创生产的CS200D，准确度可以达到±1.0%S.P.（≥35%F.S.）。光源采用Avantes公司生产的脉冲氙灯AvaLight-XE。光源发出的光经石英透镜准直后，进入气体吸收池，再经石英透镜聚焦后耦合进光纤，并传输到光纤光谱仪AvaSpec-2048。光谱仪把光谱信号转化为电信号，由数据采集软件AvaSoft进行信号的采集和记录。

图3 实验装置图Fig.3 Schematic diagram of experimental system

4.2 结果与讨论

实验配备了7组不同质量浓度的SO2气体。选择280～320 nm光谱波段作为反演波段，光谱仪的采样间隔为0.14 nm。分别用最小二乘法、傅里叶滤波法和FFT校正法反演气体的浓度，实验结果见表1。

从表1可以看出，3种算法都取得较好的反演精度。随着SO2气体浓度的增加，3种算法的误差呈减小趋势，最大误差不超过4.2%。其中，最小二乘法浓度反演的平均误差为1.22%，FFT法的平均误差为1.74%，而经过离散频谱校正后，其误差进一步降低到0.86%。说明离散频谱校正法更适用于差分吸收光谱数据的处理。

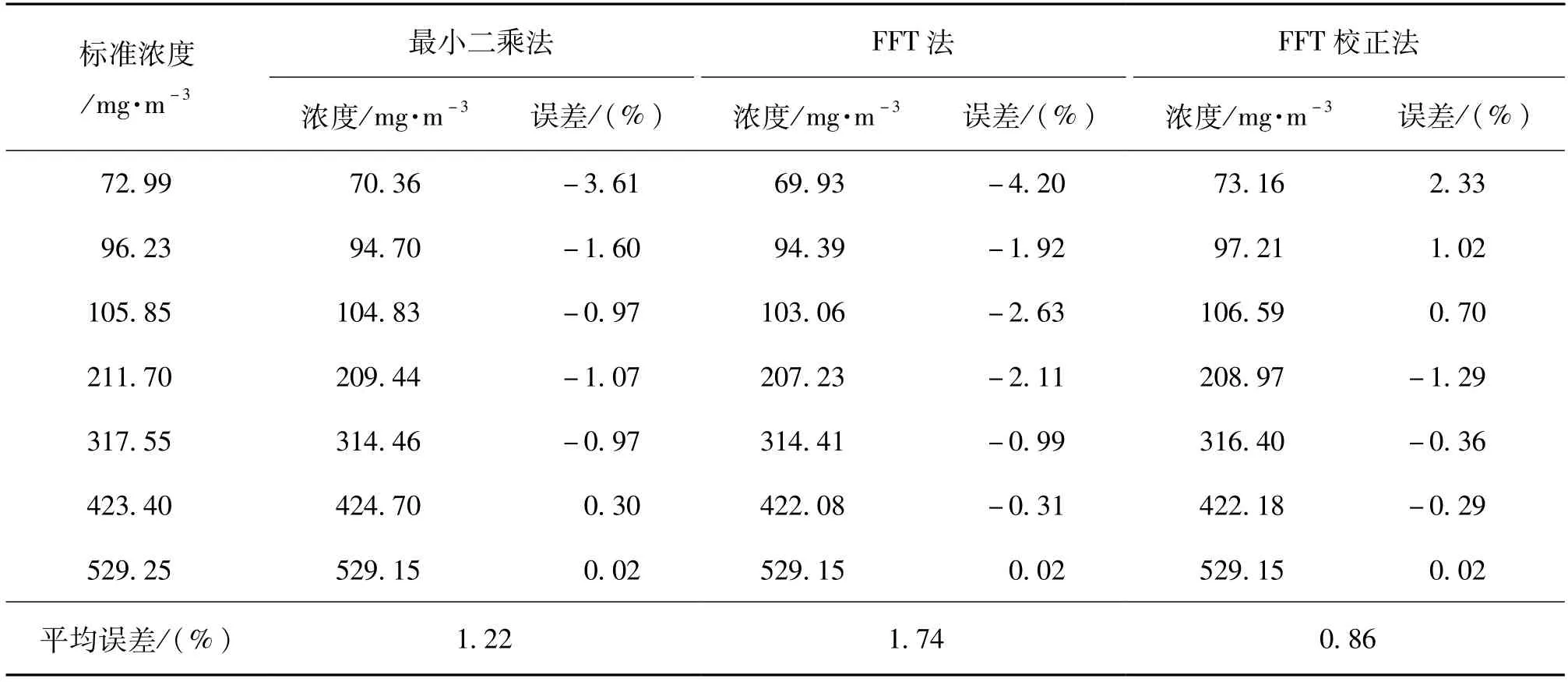
表1 不同浓度SO2气体的测量结果Tab.1 Measurement results of SO2 with different concentration

为了验证3种算法的稳定性，实验对同一浓度的SO2气体进行多次测量，并分别用3种算法反演浓度，其浓度误差曲线如图4所示。由图4可见，最小二乘法虽满足国家误差标准的要求，但相对于FFT滤波法和FFT校正法误差偏大，且误差波动较大。FFT滤波和FFT校正法均取得不错的反演效果，反演误差总体比较平稳，且FFT校正法的反演浓度误差小于FFT。

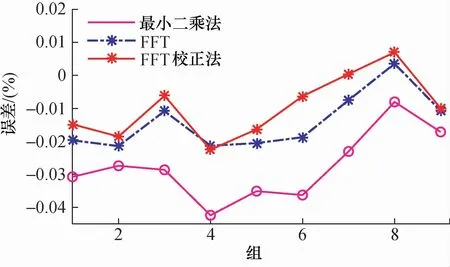
图4 同一浓度SO2气体的测量误差Fig.4 The measurement error of SO2 with the same concentration

针对相同浓度的SO2气体，实验模拟了光谱数据向长波长漂移两个采样间隔为0.28 nm的情况，如图5所示。

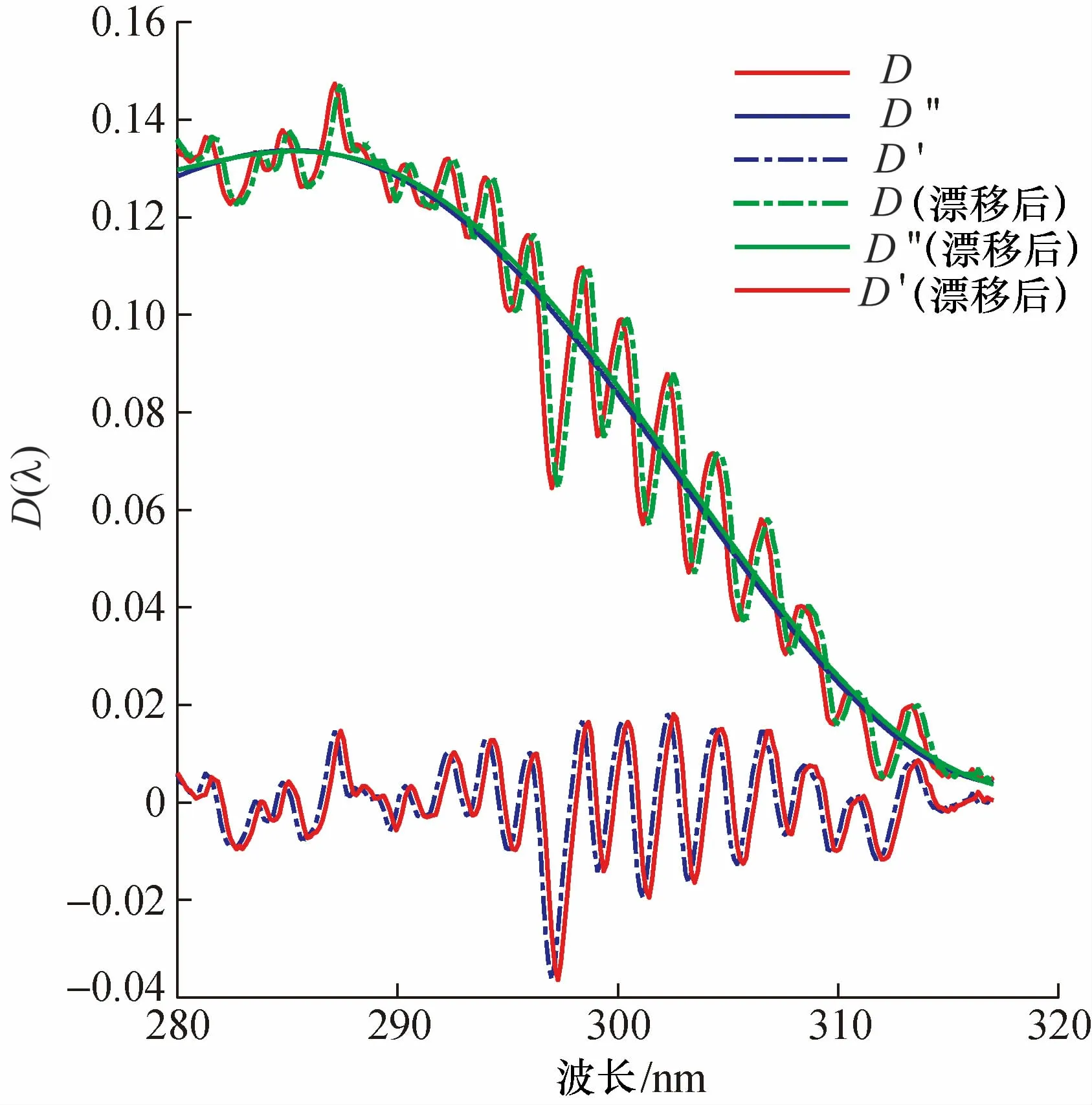
图5 谱线漂移光谱图Fig.5 The spectrum of SO2 with the drift

并对3种算法的反演误差进行了比较，结果见图6。

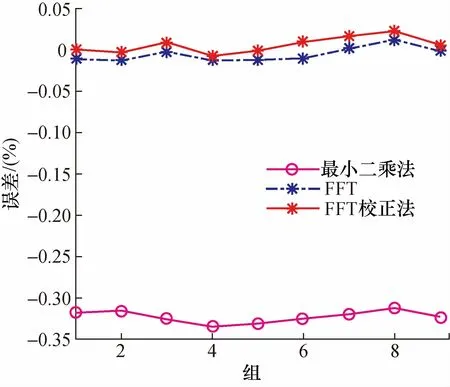
图6 谱线漂移2个采样间隔SO2浓度测量误差Fig.6 The measurement error of SO2 with the drift of two sampling intervals

最小二乘法的平均误差为31.8%，FFT滤波法和FFT校正法的误差均在5%以内，符合国标要求，且FFT校正法的反演精度优于FFT法。这是因为DOAS法测量气体浓度是根据光谱仪测得的差分吸收度和差分吸收截面进行拟合得到的。若出现谱线漂移，实测的光强已不是对应波长下的光强，还采用原来的差分吸收截面进行拟合，其反演的浓度值会出现较大的偏差。而FFT滤波法是在频域内进行，不考虑波长信息。当谱线漂移时，变换的还是同一组数据，只不过沿波长发生了移位，变换到频域后，其频谱图基本不变，如图7所示。所以差分光学密度和差分吸收截面在频域上的对应关系并没有改变，故谱线漂移对FFT滤波和FFT校正法的影响较小。

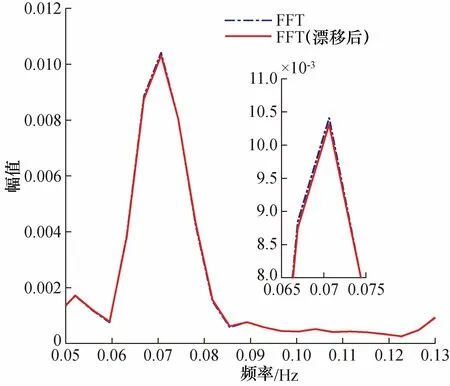
图7 SO2谱线漂移前后的频谱图Fig.7 The frequency spectrum of SO2

5 结论

本文提出了基于离散频谱校正的差分吸收光谱数据处理方法。分析了能量重心频谱校正法的原理，实验验证了能量重心法能够用于处理差分吸收光谱数据，且能获得较傅里叶变换滤波法更高的精度。模拟了实际可能出现的谱线漂移情况。实验结果表明：傅里叶变换滤波法能够有效滤除噪声，但由于频率分辨率的限制，在峰值谱线位于两谱线之间时，其幅值信息误差较大，使得反演精度受到限制。频谱校正FFT滤波法继承了FFT滤波的优良特性，同时对频谱进行了校正，进一步提高了反演精度；频谱校正法能有效排除谱线漂移的干扰，精度明显高于传统的最小二乘法。