几种笛卡尔积图的集合边染色
2021-09-09贾泽乐李沐春
张 明,贾泽乐,李沐春
(1. 兰州交通大学 电子与信息工程学院,兰州 730070;2. 兰州交通大学 应用数学研究所,兰州 730070)
1 引言
图染色是图论中的一个重要分支,在电路设计、交通运输和网络分析等方面都有着非常广泛的应用.图的染色理论有很多分支,其中包括点染色、边染色、全染色以及在此基础上添加其他约束条件所产生的一些特殊染色等.近年来,集合染色已经成为学者们关注的焦点.2009年,Hegde[1]提出了集合染色的概念,即给定图G的一个从点集V(G)到集合X中一个非空子集的映射f,其中X={1,2,…,k},k为正整数,如果满足对图G中任意的两个相邻的点u,v,有f(u)≠f(v),则称f是图G的一个集合点染色,并将集合X中包含颜色的最小数目k称为集合点色数,记为χS(G).2010年,Boutin等[2]定义了强集合染色的概念,即在满足集合染色的前提下,边的颜色是通过与其关联的两个顶点做对称差,同时集合X中的非空子集分别只在顶点和边上表现一次,同时他们对路和完全二叉树进行了研究,并得到了这两类图的强集合色数均不超过4.2011年,Balister等[3]通过对图进行点边划分,从而找到了几类满足集合染色的特殊图.王艳丽[4]研究了向日葵图和风车图的集合色数并给出了团数是3的平面图,没有4圈的平面图及烟花图的集合色数[5].2012年,王艳丽等[6]运用结构图论的方法,给出了集合边色数的下界以及图与其顶点删除子图、边删除子图的集合边色数的关系.2013年,王艳丽等[7]运用分析的方法证明了路与扇的笛卡尔积图的集合边色数等于图的最大度,同时她们猜想:任意图的笛卡尔积图的集合边色数都等于它的最大度.2019年,杨笑蕊等[8]研究了两类冠图的邻和可区别全染色.2020年,王鸿杰等[9]应用构造染色函数法和色集合分配法研究了圈、路、轮等图的集合点染色.贾泽乐等[13]得到了广义-Mycielski图的集合点色数,并得到了广义θ-图的集合边色数[14].2021年,贾秀卿等[15]运用数学归纳法并结合Hall定理研究了单圈图的D(2)-点可区别边染色,并得到了具体的边色数.
笛卡尔积图的染色问题是研究特殊图染色的一个重要方向.董秀芳[10]分四种情况对路与完全图的笛卡尔积图进行研究,并得到一些有趣的结果.王君帅等[11]利用函数构造法,研究并确定了由简单图构成的笛卡尔积图的强边色数.
在图染色研究中,利用染色函数来确定图的色数是目前最主要的工具之一.本文首先引入了集合矩阵,然后利用构造染色矩阵的方法给出圈与路、路与路、圈与圈的笛卡尔积图的集合边染色及其边色数.
设G(V,E)是由顶点集V(G),边集E(G)组成的简单连通图.其中Δ和δ分别表示G的最大度和最小度,d(u)表示点u的度数,n表示顶点的个数(阶数).用Pn和Cn分别表示n阶的路和n阶的圈图.下面引入两个图的笛卡尔积图的概念。
定义1[12]设G和H为简单连通图,其顶点集分别为V(G)={v1,v2,…,vm},V(H)={v1,v2,…,vn},则图G和H的笛卡尔积图G×H定义如下:
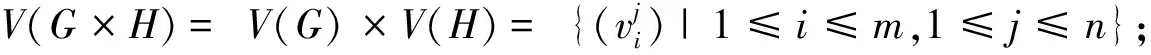
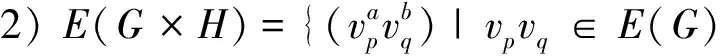
为了直观了解笛卡尔积的定义,给出P4和P5的笛卡尔积图(即图P4×P5),见图1所示.
此外,结合图的边染色、全染色和邻点可区别全染色引入图的集合边染色概念,具体如下:
定义2对于简单连通图G,令f是E(G)到集合X中非空子集的一个映射,其中X={1,2,…,k},k为正整数,如果满足:
1) 对∀uv,uw∈E(G)且v≠w有f(uv)≠f(uw);
2) 对∀uv,uw∈E(G)且v≠w有f(uv)∩f(uw)≠Ø.
则称f为图G的一个集合边染色,简记作图G的k-SEC,并将
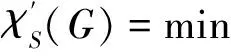
记为G的集合边色数.
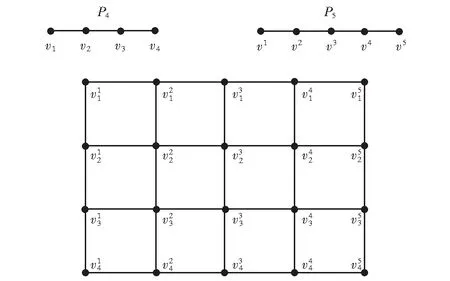
图1 P4×P5Fig.1 Graph P4×P5
2 主要结论
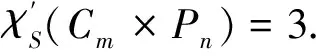
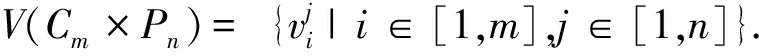
情况1当m≡1(mod 2),n≥2时
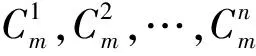
当1≤i≤m-1且1≤j≤n时:
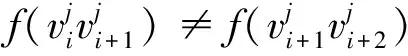
为方便表示,用n个m×1向量S1,S2,…,Sn所构成的集合矩阵S来表示n个不交圈Cm的3-SEC染色f:
S=(S1S2…Sn)=
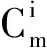
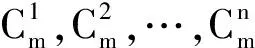
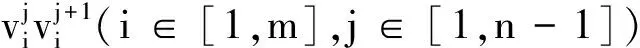
最后,得到一个染色矩阵如下:
(S1X1S2Y1…Sn-2X1Sn-1Y1Sn)
情况2当m≡0(mod 2),n≥2时,
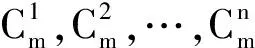
当1≤i≤m且1≤j≤n时:
为方便表示,用n个m×1向量T1,T2,…,Tn所构成的集合矩阵T来表示n个不交圈Cm的3-SEC染色f:
T=(T1T2…Tn)=
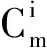
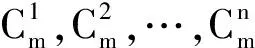
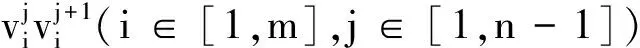
最后,得到一个具体的染色矩阵为:
(T1X2T2Y2…Tn-2X2Tn-1Y2Tn)
综上所述,结论成立.
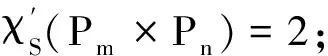
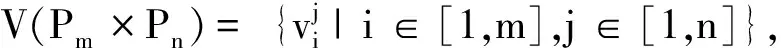
情况1当m=n=2时,P2×P2=C4.用集合{1},{1,2}依次循环对P2×P2中的边进行染色,于是得到了图P2×P2的一个2-SEC染色.
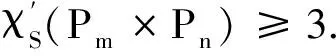
首先给出n条路中每条路Pm的一个2-SEC染色f,当1≤i≤m且1≤j≤n时:
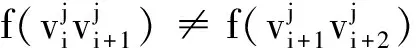
为了方便表示,用n个m×1向量U1,U2,…,Un所构成的集合矩阵U来表示n条不交路Pm的2-SEC染色f:
U=(U1U2…Un)=
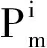
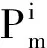
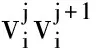
最后,构造具体的染色矩阵如下:
(U1X3U2Y3…Un-2X3Un-1Y3Un)
综上所述,结论成立.
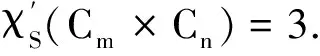
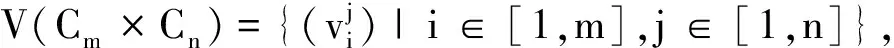
情况1当m,n≡0(mod 2)时,
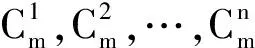
当1≤i≤m且1≤j≤n时,
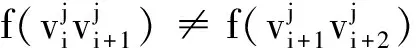
为方便表示,用n个m×1向量V1,V2,…,Vn所构成的集合矩阵V来表示n个不交圈Cm的2-SEC染色f.
V=(V1V2…Vn)=
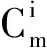
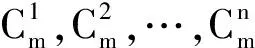
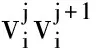
最后,经过整理得到具体的染色矩阵为
(V1X4V2Y4…Vn-2X4Vn-1Y4VnZ4)
情况2当m≡0(mod 2),n≡1(mod 2)时
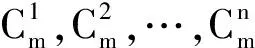
当1≤i≤m-1且1≤j≤n时,
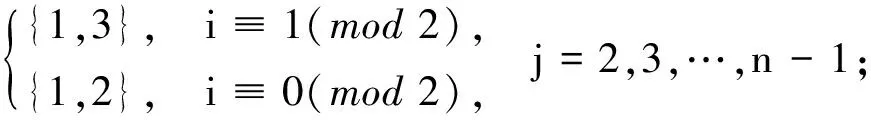
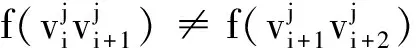
为方便表示,用n个m×1向量R1,R2,…,Rn所构成的集合矩阵R来表示n个不交圈Cm的3-SEC染色f.
R=(R1R2…Rn)=
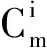
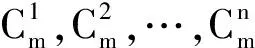
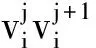
最后,经过整理得到具体的染色矩阵为:
(R1X5R2Y5…Rn-2X5Rn-1Y5RnZ5)
情况3当m≡1(mod 2),n≡0(mod 2)时
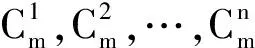
当1≤i≤m且1≤j≤n时,
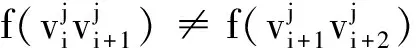
为方便表示,用n个m×1向量P1,P2,…,Pn所构成的集合矩阵P来表示n个不交圈Cm的3-SEC染色f.
P=(P1P2…Pn)=
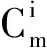
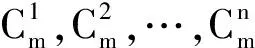
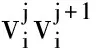
最后经过整理得到具体的染色矩阵为
(P1X6P2Y6…Pn-2X6Pn-1Y6PnZ6)
综上所述,结论成立.
