参数优化VMD对变压器声音信号的故障诊断
2021-09-09魏才懿马建桥
魏才懿,杨 军,马建桥
(1. 兰州交通大学 自动化与电气工程学院,兰州 730070;2. 兰州交通大学 测绘与地理信息学院,兰州 730070)
变压器的可靠性在电网的高效稳定运行中具有至关重要的作用,及时诊断出变压器的局部放电能有效预防其发生故障[1].目前,变压器内部局放故障的常用诊断方法主要有脉冲电流法[2]、超声法[3]和油色谱分析法[4]等,这些方法易造成变压器的二次损坏,而变压器声音信号蕴含了故障状态的重要信息,在一定程度上反映了变压器内局放故障情况,长期一线工作的检修员通过耳朵可以对变压器运行状况进行大致判断,但无法对其内部故障定性判断,这种普遍使用的诊断方法在很大程度上依赖于技术人员的主观判断和个人经验,具有很大的不确定性.但这一现象证明了利用可听声信号诊断变压器故障的可行性,借助于声音传感器和现代数字信号处理技术,可实现比人工更客观、更可靠的在线监测和故障诊断[5-6].由于变压器内部局放声音信号受传播介质影响,呈现出短时随机脉冲的特点,导致提取的故障特征不能充分表征故障样本,进而影响到故障类型识别的准确率.研究者一般采用小波包变换[7]、频率响应分析[8]等方法对故障信号进行处理.但这些方法都依靠人的经验来设置参数进行分解,对于复杂的局放声信号,可能会造成故障特征信息的丢失或冗余,使故障诊断的性能受到严重影响.故从声音信号中提取高质量的故障特征信息是整个故障诊断的关键.
变压器声音信号会伴随其内部绝缘故障放电时产生非线性非平稳性信号.为得到能够表征不同类型放电的有效特征信息,目前常用的放电特征提取方法有小波特征法[9-10]、经验模态分解(empirical mode decomposition,EMD)[11-12].小波特征法是基于小波分解的特征提取方法,实质上是一种傅里叶变换,需要选择适合的小波基和分解层数,并且不具备自适应性.EMD相对小波分解,不需要做预先分析与研究,自动按照一定固有模式按层次分好,虽然减少了人为干预和设置分解层数,但在分解过程中存在端点效应和模态混叠(一个单独的本征模态分量(intrinsic mode function,IMF)信号中含有不同的时间尺度)等问题.此外,Smith[13]提出局部均值分解(local mean decomposition,LMD)方法来改善EMD的缺陷,但该方法抗干扰能力差,受分解层数的影响容易出现不收敛等问题,和EMD一样LMD也受限于递归模式分解框架中.Dragomiretskiy等[14]于2014年提出变分模态分解方法,其利用非递归的技术对信号分解,通过引入变分模型,将信号分解问题转化为约束模型的寻优问题,可以实现各信号分量频率的分离,避免LMD及EMD存在的模态混叠等问题.
针对变压器故障声信号特征提取不佳而导致诊断识别率低的问题,提出模拟退火优化变分模态分解—样本熵(simulated annealing variational mode decomposition sample entropy,SA-VMD-SE) 的特征提取方法.VMD中分解层数K和惩罚因子α的选择没有规律,通常按研究者的经验选取,本文首先将模拟退火算法(simulated annealing,SA)[15]应用于两参数全局寻优,利用最优参数设置VMD分解故障声信号,得到反映不同频带特征的本征模态函数;其次求取衡量各分量复杂程度的样本熵作为表征故障样本的特征;最后将求得的样本熵作为SVM分类器的输入特征向量进行故障识别与诊断.
1 变分模态分解
变分模态分解[14]将一个原始信号f分解为K个IMF,第k个IMF分量的表达式为
uk(t)=Ak(t)cos(φk(t)),
(1)
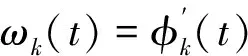
通过如下步骤计算每个IMF分量的带宽:
首先,对每个本征模态函数uk(t)进行Hilbert变换,计算模态函数的解析信号,即
(2)
其次,通过混合模态解析信号与预测信号中心频率e-jωkt,将每个模态的频谱调制到对应的基频带,如下所示:
(3)
最后,计算解调信号梯度的L2范数,估计各IMF分量的带宽后,为使得各分量的估计带宽之和最小,构造约束变分模型为:
(4)
VMD方法就是通过求解上述约束变分模型的最优解进而自适应地分解信号.通过引入二次惩罚因子α和Lagrange算子λ(t)(其中:α可以保证噪声条件下信号的重构精度;λ(t)确保约束条件保持严格性),将该模型的约束变分问题转化为非约束变分问题求解,如下所示:
(5)
利用交替乘子法(alternating direction method of multipliers,ADMM)不断更新各本征模态分量及其中心频率,最后所求上式的凸优化问题即为原问题的最优解.因此,可由式(6)得到所有本征模态分量.
(6)
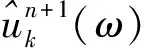
算法中各本征模态分量的中心频率更新公式如下:
(7)
以上即为变分模态分解全过程,从分解原理来看,VMD虽然规避了EMD的模态混叠问题,但其分解精度受分解层数k以及惩罚参数α的影响.现有对参数的取值往往根据先验知识,难以保证信号的最优分解,如文献[16]利用EMD分解后的分量频率来估计k值的选取,但由于EMD本身模态混叠和端点效应的缺陷,不可避免地会影响k值的结果.因此,寻找合适的参数值是保证变分模态分解的关键.
2 基于模拟退火算法的参数优化
上节分析了VMD算法过程中参数α和k对分解的影响,根据经验定参的设置方法得不到最优的分解效果,而模拟退火算法是Metropolis等[15]基于Monte-Carlo迭代策略提出的求解复杂组合优化问题的一种有效方法,其思想是基于晶体冷却过程与组合优化问题之间的相似性,通过接受赋予新状态的过程(一种时变且最终趋于零的概率突跳性),可有效规避陷入局部最优并最终趋于全局最优解,故本节采用模拟退火算法进行参数优化来得到最优参数组合.其主要步骤为:
Step1设定退火起始温度T0,冷却系数q,终止温度Tend和每个温度层T下的迭代次数L;
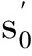
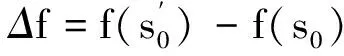
Step4在当前温度T下对Step2~Step3进行L次迭代循环;
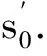
利用模拟退火算法确定VMD的参数时,Step2中需要一个目标函数f(s0),通过对比目标函数值的大小进行状态的更新.变压器局放故障声信号经过VMD后,若IMF分量中包含噪声较多,放电时的放电特征则会被掩盖,此时分量信号的稀疏性弱,包络熵较大;反之,若IMF分量中包含噪声较少,则会出现可能的放电冲击特征,此时分量信号的稀疏性强,包络熵较小,包络熵越小说明分量蕴含故障信息越丰富,也说明信号分解得越好.所以用分量包络熵作为参数寻优的目标函数,时间序列x(j)(j=1,2,…,N)的包络熵Ep定义为:
(8)
式中:pj是a(j)的概率分布序列;a(j)是序列x(j)经过Hilbert变换后得到的包络信号.
3 样本熵
熵为衡量时间序列复杂性的参量.样本熵(sample entropy,SampEn)是Richman等[17]提出的一种度量时间序列复杂性和统计量化的方法,其物理意义和近似熵类似,都是通过衡量序列嵌入维数变化前后时间序列产生新模式概率的大小说明信号的复杂度.评判原则为:不同维数下与相似容限度差别越大,产生新模式的几率越大,即熵值越大对应时间序列越无序;相反,若样本熵值越小,说明自我相似性越高,对应时间序列越规律.由于变压器局部放电发生时其状态会发生改变,即会产生不同的声音,故可以借助样本熵来计算不同局放故障时的信号复杂度.其计算过程如下:
设长度为N的一维时间序列{x(n)}=x(1),x(2),…,x(N),按序号组成一组维数为m的向量序列
Xm(1),Xm(2),…,Xm(i),…,Xm(N-m+1),
其中,Xm(i)={x(i),x(i+1),…,x(i+m+1)},1≤i≤N-m+1.这些向量表示第i点开始的m个x的值.
定义向量Xm(i)与Xm(j)之间的距离d[Xm(i),
Xm(j)]为两者对应元素中最大差值的绝对值,即
(9)
对于给定的Xm(i),统计Xm(i)与Xm(j)之间距离不大于参数r的数目j(1≤j≤N-m,j≠i),并记为Bi,则当1≤i≤N-m时,定义
(10)
定义Bm(r)为
(11)
将维数增加到m+1,按照上述公式计算Bm+1(r),这样得到的Bm(r)和Bm+1(r)是在相似容限r下分别匹配m和m+1个点的概率.此时该序列样本熵定义为
(12)
实际样本序列中N为确定值,样本熵定义为
(13)
4 基于SVM的变压器局放故障分类
在得到表征故障的有效特征样本熵后,需要一个准确的分类器对这些特征进行分类识别.支持向量机(support vector machine,SVM)是Vapnik等在统计学理论基础上提出的一种有监督学习方法[18],作为经典的决策算法,SVM在解决小样本和高维非线性分类问题中具有独特的优势和普适性,已经广泛应用到模式识别和故障预测等诸多领域[19-21].在非线性问题方面,SVM通过引入惩罚系数与核参数将其转化至高维空间的线性问题,从而实现准确分类,但参数的选择不同对SVM的分类效果也相差较大,目前许多学者采用智能优化算法进行SVM优化研究[16,22].综合考虑实验条件下样本少及SVM能解决高维非线性小样本等优点,本文选择经典的SVM作为变压器局放故障诊断方法.其原理如下:
假设训练集为{(xi,yi)},i=1,2,…,M,x∈Rn,yi={-1,1},其中:M为样本数;x∈Rn为输入的n维特征空间;yi表示输出的分类标签.假定类别是线性可分时,存在如下表达式:
yi(ω·xi+b)-1≥0.
(14)
则超平面表示为
fω,b=sign(ω·x+b).
(15)
因此,SVM模型的求解最大分割超平面问题又可以表示为以下约束最优化问题:
(16)
若线性不可分时,引入松弛因子ξi,则
(17)
对于非线性条件下的分类问题,通过核函数将特征向量x∈Rn映射到高维空间,转化为线性分类问题,其表达式如下:
K(xi,xj)=Φ(xi)·Φ(xj),
(18)
则式(15)可写成
(19)
式中,λi为拉格朗日乘子.
综上所述,本文通过模拟退火算法对VMD进行参数寻优,采用最优参数设定VMD对故障声音信号进行分解,求取分解后各分量的样本熵作为故障特征,将这些故障特征分为两部分,一部分作为训练数据训练SVM,另一部分作为测试数据验证SVM的识别分类结果,最终实现对故障类型的诊断.具体诊断流程如图1所示.
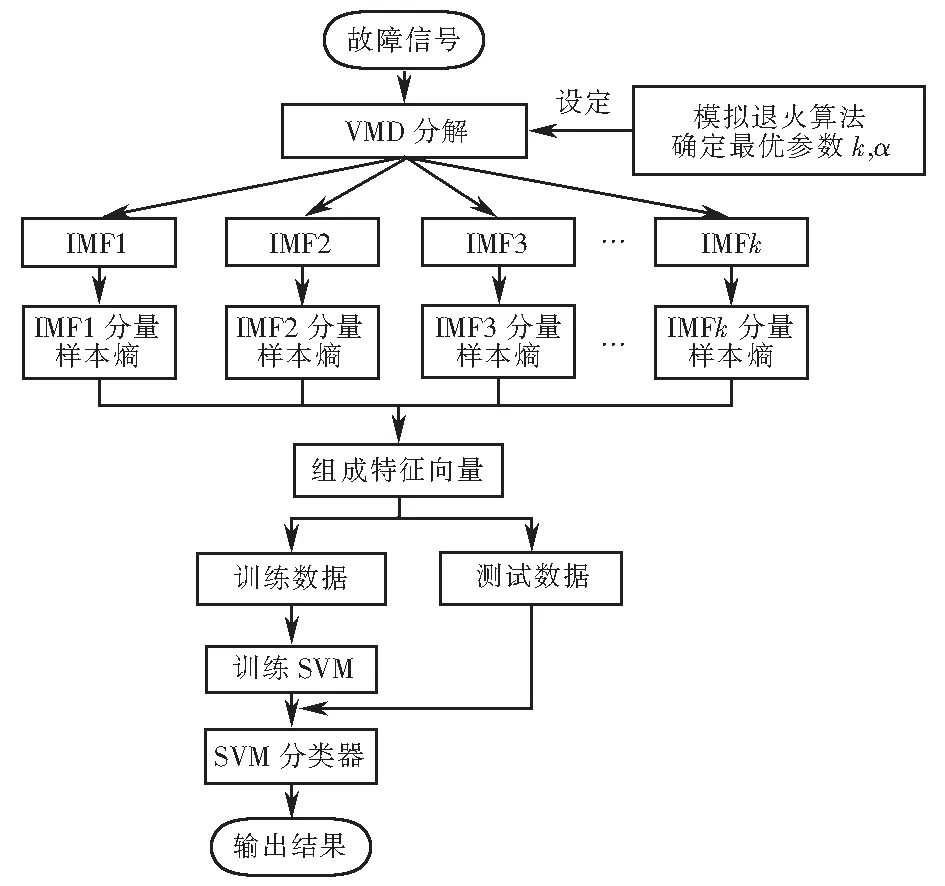
图1 变压器故障诊断流程Fig.1 Process of transformer fault diagnosis
5 试验分析
5.1 模拟信号分析
利用仿真信号来验证本文所提方法的有效性,设置采样频率为5 kHz,模拟变压器内部局放声音信号x(t),主要由50 Hz变压器基频信号x1(t)=cos(2π×50t),偶次谐波信号x2(t)=0.07cos(2π×100t)-0.05cos(2π×200t)+0.02cos(2π×300t),随机正弦脉冲信号x3(t)和一组信噪比为5 dB的高斯白噪声信号x4(t)叠加组成,模拟局放信号如图2所示.
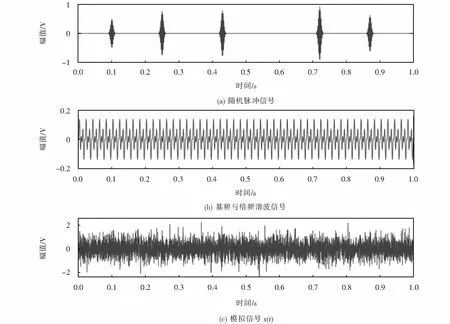
图2 模拟信号时域波形图Fig.2 Time domain waveform of simulated signal
设置寻优VMD参数范围k∈[5,15],α∈[100,3 000],模拟退火起始温度应选的足够高,使所有转移状态都被接受,因此起始温度与终止温度值分别设定为10 000 ℃和20 ℃,冷却系数q=0.95,通过多次迭代来找到对应温度下最好的解.最终得到最优参数k=5,α=1 800.图3为退火算法对VMD参数寻优结果图.
为验证分解效果,对模拟信号进行EMD分解得到各模态分量时频图,对比图4与图5可知,EMD分解后IMF7~IMF12与原始信号相关度不大,IMF1~IMF4信号模态混叠现象严重,存在虚假分量,对模拟脉冲信号的特征体现不够充分,而VMD在模拟退火参数寻优后,IMF2与模拟脉冲信号有较高相似度,充分体现了“故障”分量.
5.2 试验系统平台搭建
由于变压器运行中有很多干扰,为获取声信号而使用运行的变压器进行重复局部放电试验也不合理,因此,为验证本文方法的有效性,在油中局部放电平台上进行针板放电、沿面放电和气隙放电,模拟的3种变压器内部局放故障模型如图6所示,三种典型放电试验对应变压器内部实际放电故障如表1所列.
模拟局放试验系统由工频加压系统、变压器局放油箱模型和声音采集系统组成.局放试验采用IEC60270:200标准,声音信号经爱华传感器AWA14423采集,由于故障可听声频率在2 000 Hz以内[23],为保证采集到信号质量高保真,按照奈奎斯特采样定理,设置试验采样频率为5 000 Hz,然后通过前置放大器AWA14604以2 s为样本时长记录样本数据.试验中为减少水分对油纸模型绝缘介质的影响,事先使用烘干机对绝缘纸板充分烘干去除水分,然后浸泡48 h以备用[24].传感器安装在靠近油箱壁中心10 cm处.每种局放模型采集90组数据,在背景噪声极低的实验室环境下进行.实验电路原理如图7所示.
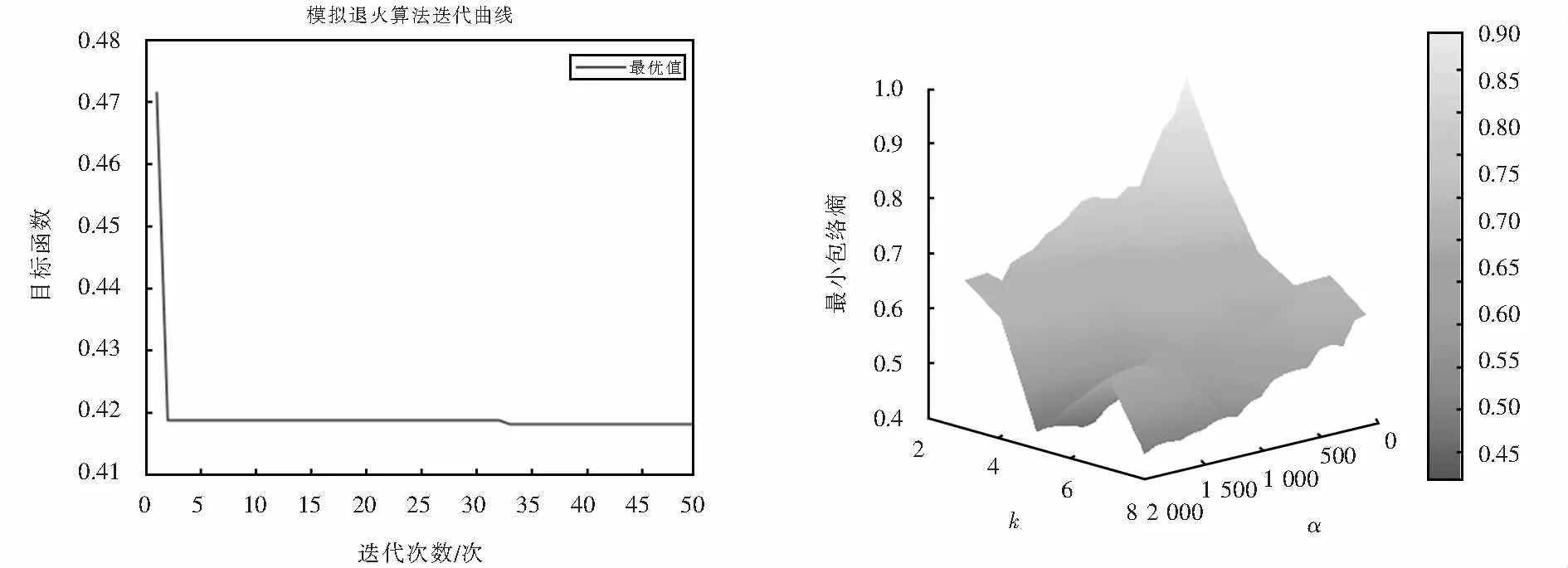
图3 模拟退火算法寻优结果图Fig.3 Optimization results of simulated annealing algorithm
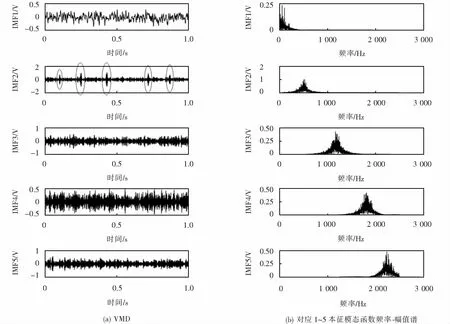
图4 模拟信号VMD分解时频图Fig.4 Analog signal VMD decomposition time-frequency diagram
5.3 仿真试验数据分析
针对以上试验系统采集到的3种局放信号,采用模拟退火算法寻优得到3种放电模型寻优迭代曲线与最优参数组合结果如图8所示.按优化结果最终设置变分模态方法的参数k=7,α=2 800,并分解所有信号;分解后计算样本熵作为特征量,设定其参数m=2,r为样本信号标准差的0.1倍,表2为3种放电信号分解后各样本熵的平均值,将表2绘制成折线图,如图9所示.
通过对表2和图9纵向比较可以看出,3种局放声音信号分解后的各IMF样本熵具有较为明显的差别,表示各模态分量在时间序列上的复杂度不同,较好地反映出了不同放电状态间的变化和差异,说明所提出的模拟退火优化变分模态分解—样本熵特征提取方法对局放故障声音信号特征具有可分性.
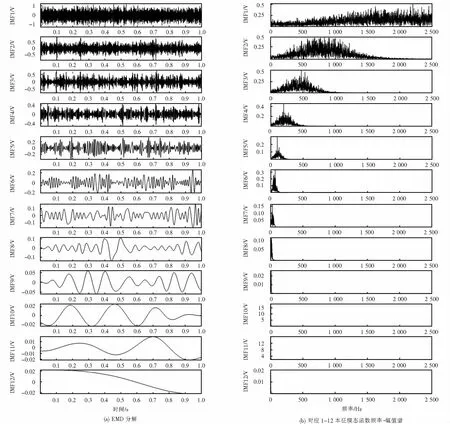
图5 模拟信号EMD分解时频图Fig.5 Analog signal EMD decomposition time-frequency diagram
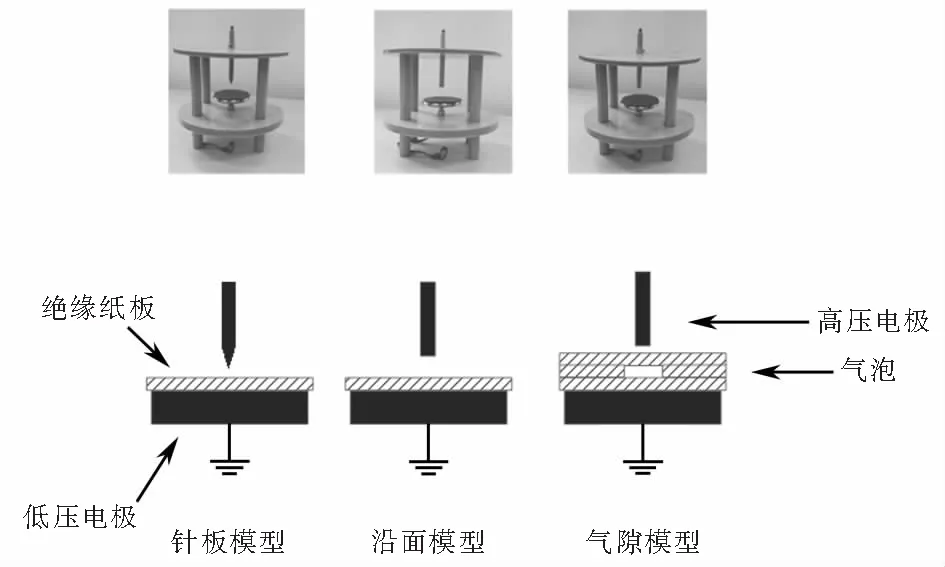
图6 3种变压器内部局放故障模型Fig.6 Three kinds of transformer internal local discharge fault models
为验证本论文方法的有效性及准确性,采用SVM识别不同放电声音信号,选取3种放电声音信号共270个样本(每种类型各90个样本),训练样本与测试样本按2∶1设定,故障对应类别标签为:针板—类别1、气隙—类别2、沿面—类别3,对SVM训练后测试样本识别结果如图10所示.从图10可以看出,90个测试样本中有7个样本没有准确分类,测试样本平均准确率为92.22%.

表1 三种典型局放故障模型对应变压器内部实际放电故障
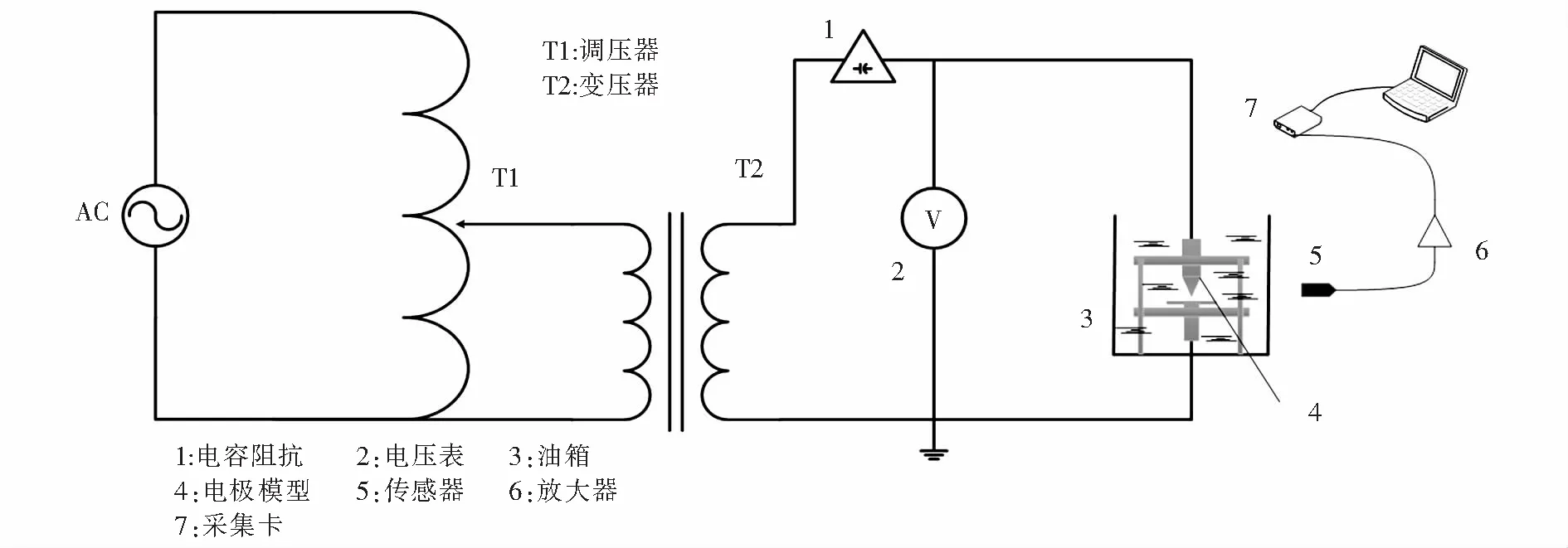
图7 实验电路原理图Fig.7 Schematic diagram of test circuit
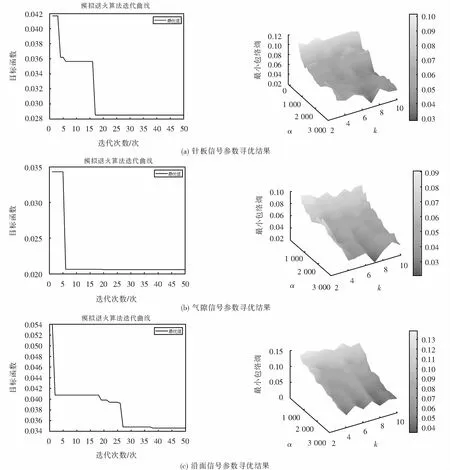
图8 3种模拟信号最优参数组合结果Fig.8 Results of optimal parameter combination of three analog signals

表2 3种放电信号分解样本熵平均值
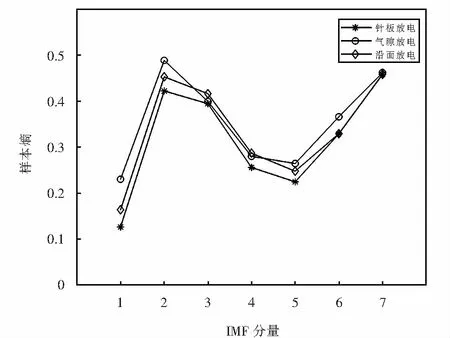
图9 3种放电信号分解样本熵平均值Fig.9 Average value of the three kinds of discharge signal decomposition sample entropy
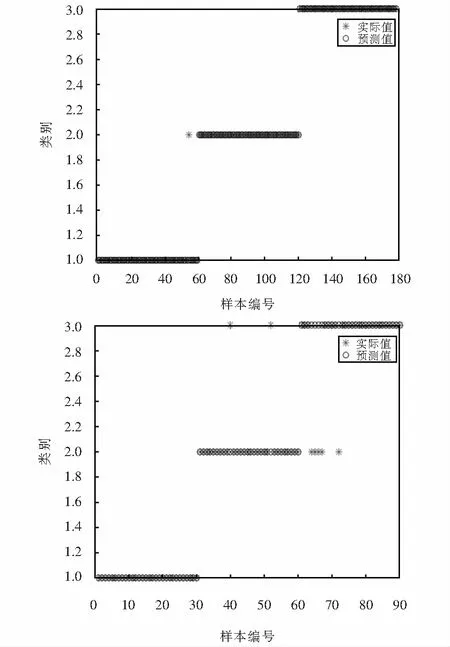
图10 识别结果图Fig.10 Recognition result graph
为进一步验证SA-VMD参数优化对故障模型声音信号分解的影响,将样本信号分别按EMD估计与中心频率估计后的k=6、9,α=2 000设置VMD处理信号,计算样本熵并识别,测试样本识别结果如表3所列.可以看出,SA-VMD分解后特征量的识别率达到92.22%,平均识别精度高于其他方法参数设定下的结果,说明模拟退火寻优后的VMD可以更好地分解并得到故障特征,而EMD估计法与中心频率估计法所得参数未能使VMD准确地分解信号,从而使不同类型故障特征量样本熵识别率不高.
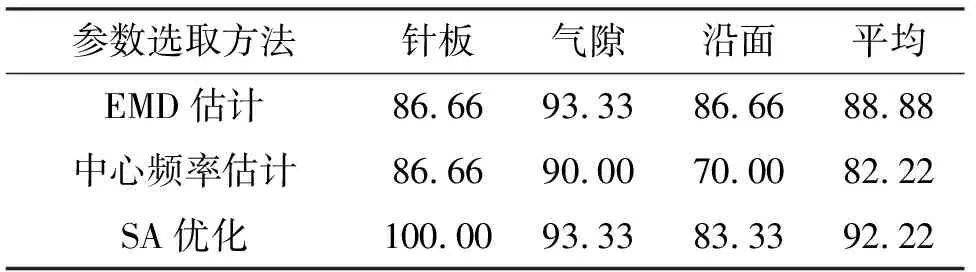
表3 不同参数选取方法下测试样本识别结果
6 结论
针对估计或给定参数的VMD对变压器放电故障声音信号分解不准确从而导致识别精度不高的问题,提出模拟退火优化变分模态分解—样本熵特征提取的诊断方法,得到以下结论:
1) VMD分解后各模态分量没有出现模态混叠等现象,对变压器放电故障模型信号分解较为清晰,可实现对3种放电模型声音信号的识别与分类.
2) 相比于EMD估计或给定参数的VMD,本文采用模拟退火算法对VMD参数寻优后,各本征模态分量的样本熵可以更准确地反映故障的状态变化,从而得到更好的诊断效果.
