别汉棱镜角度误差对光轴一致性影响的研究
2021-09-08杨加强彭晴晴杜晓宇
张 娟,杨加强,彭晴晴,王 希,杜晓宇
(中国电子科技集团第十一研究所,北京 100015)
1 引 言
在周视扫描成像系统中,探测器上接收到的图像会出现随着扫描而发生图像跟随轴旋转的像旋现象,影响系统正常成像。因此需要对所成的像进行处理或者对光学系统进行改进以达到消像旋的目的。对应的消像旋方法分别是利用图像处理等手段进行电子消像旋或者在光学系统中加入光学消像旋装置进行光学消像旋。前者消像旋的方式虽然结构简单,但获取图像信息有延迟,多用于对实时性要求不太高的仪器中[1-4];而后者能够及时获得图像信息。由于别汉棱镜具有如下优点:(1)别汉棱镜体积较小,结构紧凑,在比较短的实际距离内包含的光路特别长,从而大大缩小了整个系统的体积;(2)因为空气与玻璃交界面垂直于光轴,可用于会聚光路中。因此别汉棱镜被广泛地应用于消像旋系统中。在用别汉棱镜进行消像旋的系统中,如果对别汉棱镜的角度误差控制不严格,系统在工作时会出现光轴偏移或倾斜现象,影响系统使用,因此需要严格控制别汉棱镜的角度误差,保证出射光轴与入射光轴的一致性。国内外文献对于别汉棱镜胶合过程中三轴(光轴、机械轴、棱镜轴)不重合的误差已经做了非常详细的分析[5-7],但对于别汉棱镜自身角度误差的分析却很少提及。
本文首先推导了反射光线、折射光线和三维坐标系旋转的矢量形式表达式,建立了别汉棱镜角度误差模型,通过分析光线在别汉棱镜内的传播路径,并在Matlab中计算得到经过别汉棱镜之后出射光轴的方向向量及其相对入射光轴的偏差,通过光线追迹仿真的方法和实验论证的方法,验证了建立角度误差模型及理论计算的正确性,根据理论计算结果调整两棱镜之间的相对位置,使棱镜的出射光轴与入射光轴保持一致,缩短了棱镜胶合时间。
2 理论分析与推导
如图1所示,别汉棱镜由半五角棱镜Ⅰ和施密特棱镜Ⅱ组成。图中给出了光线在别汉棱镜内的传播路径,光线传播遵循反射定律和折射定律。因此,首先分析并推导折射光线和反射光线的矢量形式。
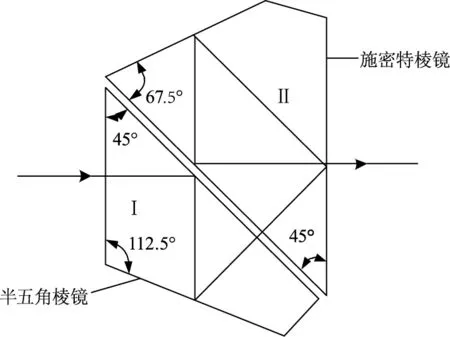
图1 别汉棱镜的组成Fig.1 Composition of Pechan prism
在棱镜的加工过程中,由于加工精度等其他因素的影响会产生很多误差。其中,对光轴一致性影响最大的误差是主截面内的角度误差和棱镜Ⅰ与棱镜Ⅱ交界处的棱的几何位置误差。当光线传播到存在几何位置误差的表面时,该表面的法线向量是空间向量,光线与该表面法线的夹角是空间角,法线是绕该表面在主截面内的投影旋转得到,因此需要推导坐标系旋转的矢量形式表达式。
2.1 反射光线的矢量形式推导


图2 光的反射与折射的矢量形式示意图Fig.2 Schematic diagram of the vector form oflight reflection and refraction
根据反射定律可知,入射光线和反射光线位于同一平面内,反射角与入射角相等,即法线是入射光线和反射光线的角平分线,因此反射光线的矢量形式可表示为公式(1):

(1)
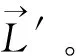
2.2 折射光线的矢量形式推导

(2)

(3)
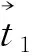
(4)
(5)
根据图2所示的向量之间的关系,可以求出:
(6)
将公式(6)代入公式(4),可以得到:
(7)
(8)
因此,折射光线的方向向量为:
(9)
2.3 三维坐标系旋转的矢量形式推导

图3 坐标系旋转模型Fig.3 Coordinate system rotation model
最终推导出的旋转矩阵M的表达式如公式(10)所示:
(10)
则Q点的坐标可用公式(11)求出:

(11)
3 别汉棱镜角度误差模型与光轴一致性计算
对别汉棱镜进行胶合时,通常在物方放置一台自准直仪,发射“十字叉丝光源”,当别汉棱镜存在角度误差时,从棱镜的AB面、AD面、EF面和EH面会反射回“十字叉丝光源”的像,这些不重合的像反映了出射光轴与入射光轴之间的偏差,即光轴一致性。通过在半五角棱镜Ⅰ和施密特棱镜Ⅱ之间的空气间隙填充垫片,调整半五角棱镜Ⅰ和施密特棱镜Ⅱ的相对位置,使得这些像重合在一起,此时出射光轴与入射光轴保持光轴一致性,既不偏移也不倾斜[8]。这样,当棱镜在系统中旋转时,出射光轴的方向向量将不会改变,像也不会发生摆动,从而实现消像旋的目的。
为了便于棱镜胶合,需要知道别汉棱镜存在不同的角度误差时,从棱镜各个表面反射回来的出射光轴与入射光轴之间的偏差,由于棱镜的角度误差对出射光轴的影响并不能通过简单的几何关系求得,因此需要对别汉棱镜进行建模,分析推导光线经过棱镜每个表面的法线的方向向量和出射光线的方向向量,经过计算求出由角度误差引起的出射光轴的方向向量及其与入射光轴之间的夹角,即可得知出射光轴相对于入射光轴的偏差。
在第2节中介绍并推导了分析棱镜角度误差需要用到的相关理论,本节在此理论的基础上,对别汉棱镜进行建模,并定量分析别汉棱镜的角度误差对出射光轴与入射光轴的光轴一致性的影响。
定义半五角棱镜的第一和第二角度误差分别是θ1和θ2,施密特棱镜的第一和第二角度误差分别为是θ3和θ4,其中,第一角度误差主要是针对主截面内的45°角而言,第二角度误差是针对两个斜面相对于主截面的垂直度而言,规定角A和角E小于45°时的角度误差为正值,按图中所示的主截面与垂直于主截面的表面的角度小于90°时的角度误差为正值。建立如图4所示的别汉棱镜角度误差模型,当别汉棱镜存在角度误差时,AD面的法线为空间直线,经过AD面的反射光线不能通过简单的几何关系推导得出。因此需要建立空间坐标系模型,根据光线与每个表面的关系和第2节中的相关理论,即可求得由角度误差引起的出射光轴的方向向量及其与入射光轴之间的夹角。

图4 别汉棱镜角度误差模型Fig.4 Pechan prism angle error model



Matlab是一款非常强大的数学软件,它的基本数据单位是矩阵,可以进行复杂的矩阵运算,上述计算过程的每一步都涉及到矩阵,且最终结果不能通过一个简单的表达式来概括,只能通过逐层计算,因此,选择Matlab对出射光轴的方向向量及其相对于入射光轴的偏差进行计算。表1给出了别汉棱镜不存在角度误差、存在单一角度误差和存在所有角度误差的情况下,入射光轴经过棱镜之后出射光轴的方向向量及其相对于入射光轴的偏差的理论值,其中,最后一列数据的角度误差值(θ1,θ2,θ3,θ4)=(3.6″,-10″,10.8″,-10″)为实际实验测得的角度误差数据,表2给出了入射光轴经表面AB、AD、EF和EH反射回物方的出射光轴的方向向量以及与入射光轴之间的偏差的理论值。表格中与x和y轴的偏差的正负与向量所在象限的正负一致。

表1 入射光轴经棱镜之后出射光轴相对于入射光轴的偏差的理论值Tab.1 The theoretical value of the deviation of the incident opticalaxis from the incident optical axis after passing through the Prism

表2 入射光轴经棱镜不同表面反射回物方的出射光轴相对于入射光轴的偏差的理论值Tab.2 The theoretical value of the deviation of the incident optical axis from the incident optical axiswhen the incident optical axis is reflected back to the object by the different surfaces of the prism
4 仿真分析与实验验证
为了验证建立的误差模型及计算结果的准确性,设计了一个对称光学系统,如图5所示,光学系统焦距为95.2 mm。当一束有发散角的光线经过光学系统之后变成准直光线进入别汉棱镜,经过理想别汉棱镜之后以准直光束出射,再经过对称的光学系统成像在像面上。

图5 对称光学系统光路图Fig.5 Optical path diagram of symmetrical optical system
将设计好的光学系统导入LightTools中,如图6所示为光学系统在LightTools中的模型。在系统物方设置“十字叉丝光源”,改变别汉棱镜的角度误差,设置每个光学元件的材料属性和表面属性,为了能看到反射回的“十字叉丝光源”的像,设置光线功率阈值为1×10-6W,追迹100万根光线,“十字叉丝光源”经过光学系统之后所成的像如图7所示,由于角度误差导致光线从表面AD、EF和EH反射回来的像如图8所示,根据像的位置可以计算出出射光轴相对于入射光轴的偏差,表3为经棱镜正常光路折反射之后的出射光轴相对于入射光轴的偏差的仿真值,表4为从不同位置反射回的出射光轴相对于入射光轴的偏差的仿真值。其中,Δx和Δy分别为像在x方向和y方向的偏移量,θx和θy分别为像与x轴和y轴的偏差;θ为出射光轴与入射光轴之间的夹角。

表4 入射光轴经棱镜不同表面反射回物方的出射光轴相对于入射光轴偏差的仿真值Tab.4 The simulated value of the deviation betweenthe incident optical axis and the incident optical axiswhen the incident optical axis is reflected back to theobject from different surfaces of the Prism

图6 光学系统在LightTools中的模型Fig.6 The model of the optical system in LightTools

图7 光源经棱镜正常光路折反射所成的像Fig.7 The image formed by the refraction and reflection ofthe light source through the normal optical path of the prism
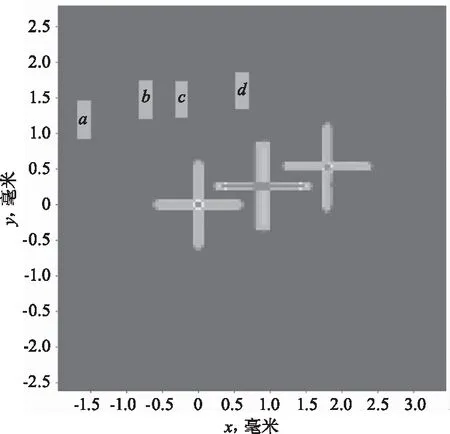
图8 光源经棱镜不同位置反射所成的像Fig.8 The image formed by the light source reflected atdifferent positions of the Prism

表3 入射光轴经棱镜之后出射光轴相对于入射光轴偏差的仿真值Tab.3 The simulation value of the deviation of theincident optical axis from the incident optical axis afterthe incident optical axis passes through the Prism
在LightTools中通过光线追迹的方法可得知:在图8中,a、b、c、d分别为光源经表面AB、表面AD、表面EH、表面EF反射回来的像,b和c重叠。
对比表1~表4,可以得出:通过成像仿真的方法得到的仿真值与通过建模计算得到的理论值相吻合,这说明第3节建立的模型以及计算推导过程是正确的。因为从仿真结果图中读取偏移量时有误差,因此,仿真值与理论值不能完全重合。
依据上述理论,对别汉棱镜胶合过程进行指导,用两台自准直仪使其光轴重合,其中一台平行光管的像与另一台平行光管的分划板重合,首先固定棱镜Ⅰ,并进行自准直,再放置棱镜Ⅱ,在两棱镜之间的空气间隙放置垫片,实验所得从棱镜不同表面反射回的“十字叉丝光源”的像的位置如图9所示,图9和图8所示的“十字叉丝”的位置相一致,说明上述仿真结果与建立的角度误差模型及理论计算是正确的。根据理论计算结果,调整棱镜Ⅱ的相对位置,最终使得四个“十字叉丝光源”的像重合在一起,此时,棱镜出射光轴与入射光轴一致,既不偏移也不倾斜。以此为零位,将整个棱镜翻转180°进行测量,测量结果为:出射光轴与入射光轴的重合精度为24.57″。图10为反射的“十字叉丝”重合之后经棱镜正常折反射之后所成的像。

图9 从棱镜不同表面反射的“十字叉丝”的像Fig.9 The image of "cross hairs" reflected fromdifferent surfaces of the Prism

图10 经棱镜正常折反射之后的像Fig.10 The image after normal refraction and reflection through a prism
5 结 论
为了提高别汉棱镜胶合效率。本文首先分析并推导了反射光线、折射光线和三维坐标系旋转的矢量形式表达式,在这些理论推导的基础上,建立了别汉棱镜角度误差的数学模型,推导出入射光轴经棱镜折反射之后的出射光轴的方向向量和入射光轴经棱镜不同表面反射回物空间的出射光轴的方向向量,并在Matlab中实现出射光轴相对于入射光轴的偏差的计算。在LightTools软件中通过光线追迹的方式仿真别汉棱镜成像,论证了建立模型及理论计算的正确性,通过实验进一步验证了仿真结果与理论分析计算结果是正确的,根据理论计算结果调整两棱镜之间的相对位置,使四个十字叉丝互相重合,此时测量得到出射光轴与入射光轴的光轴一致性为24.57″,缩短了棱镜的胶合时间,提高了棱镜的胶合效率和光轴一致性精度。
