引入探测器特性的空间目标红外灰度序列仿真研究
2021-09-08于秉志卢焕章陶华敏肖山竹
于秉志,卢焕章,陶华敏,肖山竹
(国防科技大学电子科学学院,湖南 长沙 410073)
1 引 言
红外探测技术凭借作用距离远、抗干扰性好和可全天候工作等优点,在空间探测系统中起到了重要作用。红外目标的识别算法研究需要良好的数据支持。由于空间目标和探测器距离遥远,直接观测的成本过高,易受到观测环境的影响,研究者们往往利用仿真得到实验数据。
对于几百公里外的空间远距离目标,红外探测器接收的红外辐射能量较小,目标成像为点目标。单帧图像无法直接获取目标形状及运动信息,从多帧图像中提取的点目标灰度序列可反映辐射强度的变化,可分析出目标飞行的状态和特性,因此利用序列进行目标识别是一种更为可行的方法。目标的红外辐射计算是红外仿真系统的基础。文献[1]~[2]综合了目标的轨道和飞行姿态,以及表面温度分布计算得到目标飞行的辐射强度序列,但并没有考虑探测器运动对观测造成的影响。文献[3]~[5]在前人工作的基础上,考虑了探测器和目标的相对运动对观测的影响。但相对于完整的红外探测系统,这些算法未考虑探测器自身的光学成像特性和探测器转换电路对于输出信号的影响,真实性较差。文献[6]~[8]在考虑了轨道运动,目标微动和表面温度分布等特性的同时,在仿真系统中加入探测器自身成像效应,提高了仿真的真实性,但未考虑目标微动特性对观测的影响。
本文综合分析了影响目标红外辐射的各种因素。分析目标和探测器的轨道运动,并结合目标的微动特性计算不同目标在探测器上的投影面积,综合目标温度变化计算得到目标红外辐射强度序列,并在仿真时加入探测器的成像效应和噪声,将辐射强度转化为灰度,构建了更接近真实场景的红外灰度序列信号仿真模型。本文将从空间目标观测系统,目标辐射特性和探测器成像三个方面,对仿真模型进行说明。
2 空间目标观测系统
一个完整的红外探测系统包括了红外光学系统,放大电路和显示器。红外光学系统来接收目标的红外辐射强度,再经由放大电路将像元接收的辐射强度转化为灰度,最终在显示器上呈现为红外图像。光学系统对目标的观测示意可见图1,目标发射的红外辐射经过光心传递到焦平面上的像元成像,远距离目标成像为单像素点,即为图中的P点。
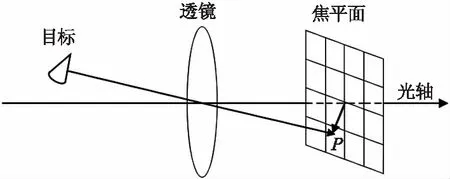
图1 目标观测示意图Fig.1 Target observation model
空间远距离目标的整个运动过程穿越了两次大气层,当运动于大气层外,环境接近真空,可忽略大气对于辐射传播的吸收和对探测器成像的影响,是本文的仿真情形。为便于分析,探测器的运动采用经典引导律中的追踪法,即运动方向始终指向空间目标。整个仿真系统利用三维直角坐标系进行计算,定义宏观的地球坐标系是以地心为原点,地心到北极点的连线为z轴,地心至赤道和零度经线交点连线为x轴,y轴依据右手定则得到。
3 空间目标红外辐射特性
3.1 空间目标运动
空间目标的运动轨道包含了坐标和观测距离等信息,是红外辐射的计算基础。在大气层外飞行的目标运动轨迹可简化为受到地球引力的椭圆平面运动,运动轨迹如图2所示。

图2 目标轨道运动示意图Fig.2 Schematic diagram of target orbital motion
其中,Oe表示地心;O为椭圆轨道中心;r是地心指向目标的矢量;f表示椭圆轨道的真近点角,即r和地心指向椭圆轨道近地点向量之间的夹角,v是目标速度矢量。根据动量矩守恒和万有引力定律可得目标运动公式[9]:
(1)
(2)
其中,r表示目标和地心的距离;e是椭圆轨道的偏心率;P是整个椭圆轨道的半通径;μ为地球引力常数,取3.986005×1014m3/s2。由以上公式可求得任意时刻和位置目标的坐标和速度。
3.2 空间目标投影面积
探测器在接近目标的过程中,探测距离的减小和目标的微动会导致目标在探测器上的投影面积变化。目标在被释放前会被赋予自旋角动量来保证稳定飞行[4],释放时受到冲击力的影响运动方式变为进动。对于轴对称分布的目标而言,整个进动可分解为自旋和锥旋运动的组合[10]。以圆锥目标为例,进动示意如图3所示。

图3 目标进动示意图Fig.3 Target precession diagram
图3中坐标原点为圆锥高的中点。自旋角速度为ωs,锥旋角速度为ωc,锥旋轴为角动量L,方向为目标的运动方向。自旋轴和锥旋轴之间的夹角为进动角θ。投影面积的计算可利用微元法将目标表面用三角面元分割法[3]分解为多个面元计算后累加,任意时刻目标表面对探测器的投影面积Aproj(t)计算公式为:
(3)
式中,ai是单个面元的面积,nl′为探测器的视线方向向量,ni′为面元表面法向量,此处两个向量是在同一坐标系下的表示,在各自的局部坐标系下的表示为nl和ni。仿真时探测器的局部坐标系和地球坐标系保持一致。可将探测器坐标系转换至目标局部坐标系来计算夹角的余弦。
如图4所示,Oduvw是探测器的局部坐标系,Otxyz为目标的局部坐标系。nl在目标局部坐标系上的单位向量表示可由与坐标轴的三个夹角γ1,γ2,γ3的余弦共同决定,计算的表达式为n′l=[cosγ1,cosγ2,cosγ3],在t时刻各个余弦的计算公式为[4]:
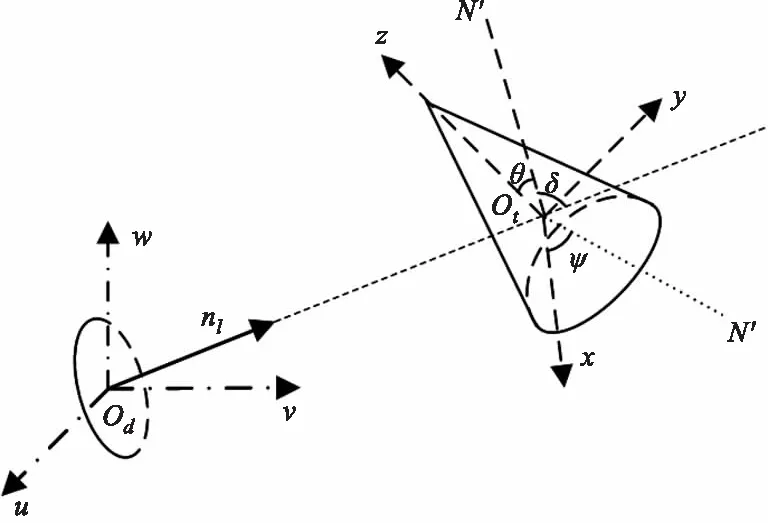
图4 探测器和目标局部坐标系示意图Fig.4 The local coordinate system of the detector and target
(4)
其中,δ为观测角,即地球坐标系下nl和锥旋轴ON的夹角,锥旋轴的方向向量为目标的运动方向;ON′是ON在xOty平面上的投影,设ψ0是ON′与x轴正方向的初始夹角;ωs为自旋角速度,ωc为锥旋角速度,有:
(5)
φ(t)为ON和z轴以及nl组成的两个平面之间的夹角。目标被释放时会有舱体碎片的产生,碎片发射的红外辐射也会被探测器接收,影响算法识别。碎片的运动可视为角速度大小恒定的自旋翻滚。弧形碎片在观测时存在着内表面被遮挡的情况,因此整个投影面积Aproj可以分为外表面投影面积Aout,内表面投影面积Ain和遮挡面积Acov三部分,如图5所示。
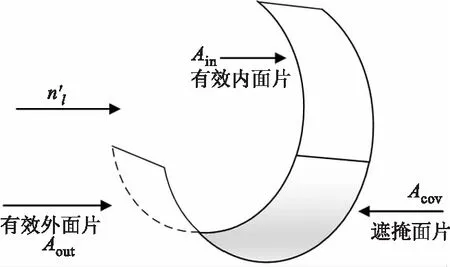
图5 弧形碎片投影面积示意Fig.5 The projection area of the arc fragment
碎片的投影面积计算公式如下:
Aproj=Aout+Ain-Acov

(6)
其中,Λin和Λout是内表面和外表面的有效面元集合,判别公式为:
(7)
Λcov是被遮挡的面元集合,计算需要确定两个面元之间的关系,若面元i和面元j之间某两点的向量nij若和n′l之间夹角小于设置的阈值,则可视为面元i为Λcov中的元素。
3.3 辐射强度
目标表面的材料形状会影响温度变化规律,表面温度变化及分布是影响目标辐射的一个重要因素[3]。目标的红外辐射接收和发射示意图如图6所示。

图6 目标红外辐射组成Fig.6 Target infrared radiation composition
分析时仍采用微元法,对于单个面节点i,由能量守恒定律可得热平衡方程表达式:
(8)
等式左边为节点吸收的热辐射,右边两项为节点发射的辐射。其中,c和ρ分别表示材料的比热容和密度,Ai,di,Ti分别表示节点的表面积,厚度和表面温度,t代表时间。Q1~Q4分别表示节点直接吸收的太阳辐射,地球红外辐射,地球反射的红外辐射,目标内部热源辐射,Q5表示节点之间的热交换;Q6表示节点i吸收的其他节点红外辐射,本文考虑的目标为凸面体在计算时该项为0;Q7表示节点自身向外的红外辐射。Q1至Q7的具体计算公式可参考文献[5]。在实际仿真中,由于识别算法要求要在尽可能短的时间内收集数据完成识别,目标表面温度分布可视为线性变化。
综合考虑上文提到的目标温度,轨道运动和投影面积等因素,可构建目标的辐射强度序列计算模型。假设目标为漫反射体,可由灰体辐射公式计算目标红外辐射强度的函数为:
(9)
其中,R(t)是探测器和目标之间的距离;D为探测器的直径;Aproj(t)为投影面积;E(T(t))是面片在单位立体角内波长在λ1至λ2范围内的辐射功率,计算公式为:
(10)
其中,ε(λ,T)是目标材料在λ波长时的红外辐射率;Mλ(T)为温度为T的黑体在单位表面积的辐射出射度,由普朗克定律计算可得到:
Mλ(T)=2hc2/λ5[exp(hc/(kλT))-1]-1
(11)
其中,c为光速大小为299,792,458 m/s;h为普朗克常数,大小为6.62606876×10-34J·s;k为玻尔兹曼常数,大小为1.3806503×10-23J/K。
4 探测器成像特性
目标发射的红外辐射被探测器接收时,信号会受到探测器自身的成像效应影响而改变。本文仿真的探测器类型为凝视阵列成像的非制冷型红外焦平面型。下面对探测器自身的成像效应进行分析。
4.1 焦平面成像弥散
理想的光学系统对于远距离目标成像为单个像素点,但实际会存在着光学系统的衍射、像差和离焦等效应的影响而使能量有扩散[11]。本文仿真只考虑衍射,在焦平面上的点目标成像衍射效应可以采用点扩散函数来描述,像平面任意位置的幅度响应表达式为:
(12)

(13)
其中,(u,v)是所求像元相对于成像中心像元的行列坐标,d为像元间的中心距。本文仿真计算3×3区域的像元幅度响应,用区域的灰度平均值来表示成像目标点的最终灰度值。
4.2 探测器像元的非均匀性
探测器对接收的单位辐照功率产生的输出电压或电流大小称为响应率,不同的探测器输入和偏置电路的设置会有不同的响应率[12],电压响应率Rv=Vs/P单位为(V/W),电流响应率RA=Is/P单位为(A/W),其中P表示探测器像元接收的辐照功率。探测器的输出电路采集每个像元的电压,将其量化为[0-255]范围的灰度值并显示。设输出电压最大值为VH,最小值为VL,用均匀线性量化,则电压V的灰度转换公式为:
(14)
在理想情况下,探测器上每一个像元对于辐射照度的响应率是相同的,可实际会因为制作工艺的影响造成像元响应的非一致性。这里不考虑红外光学系统带来的影响,也不考虑读出电路噪声。探测器的输出响应在短时间内可视为一阶线性函数,实际输出和真实响应的关系可表示为:
Y(i,j)=G(i,j)X(i,j)+O
(15)
i,j是像元的位置;X表示像元对辐照功率真实响应值;Y代表实际输出;G和O代表增益和偏置。仿真时非均匀性体现在增益的不同。每个像元的增益为αk,k为正常的电压灰度转换率,可由公式(14)计算得到。调节因子α服从均值为1,方差为0.1的高斯分布。
4.3 探测器盲元与噪声
红外探测器会受到半导体材料的不一致性和使用环境等因素的影响,在显示成像时会出现盲元。盲元在图像中表现为灰度不变化。仿真所模拟的探测器为GWIR 0303X2A红外探测器,根据其技术手册,将仿真时的探测器的盲元率设置为0.3 %,并假设死像元和过热像元各占一半。死像元灰度值为0,过热像元的灰度值为255。红外系统的噪声来源多种多样,有光子噪声,暗电流噪声,热噪声,1/f噪声等等。进行噪声模拟时采用高斯随机噪声就可以得到比较好的效果[13]。仿真中探测器像元的噪声体现在非均匀性,本文将红外系统的输出电路和显示器上的噪声综合考虑为成像噪声,服从均值为5,方差为2的高斯分布。
5 仿真结果与分析
本文仿真的目标包括圆锥,球底锥和圆柱弧形碎片,仿真的目标形状和运动参数见表1。仿真时假设目标运动的起点地理坐标为(120°E,55°N),终点为(70°E,45°N),距离大气层的高度均为150 km,探测器在(95°E,45°N)处离地面300 km的位置以6.2 km/s的速度进行跟踪。整个过程目标飞行时间为699.59 s,在363 s时目标和探测器距离在10 m之内。运动轨迹可参见图7。
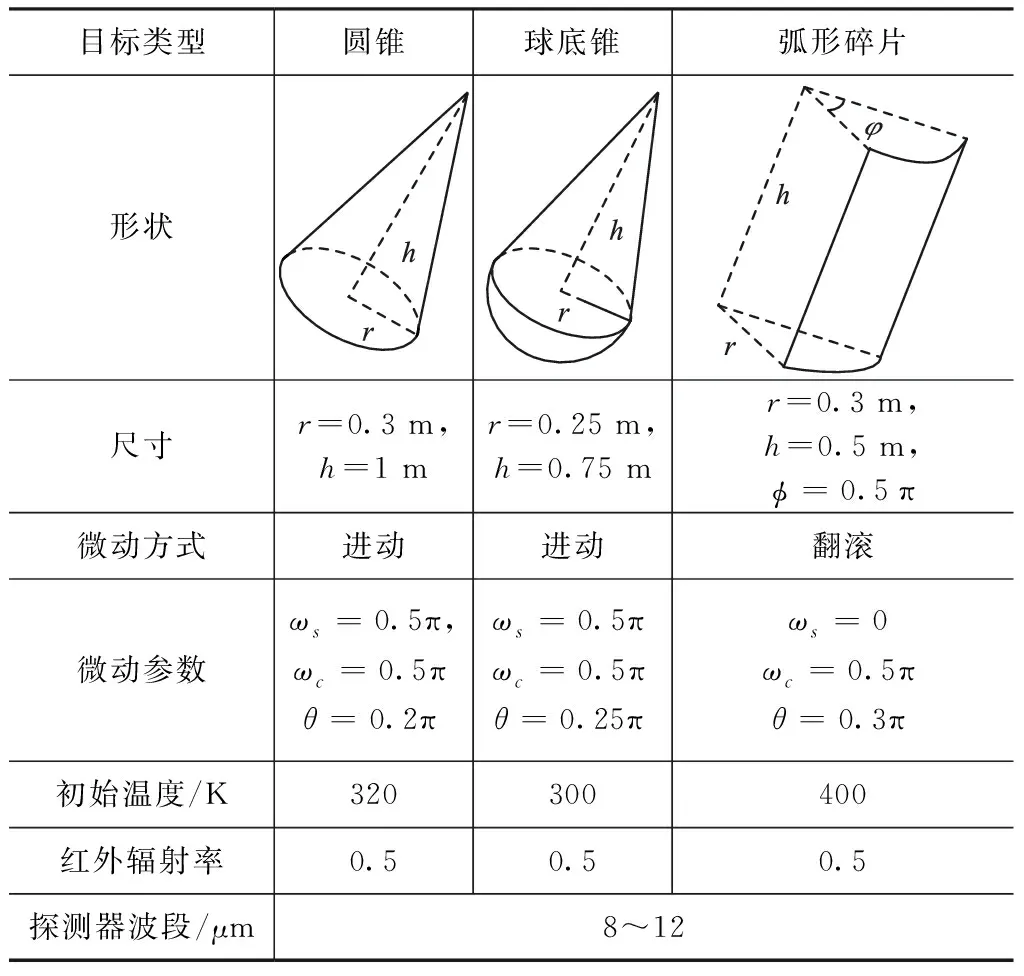
表1 目标红外辐射序列仿真参数Tab.1 Target infrared radiation sequencesimulation parameters
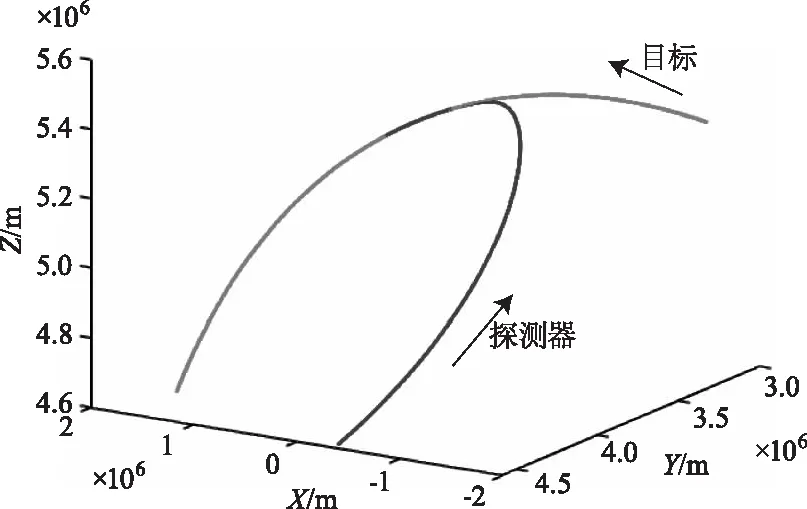
图7 目标和探测器仿真轨迹Fig.7 Target and detector simulation trajectory
其中,为了满足在百公里外实现目标识别的要求,选取了探测器在180~200 s运动时接收的红外辐射,此时二者的距离可达到150 km以上。仿真时每次观测单个目标,不考虑一次观测多个目标的情况。进行灰度量化时,公式利用在20 s观测时长内探测器接受的最大和最小辐射强度来生成灰度序列。

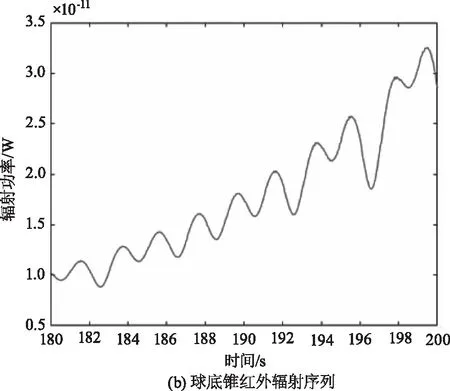
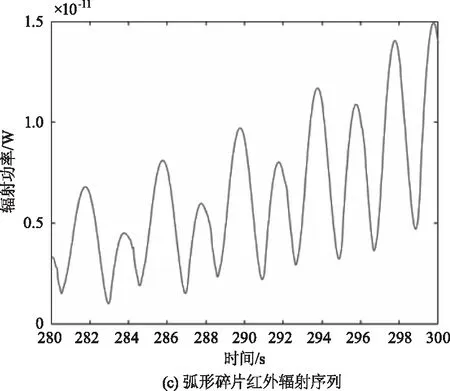
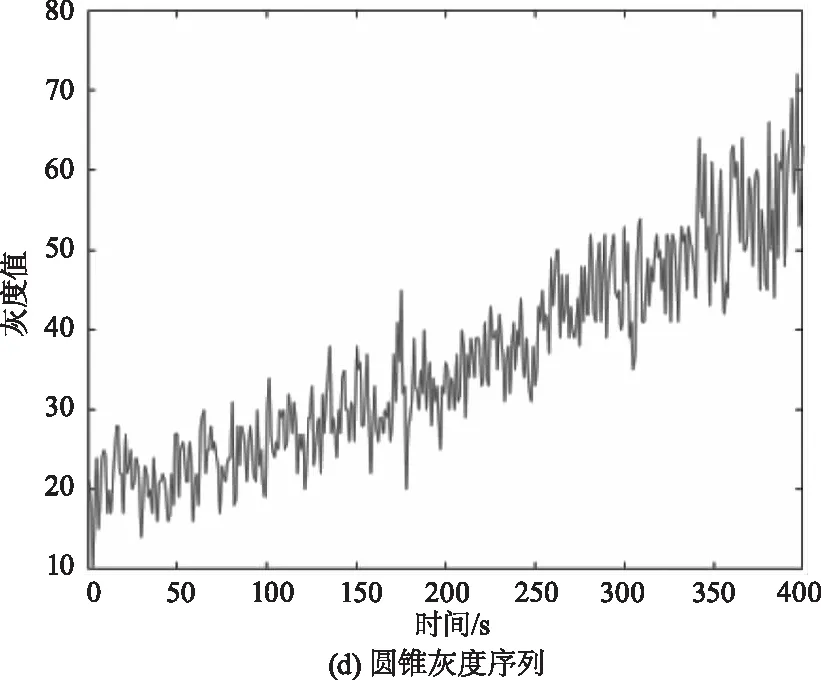
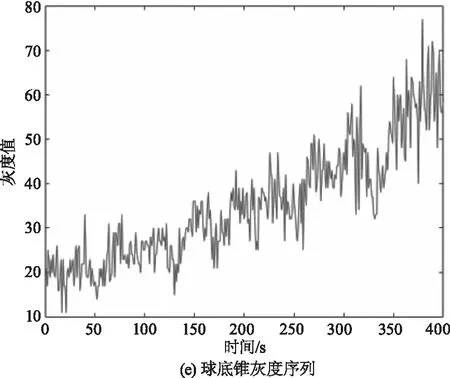
按照表格1仿真得到的不同目标的红外辐射强度序列见图8的(a)~(c),由于自旋和锥旋运动是匀速的,接收的红外辐射强度总体上有周期性,且不同目标的辐射强度大小也有明显的区别。随着探测器和目标之间距离的减小,红外辐射也在逐渐上升。仿真的目标红外辐射强度序列是理想化的情况,(d)~(e)的红外灰度仿真综合了探测器的成像效应后,序列中增加了噪声影响,序列变得杂乱,提高了识别难度,同时灰度序列的范围均在[0~80]范围,识别算法难以直接利用数值大小,更接近于实际情况。
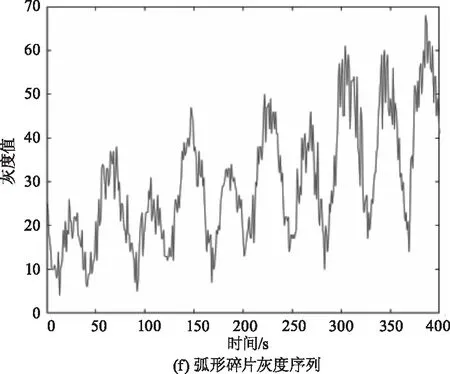
图8 红外辐射仿真和灰度仿真结果Fig.8 Infrared radiation and grayscale simulation results
6 结 语
本文建立了空间目标和探测器的运动模型,利用微动力学分析不同类型目标微动特征得到了探测器的观测的投影面积变化,并综合目标表面的温度变化,分析得到了目标红外辐射强度动态序列模型。并在仿真中引入了红外探测器的自身成像效应的影响,利用点扩散函数模拟焦平面弥散,加入像元非均匀性和盲元及噪声的影响,计算得到红外灰度序列信息。本文的红外序列仿真结果更接近真实观测情况,可以为红外目标识别算法提供数据支持。后续可利用仿真数据进一步开展识别算法的研究。
