基于侧信道与量化推理缺陷的模型逆向攻击

2021-09-08李景海唐明黄诚轩

网络与信息安全学报 2021年4期

关键词：攻击者功耗逆向

李景海，唐明,2，黄诚轩

基于侧信道与量化推理缺陷的模型逆向攻击

李景海1，唐明1,2，黄诚轩1

（1. 武汉大学国家网络安全学院空天信息安全与可信计算教育部重点实验室，湖北武汉 430072；2. 密码科学技术国家重点实验室，北京 100878）

AI安全；模型逆向攻击；量化推理缺陷；侧信道分析；Cluster-basedSCA

1 引言

随着大数据时代的到来以及计算机计算速度的显著提升，人工智能迎来快速发展，广泛应用于图像识别、语音识别、自然语言处理等任务。深度学习是应用最为广泛的人工智能技术之一。深度学习以深度神经网络（DNN，deep neural network）模型为核心，以数据为驱动，通过训练出具有良好表达能力的DNN模型对问题进行建模并解决。深度学习在人类社会各个领域都发挥了巨大作用，但同样存在巨大的安全风险。现阶段深度学习的安全研究集中于边缘端的模型推理过程，包括对抗样本[1-2]、数据投毒[3-4]、成员推断[5]、模型逆向[6-8]等方面。本文以模型逆向攻击为研究对象，模型逆向攻击是指攻击者通过各种方式提取出DNN模型的有关信息，包括模型的结构、模型的权重。模型结构与权重构成了整个神经网络，一旦攻击者通过模型逆向攻击恢复了网络模型的结构与权重，模型的推理过程就完全暴露在攻击者的视野中，攻击者可在短时间内完成如对抗样本等高阶攻击，对深度学习系统造成巨大危害。

传统的模型逆向攻击使用Query-based方法[6-7,9]，通过向模型输入数据并获得输出从而构造影子数据集，将影子数据集作为训练数据集训练一个替代模型来拟合原始模型进行模型的逆向。近两年，针对模型逆向攻击，出现了基于侧信道的新形式的攻击方法[8,10-12]。基于侧信道的攻击以DNN的具体实现为攻击点，通过分析计算设备在运行DNN时产生的侧信道信息（如功耗等）来提取模型结构和权重等隐私信息。本文以AI芯片来指代实现模型推理的实际计算设备。侧信道攻击主要用于密码学中各加密算法的密钥恢复中，对称加密算法和神经网络算法在结构与计算过程上具有相似性，在算法结构上，对称密码算法由轮函数串联而成，DNN则由多层网络层组成，二者都存在线性部件和非线性部件；在运行模式上，二者后一层/轮的输入取决于前一层/轮的输出，存在显式的中间值结果。基于这种相似性，侧信道攻击开始用于DNN的模型逆向攻击。

Hua等[10]通过测量模型运行过程中产生的内存访问模式信息，成功地逆向了基于FPGA实现的CNN模型的结构。Hu等[12]将视线转移到通用的GPU平台，测量了在GPU上运行产生的kernel events和对应的内存访问模式，将结构逆向问题转化为一个序列识别的问题，采用ASR中常用的LSTM+CTC的解决方案逆向了基于GPU实现的DNN 结构。Batina等[8]通过测量模型运行过程中产生的电磁信号，成功逆向了ARM Cortex-M3平台上实现的DNN的层数、每层神经元数量、激活函数类别等信息。Wei等[11]则通过测量功耗逆向了CNN的输入。在已有研究中，以内存状态为数据来源的方法存在数据采集困难的问题。内存状态信息的获取要求攻击者对AI芯片有较高的访问权限或者通过硬件木马来收集内存信息，这对于攻击者而言是很高的能力要求。而基于物理侧信道的方法存在如下问题：其使用CPA技术来逆向模型权重，这种方法要求攻击者构造足够准确的泄露模型完成假设中间值到侧信道信息的映射，这需要攻击者掌握设备的底层硬件电路设计，而AI芯片的设计细节是生产商的重要知识产权，出于对知识产权的保护，加速卡生产商不会公布加速卡的内部细节，因此攻击者无法有效构造准确的泄露模型。为了解决这一问题，本文提出了一种新的攻击方法，该方法无须攻击者构造泄露模型。

本文方法的出发点来自当AI芯片使用了量化推理技术后，模型逆向攻击变得更有可能实现。量化推理[13-15]是AI芯片为了减小模型存储开销和加速模型的推理广泛使用的技术。量化推理中，FP32的模型权重与激活值使用更低精度的FP16或INT8类型表示，来减小存储开销与提高计算速度，AI芯片会设计专门的部件来适配低精度情况下的模型推理，如 Xilinx的DPU、Google的TPU[16]等。量化推理存在潜在的安全威胁，因为量化技术使表示单个权重所需要的比特数大大降低，攻击者可以更加容易地枚举所有可能权重并验证是否正确，从而恢复出正确的权重；另外，量化推理导致了一种输出序列分类不等价的现象，这启发笔者使用猜测权重的平均离散系数为指标来判断猜测权重正确与否，这种方法被称为cluster-based side-channel analysis，简称cluster-based SCA。

本文的主要工作如下。

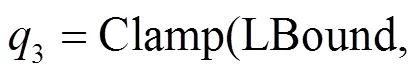
（2）提出了新的基于侧信道的攻击方法 Cluster-based SCA，该方法不需要攻击者构造特定的泄露模型。利用Cluster-based SCA构造了模型权重逆向的攻击，并进行了仿真实验来验证方法的有效性。

（3）分析了 Cluster-based SCA 方法的性质。

2 背景知识

2.1 侧信道分析

侧信道分析（SCA，side-channel analysis）利用算法在运行时产生的侧信道信息，如功耗、时间等来推测算法的私密信息。侧信道分析的研究起源于密码学[17]，通过分析加密设备在加密过程产生的侧信道信息来推测密钥，包括SPA（simple power analysis）[18]、DPA（differential power analysis）[19]、CPA（correlation power analysis）[20]等技术，相比基于统计分析的密钥恢复攻击，SCA的优势在于其采取了分而治之的思想，通过逐个恢复密钥中的较小部分，通常为单个字节，从而减少了密钥恢复的复杂度。侧信道攻击中的几种基本方法如下。

SPA：简单能量分析是SCA的基本形式，SPA是从密码芯片运算的功耗波形上能够直接找出密钥信息的攻击方法。在芯片中，密钥位为0时运算的功耗和密钥位为1时运算的功耗存在差异，通过这样的差异分析出密钥位的值，按照一定规律组合得到完整的密钥。SPA常用于攻击RSA算法，通过区分平方运算和乘法运算，逐步恢复出密钥。

DPA：差分能量分析是SCA的高级形式，它是以能量消耗曲线为基础，再以统计方式推演密钥的攻击技术。在攻击中，攻击者首先对密钥进行假设，并据此计算出中间值。根据中间值取值将采集到的功耗曲线分为两个或多个集合，并计算这些集合的均值的差来验证假设是否正确从而恢复出密钥。

CPA：相关能量分析是DPA的一种变体，其使用Pearson相关系数作为统计指标进行猜测正确与否的确认。文献[8]中使用CPA进行神经网络模型参数的恢复。CPA恢复密钥的主要步骤如下。

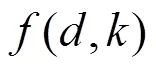
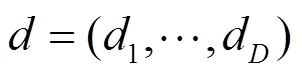
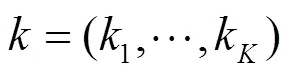
2.2 DNN中的原子操作

本文使用DNN表示仅有全连接层的网络以及带有卷积层的CNN。DNN由多种类型网络层串联而成，本文不考虑Resnet中的shortcut和GoogLeNet中的Inception模块。常见的网络层类型有卷积层、池化层、全连接层、BN层等。其中最主要的两种类型为卷积层和全连接层，Krizhevsky在文献[21]中提出了两点观察结论：卷积层占据了90%～95% 的计算时间和5%权重数量，且有较大的值；全连接层占据了5%～10% 的计算时间和95%的权重数量，且值较小。这两层的运算都可以转换为通用矩阵乘法运算。卷积层内每个神经元都与前一层中位置接近的区域的多个神经元相连，区域的大小取决于卷积核的大小，被称为“感受野”。卷积核在工作时，在“感受野”内对输入特征做矩阵元素乘法求和并叠加偏差量，送入激活函数后生成特征图作为下一层的输入。图1展示了如何将卷积层的计算转换为通用矩阵乘法计算。

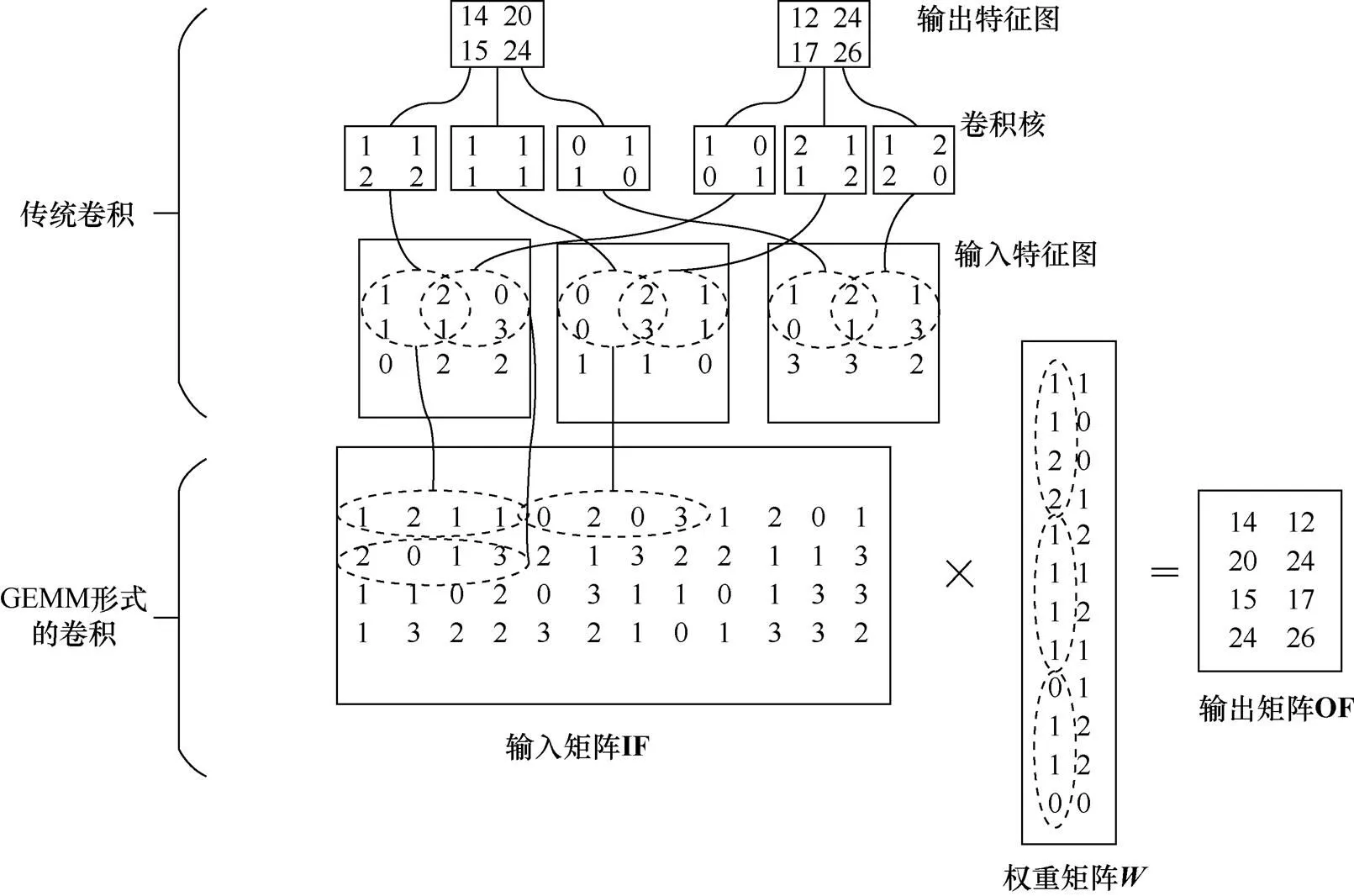
图1 卷积计算与GEMM之间的转换

Figure 1 Transformation between convolution operation and GEMM

如图1所示，对于输入特征图为 3×3×3，卷积核为2×2×3×2 的情况，通过将每一通道在单次卷积操作中涉及的操作数按行展开并将卷积核对应的元素按列展开，即可将原始的卷积操作展开成矩阵乘法。原始卷积操作等价于式(1)。

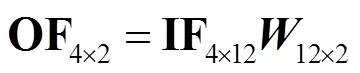
其中，IF为输入特征矩阵，为权重矩阵，OF为输出特征矩阵。原始的卷积核元素被转换为矩阵乘法的操作数。

全连接层可以看成卷积核尺寸与输入特征图相同的卷积层，其底层操作仍然可以转换为通用矩阵乘法。而通用矩阵乘法由标量乘法组成，对于卷积层或全连接层的输出值，其可以表示为式(2)。

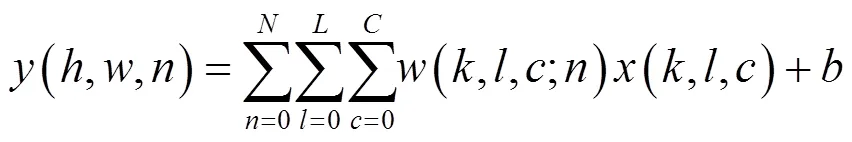
2.3 量化推理

量化完成从原始数据类型到量化后数据类型的转化，使用式(3)计算。

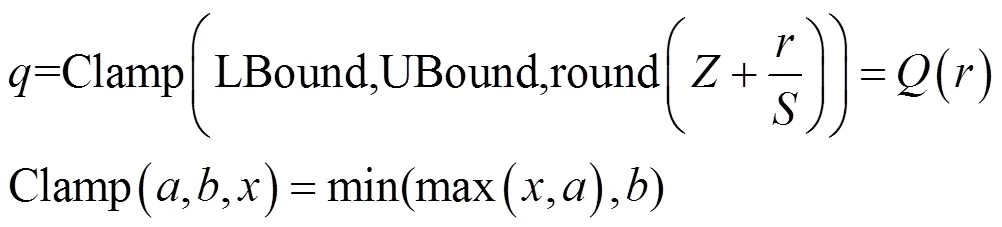
反量化完成量化后数据类型到原始数据类型的转化，使用式(4)计算。

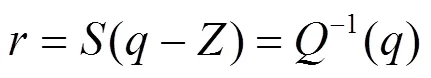
目前，已有大量的论文对量化推理进行了研究，根据量化后的数据类型可以分为FP16 量化、INT8 量化[14]，以及更加激进的XNORNet[15]等，其量化精度高，模型准确率损失小，但量化效果差，而过低精度的量化在显著提升量化效果时带来了更大的模型准确度损失。通过权衡，现阶段最成熟的量化方案为INT8量化，如Google 的Tensorlite、Nvidia的TensorRT、腾讯的NCNN。

Google 发布的白皮书[23]对现有的INT8 量化方案做了全面的介绍，其将量化方案分为Uniform Affine Quantizer、Uniform Symmetric Quantizer 和Stochastic Quantizer。本文第3节以Uniform Symmetric Quantizer 为例，分析量化操作中存在的安全风险，这是Cluster-based SCA方法的理论基础。

2.4 AI芯片

本文以AI 芯片来指代实现模型推理的实际计算设备。AI 芯片是逆向目标DNN 模型的运行载体，其在执行模型计算任务时产生意外的侧信道信息泄露，从而泄露与模型有关的隐私信息。AI芯片采用专卡专用的模式，使用特定架构专注于模型计算任务。专卡专用的模式减少了加速卡内部与模型计算无关的任务的执行，提高了运行时产生的侧信道信息与神经网络模型的相关性，这种更为纯净的侧信道信息提升了攻击者从采集到的侧信道信息中恢复模型结构权重的可能性。AI芯片根据技术路线可分为GPU、FPGA、ASIC。AI芯片的架构与底层实现一般不会公开，尤其是ASIC实现的AI芯片，其对于用户为完全的黑盒状态。AI芯片以加速模型推理为目的，而量化推理作为一种常见的算法层的模型优化与推理加速方案，具有实现简单、效果明显的优点。因此，AI芯片在底层架构中针对量化推理进行了适配，加入了定制的低精度运算部件。目前，全球芯片企业都在积极地进行AI芯片的布局。Google、Nvidia、Xilinx等企业发布了自己的AI芯片产品。表1列举了现阶段部分AI 芯片产品及其对量化推理的支持。

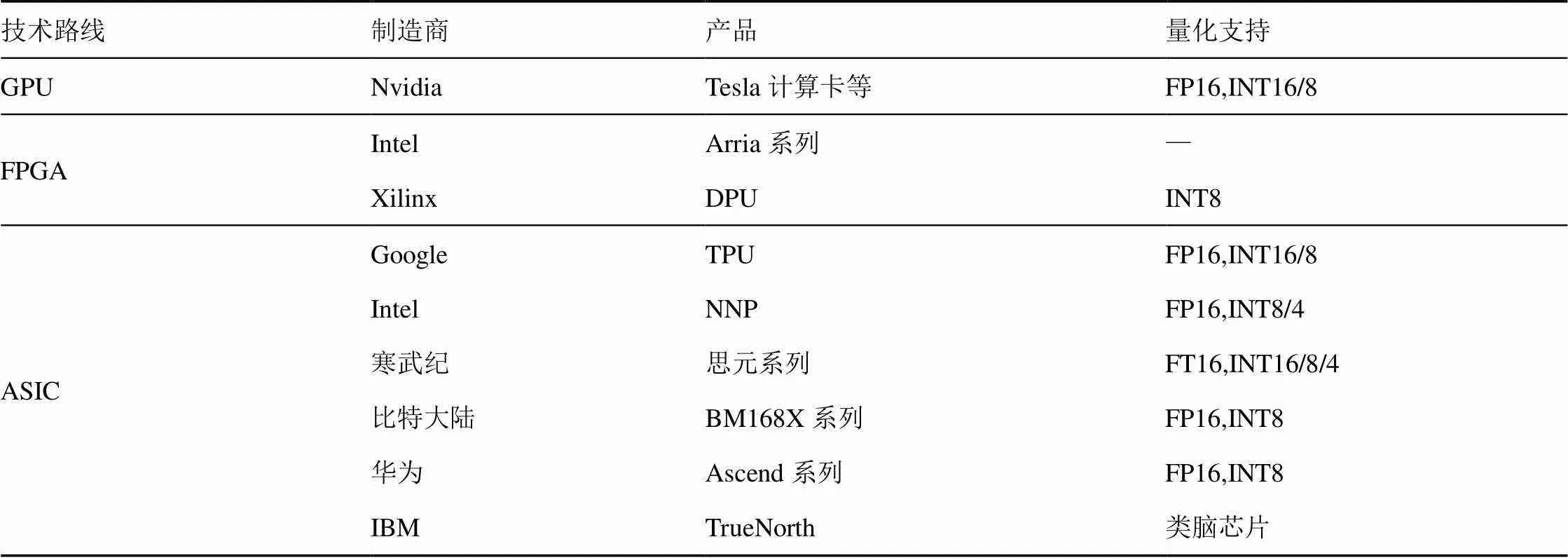
表1 主流AI芯片对比

3 量化推理中的安全风险

量化推理虽然带来了更快的推理速度和更低的运行功耗，但同时带来了安全风险。由于低精度数据的表达能力有限，其在运算过程中会损失许多有用的数据。本节以Uniform Symmetric Quantizer[23]下的INT8 量化为例说明量化推理中存在的安全风险，对于其他量化策略，该风险依然存在。

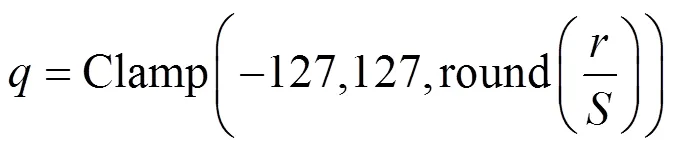
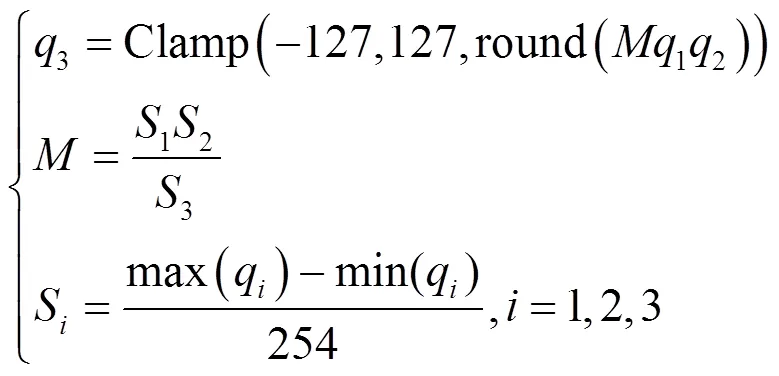
3.1 分类不等价

这里首先给出分类不等价的概念，方便后续说明。

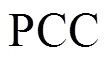
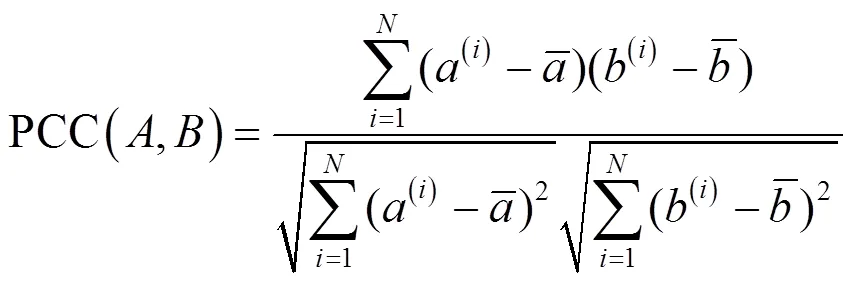
3.2 量化乘法中的分类不等价

3.3 量化乘法分类不等价的来源

本节讨论量化乘法中分类不等价现象产生原因。量化推理操作导致的这种输出序列分类不等价现象来源可以分为两部分。第一部分来源于量化操作中round的函数；第二部分来源于量化操作中Clamp的函数。

由于量化推理DNN中的绝大部分计算为量化乘法，基于量化乘法操作导致的这种输出序列分类不等价性，本文结合侧信道分析构造了一种新型的攻击方式来逆向DNN中的权重。

4 攻击方法

4.1 攻击场景与攻击者能力假设

本节考虑这种场景下的攻击：攻击者伪装成使用终端推理服务的普通用户，其可获取AI 芯片，使用量化推理技术来加速模型推理过程，上部署了DNN 模型，攻击者可以获取运行DNN 模型产生的功耗，攻击者的目标为使用模型逆向方法恢复DNN 模型权重集合。其中，权重集合包含神经网络中全连接层和卷积层的所有权重值。这样的场景广泛存在于安防摄像头、无人驾驶、智能家居设备、AIoT 等边缘计算环境。例如，在图3无人驾驶汽车场景，广泛使用AI芯片加速目标识别等任务。

对于攻击者，做出如下攻击者能力假设。

① 在信息收集阶段，可获得部署了攻击目标模型的AI芯片，控制模型的输入，获得其输出，并且可以测量加速卡运行DNN模型时产生的功耗。

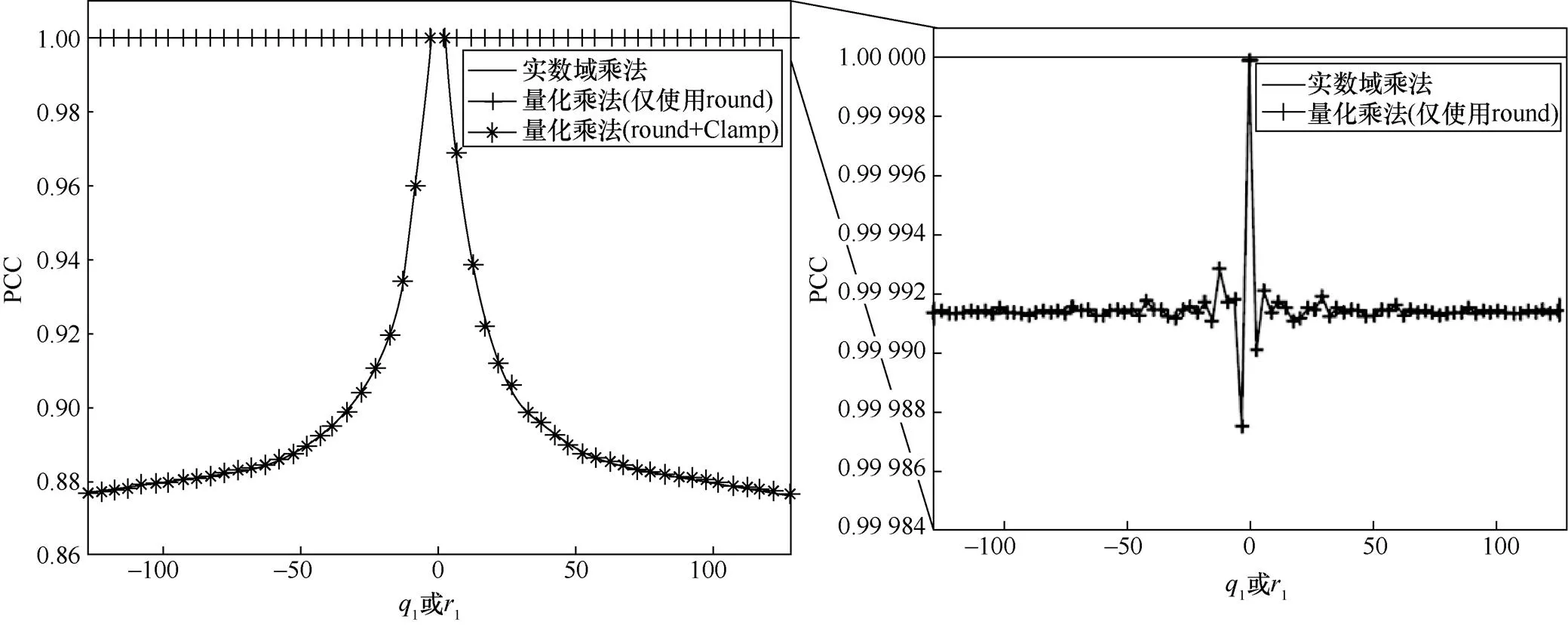
图2 FP32乘法、量化乘法（仅使用round函数）、量化乘法（round+Clamp）在输出序列分类不等价性上的区别

Figure 2 The difference of classification unequivalence between FP32 multiplication, quantized multiplication(only round),quantized multiplication(round+Clamp)

② 攻击者获取了模型各层的量化参数和模型的结构。

③ 攻击者不了解AI 芯片内部的架构设计细节，也无法得知AI 芯片对网络层的底层实现，AI 芯片对于攻击者来说是一个完全的黑盒。

在攻击者能力假设中，对于假设①，攻击者可以直接通过购买等方式获得部署了攻击目标模型的AI芯片并使用各种示波器和探头获取芯片运行时产生的功耗。对于假设②中的模型结构信息，在实际环境中也可以满足，现今神经网络的发展类似于加密算法的发展，模型大多公开或者直接使用开源模型，而对数据集进行保密。另外，攻击者可以使用模型逆向的方法来恢复模型结构[8,12]。在攻击者能力假设下，攻击者无法获得关于AI 芯片的内部实现细节，无法构造有效的泄露模型。因此，本文使用Cluster-based SCA来进行权重的逆向。

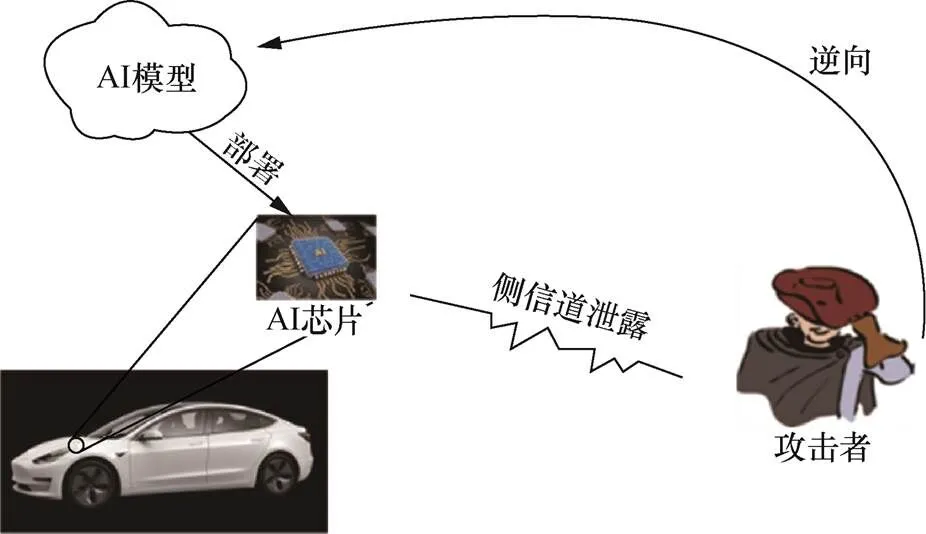
图3 攻击场景：无人驾驶

Figure 3 Attack scenario: automatic drive

4.2 Cluster-based SCA方法

本节介绍Cluster-based SCA方法的原理。Cluster-based SCA方法的优点在于其不需要攻击者构造泄露模型。本文使用Uniform Symmetric Quantizer量化方案的乘法（表示为式(5)）。

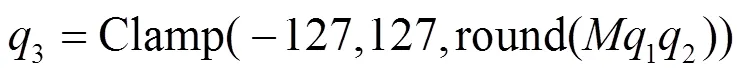
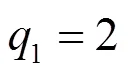
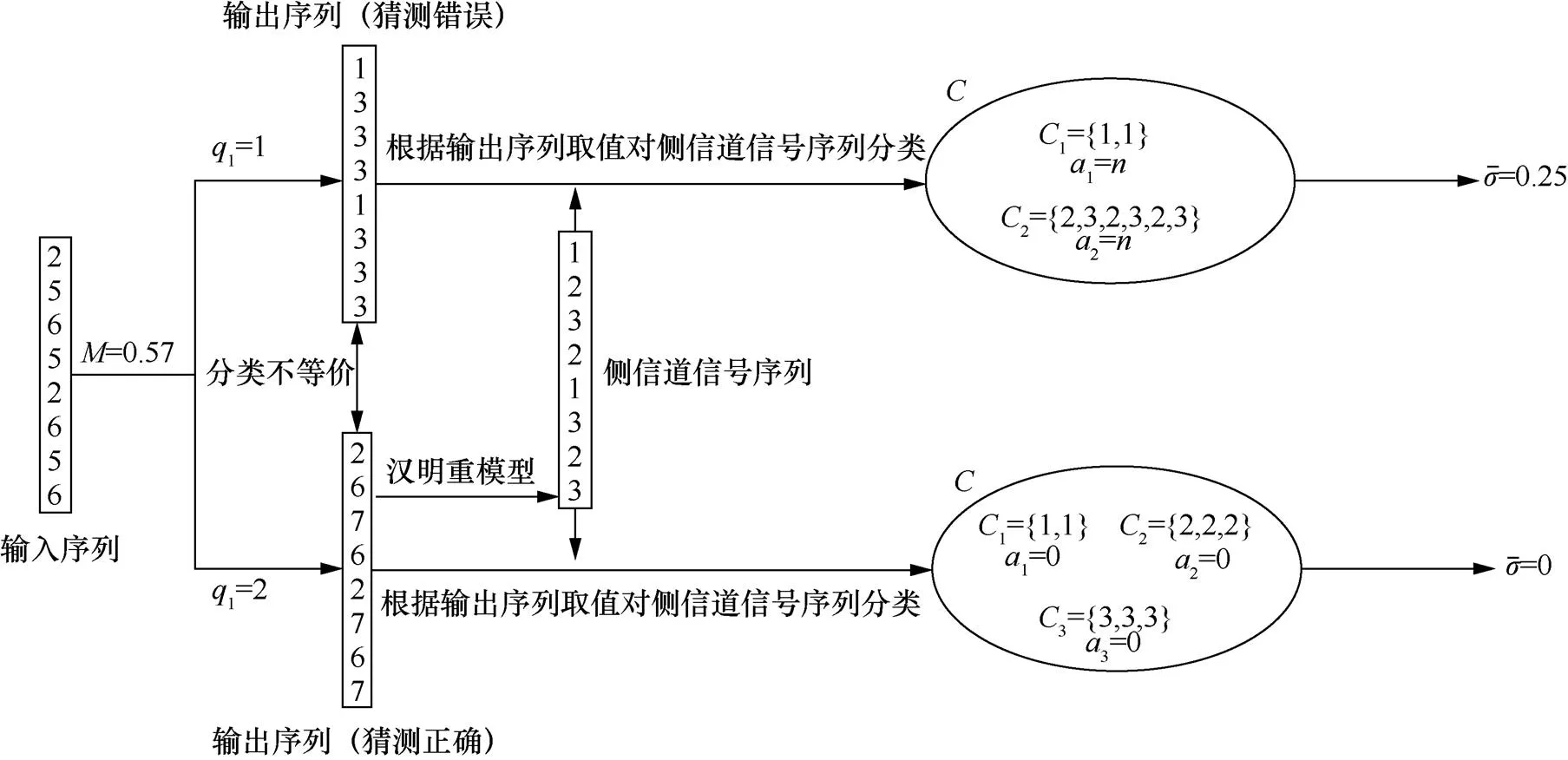
图4 Cluster-based SCA方法实例（M=0.57）

Figure 4 An instance of Cluster-based SCA (=0.57)

算法1 Cluster-based SCA

end

=ClusterWithKey(KV)

for=1:|| do

end

4.3 Cluster-based SCA方法分析

4.3.1 对称性

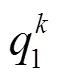
4.3.2 不均匀性

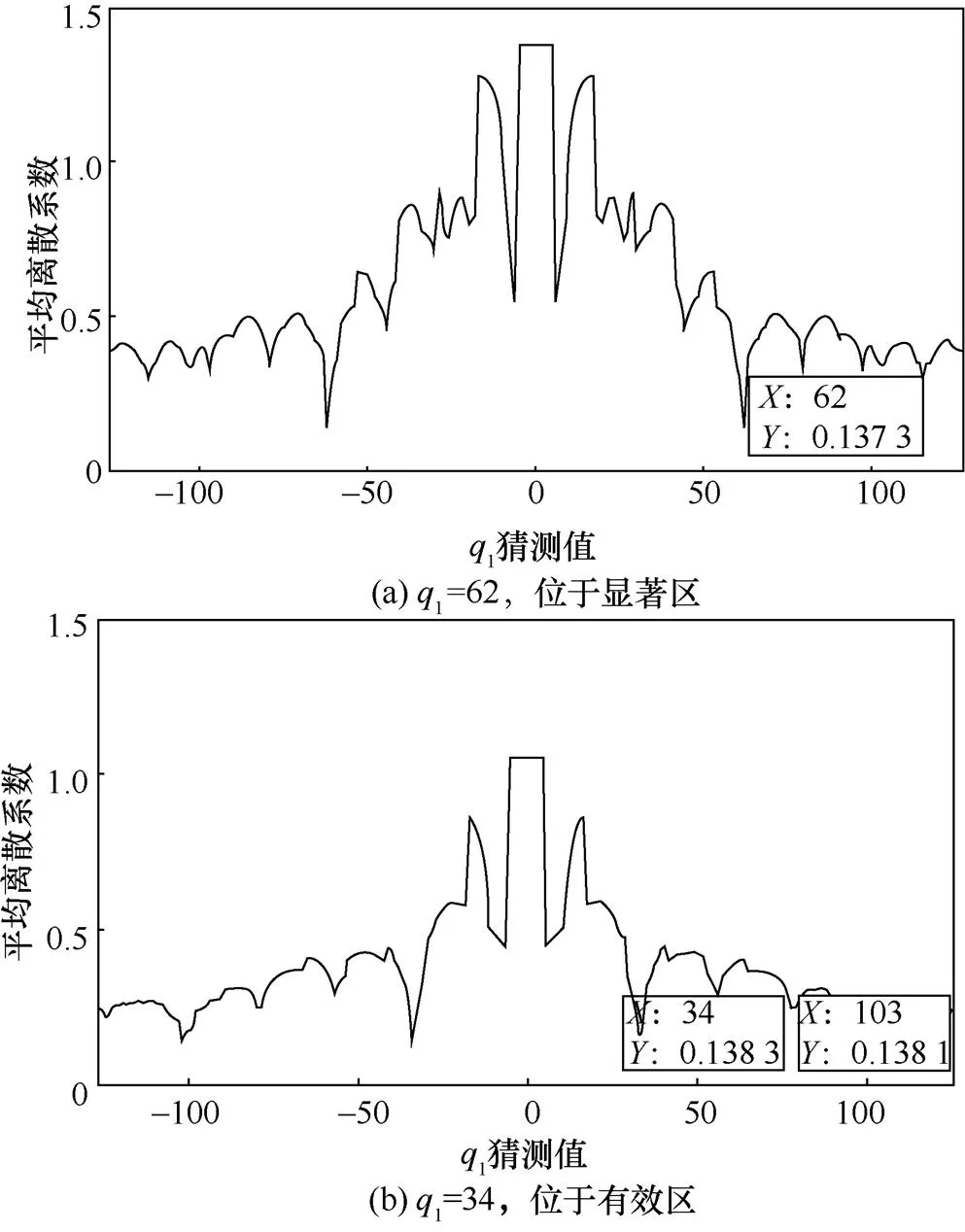
图5 不同取值Cluster-based SCA的恢复效果

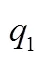
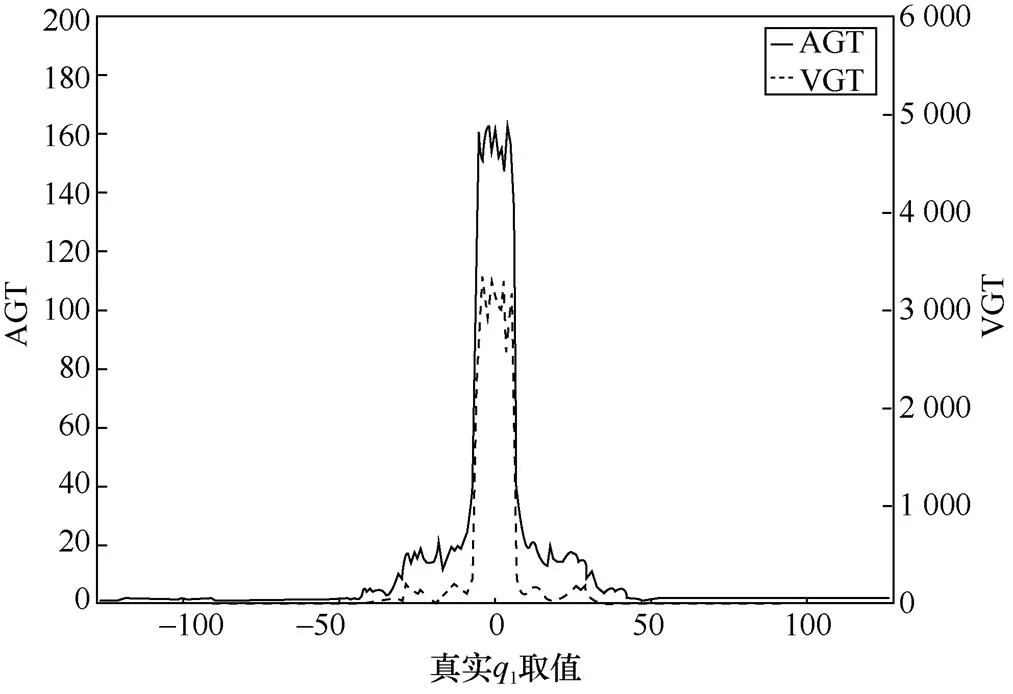
图6 Cluster-based SCA的不均匀性（M=0.000 663）

Figure6 Nonuniformity of Cluster-based SCA (=0.000 663)

4.4 基于Cluster-based SCA的模型权重逆向

本节使用Cluster-based方法来逆向模型的权重。本节将全连接层视为卷积核尺寸等于输入特征图尺寸的特殊卷积层，根据2.1节和2.2 节的分析，在量化推理中，FP32类型权重值与特征值均被转换为INT8类型的数据，全连接层和卷积层的输出在进入激活函数之前，可以统一表示为式(7)。

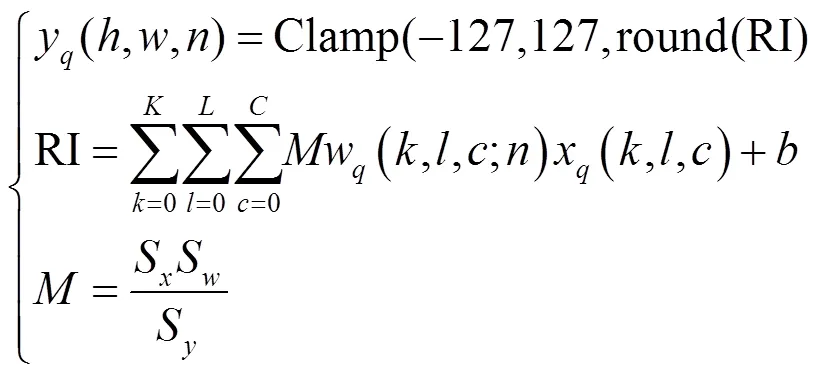
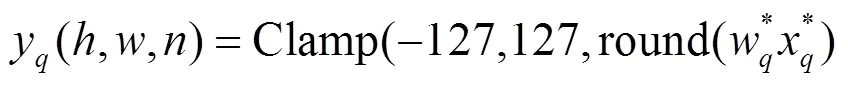
5 仿真实验

5.1 实验设置

为探究不同网络结构对方法的影响，本文实验部分采取了10种不同结构的网络，其拥有不同的卷积层设置，详细设置如表2所示。

为探究曲线条数对方法的影响，实验对于每一种网络结构，设置了10种曲线条数取值情况，从1 000到10 000。为探究噪声对方法的影响，实验对于每一种网络结构，曲线条数取5 000时，设置了10种噪声方差取值情况，从0.1到1.0。

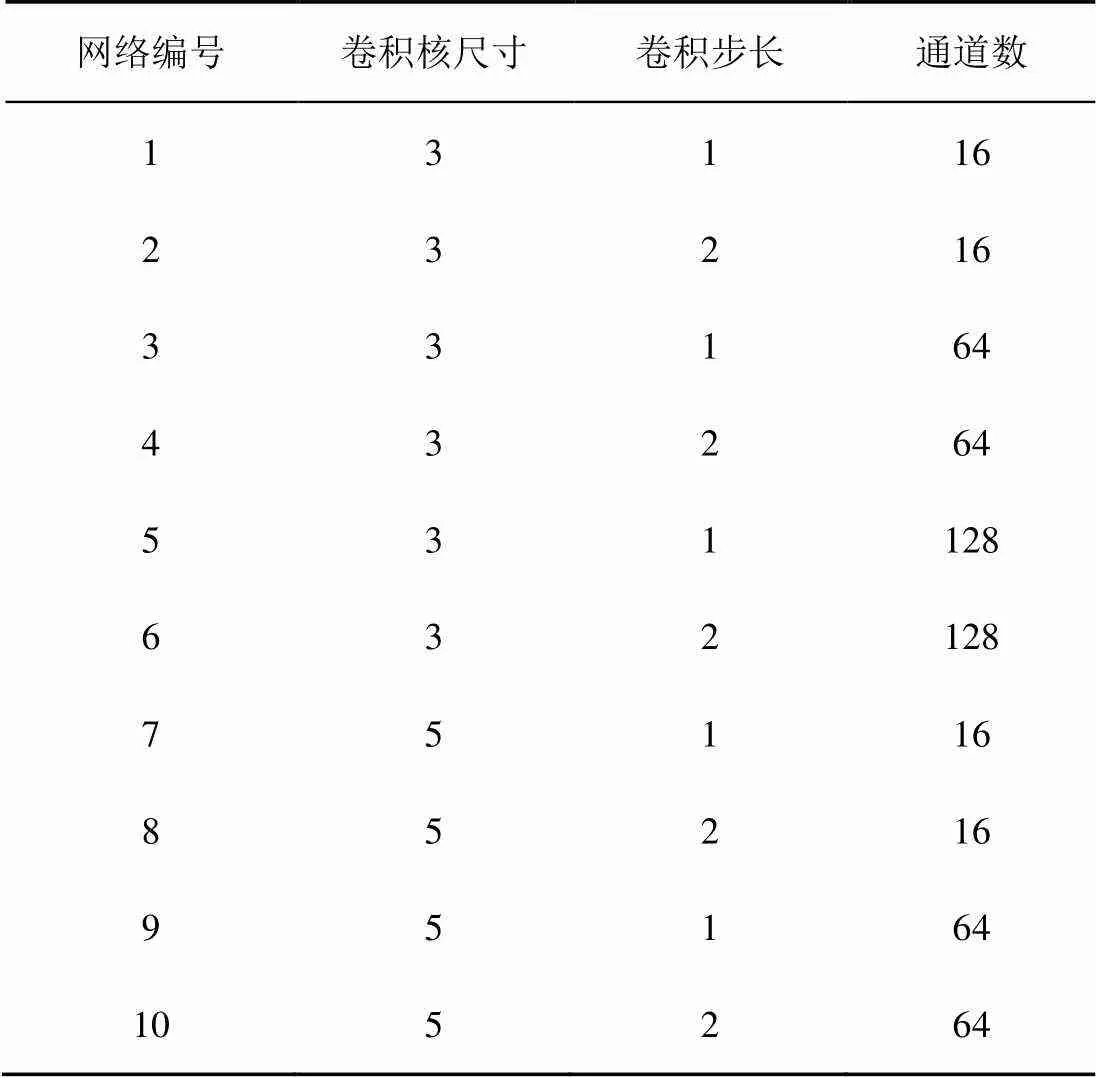
表2 实验网络层结构

实验使用Cluster-based SCA方法分别恢复了这10种网络结构的卷积层参数。

为了探究泄露模型对方法的影响，实验选取了5种不同的泄露模型进行对比，分别为汉明重模型与4种随机数模型（random leakage model）。使用汉明重模型为基准泄露模型来仿真AI芯片实际运行量化乘法时产生的功耗，并使用随机数模型进行对比实验。汉明重模型使用操作数的汉明重量作为其功耗，即INT8 数据二进制表示中置1的位数；随机数模型将操作数映射到一个随机功耗值。二者计算式见式(9)。本文引入了高斯噪声来模型实际情况下的环境噪声。值得注意的是，虽然使用了泄露模型，但在实际的Cluster-based SCA方法中并没有使用到任何与泄露模型有关的信息，其作用仅为得到仿真实验所需的仿真功耗值。

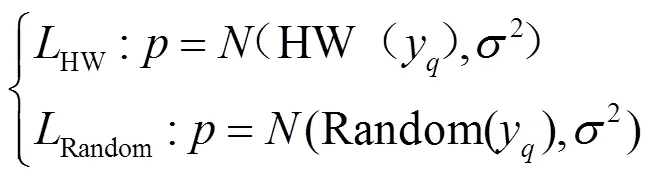
5.2 实验结果

实验使用Cluster-based SCA 方法恢复了所有实验目标CNN的第一层卷积层的所有权重，使用TOP恢复率来定量描述方法的效果。对于卷积核中的每一个权重，若其猜测序列前个猜测权重中包含正确值，则认为成功恢复该权重。TOP正确率等于卷积核中恢复成功的权重数量与总权重数量之比。

图7显示了共384次恢复实验的整体情况。

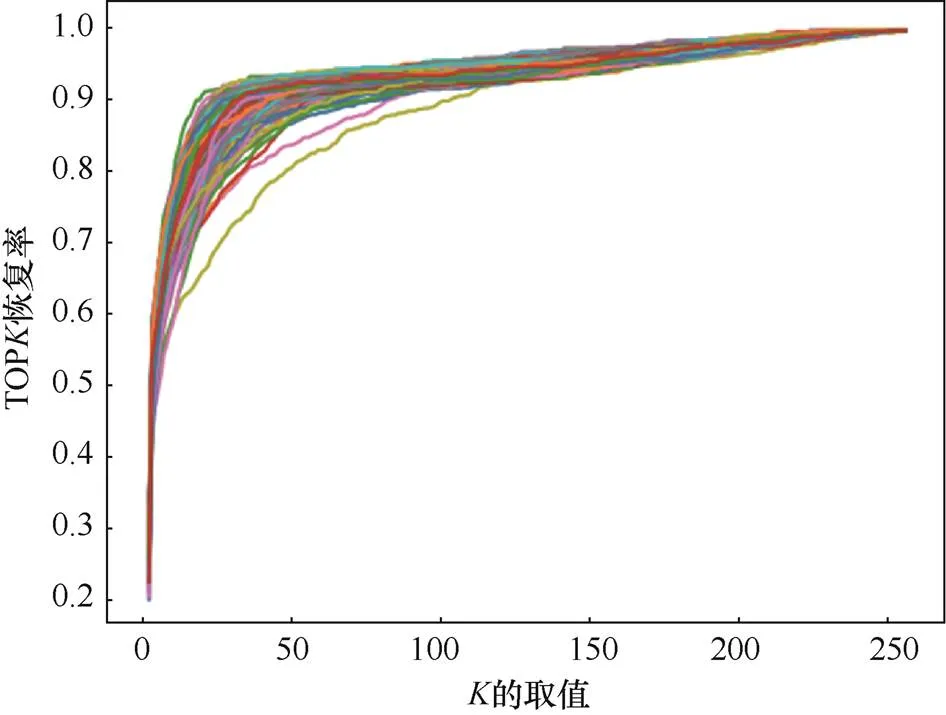
图7 恢复实验整体情况

Figure 7 The overall situation of the experiment

表3展示了不同网络结构、曲线条数以及取值情况下的正确率。曲线条数取值情况为100条、1 000条、2 000条、6 000条。TOP中取值情况为=1，=2，=5。从表3来看，曲线在各种结构下的TOP恢复率变化不大，这与理论分析相符合，即权重的恢复率取决于参数的分布情况，而与模型的结构无关。由于神经网络的训练特性，导致训练后的模型每一层的权重服从于高斯分布[24]。

图8 显示了Cluster-based SCA 方法TOP恢复率的实验结果。仿真泄露模型为汉明重模型，方差为0.2。由图8可以看出，Cluster-based SCA 方法在曲线条数为6 000时收敛到最佳效果。

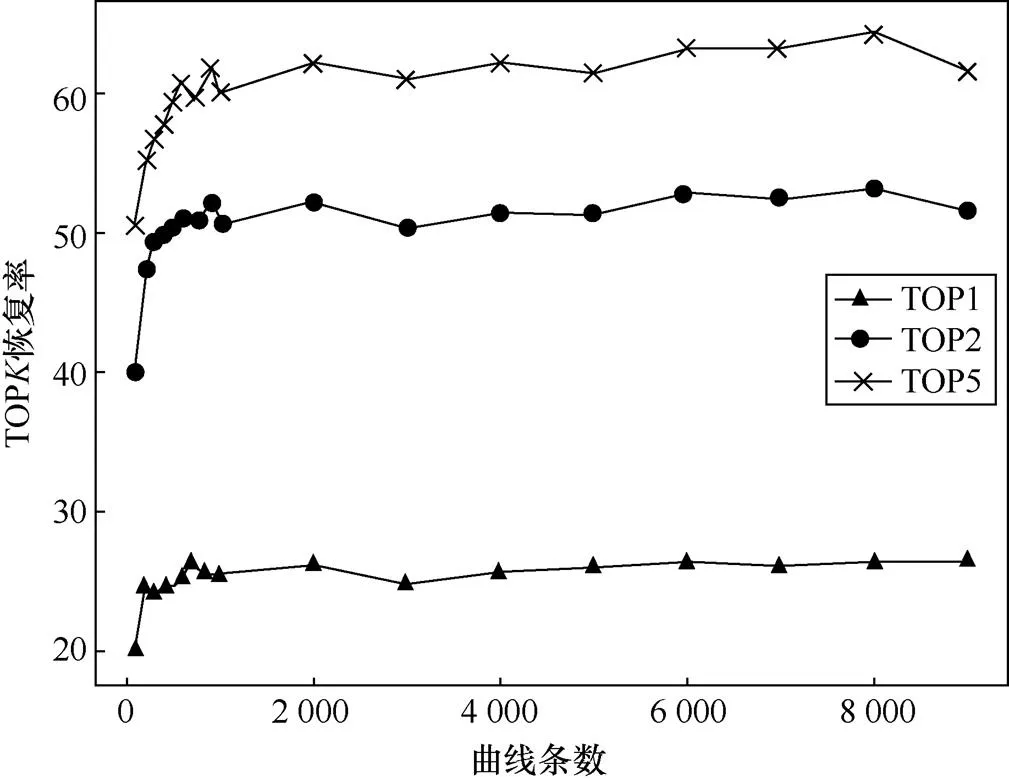
图8 TOPK恢复率随曲线条数的变化

Figure 8 TOPrecovery rate with respect to samples

图8中TOP2 正确率相对于TOP1 正确率提升了约100%。这是Cluster-based SCA 方法的对称性导致的。Cluster-based SCA对称性的存在，导致在恢复模型权重时只能恢复其绝对值。但这不是一个很大的问题，因为保持输入为正时，权重的正负将表现在输出值上，而根据文献[8]的研究，对于激活函数，其对于正负激活值的操作时间是存在巨大区别的，因此，攻击者可以使用激活函数的执行时间来分辨出权重值的正负。

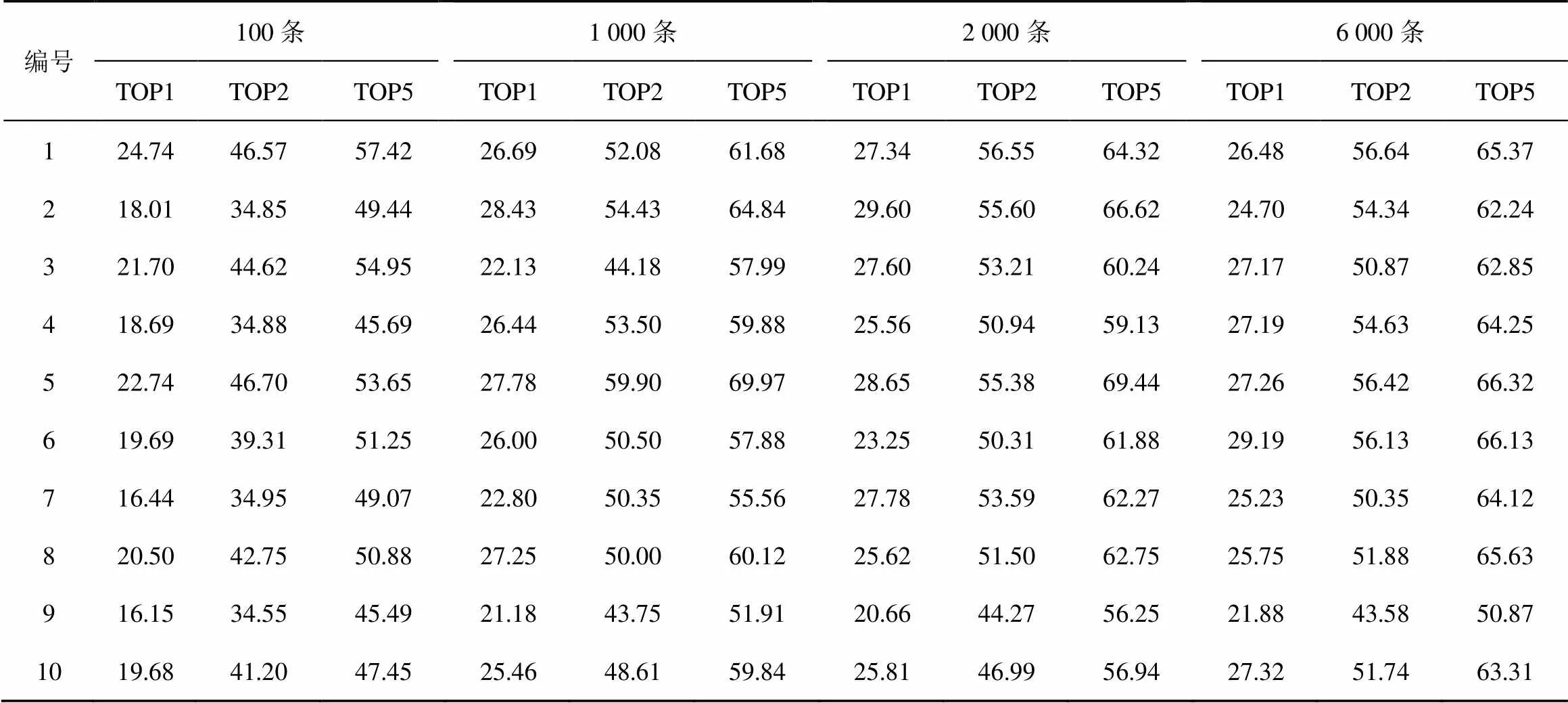
表3 不同网络结构、曲线条数以及K取值情况下的正确率

图9为曲线条数10 000 条，汉明重模型方差0.2时，TOP恢复率随值的变化曲线，图中TOP的恢复率在=1,2 时迅速增长，随后变缓，直到=243 才能达到100%。这是由于SCA 方法不均匀性导致的。具体地，模型权重TOP2恢复率为52.66%，此时成功恢复的权重包括位于显著区的权重（在=2时，其绝对值被恢复出来），以及部分位于有效区的权重。对于有效区的权重，由于不均匀性，最小的离散系数可能不由真实权重或其相反数产生，在这种情况下真实权重在猜测序列中的索引大于或等于2，具体索引值取决于噪声，带有随机性。但根据图5的结果，有效区的AGT指标和VGT指标仍相对较小，所以恢复率较快上升，对应图9中2<<40区间。而对于空洞区的权重，其真实权重在猜测序列中的索引完全随机，AGT指标和VGT指标高，所以恢复率上升变得缓慢，对应图9中≥40区间。

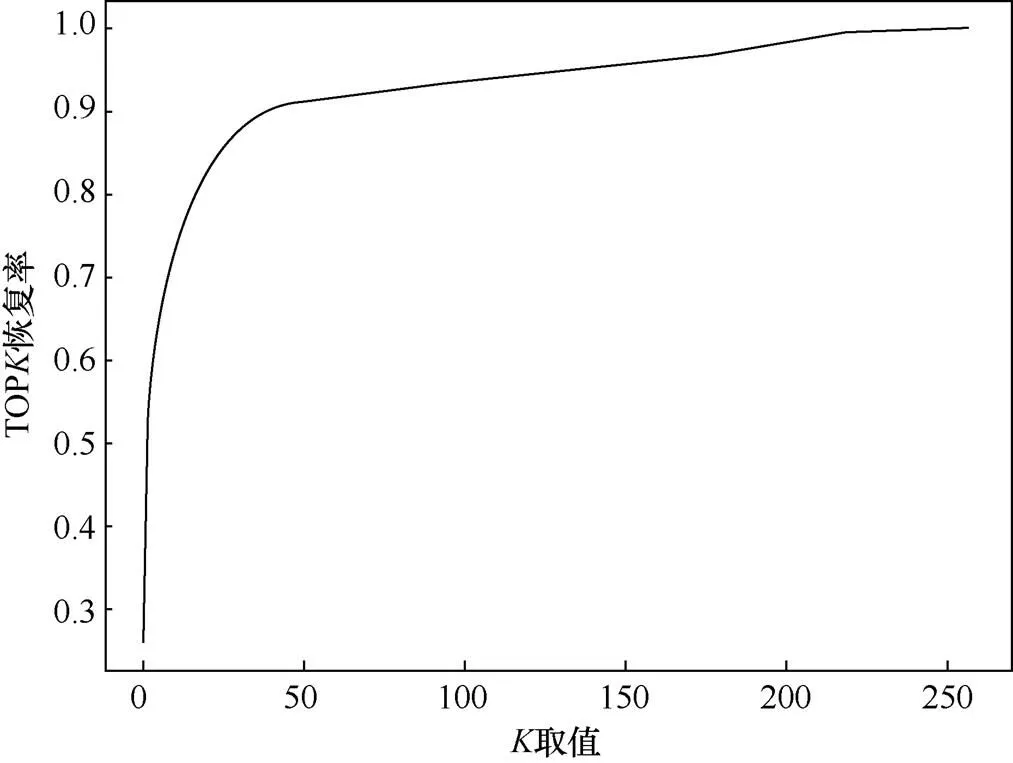
图9 TOPK恢复率随K值的变化

Figure 9 TOPrecovery rate with respect to

通过对基准泄露模型设定不同的方差值，本文分析了Cluster-based SCA 方法的抗噪声能力，共进行了11组实验，图10显示了Cluster-based SCA 方法在面对不同大小噪声时的表现，发现Cluster-based SCA 方法具有很强的抗噪声能力。

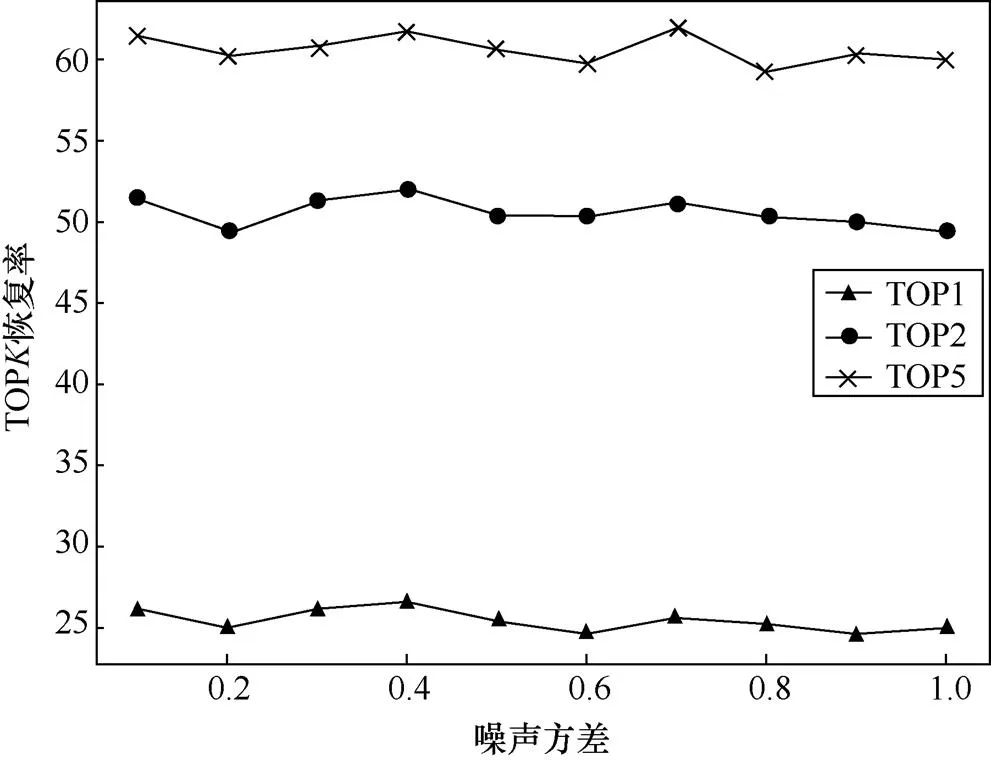
图10 TOPK恢复率随噪声的变化

Figure 10 TOPrecovery rate with respect to noise

最后选取4组随机数模型作为泄露模型，并与基准泄露模型的实验结果进行对比。图11的实验结果显示了本文方法对5组泄露模型的攻击呈现出稳定性。对于位于显著区的权重，Cluster-based SCA 均以接近100%的TOP2 恢复率完成了逆向。这验证了Cluster-based SCA 无须构造泄露模型信息的特点。

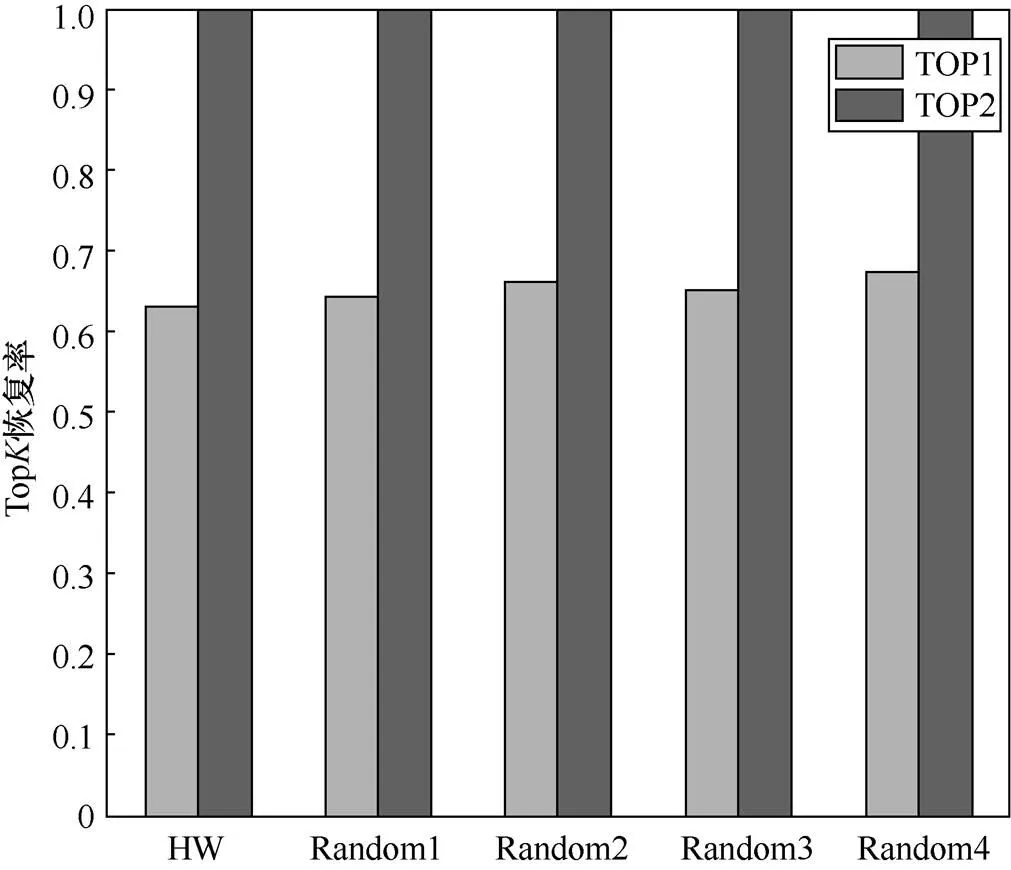
图11 TOPK恢复率随泄露模型的变化

Figure 11 TOPrecovery rate with respect to leakagemodel

6 结束语

本文以模型逆向攻击为研究目标，具体地，以部署在使用了量化推理技术的AI 芯片上的DNN 模型为攻击目标，旨在逆向DNN中卷积层和全连接层的权重。本文分析了量化推理过程，发现了其中存在的输出序列分类不等价现象，结合侧信道攻击，提出Cluster-based SCA 方法。现有的使用CPA方法恢复模型权重的方法，需要攻击者构造准确的泄露模型，要求攻击者十分了解AI芯片的底层实现，且具有丰富的经验，这是因为AI芯片本身具有的黑盒性而变得难以实现。而与CPA 方法相比，本文提出的Cluster-based SCA方法无须攻击者构建功耗模型，适用于未知实现细节的AI 芯片上的模型逆向，对于权重值较大的显著区，Cluster-based SCA 方法使攻击者权重恢复指标AGT 减少至1.5。本文进行了仿真实验，Cluster-based SCA 方法以52.66%的TOP2恢复率恢复了CNN第一层卷积层所有卷积核权重，对于取值位于显著区的权重，TOP2 的恢复率均达到了100%，并验证了方法的可行性，发现Cluster-based SCA 方法具有抗噪能力。

未来的工作将集中于：① 验证使用估计量化参数进行逆向的有效性以及提出应对措施解决Cluster-based SCA 的不均匀性问题；② 将Cluster-based SCA 方法用于实际的攻击环境中并对其进行评估；③ 给出针对Cluster-based SCA 的防护措施。

[1] KURAKIN A, GOODFELLOW I J, BENGIO S, et al. Adversarial examples in the physical world[J]. CoRR, abs/1607.02533, 2016.

[2] GOODFELLOW I J, SHLENS J, SZEGEDY C, et al. Explaining and harnessing adversarial examples[C]//3rd International Conference on Learning Representations(ICLR 2015). 2015.

[3] BIGGIO B, NELSON B, LASKOV P, et al. Poisoning attacks against support vector machines[C]//Proceedings of the 29th International Conference on Machine Learning(ICML 2012). 2012.

[4] XIAO H, BIGGIO B, BROWN G, et al. Is feature selection secure against training data poisoning? [J]. CoRR, abs /1804.07933, 2018.

[5] SHOKRI R, STRONATI M, SONG C Z, et al. Membership inference attacks against machine learning models[C]//2017 IEEE Symposium on Security and Privacy (SP 2017). 2017: 3-18.

[6] TRAM_ER F, ZHANG F, JUELS A, et al. Stealing machine learning models via prediction apis[C]//25th USENIX Security Symposium. 2016: 601-618.

[7] OH S J, AUGUSTIN M, FRITZ M, et al. Towards reverse-engineering black-box neural networks[C]//6th International Conference on Learning Representations(ICLR 2018). 2018.

[8] BATINA L, BHASIN S, JAP D, et al. CSI NN: reverse engineering of neural network architectures through electromagnetic side channel[C]//28th USENIX Security Symposium. 2019: 515-532.

[9] OREKONDY T, SCHIELE B, FRITZ M, et al. Knockoff nets: stealing functionality of black-box models[C]//IEEE Conference on Computer Vision and Pattern Recognition(CVPR 2019). 2019: 4954-4963.

[10] HUA W, ZHANG Z R, SUH G E. Reverse engineering convolutional neural networks through side-channel information leaks[C]// Proceedings of the 55th Annual Design Automation Conference (DAC 2018). 2018: 41-46.

[11] WEI L X, LUO B, LI Y, et al. I know what you see: Power side-channel attack on convolutional neural network accelerators[C]//Proceedings of the 34th Annual Computer Security Applications Conference. 2018: 393-406.

[12] HU X, LIANG L, DENG L, et al. Neural network model extraction attacks in edge devices by hearing architectural hints[J]. CoRR, abs/1903.03916, 2019.

[13] HAN S, MAO H Z, DALLY W J. Deep compression: compressing deep neural networks with pruning, trained quantization and human coding[C]//ICLR 2016. 2016.

[14] JACOB B, KLIGYS S, CHEN B, et al. Quantization and training of neural networks for efficient integer- arithmetic-only inference[C]// 2018 IEEE Conference on Computer Vision and Pattern Recognition(CVPR 2018). 2008: 2704-2713.

[15] RASTEGARI M, ORDONEZ V, REDMON J, et al. Xnor-net: Imagenet classification using binary convolutional neural networks[J]. CoRR, abs/1603.05279, 2016.

[16] PATIL N, JOUPPI N P, YOUNG C, et al. In-datacenter performance analysis of a tensor processing unit[C]//Proceedings of the 44th Annual International Symposium on Computer Architecture(ISCA 2017). 2017: 1-12.

[17] KOCHER P C. Timing attacks on implementations of Diffie-Hellman, RSA, DSS, and other systems[C]//Advances in Cryptology | CRYPTO '96. 1996: 104-113.

[18] MANGARD S. A simple power-analysis (spa) attack on implementations of the AES key expansion[C]//International Conference on Information Security and Cryptology(ICISC 2002). 2002: 343-358.

[19] KOCHER P, JAFFE J, JUN B. Differential power analysis[C]//Advances in Cryptology(CRYPTO' 99). 1999: 388-397.

[20] BRIER E, CLAVIER C, OLIVIER F. Correlation power analysis with a leakage model[C]//Cryptographic Hardware and Embedded Systems(CHES 2004). 2004: 16-29.

[21] KRIZHEVSKY A. One weird trick for parallelizing convolutional neural networks[J]. CoRR, abs/1404.5997, 2014.

[22] HE K, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition(CVPR 2016). 2016: 770-778.

[23] KRISHNAMOORTHI R. Quantizing deep convolutional networks for efficient inference: a whitepaper[M]. CoRR, abs/1806.08342, 2018.

[24] LIN D D, SACHIN S, TALATHI V, et al. Fixed point quantization of deep convolutional networks[C]//Proceedings of the 33nd International Conference on Machine Learning(ICML 2016). 216: 2849-2858.

Using side-channel and quantization vulnerability to recover DNN weights

LI Jinghai1, TANG Ming1,2, HUANG Chengxuan1

1.Key Laboratory of Aerospace Information Security and Trusted Computing, Ministry of Education, School of Cyber Science and Engineering, Wuhan University, Wuhan 430072, China 2. State Key Laboratory of Cryptology, Beijing 100878, China

AI security, model extraction attack, quantization vulnerability, side-channel analysis, Cluster-based SCA

TP309.2

10.11959/j.issn.2096−109x.2021038

2020−07−23；

2021−01−20

唐明，m.tang@126.com

国家自然科学基金（61972295）；武汉市科技项目应用基础前沿专项（2019010701011407）

The National Natural Science Foundation of China (61972295), The Frontier Applied Basic Research Project of Science and Technology Department of Wuhan (2019010701011407)

李景海, 唐明, 黄诚轩. 基于侧信道与量化推理缺陷的模型逆向攻击[J]. 网络与信息安全学报, 2021, 7(4):53-67.

LI J H, TANG M, HUANG C X. Using side-channel and quantization vulnerability to recover DNN weights[J]. Chinese Journal of Network and Information Security, 2021, 7(4): 53-67.

李景海（1996−），男，重庆人，武汉大学硕士生，主要研究方向为侧信道与AI安全。