基于SM9算法的部分盲签名方案

2021-09-08吕尧侯金鹏聂冲苏铓王彬蒋鸿玲

网络与信息安全学报 2021年4期

吕尧，侯金鹏，聂冲，苏铓，王彬，蒋鸿玲

基于SM9算法的部分盲签名方案

吕尧1，侯金鹏2，聂冲2，苏铓2，王彬3，蒋鸿玲3

（1. 中国电子信息产业发展研究院，北京 100048；2. 南京理工大学计算机科学与工程学院，江苏南京 210094；3. 北京信息科技大学信息管理学院，北京 100192）

普通的数字签名在有效保护用户隐私方面存在诸多不足，如对签名的抵赖和跟踪时有发生。针对上述问题，提出一种基于SM9算法的部分盲签名方案，部分是指签名消息包含用户的消息和其他有关信息，能够有效抵抗签名抵赖和跟踪，同时引入可信第三方来防止恶意用户对信息的篡改。通过实验结果和理论分析，证明了所提算法的安全性和高效性。

SM9算法；盲签名；部分盲签名；数字签名

1 引言

在信息化时代，消息得以快速传播，特别是随着5G时代的到来，物联网应用的发展越来越迅速。这便利了人们的生活，但也带来了许多潜在的安全威胁：数据在开放的网络环境下传输，难免会遭到不法分子的恶意攻击，使隐私数据非法泄露或被篡改。物联网、5G通信应用快速发展的同时，用户隐私数据被攻击、截获甚至破解的安全风险逐渐增加。这些安全风险不仅可能造成个人或企业的经济损失，甚至可能威胁到国家的安全。SM9算法和部分盲签名在此背景下显示出极大的发展潜力。

Koblitz[1]、Miller[2]分别于1984年、1986年提出了基于椭圆曲线的公钥密码算法，在安全性相同的条件下，可以使用比其他公钥密码算法更短的密钥。1984年，Shamir[3]提出标识密码（IBE）的概念，简化了密钥管理环节。2000年，Sakai[4]提出基于椭圆曲线和双线性对的密码系统。2001年，Boneh和Franklin[5]提出使用Weil对构造标识公钥加密算法。2016年，国家密码管理局发布了SM9密码算法标准[6]。SM9算法简化了密钥管理环节，可以大大减少申请和验证过程，特别适合海量用户的安全交互通信。

Chuam[7]于1983年首次提出盲签名概念，通过对签名消息的盲化来达到隐私保护的效果。盲签名比普通的数字签名更能保护用户的隐私。但签名消息对签名者的完全匿名性也带来了安全隐患，签名会被非法分子滥用。为了使签名者在不知道所签消息的同时能在必要时对该签名可控，Brands[8]提出一种受限盲签名方案，但该方案在验证时需要与消息提供者交互。为了克服该问题，1996年，Abe等[9]提出一个部分盲签名的简单模型，部分盲签名通过在签名中嵌入用户与签名者协商的公共信息，避免了完全匿名留下的安全隐患。但部分盲签名的方案易存在公共信息被替代的漏洞[10]。如2013年，汤志鹏等[11]发现余丹等[12]的方案存在公共信息可以被非法篡改的漏洞；何俊杰等[13]分析了文献[11]的方案，也存在恶意用户可以非法篡改公共信息的缺陷；杨俊芳[14]分析文献[13]方案发现，同样存在公共信息被篡改的可能。

现有的基于SM9算法的盲签名仅有两个方案：一是张雪峰和彭华提出的一种基于SM9算法的盲签名方案研究[15]，二是何德彪等提出的一种基于SM9数字签名的盲签名生成方法与系统[16]。

文献[15]提出的基于SM9算法的盲签名方案分为消息盲化、签名生成和签名验证3个步骤。通过对消息进行盲化，将盲化后的消息传给签名者进行签名，实现了消息的隐私保护。该方案存在的问题：签名时使用杂凑函数对盲化后的消息′进行单向压缩运算，因此实际得到的是盲化消息′的签名而非待签消息的签名。

文献[16]提出一种基于SM9数字签名的盲签名方案，可以在签名者不知道真实消息的情况下生成正确的SM9盲签名。签名的过程由签名者和用户共同执行，生成SM9盲签名的过程不会向签名者泄露被签名的消息，既能保证签名的正确性，又能保证签名消息的隐私性，是一种实用的盲签名算法。

本文在文献[16]的基础上设计一种基于SM9数字签名算法的部分盲签名方案，在签名中植入关于时间的公共信息，在保证用户消息隐私的情况下，使签名具有可控性，同时，算法中的公共信息无法被非法篡改。本文算法可以应用的范围比盲签名更广，如电子现金、电子拍卖、电子投票等领域。

2 基础知识

本节介绍盲签名和部分盲签名的概念，同时介绍一些相关的数学理论。

2.1 盲签名与部分盲签名

盲签名即签名者不知道所签消息的内容，签名后不能对自己的签名抵赖和进行跟踪的一种特殊的数字签名。相比普通的数字签名，盲签名能够更好地保护用户的隐私。基于这一优点，盲签名被广泛应用于电子投票等需要保护自身隐私的场合。

但是，盲签名的完全盲化带来了不可控性，这使它更容易被非法分子滥用。为了解决这个额外风险，产生了部分盲签名。在部分盲签名方案中，签名者在签名时可以加入与用户协商的消息或者自己的信息。消息提供者不能篡改签名者加入的信息，从而阻止签名申请者提供非法信息或篡改信息而滥用签名，这样既有效地保护了用户的隐私又让签名者对所签署的内容部分可控。

2.2 有限域上的椭圆曲线

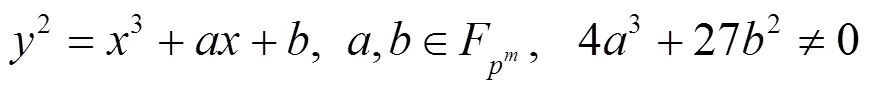
2.3 双线性对

3 本文方案

本文提出的基于SM9数字签名算法的部分盲签名方案，在保证消息盲化的同时可以确定最后生成的签名是对于消息的部分盲签名。对于其他学者提出的部分盲签名方案中出现的公共信息被篡改漏洞，本文设计的部分盲签名方案通过引入可信任第三方对公共信息是否被篡改进行验证，能在一定限度上防止公共消息被篡改。

3.1 系统参数组

SM9算法的主要参数及参数说明如表1 所示。

3.2 主密钥对与用户私钥的产生

由密钥生成中心KGC产生主密钥对(，pub)及用户的签名私钥dsa，具体步骤与SM9算法主密钥对和用户私钥的产生一致。

3.3 部分盲签名生成算法

（1）签名准备

签名前，向可信任第三方申请一个关于签名有效期的公共信息（timeh, endt），详细描述如下。

表1 系统参数

签名开始前向可信第三方发出申请，第三方收到申请后：

a. 获取当前时间戳，并将其与预先设置有效期相加获得有效期时间戳endt；

d. 将endt与timeh的数据类型转换为字节串，签名中的公共消息为（timeh, endt）。

（2）公共参数计算

（3）盲化

（4）签名

（5）解盲

3.4 部分盲签名验证算法

部分盲签名的验证算法根据被验证对象的不同分为两部分：一是时间戳的验证，包括第三方对公共信息是否被篡改的验证和验证方对签名是否在有效期内的验证；二是部分盲签名正确性的验证。

（1）时间戳的验证

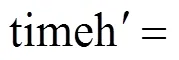
b. 验证者从第三方获得公共信息是否被篡改的结果，如果被告知公共信息被篡改，则签名验证不通过，否则进行部分盲签名的正确性验证。若签名验证正确，进行签名有效期验证：验证者获取当前时间戳，与endt进行时间戳大小比较，若当前时间戳大于endt，则验证不通过，否则验证通过。

2. 盲签名正确性的验证

为了检验收到的消息的正确性与完整性，需要验证部分盲签名（,, timeh, endt）的正确性，作为验证者的用户应实现以下运算步骤：

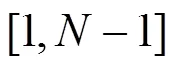
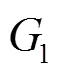
3.5 方案的正确性证明

本文提出的基于SM9算法的部分盲签方案是可验证正确的。证明如下。

盲签名过程中

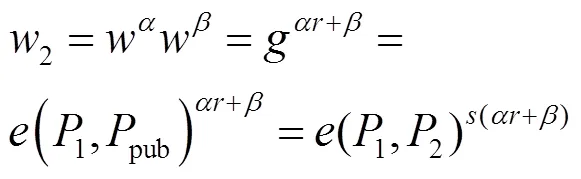
4 实验分析

本节从安全性、正确性和效率3方面分析所提部分盲签名算法。

4.1 安全性分析

部分盲签名算法的安全性包括不可伪造性和盲性，不可伪造性是指签名结果不能被任意攻击方伪造，盲性是指签名的消息不被除消息拥有者外的任何人知道。本节分别给出二者的定义和证明。

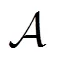
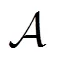
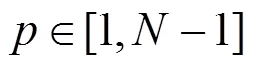
4.2 正确性测试

本文实现的算法中SM9的参数使用《GMT 0044-2016 SM9标识密码算法》。

本节测试算法的主密钥对和用户私钥的生成功能、签名验签功能，其中盲签名的验证测试分为正确性测试和时间戳验证测试。以下测试是在程序中定义了一个宏#define SELF_CHECK 1的情况下进行的，即在本次测试中除结束时间戳，其他随机数均采用预设的值。

主私钥为文献[10]中数字签名算法示例所规定的值，为0130e7 8459d785 45cb54c5 87e02cf4 80ce0b66 340f319f 348a1d5b 1f2dc5f4。

输入主公钥与用户私钥，测试消息为Chinese IBS standard。测试结果如图1所示。

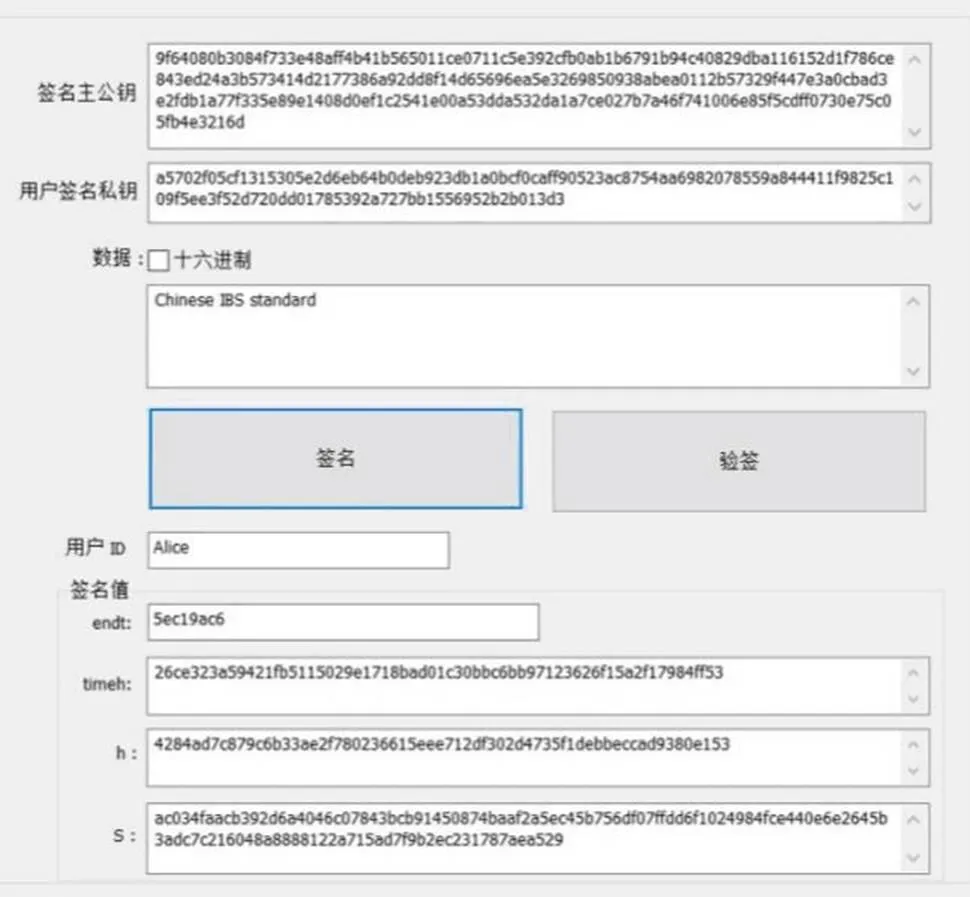
图1 盲签名结果

Figure 1 Blind signature result

对算法验证环节中的各种异常情况进行测试的结果如表2所示，可以看出，本文的算法可以将恶意篡改错误信息的敌手与正常用户区分出来。

表2 正确性测试

4.3 效率测试

在Intel(R) Core(TM) i5-10210U CPU @ 1.60 GHz 2.11 GHz的处理器上运行本文算法（下文简称PBS）和参考文献[12]算法，测试结果如表3所示。

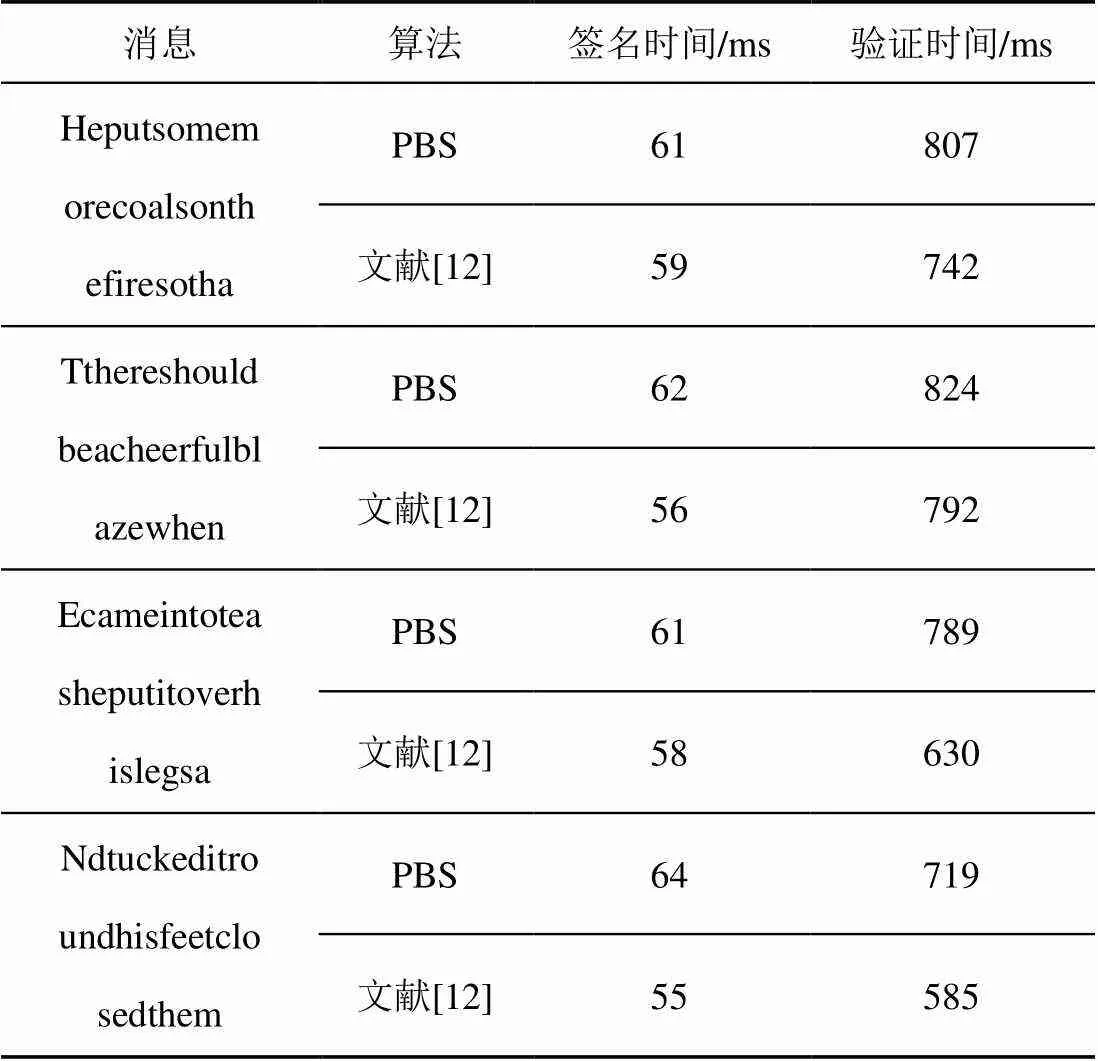
表3 效率测试

从表3可以看出，本文算法在不计算与可信第三方通信时间的情况下，与文献[12]算法在运行时间上处于相同数量级。

5 结束语

本文提出了一种基于SM9数字签名算法的部分盲签名方案。在保证用户消息隐私的情况下，必要时可以通过公共信息追踪用户身份，与何德彪等提出的盲签名方案[12]相比，避免了完全盲性。本文主要论述了方案中的盲签名生成与验证算法以及相关密钥生成算法，并从盲签名、时间戳两个方面进行了正确性验证和分析，通过编程测试验证了该方案的主密钥对、用户私钥、部分盲签名生成算法以及验签算法。本文方案可以为电子现金、电子投票、电子拍卖等系统中的盲签名[22-23]额外提供时效性与可控性，是一个很有应用前景的方案。

[1] KOBLITZ N I. Introduction to elliptic curves and modular forms[M]. Springer Science & Business Media, 2012.

[2] MILLER V S. Use of elliptic curves in cryptography[C]// Conference on the Theory and Application of Cryptographic Techniques. Springer, Berlin, Heidelberg, 198: 417-426.

[3] SHAMIR A. Identity-based cryptography and signature schemes[C]// Proceedings of CRYPTO'84. 1984.

[4] SAKAI R. Cryptosystems based on pairing[C]//SCIS2000. 2000.

[5] BONEH D, FRANKLIN M. Identity-based encryption from the Weil pairing[C]//Annual International Cryptology Conference. 2001: 213-229.

[6] 袁峰, 程朝辉. SM9 标识密码算法综述[J]. 信息安全研究, 2016, 2(11): 1008-1027.

YUAN F, CHENG C H. A survey of SM9 identity cryptography algorithms[J]. Research on Information Security, 2016, 2(11): 1008-1027.

[7] CHAUM D. Blind signatures for untraceable payments[J]. Advances in Cryptology, 1983: 199-203.

[8] BRANDS S. Restrictive binding of secret-key certificates[C]//International Conference on the Theory and Applications of Cryptographic Techniques. 1995: 231-247.

[9] ABE M, FUJISAKI E. How to date blind signatures[C]//International Conference on the Theory and Application of Cryptology and Information Security. 1996:244-251.

[10] GMT 0044-2016 SM9标识密码算法：第5部分参数定义[R].

GMT 0044-2016 SM9 identity cipher algorithm: part 5 Parameter Definitions[R].

[11] 汤志鹏, 李晓雄, 左黎明, 等. 高效安全无证书部分盲签名[J]. 计算机工程与设计, 2013, 34(02): 339-446.

TANG Z P, LI X X, ZUO L M, et al. Efficient, secure, certificateless partial blind signature[J]. Computer Engineering and Design, 2013, 34(02): 339-446.

[12] 余丹, 杨晓元, 黄大威. 新的无证书部分盲签名方案[J]. 计算机应用研究, 2010, 27(11): 4319-4321.

YU D, YANG X Y, HUANG D W. A new certificateless partial blind signature scheme[J]. Computer Application Research, 2010, 27(11): 4319-4321.

[13] 何俊杰, 张帆, 绍辉. 对一个无证书部分盲签名方案的分析与改进[J]. 信阳师范学院学报: 自然科学版, 2014, 27(2): 170-175.

HE J J, ZHANG F, SHAO H. Analysis and improvement of a certificateless partial blind signature scheme[J]. Journal of Xinyang Normal University: Natural Science Edition, 2014, 27(2): 170-175.

[14] 杨俊芳. 部分盲签名研究及其应用[D]. 南昌: 华东交通大学, 2016.

YANG J F. Research and Application of partial Blind signature[D]. Nanchang: East China Jiaotong University, 2016.

[15] 张雪锋, 彭华. 一种基于 SM9 算法的盲签名方案研究[J]. 信息网络安全, 2019, 19(8): 61-67.

ZHANG X F, PENG H. Research on a Blind signature scheme based on SM9 algorithm[J]. Information Network Security, 2019, 19(8): 61-67.

[16] 何德彪, 张语荻, 张宇波, 等. 一种基于SM9数字签名的盲签名生成方法及系统:中国, CN201810333911.4[P]. 2018-04-13.

HE D B, ZHANG Y D, ZHANG Y B, et al. A blind signature generation method and system based on SM9 digital signature: China, CN201810333911.4[P]. 2018-04-13.

[17] 苏志图. 双线性对的快速计算研究[D]. 西安: 西安电子科技大学, 2012.

SU Z T. Study on the fast calculation of bilinear pairs[D]. Xi'an: Xi'an University of Electronic Science and Technology. 2012.

[18] 赵昌安. 双线性对的有效计算[D]. 广州:中山大学, 2008.

ZHAO C A. Efficient calculation of bilinear pairs[D]. Guangzhou: Sun Yat-sen University. 2008.

[19] 赵昌安, 张方国. 双线性对有效计算研究进展[J]. 软件学报, 2009, 20(11): 3001-3009.

ZHAO C A, ZHANG F G. Research progress of bilinear pair effective computation[J]. Journal of Software, 2009, 20(11): 3001-3009.

[20] 李彬, 王新梅. 高效的R-ate对的参数构造方法[J]. 通信学报, 2010, 31(1): 118-121.

LI B, WANG X M. An efficient parameter construction method for R-ate pairs [J]. Journal on Communication, 2010, 31(1): 118-121.

[21] 甘植旺, 廖方圆. 国密SM9中R-ate双线性对快速计算[J]. 计算机工程, 2019, 45(6): 171-174.

GAN Z W, LIAO F Y. Fast calculation of R-ate bilinear pairs in national secret SM9[J]. Computer Engineering. 2019, 45(6): 171-174.

[22] 张骁, 周清雷, 李斌. 基于HRCA的可重构SM4密码算法研究与实现[J]. 网络与信息安全学报, 2020, 6(5): 101-109.

ZHANG X, ZHOU Q L, LI B. Research and implementation of Reconfigurable SM4 cryptographic algorithm based on HRCA[J]. Journal of Network and Information Security, 2020, 6(5): 101-109.

[23] 吴邱涵, 胡卫. 基于SM2算法和区块链的移动端身份认证协议设计[J]. 网络与信息安全学报, 2018, 4(9): 60-65.

WU Q H, HU W. Design of mobile authentication protocol based on SM2 algorithm and block chain[J]. Journal of Network and Information Security, 2018, 4(9): 60-65.

Partial blind signature scheme based on SM9 algorithm

LYU Yao1, HOU Jinpeng2, NIE Chong2, SU Mang2, WANG Bin3, JIANG Hongling3

1. China Center for Information Industry Development, Beijing 100048, China 2. School of Computer Science and Engineering, Nanjing University of Science and Technology, Nanjing 210094, China 3. School of Information Management, Beijing Information Science & Technology University, Beijing 100192, China

Ordinary digital signatures have many deficiencies in effectively protecting users' privacy, and signature repudiation and tracking occur from time to time. In order to solve the above problems, a partial blind signature scheme based on the SM9 algorithm was proposed. Partially means that the signature message contains the user's message and other related information, so it can effectively resist signature repudiation and tracking, and introduce a trusted third party to prevent malicious users from tampering with information. Through experimental results and theoretical analysis, the security and efficiency of the proposed algorithm are proved.

SM9 algorithm, blind signature, partial blind signature,digital signature

TP393.08

10.11959/j.issn.2096−109x.2021037

2020−09−29；

2020−12−31

苏铓，sumang@njust.edu.cn

国家自然科学基金（61702266）

The National Natural Science Foundation of China (61702266)

吕尧, 侯金鹏, 聂冲, 等. 基于SM9算法的部分盲签名方案[J]. 网络与信息安全学报, 2021, 7(4): 147-153.

LYU Y, HOU J P, NIE C, et al. Partial blind signature algorithm based on SM9[J]. Chinese Journal of Network and Information Security, 2021, 7(4): 147-153.

吕尧（1984−），男，陕西宝鸡人，中国电子信息产业发展研究院助理研究员，主要研究方向为信息安全、电子认证领、密码、数据安全和个人信息保护。