具有时滞和单反馈控制变量的偏利合作系统的Hopf分支

王月月，吕堂红，周林华

(长春理工大学 理学院，吉林 长春130022)

0 引 言

偏利共生关系在生态学中描述的是对一方有利而对另一方既无利也无害的共生类型. 例如，兰花依附在乔木枝干的表面，使自己更易获得阳光和空气中的水分，而对乔木本身却无影响. 虽然这种生物现象很常见，但是直到2003年，孙广才等[1]才根据Lotka-Volterra竞争系统提出了针对偏利共生的生物模型，随后，祝占法等[2]提出了一方不能独立生存的两种群偏利合作模型，分析了污染中偏利共生的两种群持续生存与绝灭的阈值.

生态系统不断受到不可预测的力量干扰，这会导致某些生物参数发生改变，如存活率[3]. 为了更准确地描述这种干扰，学者们引入了反馈控制变量，文献[4-9]讨论了具有反馈控制变量的系统的动力学性质. 2018年，杨英钟等[10]研究了具反馈控制的一方不能独立生存的偏利合作系统

(1)

式中：bi,aij,η,fi(i,j=1,2)均为正常数.xi(i=1,2)表示种群在t时刻的生长密度，ui(i=1,2)表示反馈控制变量，b1,b2表示种群x1,x2的内禀增长率，aii(i=1,2)表示两种群的密度制约系数.研究结果表明，不适当的反馈控制变量将导致系统中不能独立生存的种群x1绝灭.

在自然界中一种控制策略会对多个物种产生影响. 例如，在农业生产中，喷洒农药可以减少杂草的数量，但同时也对农作物或相关动物的生长产生负面影响. 2015年，韩荣玉等[11]讨论了具有单反馈控制变量的Lotka-Volterr合作系统的稳定性，分析得到在适当限制反馈控制变量系数的情况下，系统仍然可以保持全局稳定或灭绝. 注意到，对于加入反馈控制变量后的模型，学者们研究的多是反馈控制变量对于系统稳定性、 持久性、 绝灭性等的影响，而并没有考虑在模型中加入时滞项，并证明其分支存在性以及研究其分支周期解稳定性的研究成果. 因此，笔者在模型(1)的基础上，考虑单反馈控制变量对于偏利合作系统的影响，同时引入种群x2的妊娠时滞τ，提出具有单反馈控制变量和时滞的偏利合作系统

(2)

式中：τ表示种群x2的妊娠期；u表示反馈控制变量；其他参数意义同模型(1).

1 局部稳定性和Hopf分支

(3)

因此，有

于是，当

(H1)：a12η>a1f2;b2(a12η-a1f2)>b1(a22·η+a2f2)成立时，系统(2)存在唯一正平衡点.

系统(2)在正平衡点E*处的Jacobi矩阵为

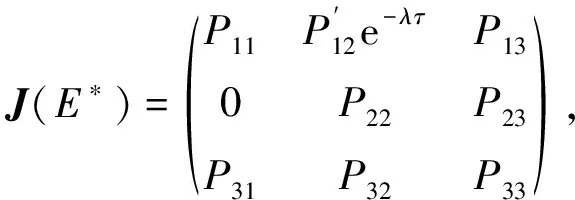
(4)

其中

P32=f2,P33=-η.

于是，系统(2)在正平衡点E*处的特征方程为

λ3+P1λ2+P2λ+P3+P4e-λτ=0,

(5)

其中

P1=-(P11+P22+P33);

P2=P11P22+P11P33+P22P33-P13P31-P23P32;

P3=P13P22P31+P11P23P32-P11P22P33;

当τ=0时，式(5)变为

λ3+P1λ2+P2λ+P3+P4=0.

(6)

又因为P1>0,假设

(H2)P3+P4>0；

(H3)P1P2>P3+P4.

由Hurwitz判据知，方程(6)的所有根均具有负实部.

当τ≠0时，令λ=iω(ω>0)为(5)的一个根，分离实部与虚部，有

(7)

两边同时平方相加得到

(8)

令v=ω2，则式(8)变为

v3+m1v2+m2v+m3=0,

(9)

引理1对于式(9)，有如下结果：

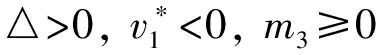
k=1,2,3;i=0,1,2,….

(10)

经计算有

(11)

假设

(H6)f′(v)≠0.

由上述讨论，可得以下结论：

定理1对于系统(2)，如果(H1)～(H3)成立，则有

1) 若满足(H4)，则当τ∈[0,τ0)时，则E*(x*,y*,u*)是局部渐近稳定的；

2) 若满足(H5)和(H6)，则当τ>τ0时，E*(x*,y*,u*)是不稳定的；当τ=τ0时，系统(2)在E*(x*,y*,u*)处产生Hopf分支.

2 局部Hopf分支方向及其稳定性

下面研究在τ≠0条件下，运用Hassard[12]的中心流形定理和规范型方法，得到决定系统(2)的Hopf分支性质的表达式.

令u(t)=(u1(t),u2(t),u3(t))T∈R3，u1(t)=x1(τt)，u2(t)=x2(τt)，u3(t)=u(τt)，τ=τ0+μ,μ∈R，则系统(2)在C=C([-1,0],R3)上变为一般的泛函微分方程

(12)

(13)

F(μ,φ)=(τ0+μ)(F1(μ,φ),F2(μ,φ),F3(μ,φ))T,

(14)

因此，由Riesz表示定理，能找到一个有界变差的三阶矩阵

η(θ,μ)∶[-1,0]→R3，

使得

这里

其中，δ(θ)是Dirac-delta函数.

对于φ∈C1([-1,0],R3)，定义

于是，系统(12)可改写为

(15)

式中：u=(u1,u2,u3);ut(θ)=u(t+θ),θ∈[-1,0].

对于ψ∈C1([-1,0],(R3)*)，定义A=A(0)的伴随算子A*为

和一个双线性型

θ)dη(θ)φ(ξ)dξ.

设A和A*对应于特征根iω0τ0与-iω0τ0的特征向量分别为q(θ)和q*(s). 于是

A(0)q(θ)=iω0τ0q(θ)，

A*(0)q*(s)=-iω0τ0q*(s).

通过计算，可以得到

这里

下面计算在μ=0处的中心流形C0，令Xt为μ=0时，方程(15)的解. 定义

z(t)=〈q*,Xt〉，W(t,θ)=Xt(θ)-2Rez(t)q(θ).

(16)

在中心流形C0上，有

(17)

记

其中

(18)

由(16)和(17)得到

Xt(θ)=W(t,θ)+2Re{z(t)q(θ)}=

综合(14)得到

与式(18)比较系数，得到

为了确定g21，下面计算W20(θ),W11(θ). 由式(15)和式(16)得到

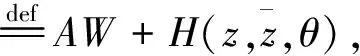
(19)

其中

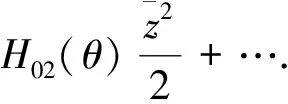
(20)

结合式(16)和式(17)，将式(20)代入到式(19)中，比较系数，得到

(2iω0τ0-A)W20(θ)=H20(θ),

-AW11(θ)=H11(θ).

由式(19)易知，当θ∈[-1,0)时

(21)

比较式(20)和式(21)，有

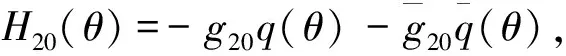
(22)

(23)

因此，

类似地，有

因此，可以得到

(24)

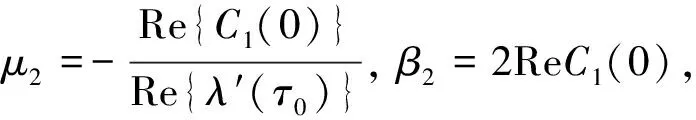
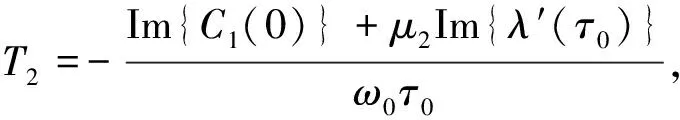
(25)

式中：C1(0)由式(24)给出，易得出μ2，β2，T2的值.因此，有

定理2当τ=τ0时，式(25)的各个表达式决定了分支周期解在中心流形上的性质，因此，得出下面的结论：

1)μ2确定Hopf分支的方向.如果μ2>0(μ2<0)，则分支周期解为前向(后向)；

2)β2确定分支周期解的稳定性.如果β2<0(β2>0)，则分支周期解是稳定的(不稳定的)；

3)T2确定分支周期解的周期.如果T2>0(T2<0)，则分支周期解的周期增大(减小).

3 数值模拟

为了验证上面分析所得的理论结果，选择适当的参数，考虑以下系统

(26)

不难验证(H1)～(H3)、 (H5)～(H6)成立，此时得到系统(26)的正平衡点为

E*(0.2245,0.6649,1.3362).

通过计算得到ω0≈0.363 3，τ0≈5.126 7，C1(0)≈-0.150 5-0.857 0i，μ2≈0.072 9>0，β2≈-0.301 0<0，T2≈12.154 3>0.

当τ=4.8<τ0≈5.126 7时，由图1 可知，系统(26)的正平衡点E*是局部渐近稳定的； 当τ=5.8>τ0≈5.126 7时，由图2 可知，系统(26)的正平衡点E*是不稳定的.由定理 2 可知，关于τ>τ0时的Hopf分支是前向分支，分支周期解是稳定的且其周期增加.

(a) 种群x1的波图

(b) 种群x2的波图

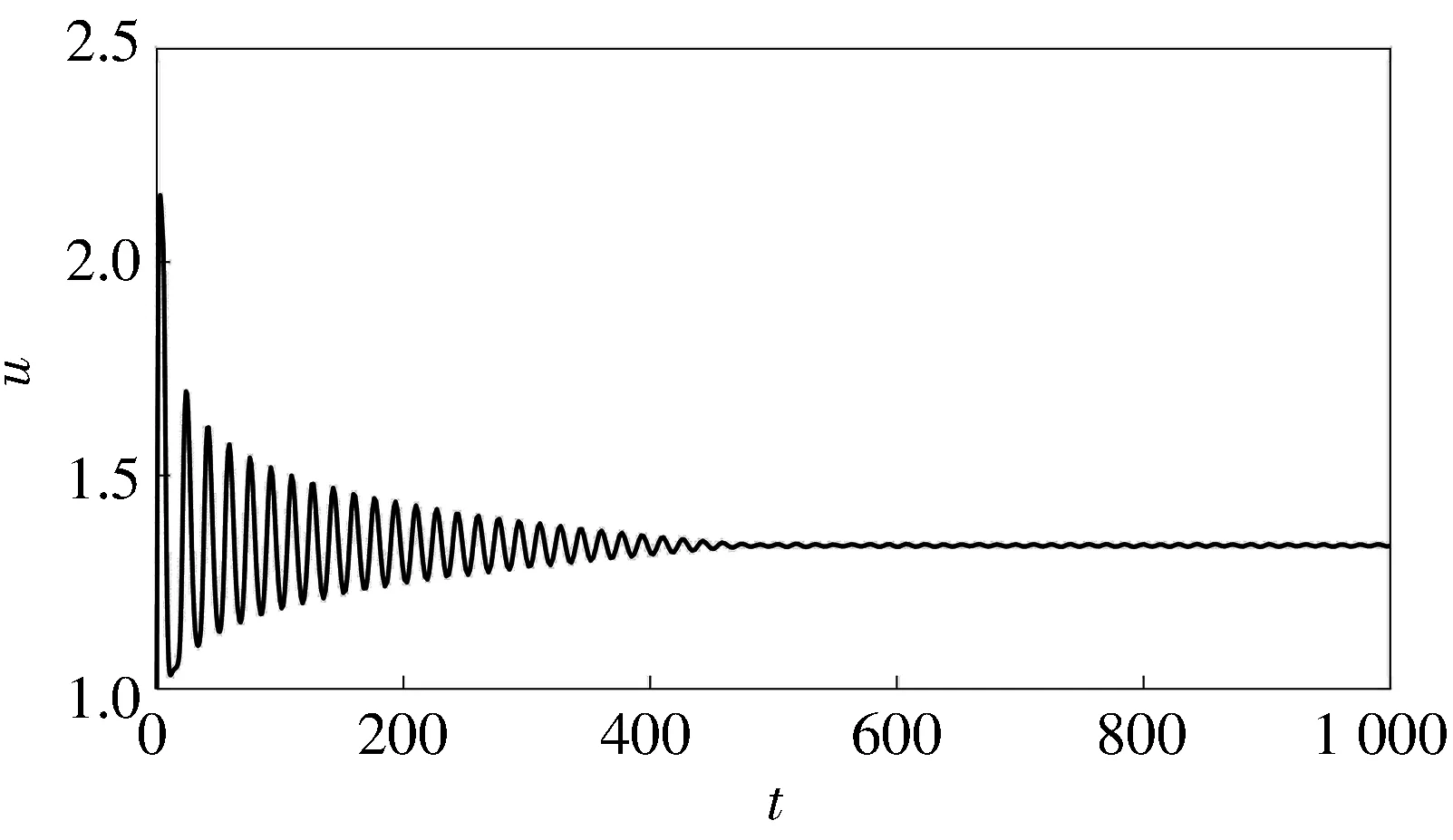
(c) 反馈控制变量u的波图

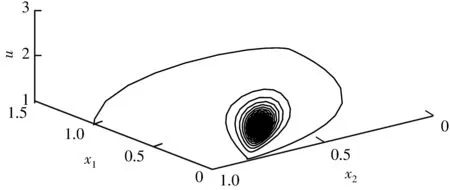
(d) 系统(26)的相图

(a) 种群x1的波图

(b) 种群x2的波图

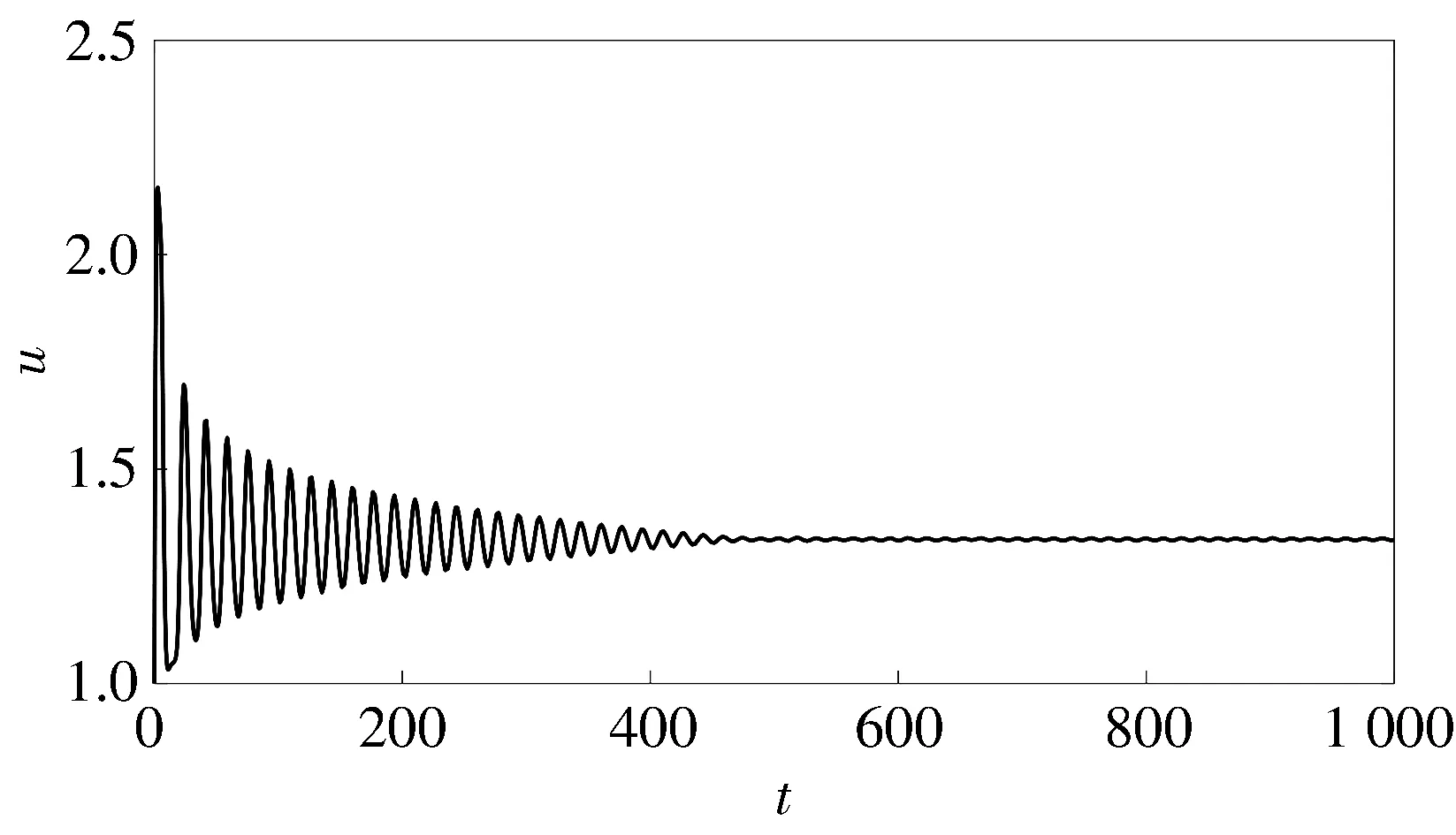
(c) 反馈控制变量u的波图

(d) 系统(26)的相图

4 结 论

本文研究了一类具有时滞和单反馈控制变量的偏利合作系统的动力学行为，考虑了种群x2的妊娠期时滞以及单反馈控制变量对偏利合作系统的种群密度的影响. 研究结果表明，时滞变化对具有单反馈控制变量的偏利合作系统的正平衡点的局部稳定性产生影响，当分支数值在适当的范围内，系统的正平衡点是局部渐近稳定的；而当时滞超过临界值时，系统的正平衡点是不稳定的，且发生Hopf分支并产生周期解.