基于PSO-CV算法的信息扩散插值模型及其在黄河源区的应用

2021-09-08黄华平尹开霞靳高阳

人民珠江 2021年9期

黄华平，尹开霞，靳高阳

(中水珠江规划勘测设计有限公司，广东广州 510610)

准确的降水空间分布信息是理解不同尺度范围内水量及能量变化过程的前提条件，对于区域水文水资源分析及管理、洪涝灾害预测及防治和生态环境治理等关键问题具有重要意义[1]。根据有限的雨量站观测资料进行空间插值是探索降水空间特征的有效手段，也是当前水科学研究的热点问题[2-5]。

目前，针对降水的空间插值已有大量研究，依据其原理可以大致分为三类，包括“确定性插值方法”“空间统计学方法”及“其他方法”[6]。确定性空间插值方法中最具代表性的是泰森多边形法、等雨量线法及反距离加权法[7-8]。这类方法一般采用均化处理来描述降水空间特征变化，以便水文模型的产流计算。其特点是原理简单且运算速度快，但结果易受控于距离较近的站点[9]。而空间统计学方法则以区域化变量为基础，致力于利用相邻观测点间的相互关系来对未知点进行估计[10]。克里金法与其变种方法均属于此范畴内。该类方法具有坚实的科学理论基础，因此较之确定性插值方法受到更广泛的重视。但其缺点也不容忽视，如原理复杂且假设过于理想化、理论半变异函数选取主观化及结果易产生“平滑效应”等[11]。第三类是基于非线性科学理论的插值方法，充分考虑了降水具有随机性与模糊性的双重特征，并以此对降水空间特征进行刻画，具体包括了信息熵法、贝叶斯最大熵法、互信息理论及信息扩散理论等理论方法[12-14]。该类方法无需过多的理论假设，且能提供更多的降水空间信息，但与前两者相比，相关研究较少。

本文介绍了一种基于信息扩散理论的空间插值模型，针对模型中的关键参数-窗宽值，考虑已有经验公式法难以合理估计偏态分布样本参数的不足，提出了一种粒子群算法与交叉验证相结合的最优窗宽估计方法。研究以黄河源区为例，在综合分析流域降水空间分布特征的基础上，分别对2种信息扩散插值模型关于年、季、月及日降水量的插值精度进行评估，并引入了4种常用的空间插值方法作为参照。

1 方法

1.1 信息扩散插值模型

记M={X,Y}为雨量随机场，X为任意点位置，Y为该点降水量。假定该随机场内存在分布函数f(X,Y)，其反映了空间内的降水信息分布密度，则降水量Y=yj关于观测点X=xi的条件密度函数依据全概率公式可表示为：

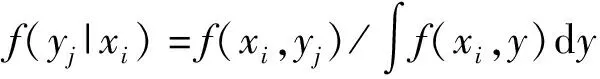
(1)

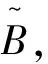
(2)

最终，对隶属度函数进行去模糊化即可得到对应估计值，见式(3)：

(3)

由式(1)—(3)不难发现，该模型重点在于如何估计降水信息分布密度函数f(X,Y)。基于雨量站点观测资料m={xi,yi,i=1,2,…,n}(n为雨量站数量)，可采用信息扩散理论对该密度函数进行无偏估计，见式(4)：

(4)

式中，hx与hy分别为X与Y维度对应的窗宽值。

最终，将式(4)代式(1)—(3)中，即可确定雨量随机场内任意点处降水量隶属度函数，并实现降水插值计算。

1.2 参数估计方法

确定上述插值模型后，还需估计模型内关键参数——窗宽值。目前，已有估计方法存在结果非最优参数或原理过于复杂等问题[13,15-16]。因此，本文简要介绍其中的经验窗宽公式法，并提出一种基于粒子群算法与交叉验证相结合的最优窗宽估计方法。该方法较之已有方法无过多繁琐公式推导，且插值精度较高。

1.2.1经验窗宽公式法

基于“平均距离模型”与“两点择近原则”，黄崇福[17]推导了窗宽h的经验计算公式。

(5)

式中，a=min(li)；b=max(li)；i=1,2,…,n。不难看出，窗宽大小仅与观测样本的数量、各维度上最大值和最小值相关。

该方法具有计算快速且简便的优点，但其仅是对单变量扩散函数进行推导得到的，而对于插值过程中需要解决的多元问题，该方法并不能保证参数结果的最优性。并且当观测样本为非对称、非正态结构时，该参数估计方法将产生较大偏差。而降水在空间上往往服从偏态分布，因此采用经验窗宽公式法推求相关参数难免存在一定偏差。

1.2.2基于PSO-CV算法的最优窗宽估计法

为克服已有方法的不足，本文提出一种基于粒子群算法与交叉验证相结合的最优窗宽估计方法。该方法通过采用留一交叉验证法，逐一计算估计值与实测值间的绝对误差，并将整个过程中的绝对误差之和作为目标函数，采用粒子群算法对该目标函数进行最小寻优，具体步骤如下。

步骤一确定目标函数。累计每次“留一交叉验证法”估计值与实际值间的绝对误差，将其最小化作为算法的优化准则，见式(6)：

(6)

式中，Pobs(si)与Pest(si)分别为点si处的观测值与估计值。

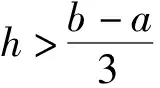
步骤三迭代更新。在迭代过程中，每个粒子依据历史所处的最优位置和整个群体的最优位置，结合随机扰动来确定下一步的移动，具体为：

(7)

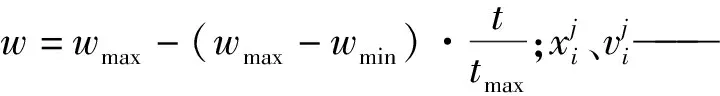
步骤四确定最优窗宽。当粒子群迭代到最大迭代次数时，即停止迭代计算。此时，选择目标函数最小值对应粒子的位置h=(h1,h2,…,hn)(n为待寻优参数个数)作为整个观测样本的最优窗宽值。

1.3 误差评价指标

a)均方根误差(RMSE)。RMSE值是实测数据和插值结果之间偏差平方均值的平方根，反映空间插值方法的精准度，其值越小，说明插值结果和实测数据越接近，计算公式为：

(8)

b)绝对偏差(ABIAS)。ABAIS值是插值结果与实测数据之间误差绝对值与实测数据均值的比值，反映了插值结果相对于实测数据的偏差程度，计算公式为：

(9)

c)相关系数(CC)。CC值描述了插值结果与实测数据之间的线性相关程度，其值越接近于1，表明两者相关性程度越高，计算公式为：

(10)

2 结果分析

本文以黄河源区为例，搜集了源区内及附近区域17个气象站和5个水文站1986—2015年逐日降水数据，源区基本概况及站点分布见图1。研究引入了反距离加权法(IDW)、普通克里金法(OK)，泛克里金法(DUK)及考虑高程的协克里金法(COK)作为对比参照，比较且评估了上述2种信息扩散插值模型，即经验信息插值模型(EMP)及基于PSO-CV算法的最优信息插值模型(OPT)。首先，研究对黄河源区多年平均年及各季降水量的空间分布特征进行了综合分析，在此基础上采用留一交叉验证法分别从年、季、月与日4种时间尺度对各空间插值方法的精度进行了比较与评价。

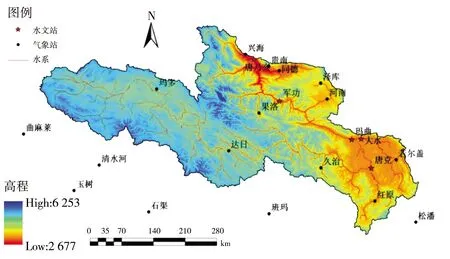
图1 研究区位置及水文、气象站点分布

2.1 源区降水特征分析

为比较不同插值方法结果的空间差异性，研究先将22个站点作为已知数据，对源区多年平均年及各季降水量的空间分布特征进行估计，考虑到流域面积较大，此次采用地区性插值法，即选取各未知点距离最近的10个站点进行插值估计。图2提供了不同方法对应多年平均年降水量空间分布，整体来看，6种方法刻画的年降水量空间分布特征基本相似，均呈现“南高北低，东高西低”的基本特征，年降水整体呈现带状分布，东南部降水量大，西北部降水量小。对比不同插值方法的空间分布特性，可以发现图2b克里金法和图2d协克里金法差异很小，而2种信息扩散插值方法除部分细节外，整体也较为类似。不同方法的主要差异在于源区西北部。具体来看，普通克里金法和协克里金法对应年降水量在该地区显著大于其他方法，而2种信息扩散插值方法对于该地区的估计值则小于其他方法。对比2种信息扩散插值方法，可以发现图2f最优信息插值模型在西北区域和东南区域均略大于图2e经验信息插值模型。考虑到文章篇幅，其他季节降水量的空间分布未展示在本文中。

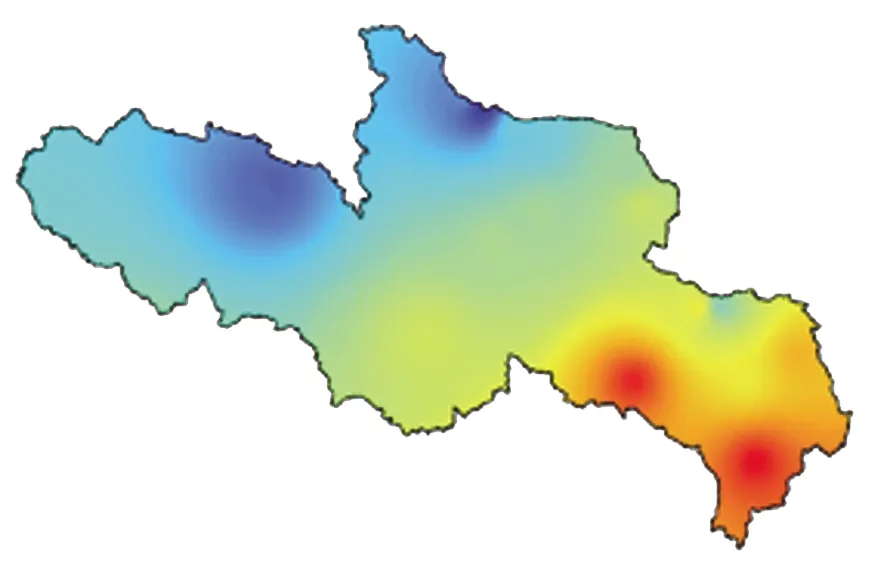
a)IDW

各方法对应年及季节性面平均降水量见表1。其中，春季面平均降水量为93～103 mm，夏季面平均降水量为280～293 mm，秋季面平均降水量为111～119 mm，冬季面平均降水量为12～14 mm，全年面平均降水量为498～521 mm。比较不同插值方法的面平均雨量，不难发现对于全年和各季，普通克里金法和协克里金法对应面平均降水量均大于其他4种方法，且差异较大，其他4种方法差异较小。对比经验信息插值模型和最优信息插值模型2种模型，可发现后者对应面平均降水量在夏季和冬季小于前者，在其他季节大于前者。

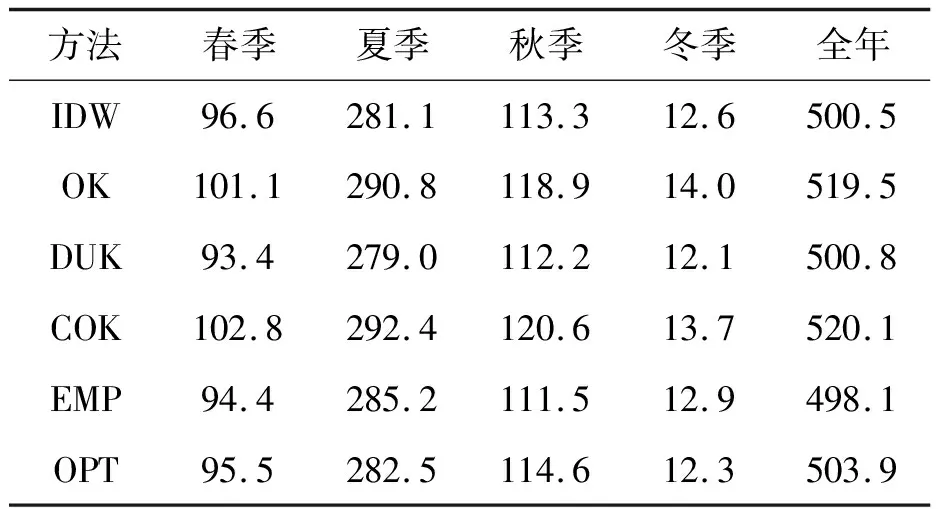
表1 不同插值方法对应流域面平均季节性及年降水量单位：mm

2.2 不同时间尺度插值

为了精确评估信息扩散插值模型的插值精度，研究采用留一交叉验证法对年、季、月及日降水数据进行相应插值研究，并以1.3节中精度指标为依据，对应结果如下。

2.2.1年及季节性降水量

各插值方法对应多年平均年及季节性降水量插值精度见图3。从绝对偏差来看，各方法对于全年和夏季降水量的插值精度最高，ABIAS值约为10%，而后依次是秋季、春季，精度最差的是冬季，ABIAS值达到了28%；全年、春季和秋季降水量对应的相关系数相当，整体在0.85左右，夏季降水量对应的CC值最低，仅为0.71。

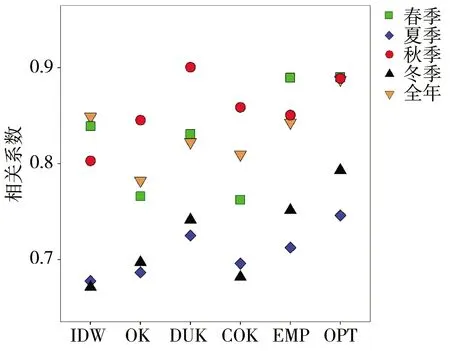
a)相关系数

不同方法对比结果表明，对于全年、春、夏和冬季降水量而言，最优信息插值模型对应插值精度显著优于其他方法，而对于秋季降水量的插值精度也仅次于泛克里金法。经验信息插值模型对应插值精度在绝大多数情况下与泛克里金法相当，普通克里金法与考虑高程因素的协克里金法整体精度相近，但部分季节协克里金法精度甚至要低于普通克里金法，说明考虑高程影响对于分析黄河源区全年及季节性降水空间分布特征的作用较小。反距离加权法的插值精度变幅较大，对于全年、春季和冬季降水量的插值精度尚可，但对于夏季和秋季降水量的插值精度会差于其他方法。

2.2.2月降水量

各插值方法对应多年平均月降水量插值精度见图4。从ABIAS来看，所有方法关于5—10月(降水较大月份)的插值精度会显著大于其他月份，前者的ABIAS处于0.08～0.18范围内，而后者的ABIAS处于0.15～0.45范围内。对比CC结果可发现，7、8、12月对应CC较小，均处于0.55左右；10、11月对应CC较大，均处于0.9左右，其他月份对应CC差异不大，整体处于0.7～0.8范围内。

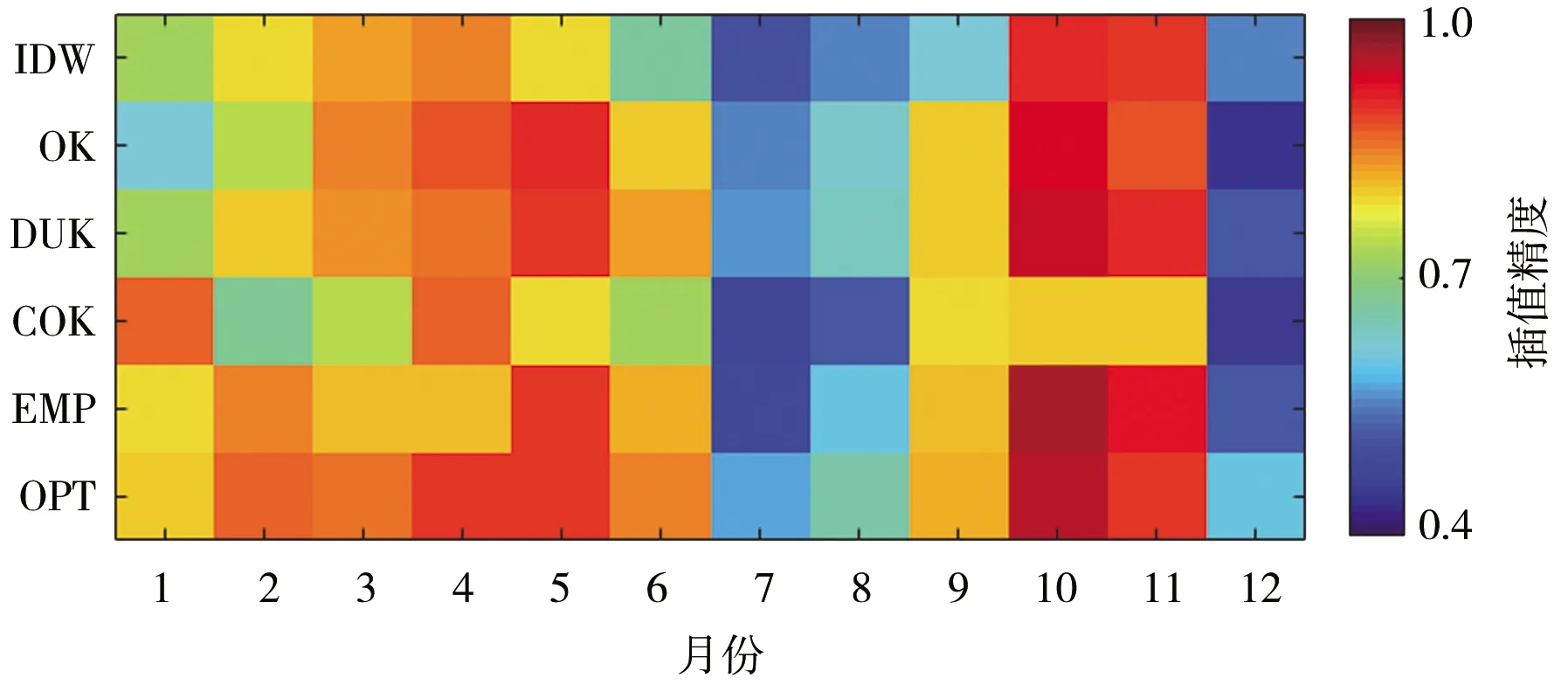
a)CC

不同方法对比结果表明，最优信息插值模型对于绝大多数月份的插值精度会高于其他方法，全年平均 CC为0.80，ABIAS为0.17，RMSE为6.13。经验信息插值模型、普通克里金法和泛克里金法3种方法的插值精度相当，全年平均CC为0.75～0.77，ABIAS为0.18～0.20，RMSE为6.45～6.91；反距离加权法和协克里金法的插值精度略差于其他4种方法，两者全年平均CC分别为0.72和0.71，ABIAS为0.21和0.22，RMSE为8.09和8.88。

2.2.3日降水量

考虑日降水量的年际差异较大，且存在大量“零值”，为尽可能保证日降水数据的特性，本次研究直接将1986年1月1日至2015年12月31日的逐日降水量过程作为实验数据，用于比较不同空间插值方法的精度，具体结果见图5。该图提供了22个站点的不同精度指标分布特性，不难看出，各插值方法对应精度指标均显著差于年、季和月降水量，且不同插值方法间精度差异也不大，这一现象说明了日降水空间插值计算的难度要显著高于年、季和月降水量。

a)CC

不同方法对比结果表明，最优信息插值模型的精度要略优于其他5种方法，22个站点平均CC为0.53，ABIAS为0.95，RMSE为3.21。普通克里金法、泛克里金法、考虑高程因素的协里金法和经验信息插值模型间差异不大，平均CC为0.51～0.52，ABIAS为0.97～0.99，RMSE为3.26～3.30。反距离加权法对应精度略差于其他5种方法，平均CC为0.49，ABIAS为1.00，RMSE为3.38。与年、季和月降水量相似，日降水量的插值结果同样表明，考虑高程因素并不能有效地提高空间插值方法的精度。