变水头入渗条件下VG模型参数变化对土壤入渗的影响
2021-09-08李欣丽
李欣丽,陈 力
(西安理工大学西北旱区生态水利国家重点实验室,陕西 西安 710048)
非饱和土壤水是连接地表水和地下水的纽带,也是农作物和自然植被所需水分的主要来源,研究土壤水分的运动规律可以揭示水文循环的本质,对提高农作物产量、保护生态环境等具有重要意义[1]。目前,有关土壤水分运动的研究手段主要以物理实验和数值模拟为主。随着计算机技术自20世纪80年代起开始普及,数值模拟方法因其操作简便、效率高、受限小、耗时短、适用性广泛等特点被广泛应用于包气带水分运动的研究中,逐渐成为定量分析土壤水分入渗特性的重要手段[2-4]。近年来,国内外学者研发了许多适用于多孔介质中水分运动的数值模拟软件,其中由美国农业部、美国盐碱实验室等机构开发的HYDRUS-1D软件是模拟非饱和土壤水分运动的有力工具之一[5]。HYDRUS-1D模型中采用van Genuchten模型描述土壤水分特征曲线[6-7],其适用范围广且拟合效果较好,但其参数较多且形式较为复杂,并且不同的参数因其物理意义不同对模拟结果有着不同程度的影响,模型参数的准确性会直接影响着模型的精度,因此,模型参数的确定至关重要,而对模型参数进行敏感性分析则有助于参数的率定,从而有利于提高模型的模拟精度。
同时,外部输入条件也是影响模型模拟精度的一个重要因素。目前,有关VG模型参数的敏感性分析研究多集中于定水头入渗条件,如范严伟等[8]研究了van Genuchten模型各参数扰动对不同质地土壤入渗特性的影响;王志涛等[9]研究了定水头入渗条件下van Genuchten模型参数变化对粉壤土入渗特性的影响;高志鹏等[10]分析了HYDRUS模型中土壤水力参数变化对水流和溶质运移变化的敏感性;霍思远等[11]研究发现对于不同的模型输出变量有着不同的参数敏感性。然而,变水头入渗条件更符合实际入渗情况,有关该条件下VG模型参数的敏感性分析较为少见。因此,本研究采用HYDRUS-1D模型模拟土壤一维入渗,以成都市两年一遇设计暴雨过程作为模型上边界条件输入,采用局部分析的方法,对单一模型参数进行敏感性分析,目的在于找出影响土壤入渗特性较为明显的VG模型参数,明确参数敏感性的变化规律,以便于更精准更科学的模拟非饱和土壤水分运动,提高工作效率以及模拟结果的准确性,从而更好地服务实际应用。
1 模型建立
1.1 模型原理
HYDRUS-1D软件采用Richards方程描述一维垂向非饱和土壤中的水分运动[5],其表达式为:
(1)
式中θ——土壤体积含水率,cm3/cm3;t——时间,d;z——垂向坐标,cm;h——土壤水势,cm;K(h)——土壤非饱和导水率,cm/d。
本文采用van Genuchten模型对土壤水分特征曲线和土壤非饱和导水率进行拟合,其方程为[12]:
(2)
(3)
其中,
(4)
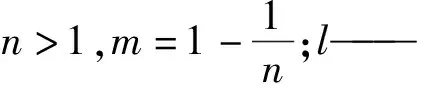
1.2 模型设置
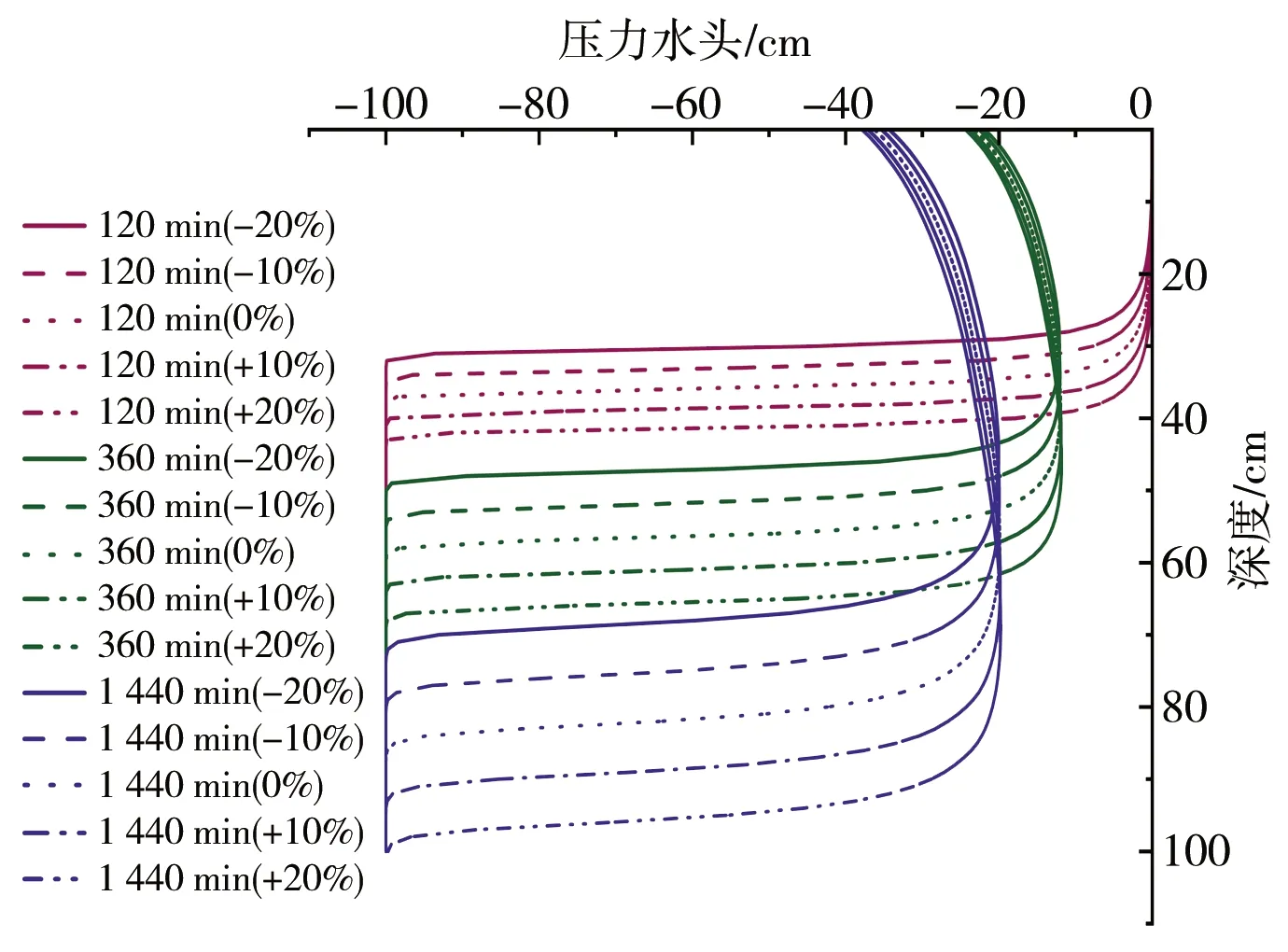
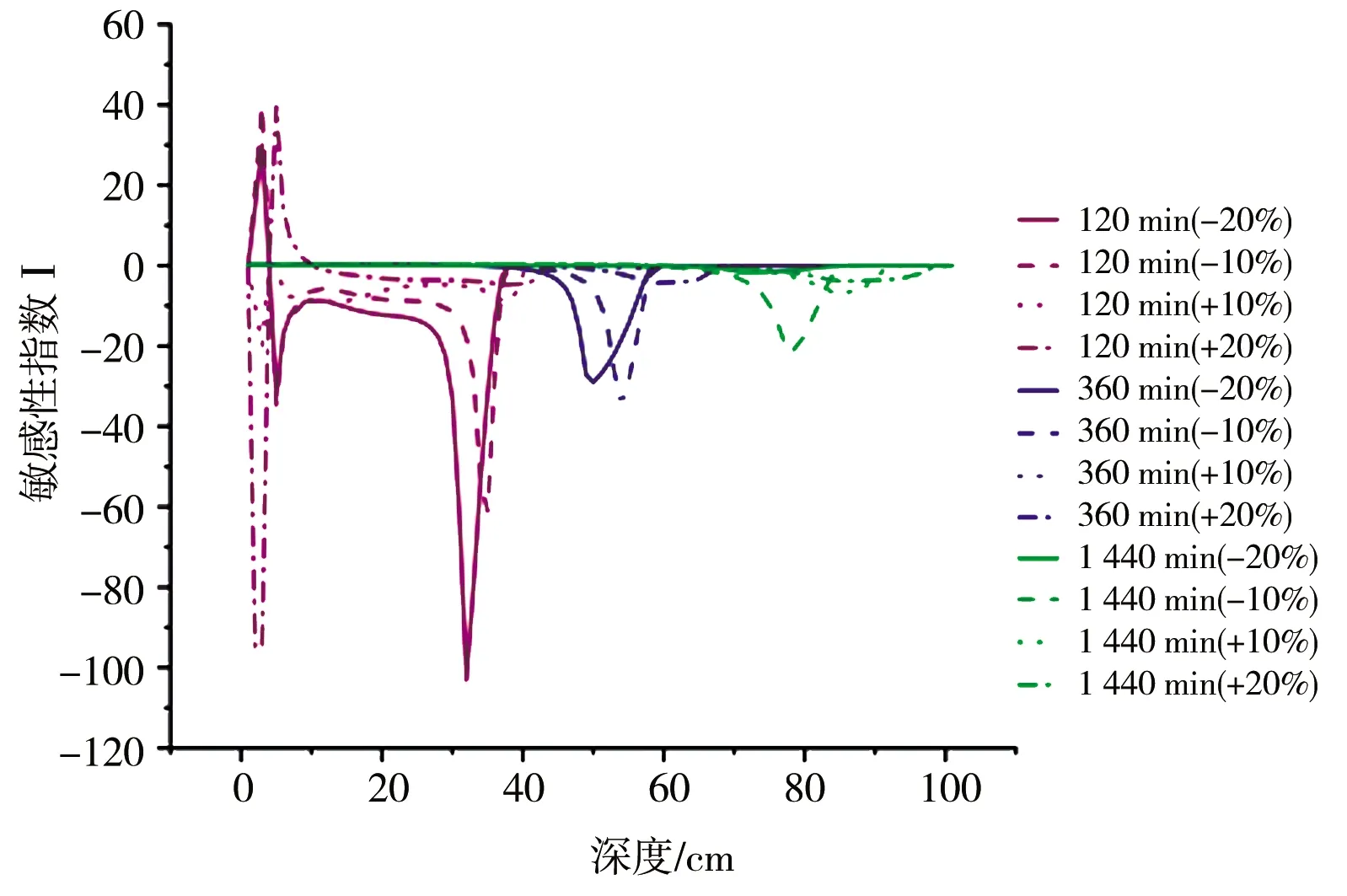
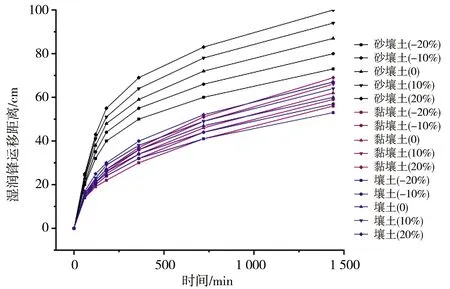
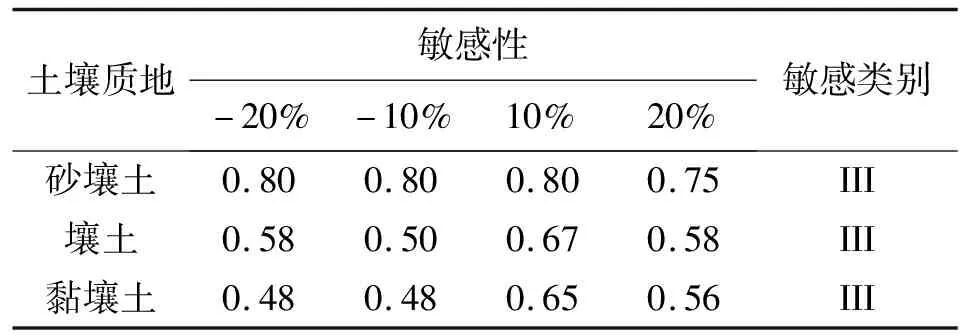
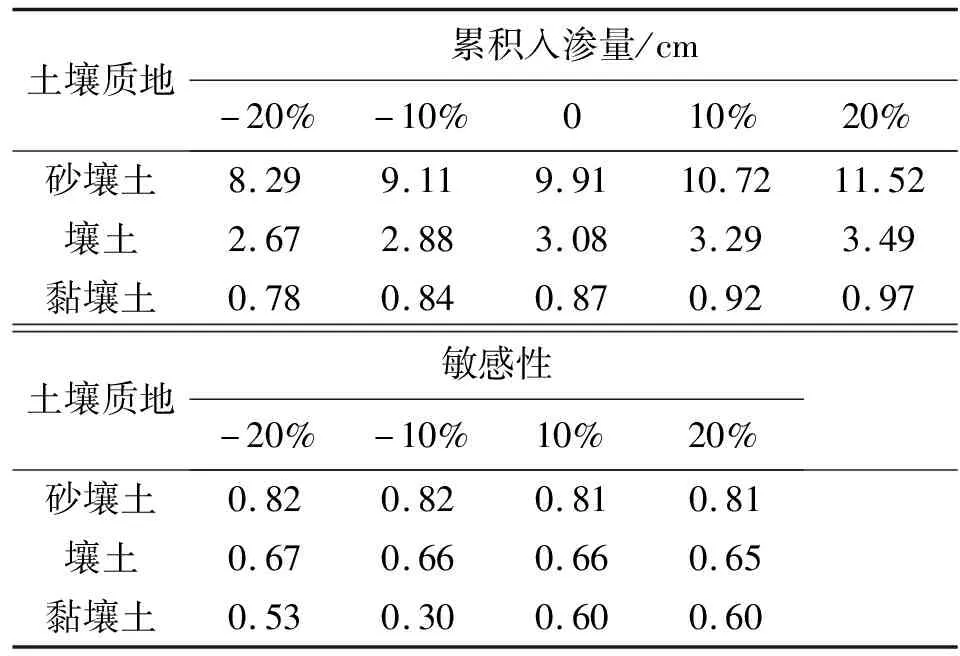
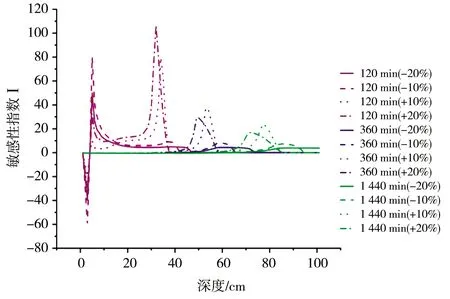
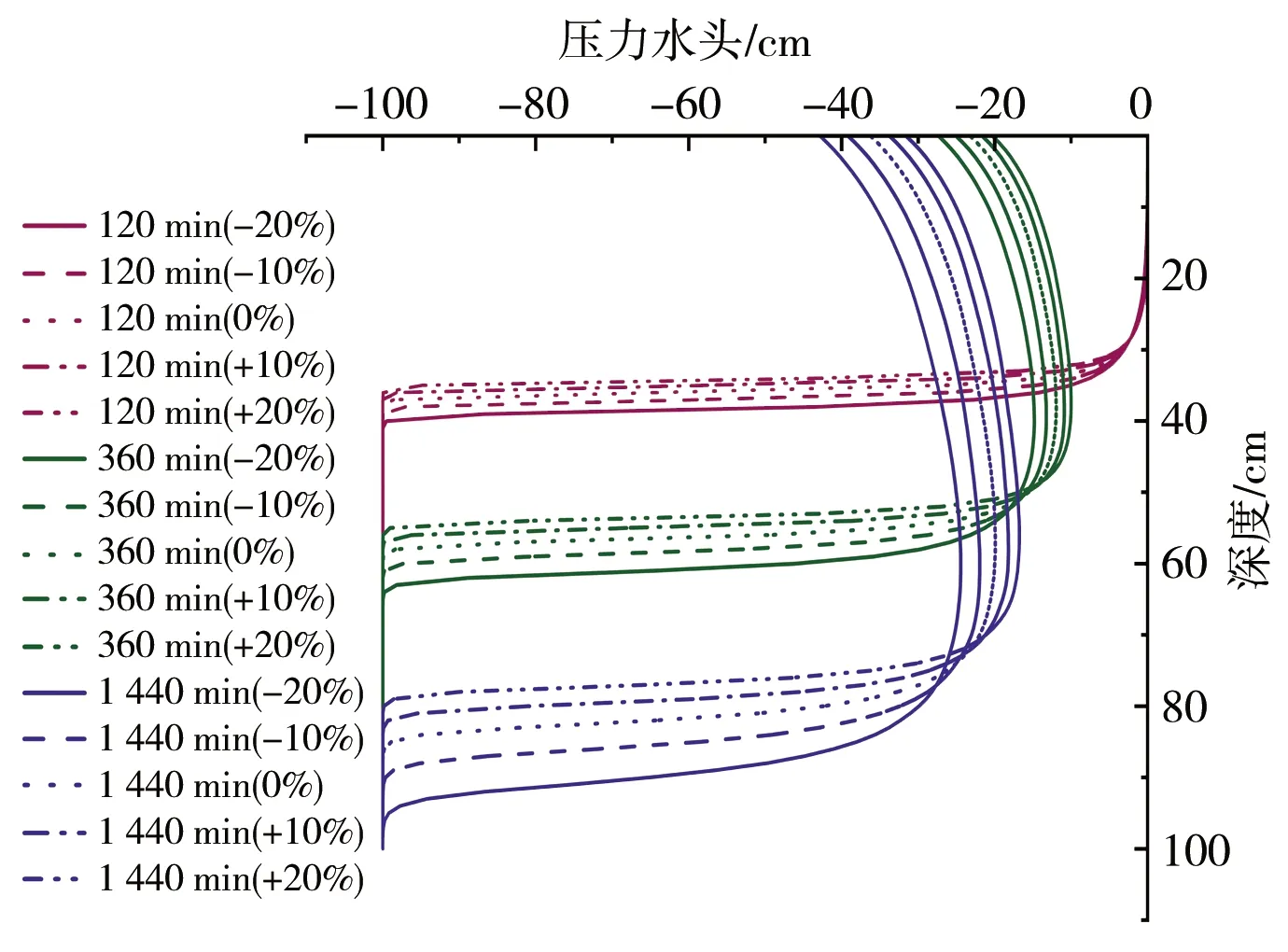
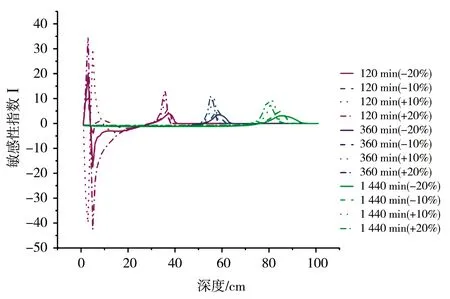
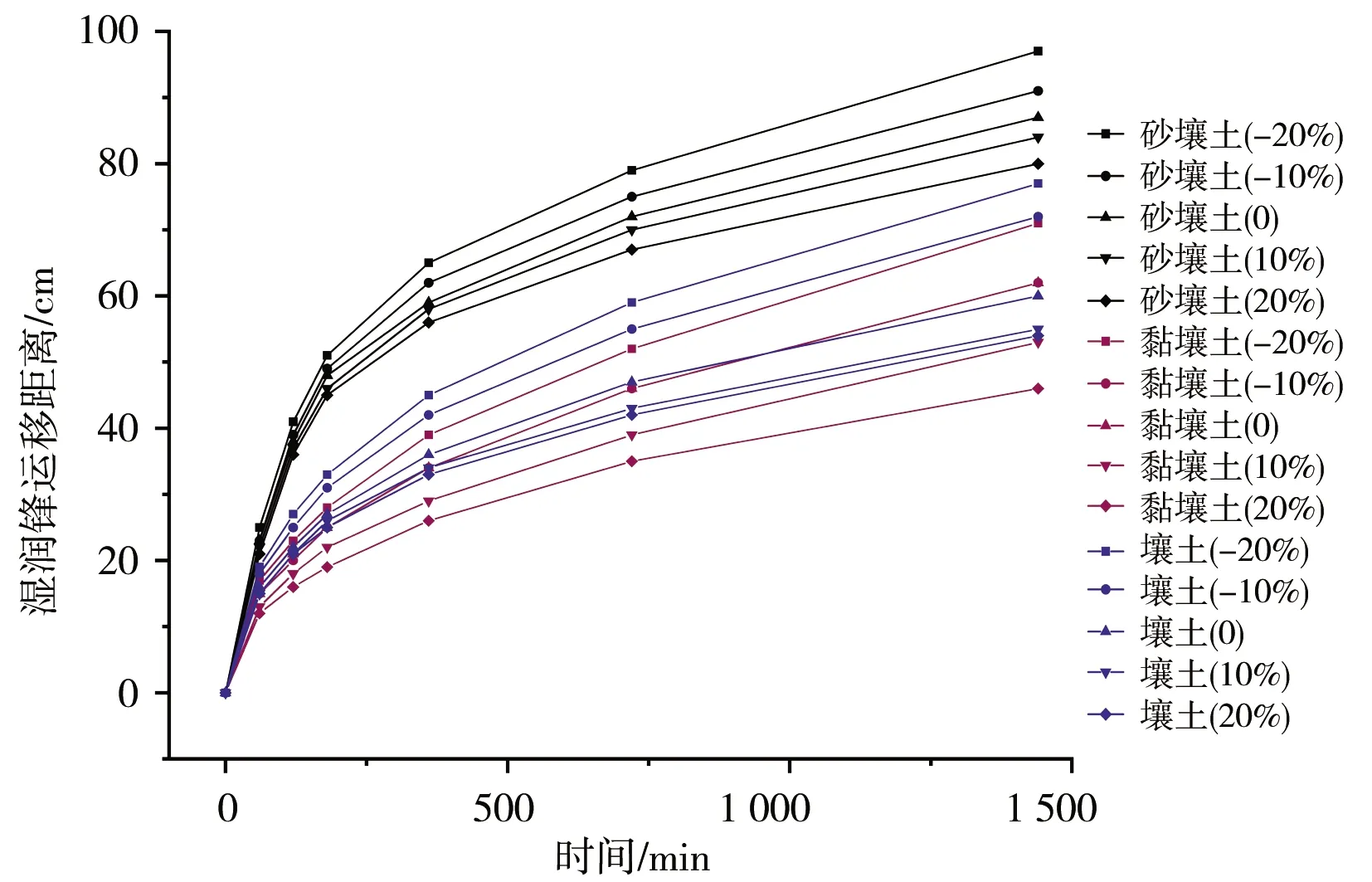
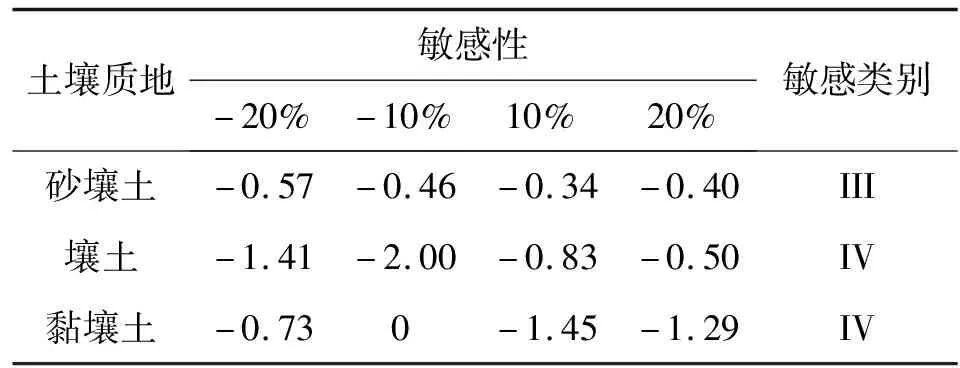
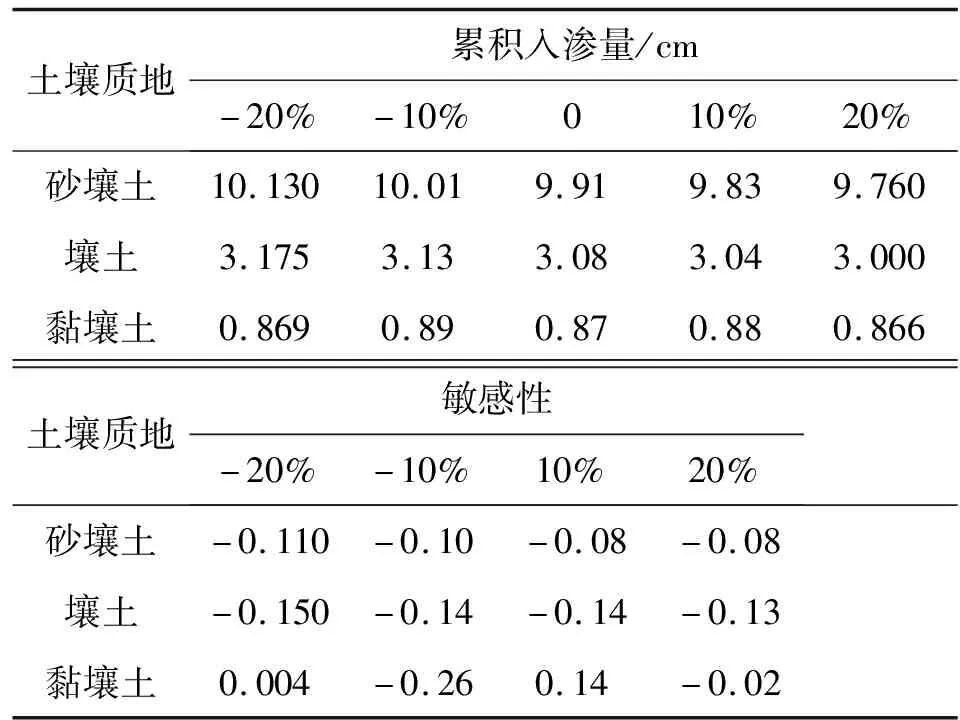
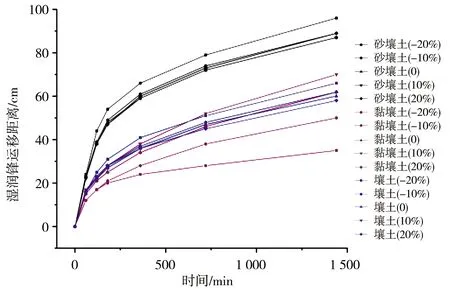
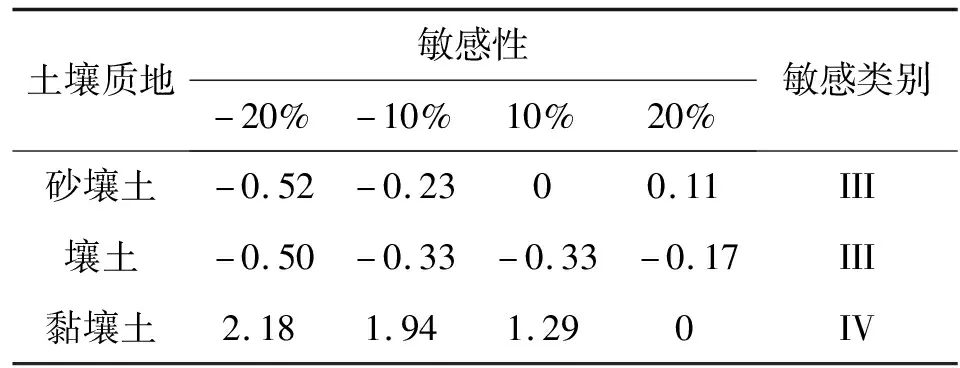
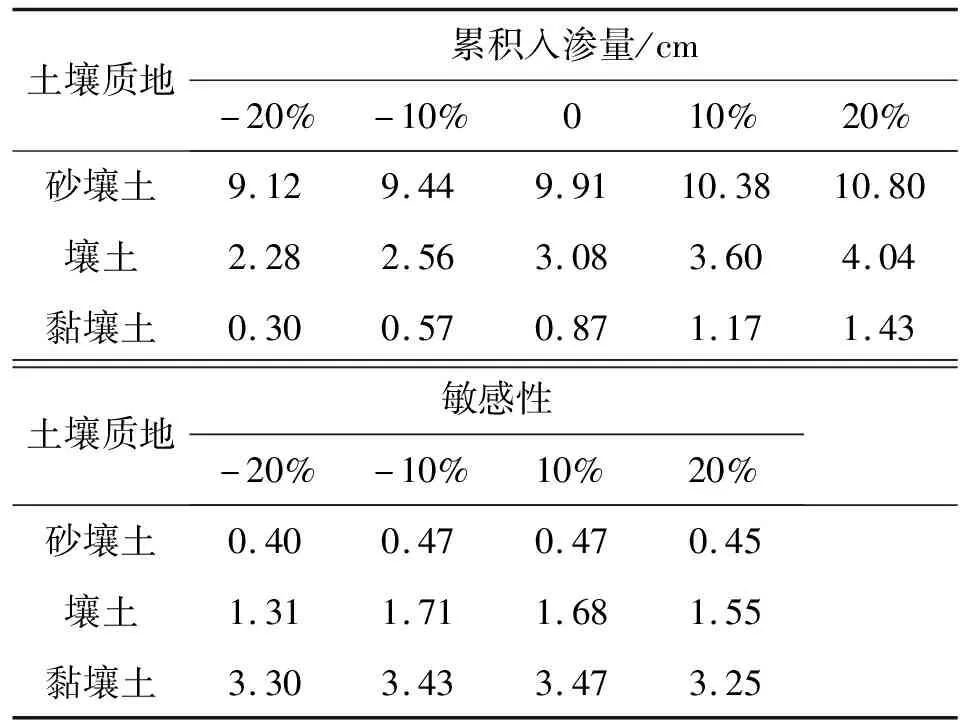
模型模拟0~100 cm深度范围内的均质土壤,土壤类型选用HYDRUS-1D软件中内置砂壤土、壤土以及黏壤土,土壤水流模型选用VG模型,不考虑滞后效应,模拟时长为24 h,上边界为大气降水,下边界为自由排水。芝加哥雨型在国内外短历时暴雨雨型的推求中应用较为广泛[13],其雨型多为单峰雨型。根据赵刘伟等[14]的研究,成都市短历时降雨以单峰型为主,故本文使用成都市新暴雨公式推求成都市区2年一遇设计暴雨量,利用芝加哥雨型推求设计暴雨过程,并作为模型上边界条件进行输入,选取2 h作为降雨历时,给定雨峰相对位置r=0.33(0 (5) 式中i——降雨强度,mm/min;t——降雨历时,min;P——重现期,a。 利用芝加哥雨型所推求的成都市区两年一遇设计暴雨过程见图1。 图1 成都市区两年一遇暴雨过程 选取模型输出变量中的压力水头、湿润锋运移距离、累积入渗量作为研究对象,分析VG模型各参数对输出变量的影响。 局部分析法因其操作简单且高效被广泛应用于模型参数敏感性分析中,故本文采用局部分析的方法对VG模型各个参数进行敏感性分析[15]。模拟时,将其中一个参数进行扰动而不改变其他参数值,重新运行模型,依次得到各情景下的模型输出变量值进行敏感性分析。 本文采用相对敏感值对参数进行归一化处理,计算敏感性指数I[16],进行参数之间的敏感性对比。 (6) 式中O——模型输出结果;Fi——影响模型输出结果的参数值;ΔO——模型输出结果的改变量;ΔFi——参数的改变量。 根据敏感性指数值,对敏感性进行分类,具体见表1。 表1 敏感性分类 VG模型主要包含残余含水量(θr)、饱和导水率(Ks)、饱和含水量(θs)、与进气吸力相关的参数(α)、孔隙尺寸分布指数(n)5个土壤水力参数,本文以HYDRUS-1D软件中提供的砂壤土、壤土、黏壤土的经验参数值为基准,将各参数分别上下扰动10%、20%,得到各情景下的参数取值,参数基准值见表2。根据相关研究[17-18]可知20%内的参数增减变化处于合理范围内。 表2 不同质地土壤VG模型水力参数 图2为Ks扰动下不同质地土壤3个不同时刻(120、360、1 440 min)压力水头随深度的变化规律。从图2可以看出,Ks的扰动对压力水头的影响较大,通过观察同一时刻压力水头曲线之间所围面积,面积越大,其影响越大。随着时间的推移,参数Ks的影响区域逐渐变深。从图3可以看出,Ks扰动对压力水头的影响随土壤质地变细而减小;在降雨过程中,Ks的扰动与壤土、黏壤土压力水头呈正相关,即敏感性指数为负值(由于计算采用负压,故敏感性指数为负时呈正相关),压力水头随Ks增大而增大,降雨结束后,Ks与土壤表层10 cm内压力水头呈负相关,而与其他深度呈正相关。该结论与定水头入渗条件下研究结论并不相同,如高志鹏等[10]研究表明Ks的扰动对压力水头的影响呈非线性正相关,其原因可能是定水头入渗条件下研究水分入渗贯穿整个模拟期且其敏感指数采用平均值,而本文中降雨历时仅为2 h且其敏感性受降雨影响较大。同一质地土壤的Ks敏感性在降雨结束时达到最大,之后随时间增加而减小,且不同时刻所影响的土壤深度范围也不同,随湿润锋运移而不断变化,例如T=120 min时,Ks对砂壤土的影响范围为0~40 cm,而T=360 min时,Ks对砂壤土的影响范围为40~60 cm。Ks的敏感性随土壤质地变细而减小,Ks的扰动对砂壤土的影响最大,其敏感性指数最高可达-103,并且影响范围为整个土壤剖面。 a)砂壤土 a)砂壤土 Ks扰动下湿润锋运移距离随时间的变化规律曲线见图4。计算T=1 440 min时刻各质地土壤湿润锋运移距离在Ks不同扰动下的敏感指数值,见表3(敏感类别按照参数对输出变量影响最大的敏感性指数绝对值进行排序)。 图4 Ks扰动下不同质地土壤湿润锋运移距离的变化规律 表3 Ks扰动对不同质地土壤湿润锋运移距离的影响 由图4、表3参数的敏感指数可知,随着时间的推移,湿润锋逐渐向深处推进,其增加速度呈先快后慢的趋势,且增速在降雨结束后逐渐减缓。砂壤土在Ks扰动下的湿润锋运移距离最远,黏壤土次之,壤土最浅。Ks扰动对湿润锋运移距离影响较大,Ks的扰动与湿润锋运移距离呈正相关,且其敏感性随土壤质地变细而减小。Ks的正负扰动对砂壤土的湿润锋运移距离影响程度基本相同,而对于壤土和黏壤土来说,Ks的正扰动影响程度略大于负扰动。Ks与土壤渗透性能有关,质地较粗的土壤Ks较大,渗透能力较强,故湿润锋运移距离远,由于其孔隙较大且排列较为疏松,故Ks扰动对粗质地土壤的影响较大。 由表4可知,3种质地壤敏感类别都为III,且Ks的扰动与累积入渗量呈正相关关系,且Ks的敏感性随土壤质地变细而减小。Ks的扰动对3个输出变量都具有较大影响,且其影响程度均随土壤质地变细而减小。Ks空间变异显著,可由实验测定,但应考虑其尺度效应。有相关研究[19]表明,Ks可根据土壤理化参数(土壤质地、粒径分析等)建立土壤转换函数,估测其空间分布。 表4 Ks扰动对不同质地土壤累积入渗量的影响 θr的扰动对压力水头的影响规律与Ks相似,但影响程度远小于Ks。以壤土为例(图5),降雨结束时,θr扰动的影响范围为0~20 cm,并且其最大敏感指数值仅为-2.65(图6),而同情况下Ks扰动的敏感指数可达14.12。与其他参数相比,θr的扰动对压力水头的影响较小,并且θr对压力水头的影响程度于同一时刻呈先增加后减少的趋势。 a)砂壤土 a)砂壤土 由图7、表5参数的敏感指数可知,在θr扰动下,土壤质地越粗,湿润锋运移距离越远;θr的扰动对砂壤土的湿润锋入渗深度影响较小,且其影响随土壤质地由粗至细逐渐增加。θr对VG模型低含水率段影响显著,质地较细的土壤有着较高的θr,其持水能力强,孔隙较细且连通性较差,故θr扰动对细质地土壤的影响较大。 图7 θr扰动下不同质地土壤湿润锋运移距离的变化规律 表5 θr扰动对不同质地土壤湿润锋运移距离的影响 由表6可知,3种质地土壤的敏感类别分别为I、II、III,且θr的扰动对砂壤土、壤土的累积入渗量影响甚微,其敏感性指数值均低于±0.1,可忽略不计;而对于黏壤土来说,在θr扰动为-20%时,也仅为-0.21,影响较小;θr的敏感性随土壤质地变细而增加,但与其他参数相比,其影响很小。累积入渗量一般与初始含水量有关,而与θr关系较小。总的来看,θr的扰动对不同输出变量的影响规律不同,但影响程度均较低。由于实际残余含水量θr的获取较为困难,在θr未确定时,可将压头为-15 000 cm时所对应的含水量作为θr的初估值[12]。 表6 θr扰动对不同质地土壤累积入渗量的影响 由图8、9可知,θs的变化对压力水头的影响较大,其敏感性随土壤质地变细而减小,并且θs的正扰动对压力水头的影响大于负扰动。以砂壤土为例,T=120 min时,+20%扰动情景下θs的最大敏感指数为106.5,是-20%扰动的2.13倍。降雨过程中,θs的扰动与壤土、黏壤土压力水头呈负相关,降雨结束后,θs与土壤表层20 cm内压力水头呈正相关。该结论与定水头入渗条件下研究结论并不相同,如高志鹏等[10]研究表明θs的扰动对压力水头的影响呈非线性负相关,定水头入渗会使得表层土壤在短时间内达到饱和,其水分入渗贯穿整个模拟期且敏感指数采用平均值,而本文中降雨历时仅为2 h且其敏感性受降雨影响较大。 a)砂壤土 a)砂壤土 由图10和表7参数的敏感指数可知,θs扰动对湿润锋运移距离的影响较大,θs的扰动与砂壤土、壤土湿润锋运移距离呈负相关,且其负扰动影响大于正扰动。湿润锋运移距离在θs扰动下随土壤质地变细而减小。由表8可知,3种质地土壤的敏感类别分别为II、III、III,且θs的扰动与累积入渗量呈正相关,且其敏感性随土壤质地由粗到细逐渐增加。对于砂壤土和壤土来说,θs的正负扰动对累积入渗量影响程度基本相同。θs越小,越易饱和,湿润锋运移距离越远,累积入渗量越大,而粗质地土壤饱和导水率大,其孔隙较大且排列较为疏松,更易入渗,故θs在同扰动情况下对细质地土壤累积入渗量的影响更大。θs扰动对3个输出变量的影响规律不同,但影响程度均较大。实际上,θs可通过实验准确获得,故应尽可能取实测值以减少误差。 图10 θs扰动下不同质地土壤湿润锋运移距离的变化规律 表7 θs扰动对不同质地土壤湿润锋运移距离的影响 表8 θs扰动对不同质地土壤累积入渗量的影响 由图11、12可知,α对地表0~20 cm附近压力水头的敏感性较高,且其敏感性随土壤质地变细而减小;α的影响区域随时间推移而逐渐扩大,以壤土为例,T=120 min时,α的影响范围为0~20 cm,而T=360 min时,其影响范围增至0~40 cm。 a)砂壤土 a)砂壤土 由图13及表9可知,α的负扰动越大,湿润锋的运移距离越深;α的扰动对壤土、黏壤土湿润锋入渗深度的影响较大,敏感类别为IV;α是对壤土湿润锋运移影响最大的参数。由表10可知,3种质地土壤的敏感类别分别为II、II、III,且α的变化对累积入渗量的影响较小,其敏感指数范围仅为-0.26~0.14,影响程度比θr略高。α一般被认为进气吸力的倒数,粗质地土壤进气吸力较小,更易排水,其α值更大,故α在相同扰动情况下对粗质地土壤湿润锋运移的影响较小。累积入渗量一般与初始含水量及饱和含水量有关,与α关联较小。α的扰动对湿润锋运移距离影响较大,对压力水头和累积入渗量影响较小,但略大于θr。α是与进气值和孔径分布相关的参数,通常经由土壤水分特征曲线多次迭代拟合确定,有研究[20]表明,利用简单入渗法直接推求VG模型参数α具有较高的测定精度,但需保证吸渗率的准确度。 图13 α扰动下不同质地土壤湿润锋运移距离的变化规律 表9 α扰动对不同质地土壤湿润锋运移距离的影响 表10 α扰动对不同质地土壤累积入渗量的影响 由图14、15可以看出,降雨结束时,n的扰动对0~10 cm土壤层压力水头的影响最大,以砂壤土为例,其最大敏感性指数值可达-350;并且n扰动的影响范围随土壤质地变细逐渐减小,n的扰动对压力水头的影响规律与θs相似,但其影响程度大于θs,其敏感性随土壤质地变细而减小。以壤土为例,-10%扰动下n的最大敏感值为75.3,是同情况下θs的12.86倍。降雨结束之后,n的扰动对3种质地土壤压力水头的影响较小,均不超过±3.5。 a)砂壤土 a)砂壤土 由图16及表11可知,n负扰动对湿润锋运移距离的影响大于正扰动,n扰动对细质地土壤影响较大。n扰动与壤土的湿润锋运移距离呈负相关,该结论与定水头入渗条件下研究结论并不相同,如范严伟等[8]研究发现n扰动与湿润锋运移距离呈正相关关系,其原因可能是定水头入渗条件下供水速率均匀,入渗取决于土壤渗透能力,而变水头入渗条件供水速率不恒定,入渗取决于供水速率或者土壤渗透能力,且n不确定性强,易受土壤结构、质地等因素以及外部条件的影响。由表12可知,3种质地土壤的敏感类别分别为III、IV、IV,且n的扰动与累积入渗量呈正相关关系,其敏感性随土壤质地变细而显著增加,质地较细的土壤n较小,其结合水能力较强,水分不易排出,在n扰动相同的情况下,细质地土壤累积入渗量所受到的影响较大,n的正负扰动对累积入渗量的影响程度基本相同;相比于其他参数,n是对壤土、黏壤土累积入渗量影响最大的参数。总之,n扰动对3个输出变量都具有较大影响,其确定与参数α类似。 图16 n扰动下不同质地土壤湿润锋运移距离的变化规律 表11 n扰动对不同质地土壤湿润锋运移距离的影响 表12 n扰动对不同质地土壤累积入渗量的影响 结合前人研究[8-9,21]对比,边界条件不同也会导致参数敏感性的改变。变水头入渗条件与定水头入渗对模型输出结果的影响存在差异,定水头入渗条件下的累积入渗量大于变水头入渗,而湿润锋运移距离则小于后者。入渗水头对入渗系数有着较大的影响[22],定水头入渗条件下入渗水头不变,入渗主要取决于土壤渗透条件,而变水头入渗条件下入渗水头随时间变化,入渗取决于土壤渗透条件与供水条件两者的相互作用。对于输出变量湿润锋运移距离来说,定水头入渗条件下参数θr、Ks的敏感性大小与变水头入渗基本相同,参数θs、α敏感性小于变水头入渗,而参数n大于变水头入渗;对于累积入渗量来说,定水头入渗条件下参数Ks的敏感性大小与变水头入渗基本相同,参数θr、θs、α大于变水头入渗,而参数n小于变水头入渗。 土壤质地对不同输出结果参数敏感性有着一定的影响[23-24],土壤的持水能力与孔隙大小及其分布状况有关,细质地的土壤有着较高的θr和θs,持水能力较强,孔隙较细且连通透性较差,湿润锋运移距离较小,累积入渗量较小,故在θs扰动下,细质地土壤所受影响较大;粗质地土壤Ks较大,渗透能力强,在Ks扰动下,粗质地土壤所受影响较大;土壤质地与α、n存在某种联系,土壤质地越粗,α、n越大,在相同的α、n扰动下,细质地土壤湿润锋运移距离的变化更大;累积入渗量一般与初始含水量及θs有关,与θr、α、n关联较小,故参数敏感性也较小。 VG模型参数应依据自身物理意义进行确定。不同质地土壤条件下的θr数值较小,且变化范围较小,具有较强的确定性,并且θr对输出变量的影响均较小,故可采用PTFs法进行推测或者使用压头为-15 000 cm时所对应的含水量;θs的变化范围较小,确定性较强,实验测定的θs值较为准确,故实际应用时尽量选取实测值;α、n具有很强的不确定性,随土壤质地和结构不同而变化,土壤持水能力随α增加而减小,有研究[25]表明,α不仅与进气吸力有关,与n也存在非线性关系,只有在土壤质地较粗时,1/α与进气值近似相等,细质地土壤的1/α均大于进气值;n的取值影响着土壤水分特征曲线的形状,并与土壤孔隙大小分布有关,采用土壤水分特征曲线多次迭代拟合确定;Ks变化范围较大,不确定性强,空间变异性较大,Ks可由试验测定,但应根据所选研究对象选择适合的方法,例如,采用变水头法测定较细土壤的Ks较为合适,并可基于实测值结合土壤水分运动数据进一步优化拟合,以提高估计效率,减小不确定性。除此之外,也可根据土壤理化参数建立土壤转换函数,估算Ks空间分布。 变水头入渗条件下,不同质地土壤VG模型各参数对模型输出结果的敏感性具有以下规律。 a)VG模型各参数对压力水头的影响均随土壤质地变细而减小,并且影响区域随时间增加逐渐变深。同质地土壤各参数敏感性在降雨结束时达到最大,之后随时间增加而减小。各参数敏感性排序为:n>θs>Ks>α>θr(砂壤土、壤土);n>θs>Ks>θr>α(黏壤土)。其中,n、Ks、θs是对压力水头影响较大的参数。 b)VG模型各参数对不同质地土壤湿润锋运移距离的影响具有较大差异,各参数敏感性排序为:θs>Ks>α>n>θr(砂壤土);α>θs>Ks>θr>n(壤土);n>α>θr>θs>Ks(黏壤土)。 c)同一参数的正负扰动对累积入渗量的影响程度基本相同,各参数敏感性排序为:Ks>n>θs>α>θr(砂壤土);n>Ks>θs>α>θr(壤土);n>θs>Ks>α>θr(黏壤土)。其中,n、Ks、θs是对累积入渗量影响较大的参数,并且其扰动与累积入渗量呈正相关关系。 d)边界条件的不同也会导致参数敏感性发生改变,变水头入渗下VG模型各参数对模型输出结果的敏感性与定水头入渗不同,故进行模拟时应确保边界条件的真实性。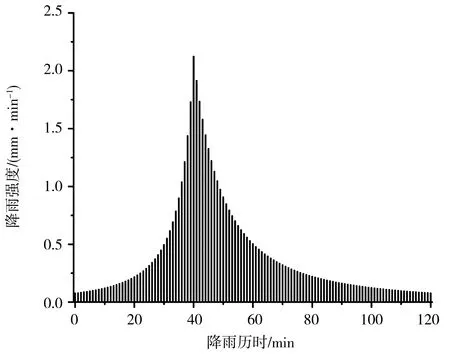
1.3 输出变量选取
2 参数敏感性分析
2.1 参数敏感性分析理论依据

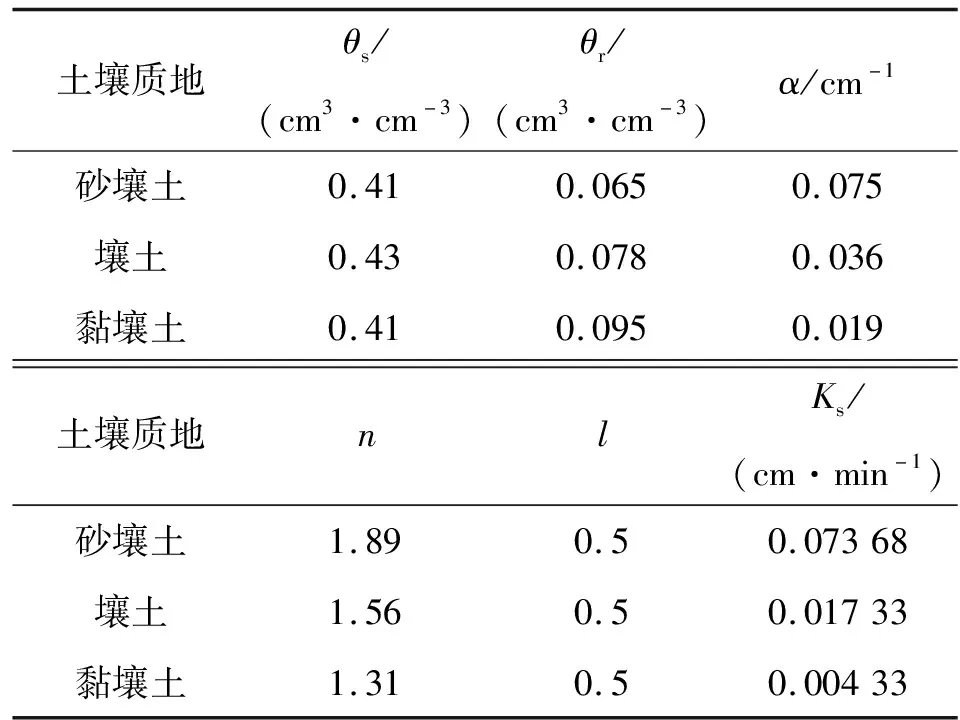
2.2 参数取值
3 结果与分析
3.1 Ks敏感性分析
3.2 θr敏感性分析
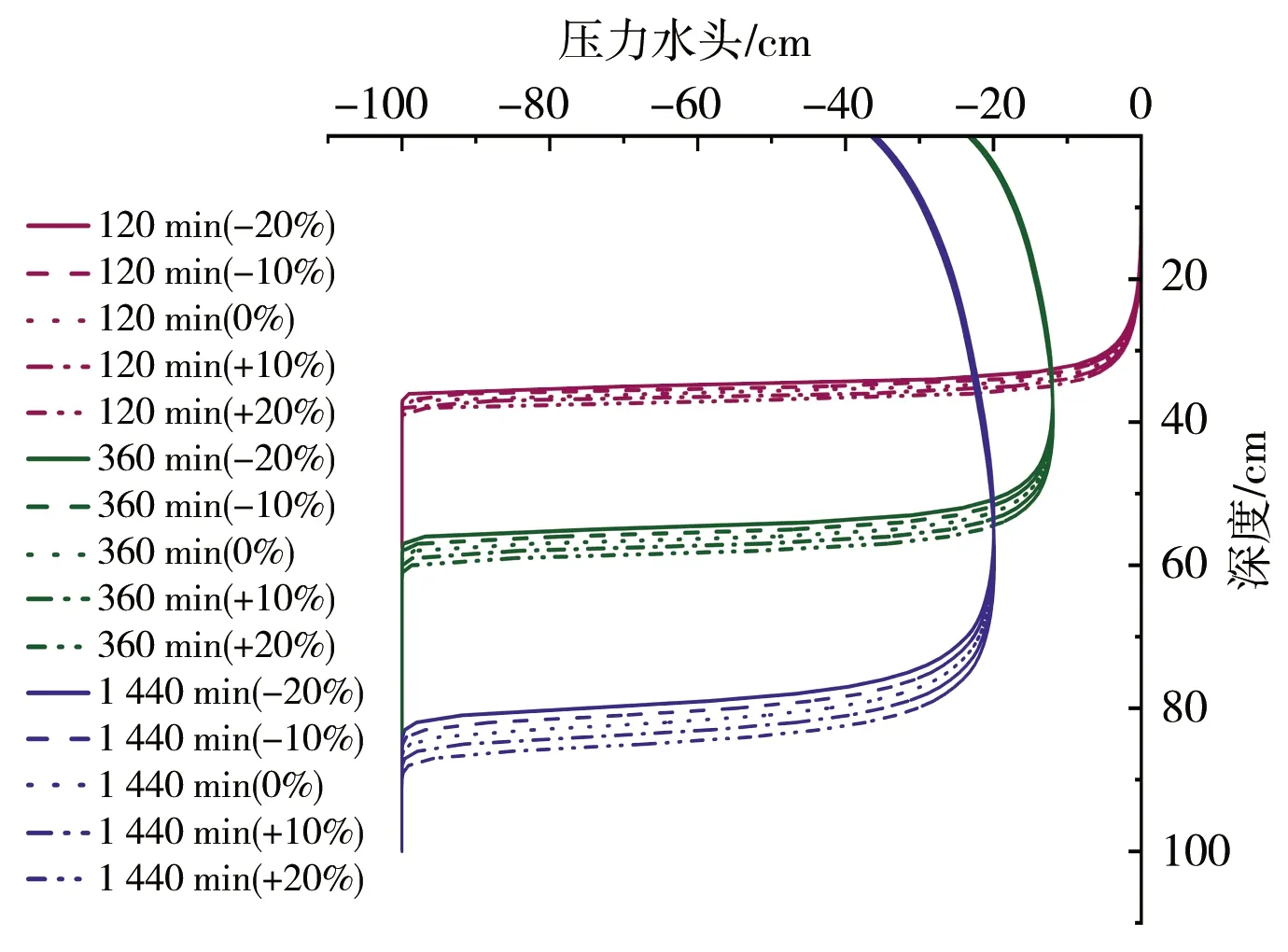
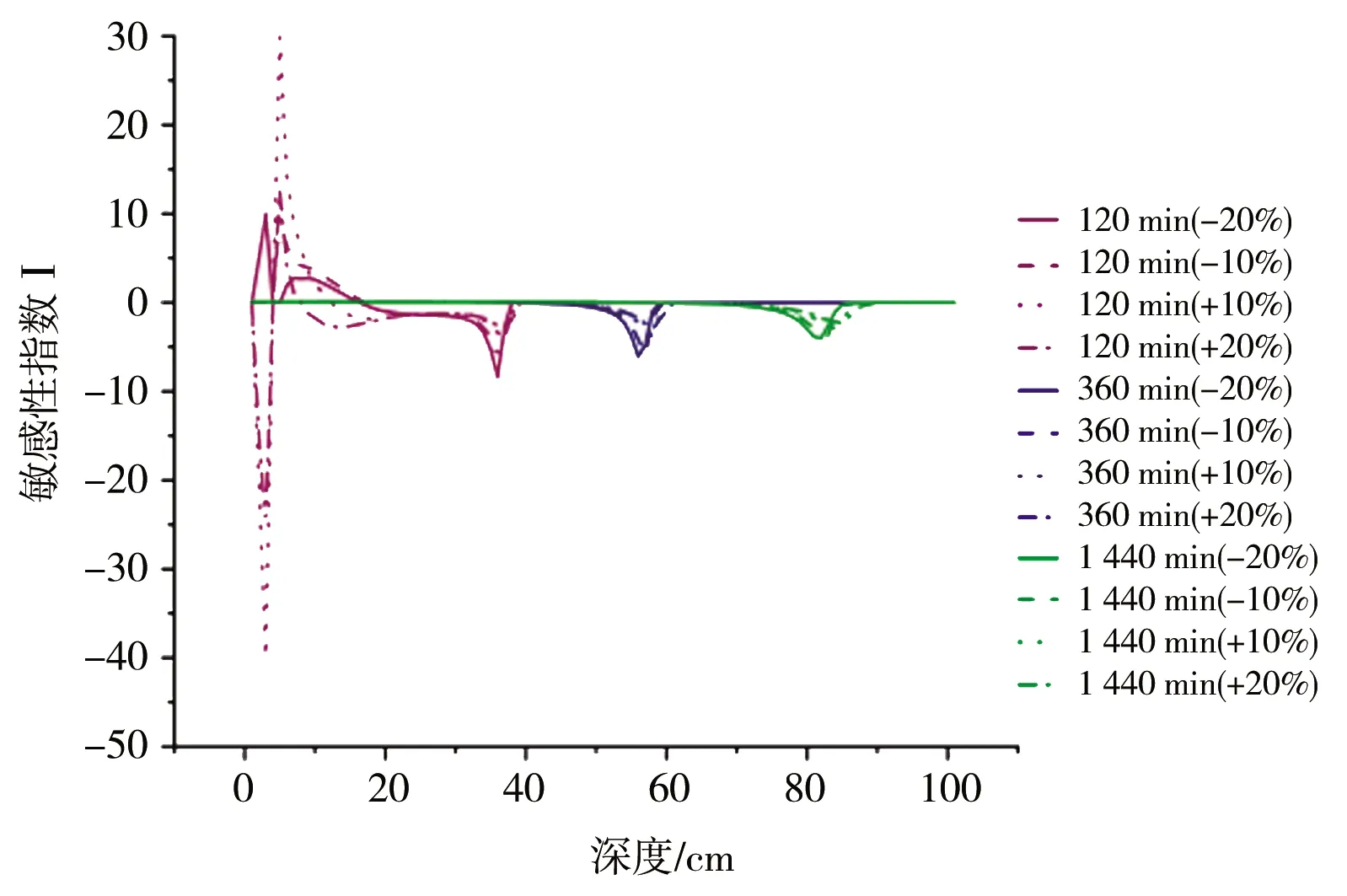

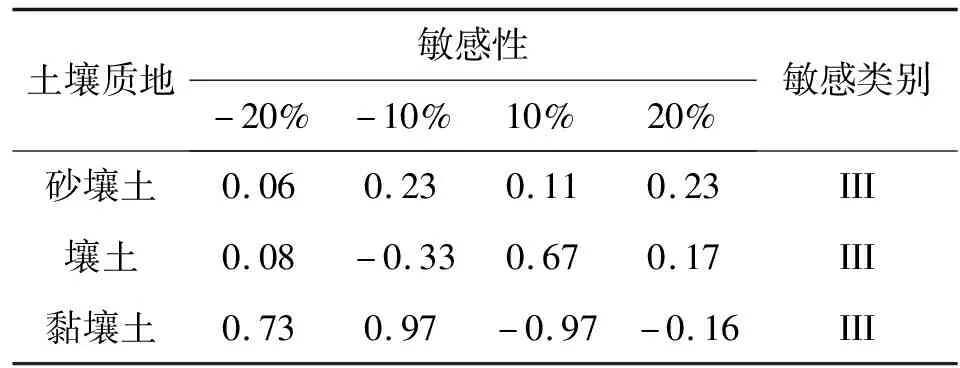

3.3 θs敏感性分析
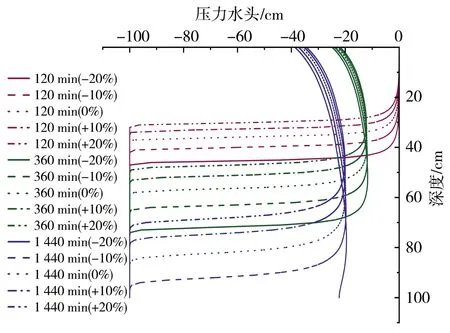


3.4 α敏感性分析
3.5 n敏感性分析


4 讨论
5 结论
