RNN与LSTM方法用于滑坡位移动态预测的研究

张明岳，李丽敏，温宗周

(西安工程大学电子信息学院，陕西 西安 710600)

滑坡灾害严重威胁着国家生态环境和当地居民的人身安全，滑坡监测的预警、预报因可以有效避免灾害造成的各方面损失而显得尤为重要。目前，滑坡预测研究主要分为时间、空间2种预测方法[1]。在滑坡区域确定的前提下，如何更加准确地预测在不同时间滑坡的位移成为关键问题。例如雷德鑫等[2]基于时间序列分析，采用差分整合移动平均自回归(Auto Regressive Integrated Moving Average,ARIMA)模型预测滑坡位移，实现对滑坡位移滚动预测，但由于滑坡非线性动力学特征复杂致使预测时间延长、预测精度下降，可见滑坡位移的演化是呈动态的。杨背背等[3]基于时间序列的滑坡位移动态预测模型在实际应用中预测结果较好，但其预测精度和计算时间明显受制于算法结构，可见算法本身参数数量和结构复杂程度也影响着预测精度。

从以往的滑坡位移研究成果来看，多数研究人员使用径向基函数(Radial Basis Function,RBF)、反向传播(Back Propagation,BP)、K-means等智能算法，然而这些算法从实际应用的情况来看还存在如下问题：①RBF神经网络具有较强的聚类能力，在处理复杂事物和大量数据方面能力较强，但其是一个静态网络，不能用于滑坡动态预测；②BP神经网络可以解决非线性问题，但由于其网络自身的局限性，在训练过程中会出现陷入局部极小值、收敛速度慢等问题[4]，对训练样本具有依赖性。

循环神经网络RNN主要用于对时序数据的处理和预测，是一种典型的动态神经网络。其具有以下优势：①适用于时序数据的处理，拥有记忆功能，使得前一时刻的状态能够对后一时刻的状态造成影响，实现网络状态的反馈；②在LSTM中，引入“门”解决了神经网络中长序列依赖问题；③RNN本身特有的结构使其预测精度更加准确。RNN的提出是为了描述一个序列当前的输出与之前状态信息的关系。RNN包括以下3个特性：①RNN隐含层神经单元间的连接是循环的；②RNN能够在每个时间节点产生一个输出向量值，且该时间节点上的输出值仅与下一时间节点的隐单元有循环连接；③RNN能够处理序列数据并输出单一的预测，即RNN会记忆之前的信息，并利用之前的信息作用于后面结点的输出。RNN相较于传统神经网络的隐藏层各结点间是有连接的，隐藏层的输入不仅包括输入层的输出，还包括上一时刻隐藏层的输出[5]。

LSTM是一种特定形式的RNN，它的提出是为了解决RNN在处理长期依赖时产生的梯度爆炸或梯度消失的现象，其在其他领域也取得了惊人的成就。例如朱肖颖等[6]应用LSTM模型进行新闻分类，在对原始数据展开格式变换、分词加工后，进行特征提取并建立LSTM网络模型，解决在海量新闻数据下RNN存在的梯度消失现象已不能提高分类效率的问题，表现出LSTM模型的高准确度和良好的扩展性；王森等[7]通过时间序列模型LSTM对故障的燃料电池进行分类，试验结果表明分类准确率高达到95%以上；权波等[8]基于LSTM的船舶航迹预测模型，以广州港内的船舶AIS数据作为LSTM模型的输入矢量进行训练，并对未来船舶航行轨迹进行预测，突显出LSTM模型预测法具有高精确度；陈超强等[9]提出了自动编码器和LSTM相结合的步态预测模型，该模型可以根据前一时刻的步态序列预测出下一时刻的步态信息，解决了下肢外骨骼机器人跟随控制问题。结果表明，该模型平均预测准确率能够达到92.9%以上。可见LSTM在诸多领域应用中具有一定的优势，但在滑坡预测领域涉及较少，因此其具有较好的研究前景。

LSTM与RNN同属于动态神经网络，2种算法均可用于时序数据的处理，并且在处理长序列数据预测问题方面具有明显的优势，但在滑坡位移预测方面的应用较少。因此，本文分别使用LSTM和RNN 2种算法，通过对监测点数据采用“3δ”法及归一化处理并建立动态模型，应用于新滩滑坡工程中。最后，将2种预测模型得到的实验结果与实测数据进行比对得出预测精度，并利用MAE与MAPE 2个指标做出评价。

1 RNN与LSTM基本原理

1.1 RNN与LSTM描述

1.1.1RNN算法描述

图1为循环神经网络RNN结构。该网络分为3层：输入层、隐藏层、输出层[10]。其中x为输入层的向量值，s为隐藏层的向量值[11](由当前输入向量x与隐含层上一次的值st-1共同决定)，o为输出层的向量值。U为连接输入层到隐含层的权重矩阵，W为隐藏层的权重矩阵(取决于隐藏层上一时刻的值)，V是隐藏层到输出层的权重矩阵[12]。

图1 RNN网络结构

式(1)、(2)为循环神经网络计算方法：

st=f(UXt+Wst-1)

(1)

ot=g(Vst)

(2)

式(1)表示隐藏层的计算过程，其中f为激活函数，U代表输入向量值x的权重矩阵，W为上一时刻结果作为本次输入时的权重矩阵。式(2)表示t时刻输出层向量值ot的计算过程，输出层的每个节点都和隐藏层的对应节点相连。Vst为输出层的权重矩阵，g为激活函数。RNN采用BPTT算法进行训练。

1.1.2LSTM算法描述

理论上，RNN能够处理任意长的序列。然而在实际应用中，RNN会出现梯度消失问题。为了克服传统RNN的缺点，提出了一种特殊的RNN，称为LSTM神经网络。与传统RNN相比，LSTM中隐藏层的基本单元是存储块。存储块包含内存单元和3个“门”(遗忘门、输入门、输出门)。通过这3个“门”调节信息流入和流出存储单元。输入门控制进入存储单元的输入向量。遗忘门控制上一时间步骤中的信息是被记住还是被遗忘。当遗忘门打开时，上一时刻的信息传递到下一时刻；当遗忘门关闭时，上一时刻的所有信息都被遗忘，不能传递到下一时刻。这意味着遗忘门可以过滤信息，保留有用的信息，丢弃无用的信息。输出门控制输出向量到其他块或最终结果。图2为RNN与LSTM结构对比。

a)RNN

RNN与LSTM的关键区别在于隐向量的构造。LSTM的主要结构算法:

ft=σ(Wf·[ht-1,xt]+bf)

(3)

it=σ(Wi·[ht-1,xt]+bi)

(4)

(5)

(6)

ot=σ(Wo·[ht-1,xt]+bo)

(7)

ht=ot·tanh(ct)

(8)

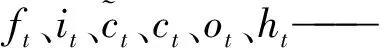
LSTM训练算法步骤如下：①前向计算神经元ft、it、ct、ot、ht的输出值；②通过沿时间的反向传播计算各个时刻误差项，再将误差项向上一层传播；③按照相应的误差项，计算每个权重的梯度。

2 动态预测模型建立

2.1 研究区滑坡概况

新滩滑坡位于湖北省秭归县西陵峡段，属于堆积层滑坡。滑坡长度约2 km，面积0.73 km2。岩层与上游河段倾角25～38°[14]，西侧是堆积层物质的主要来源，紧邻一二叠系砂岩和灰岩组成的陡崖，深300～450 m[15]；东侧为低山丘，主要物质由志留系页岩组成，来自志留系。滑坡向南延伸至江边高程约65 m，平均坡度23°。滑前坡体中部有两级横向陡坎，一为走向NE30″，坡度50～60°的姜家坡前缘陡坎，将斜坡分为上段(姜家坡斜坡)和下段(新滩斜坡)；另一陡坎在毛家院前缘，走向NE75″，将新滩斜坡分为毛家院台面和陡坎下2段。图3为滑坡变形监测点具体布设情况。

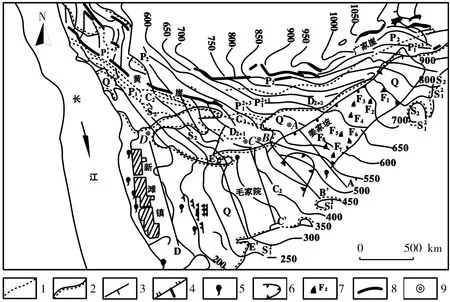
注：A、B、C、D—SHZ1-01、SHZ1-02、SHZ1-03、SHZ1-04；S2—志留系砂页岩；页岩；Q—第四系冲积层、崩积层、坡积层；P2—二叠系上统灰岩；C2—黄龙灰岩；D2+3—泥盆系石英砂岩；马鞍山煤组岩层；栖履组与第四组灰岩；A-A’—观测及其编号；1—地层界限；2—第四系与基岩界限；3—岩层产状；4——断层；5—泉水出漏点；6—滑坡变形边界；7—预留观测及其编号；8—陡崖；9—GPS监测点。

2.2 监测数据处理

根据新滩滑坡监测资料和调查记录，1977、1981年北侧的广家崖频繁发生较大规模崩塌。同年，专家和相关技术人员根据实地坡体情况布设监测点见图3。为进一步验证模型的可靠性，选取2011年4月到2012年6月4个监测点的位移数据作为本次训练样本。在进行训练之前需要对采集来的数据做“3δ”法数据异常剔除处理[16]。假设对某监测点进行了n次监测，所得的第i次监测值为Mι(i=1,2,…,n)，累积连续3次监测值为Ti-1,Ti,Ti+1(i=2,3,…,n-1)，则第i次监测的跳动特征定义为[17]：

hi=|2×Mi-(Ti-1+Ti+1)|

(9)

跳动特征值均值为：

(10)

跳动特征值均方差为：

(11)

相对差值为：

(12)

若Qi>3，则将该数据作为异常值剔除。

图4为处理后各监测点数据对比结果，纵坐标为水平位移，横坐标为第N次采集数据，以前15次采集数据为例进行数据剔除处理，可以看出处理前数据波动明显，处理后曲线较为平缓。

图4 “3δ”方法处理监测点数据前后对比

在利用“3δ”处理传感器采集来的数据后，还需对数据做归一化处理[18]，主要目的：①加快收敛速度；②避免大数据淹没小数据，提升预测精度。采用任意区间法，其步骤如下。

步骤一找到样本数据Y的最小值Min及最大值Max。

步骤二计算系数见式(13)：

(13)

步骤三得到[a,b]区间的归一化数据，见式(14)：

norY=a+k×(Y-Min)

(14)

在函数运算过程中，输入的取值直接影响着模型的性能，输入选值不当会导致输出数值落在曲线饱和区，为防止Sigmoid开函数两头饱和区对实验造成误差影响，本文选用函数中段的函数关系进行运算[19]。

2.3 LSTM动态建模算法流程

图5为LSTM动态建模算法流程。首先进行初始化，包括学习速率、期望精度Ti、各层初始权重Wij等；然后输入给定向量值，求出目标输出值并与给定值进行偏差值Ej计算，判断其是否满足误差精度要求，否则对所有各层之间权重进行更新，直到偏差满足预期给定期望值时，迭代停止，训练结束。

图5 LSTM动态建模流程

本文采用“流转训练”方式对数据进行训练，如根据前3组4个监测点的采集数据，预测第4组4个监测点的数据，依此类推，表1为网络训练过程[20]。

3 工程应用及算法验证

3.1 训练和测试数据选取

滑坡体形变是一个复杂的非线性演化过程，合理选择参数配置可以有效提升模型的预测精度，选择输入层个数并不是越多越合理，输入数量太多有可能会导致训练效率低，影响网络训练精度等问题。隐含层的节点数的选值需要根据转换函数的型式、样本数据特性以及要解决问题的复杂程度进行匹配。此外，为避免网络模型没有泛化能力，即网络模型的系统误差与训练样本的特性无关而趋于0。隐含层节点个数还需满足小于N-1(其中N为训练样本数)，因此合理的设置参数配置显得尤为重要。本文采用网格搜索法进行参数寻优[21]，最终设定输入节点数为12，隐藏层节点为18。本文总共选取200个[22]数据，其中每个监测点采集50次。

3.2 新滩滑坡位移预测

以新滩滑坡2011年4月到2012年6月，4个监测点SHZ1-01、SHZ1-02、SHZ1-03、SHZ1-04所采集的数据作为本次实验的样本来源。本文选取SHZ1-03监测点对其进行分析，其中70%作为输入数据用于预测模型的建立，30%用于检验。本次训练以第42期监测点的数据为预测目标，前41次采用“流转训练”的方式，训练中所有数据为量化处理后的值。图6为RNN和LSTM训练实测-预测，图7为RNN和LSTM训练误差-迭代，表2为训练后输出的预测结果和训练所用时间值。图6所示，横坐标为组数，纵坐标为位移量化值(归一化值)。比较图6，可知LSTM预测曲线与实测曲线的拟合度更高。究其原因，RNN存在梯度消失现象，无法处理长序列数据：即当进行某一轮训练时，某一时刻梯度已减小为0，并且从此刻以后所得到的梯度都近似为0，其对权重数组W最终的梯度贡献为0(即W不再更新)。而LSTM由于算法结构的特殊及复杂，可以解决梯度消失问题并且提高预测精度。

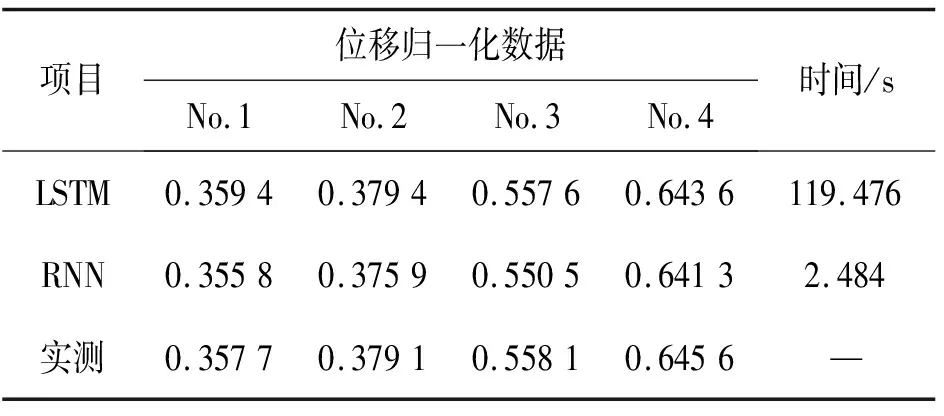
表2 各算法针对第42次数据进行验证的结果比较

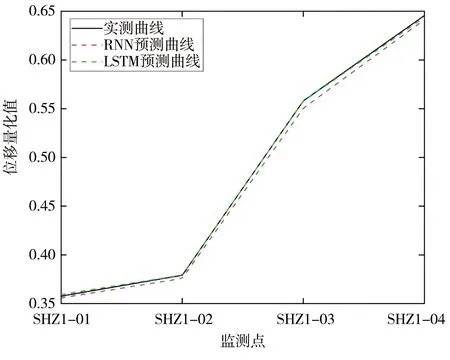
图6 实测-预测结果

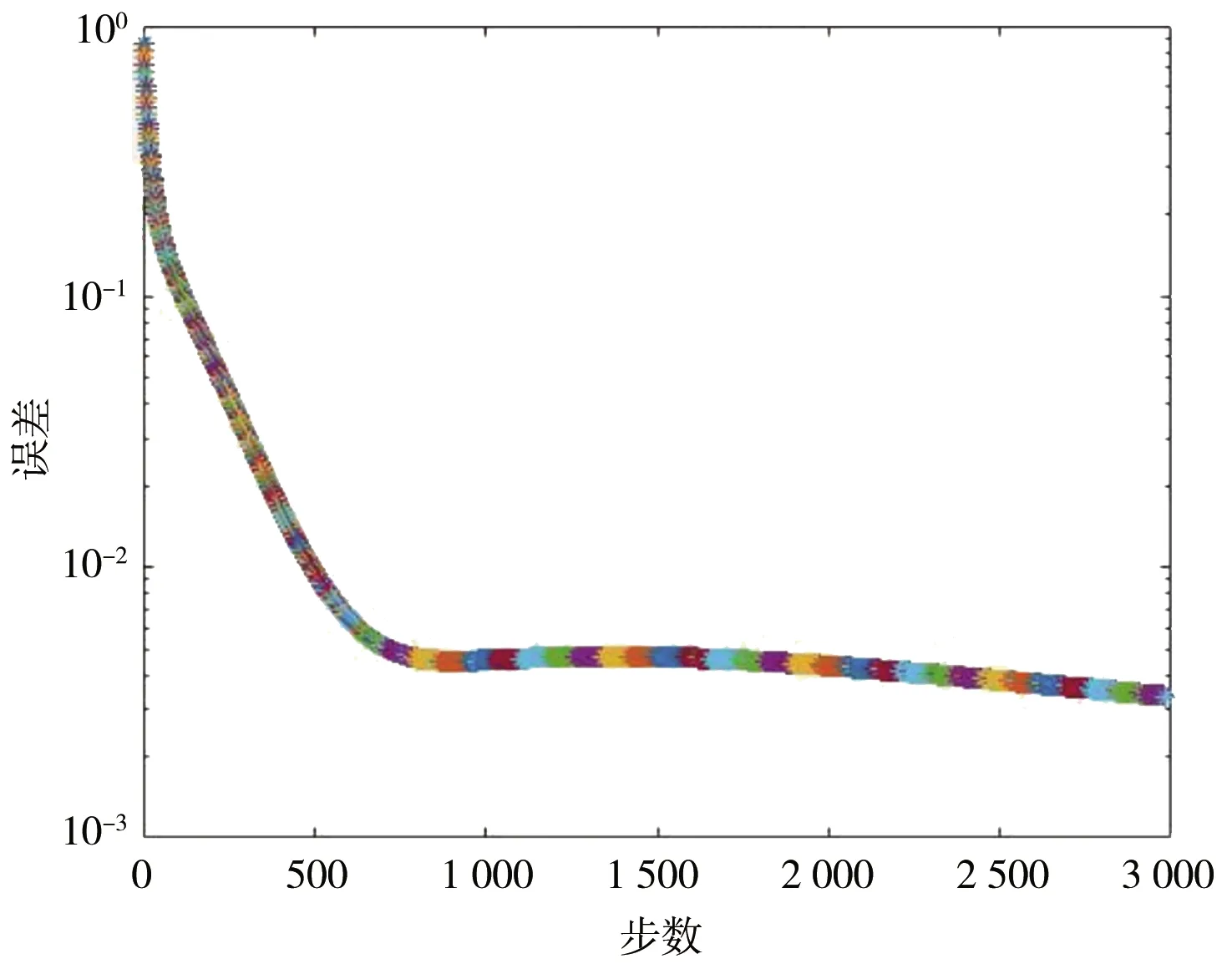
本次训练中预设期望精度为0.003，2种算法初始学习速率均为0.001，每经过1 000步长，学习率衰减0.1倍。图7所示，当迭代步数为500时，RNN训练结果的误差约为0.009 7，未达到目标要求。而LSTM训练结果的误差约为0.001 9，此时已满足预设期望精度；当RNN训练满足预设期望精度时，此时迭代步数为3 000，而LSTM在迭代步数为3 000时的误差约为0.000 03，显然LSTM训练算法结果更优。

a)RNN

LSTM由于引进了“门”以及其算法内部结构、参数的复杂，使其在处理长时序数据的能力大大提高，但其在预测计算时间上比RNN要慢。表2中RNN训练所用时间为2.484 s，LSTM训练所用时间为119.476 s，得出RNN的训练时间比LSTM约快50倍，验证了上述观点。图6曲线可得LSTM算法预测较RNN预测拟合程度更高。图7(RNN误差-迭代)实际训练误差接近0.003与(LSTM误差-迭代)实际训练误差接近0.000 03相比，LSTM训练的误差精度比RNN训练的误差精度更高。基于以上数据结果，更加印证了RNN循环神经网络在处理距离较近的信息方面的优势，也表明了其在处理距离较远信息时能力不足。而在本次滑坡位移预测实例中，2种算法的计算时间可忽略，因其位移的演化是一个逐渐累积的过程，需要的时间远大于计算机预测所需的时间。

通过对比2种算法位移预测值，实验结果表明2种算法整体的预测结果基本一致。为验证模型的科学性，本文选用平均绝对误差(MAE)、平均相对误差(MAPE)2个评价指标进一步评估模型预测精度[23]，见式(15)、(16)：

(15)

(16)

式中c——实际测量值；ci——预测值；n——组数。

以No.3监测点为例，表3为该监测点应用2种算法后的MAE与MAPE指标评价结果对比。

综合表3可得，LSTM算法训练的效果总体优于RNN。2种算法中，LSTM训练后的结果更靠近实际值；在数值上，MAE与MAPE 2项评价指标，LSTM明显小于RNN。

图8所示，比较2种算法的预测曲线与实测曲线，LSTM的预测曲线基本与实测曲线吻合，可见LSTM训练模型的效果更好。以表3中第5组为例分析(图9)：RNN的预测值与LSTM的预测值在一定范围内都满足要求，而在计算误差之后，RNN模型训练的MAE为0.024 1，LSTM模型训练的MAE为0.006 0，显然LSTM模型训练后的MAE更小，表明LSTM收敛程度要高于RNN。表4为第5组、第6组数据分别在2种算法下的MAE与MAPE偏差。

表3 No.3监测点2种训练MAE、MAPE值

图8 RNN、LSTM实测

a)MAE

表4 2种算法MAE与MAPE偏差

表4中LSTM的MAE与MAPE偏差明显大于RNN，表明第6组预测值存在异常，输出不稳定。究其原因在RNN与LSTM训练过程中，每一个循环的输出都依赖于上一层的ht-1与ct-12个因素。在计算过程中可能会出现当前ht或ct的前向计算被阻止或处于闲置状态，直到上一层的ht-1、ct-1的整个计算完成，才会进入下一循环。

4 结语

针对新滩滑坡实时变形进行的动态预测，本文选用2种适用于建立动态模型的算法RNN与LSTM，并应用于新滩滑坡实际工程中，结果表明LSTM比RNN在滑坡位移预测中的总体效果更优。

a)LSTM算法预报精度更高。由图7可知，当RNN训练步数达到3 000步，误差函数满足期望精度时，LSTM和RNN的训练误差分别为0.000 03和0.003，表明LSTM比RNN的训练结果更精确。表2中LSTM和RNN在本次训练中计算所用时间分别为119.476、2.484 s表明：LSTM算法结构比RNN更为复杂，其动态模型的参数与训练样本数目也相对较多，训练结果更加具有可靠性。

b)滑坡预测的结果可转化为滑坡风险预测，因此LSTM动态模型算法可应用于预警预测中，防止灾害的发生，保障人民的生命和财产安全。