模糊层次分析法与改进遗传算法的选址仿真*

田子平，田淑芳

（中国地质大学地球科学与资源学院，北京 100083）

0 引言

在信息化的作战背景下，随着高新技术在军事作战领域的广泛应用，战场环境瞬息万变，战场中信息处理与资源调配的效率时刻影响着战局。作战双方在指挥领域的博弈异常激烈，指挥设施成为作战双方的重要打击目标，军事指挥中心的安全性与作战效能显得尤为重要。因此，提高指挥设施的抗打击能力，最大限度地发挥其指挥作用要从两方面入手，一方面是发展先进的武器装备，增加武器装备对不同作战环境的战斗性能，进而提高战争硬实力；另一方面因指挥中心位置的选择很大程度上决定了我军指挥能力的发挥与战场信息的掌握，关系到指挥领域博弈的胜败，通过模拟仿真的方法，增强其隐蔽性和机动性，提高作战软实力。如何科学高效地选择指挥中心的位置，目前，国内外学者及军事科研部门进行了大量的军事设施选址研究，国内学者龚延成［1］提出了一种基于层次分析法的战时后勤设施选址方法，选取了隐蔽条件、交通条件、展开条件和水电条件构建层次结构模型，并进行了选址过程的演示分析。国外学者Bahar Sennaroglu［2］等将层次分析法与优劣排序决策法、多准则妥协解排序法相结合，设置军用机场为选址目标，研究内容更加侧重理论研究与方法比较，未涉及实际案例的模拟计算。传统军事选址方法选取地形、植被等自然因素，借助专家经验及资料图件，普遍采用层次分析法进行适宜性评价，存在评价因子选取不全面、未考虑模糊特征和缺少实际问题中重复选址的可行性验证等问题，利用传统方法解决实际问题时存在较大的误差，可能影响选址结果，耗费更多的战备资源。

针对以上问题，本文对传统的选址方法进行了创新与改进：整合基于Landsat 8 OLI 和国产高分数据的军事遥感解译成果，借助GIS 平台从中提取评价因子，利用模糊层次分析法（Fuzzy Analytic Hierarchy Process，FAHP）［3-4］定量地实现了各个评价因子的可视化，建立军事指挥中心选址评价体系，计算得出各评价因子的权重，进而构建选址模型，揭示其在空间维度上的适宜性。以适宜性评价结果为基础，采用遗传算法（Genetic Algorithm，GA）［5］编程求解具体位置的坐标，引入马尔科夫理论（Markov）［6］改进遗传算法，实现决策过程的迭代运算，验证选址流程的可行性与有效性。本文提出的模型方法旨在提高解决选址问题的效率与准确性，为军事设施选址决策提供一定的理论基础与科学依据。

1 军事指挥中心选址评价指标体系

针对本文研究目标，由于武器型号参数、攻防能力不便于获得，本文建立军事指挥中心评价体系是建立在我军野外陆地作战武器装备（指挥装备、通信装备、作战装备等）能够在小规模野战中发挥效能的基础上。阅读军事设施选址相关文献，学者翁东风等［7］分析了高技术条件下军事设施选址的特点，从空间距离、自然环境和建设成本3 个方面研究建立了选址多目标决策模型。本文考虑到军事指挥中心选址问题的特殊性，除工程建设条件之外，还应引入军事和后勤相关因素，使得评价体系更加完善。评价体系总体结构为目标层，一级指标层包括工程地质，地形地貌，军事作战和后勤保障4个一级评价因子，二级指标层包括岩性、地形、植被、公路等12 个二级评价因子，如表1 所示。

表1 军事指挥中心选址评价指标体系

军事设施的建设首先需要考虑岩性和断裂因素，硬度较大的岩石保障设施安全，本文按照岩石的坚硬程度进行岩性划分；断裂对工程设施的危害体现在断裂带处易发生崩塌；工程建设也要远离滑坡、崩塌和泥石流等地质灾害。地表形态直接影响建筑总体位置的选择，因此，选址问题也要考虑到地形起伏度、坡度和地貌因素。在实际作战中，考虑到指挥中心的重要性及特殊性，应选择植被茂盛易于隐蔽的区域。两军交战，我方指挥中心容易遭到打击，为了保证人民群众的安全，应远离居民区、城镇等人员密集的区域，同时其位置的选择应远离党政机关驻地，以保护政府人员及设施，维护政府基本职能。后勤保障是军事指挥中心正常运行和效能发挥的基本条件，同时又关系到人员与资源的调配，因此，引入发电站、水系和公路评价因子构建评价体系［8］。

2 军事指挥中心选址模型构建

2.1 评价因子权重计算

军事指挥中心选址结果取决于一级和二级指标层评价因子的适宜性等级分类，所以，选址问题可以转化为多个评价因子按照权重的叠加，得到空间适宜性分类结果。本文利用模糊层次分析法进行各评价因子权重的计算。

传统的层次分析法具有定量、客观的优点，可以将复杂问题层次化，但是当某一层次评价指标很多时，其思维的一致性很难保证。模糊层次分析法改进了传统的层次分析法，引入模糊数和模糊集的概念，分析决策问题的不确定性，判断结果用模糊数代替精确数，有效地解决了决策过程中不确定条件的量化问题［8］。利用模糊判断矩阵A 确定评价因子权重：

式中，n 为每个指标层中评价因子的个数，矩阵中aij=（lij，mij，uij）为三角模糊数，代表指标Ci相对于指标Cj的重要程度，lij和uij分别为下界和上界，mij为lij和uij的中值，矩阵中aji=（1/uijj，1/mij，1/li）为对应的逆三角模糊数［9］，三角模糊数所表示的重要性级别参照文献中前人的研究［10］，如表2 所示。本文将采用专家打分法，将每个指标层中的各个评价因子进行重要性的两两比较，填入重要性语义等级对应的三角模糊数，进而生成每个指标层的模糊判断矩阵A。

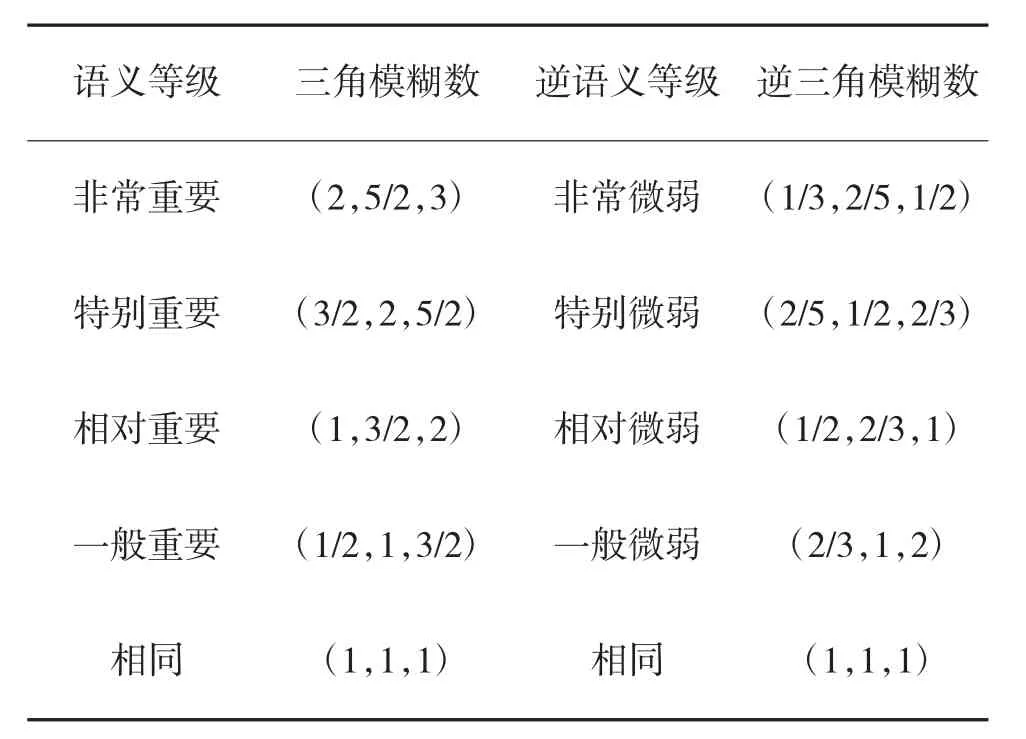
表2 表示重要性语义等级的三角模糊数

构建模糊判断矩阵A 后，进行矩阵的一致性检验，一致性指标CI（Consistency Index），考虑到一致性的偏离可能是由于随机原因造成的，因此，引入一致性比率CR（Consistency Rate），计算公式如下。CR＜0.1 时，认为该判断矩阵通过一致性检验，否则，应调整aij，直到CR＜0.1 为止。

2.2 评价因子适宜性分类

本文以专家专业分析与军事遥感数据为基础，判断各评价因子的适宜性，将每个二级指标分为4类，以数字进行赋值，即最适宜区域为4，适宜区域为3，不适宜区域为2，最不适宜区域为1。具体评价因子的适宜性分类范围如表3 所示。

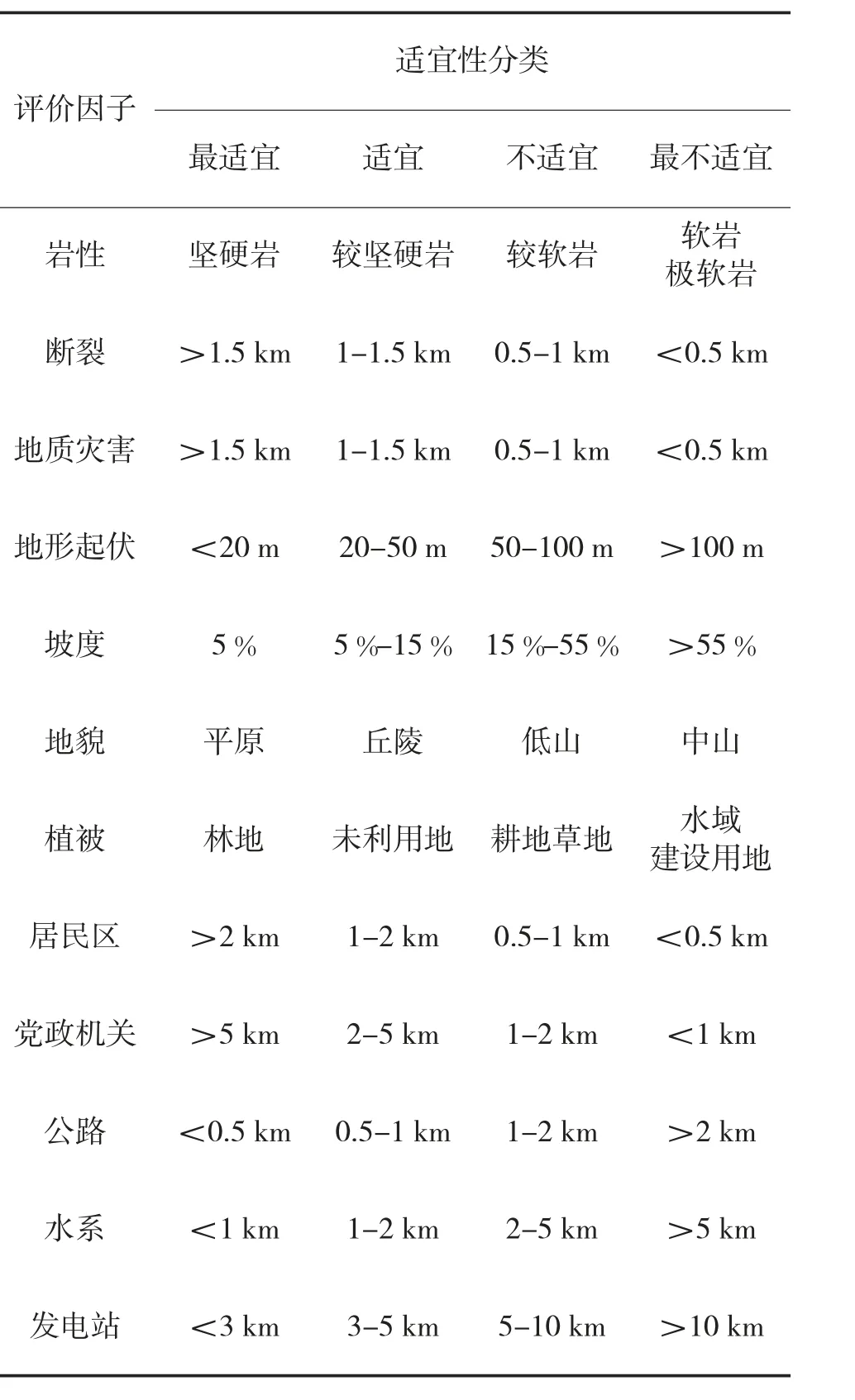
表3 评价因子适宜性分类

3 实例分析及可行性验证

为了验证军事指挥中心选址模型的可行性，本文选取东北边境中北部为研究区进行实例分析，研究区位于中国的东北部，以中朝边境为中心线向国内延伸30 km～80 km，覆盖地理坐标范围为125°07'44"E～130°49'53"E，40°49'39"～43°11'36"N。研究区总面积为25 000 km2，流经水域为鸭绿江和图们江，涉及我国的吉林省3 个地市14 个县，主要包括通化市、集安市、白山市、长白朝鲜族自治县、延吉市等大型城市。

3.1 数据预处理

本文以《东北边境1∶25 万遥感地质解译与查证》项目为依托，在充分收集东北边境地区（中、北部）已有地质环境、地质矿产、生态环境等相关资料基础上，以国产卫星数据（GF-1、GF-2、ZY-3 等）遥感影像数据为主要数据源，Landsat-8 卫星数据作为辅助，采用遥感图像处理、专题信息增强、人机交互式解译与野外实地验证方式相结合的信息提取方法，以现代遥感技术为主要手段，在该地区开展基础地质、工程地质、水文地质、地形地貌、土地覆被、矿产资源、地质灾害、交通信息和重要目标9 个专题的遥感调查工作。获取东北边境地区（中、北部）1∶25 万解译成果数据，专题调查结果经过野外实地验证，专题解译成果准确率均在90%以上。考虑到研究区与选址目标的面积和解译成果数据的精度，针对评价尺度的一致性和异质性，所有数据在转换为统一坐标系统后再转换为50 m×50 m 的分辨率格网，数据的准备和分析工作统一输入GIS 平台进行综合处理。

3.2 评价因子权重计算

为保证适宜性评价的客观性，本实验邀请项目组军事领域专家对指标之间相对重要性进行打分，运用模糊聚类算法剔除偏离较多的三角模糊数，经过对不同专家的多轮匿名征询和数据反馈，专家组成员的意见逐步趋于集中，确保所有矩阵的一致性指标均在0.1 以下，最终采用模糊层次分析法计算出各评价因子权重，如表4 所示。在一级指标层中，工程地质与地形地貌为工事建设的基础，因此，二者相对于军事作战与后勤保障更为重要。在二级指标层中，岩性适宜可以保证建筑的稳定性，地形起伏度决定了建设的难易程度，应尽可能地建设隐蔽以防止敌军轰炸，距离公路较近易于实现人员物资的调配，在后勤保障中起决定性作用。结合野外调查，计算得出的评价因子权重符合东北边境中北部实地情况。

表4 评价因子权重

3.3 选址适宜性评价及位置求解

将经过重分类的评价因子图层和模糊层次分析法计算得到的评价因子权重输入GIS 平台，进行网格图层的综合叠加分析，最终得到东北边境中北部军事指挥中心适宜性评价图，如下页图2所示。从图中可以看出，研究区范围内绝大部分都是军事指挥中心选址适宜区域，分布范围较广，最适宜区域主要分布在中部，距离边境河鸭绿江较近；不适宜区域集中在西北方位，房屋住宅较密集、植被较少；最不适宜区域较分散，主要为河流及其附近地区。

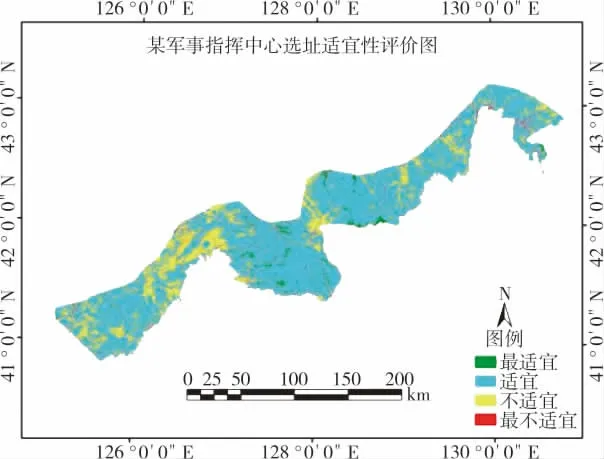
图1 军事指挥中心选址适宜性评价图

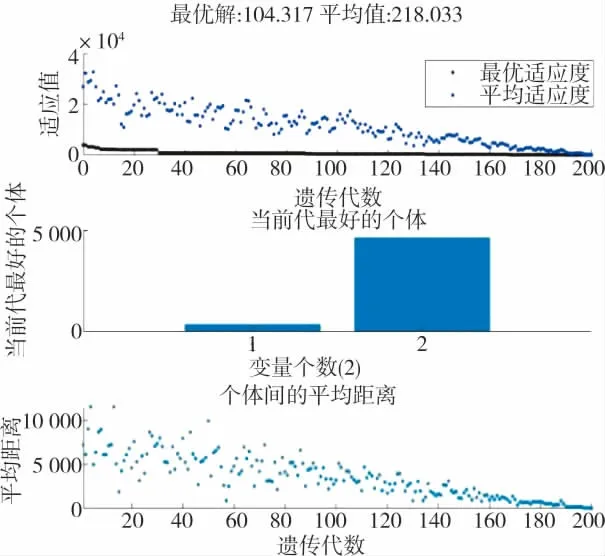
图2 遗传算法计算结果

本文采用遗传算法进行具体位置坐标的求解，遗传算法的优势在于全局搜索能力较强，具有较好的收敛性。首先进行情景设定，假设根据应用模型所确定的一处指挥中心被敌方战斗机等新型战争武器从空中炸毁，我军急需将人员、武器等物资转运到另一个指挥中心，同时也需与附近其他指挥中心取得联系，实现人员物资的快速调度。为满足时效性的配置要求，实现军事效益最大化，应确定另一处指挥中心与其他指挥中心之间的最短路径。假定已知5 个军事指挥中心的位置，对应的地理坐标分别为A1（370.26，4 626.46）、A2（391.32，4 633.26）、A3（366.46，4 641.64）、A4（376.72，4 649.89）、A5（394.00，4 646.50）。其中，A1 位置已被敌军炸毁，考虑到指挥中心之间的人员调配与物资转移，现确定A6 位置，A6 需满足到达A1、A2、A3、A4、A5 的总路径最短，因此，将选址问题简化为求解目标函数最小值问题，目标函数即适应度函数为：

遗传算法运算中所涉及的参数设定包括初始种群［0，5 000］，种群尺度大小设置为20，选择参数为随机均匀分布，再生参数代表产生下一代个体的方式即进化方式，其中，生存到下一代的个体数设置为2，由交叉产生的个体所占比率设置为0.8。

实验结果表明，运行到第200 代时，结果开始趋于稳定，因此，设置终止进化代数为200，取第200 代为最终结果，如图3 所示。最终得到最适宜的指挥中心的地理坐标为（379.486，4 630.487），该点距离5 个指挥中心的最小距离之和为104.32 km，且位于选址模型确定的适宜区内，如图4 所示。

图3 军事指挥中心位置

3.4 选址方法可行性验证

军事事件具有突发性，选址的可行性需经过多次验证，而选址问题属于土地利用类型转换问题，经过国内外学者多次研究验证，土地利用类型的变化过程遵循马尔科夫理论，利用马尔可夫模型可以进行土地利用类型变化的预测［11］。因此，本文引入马尔科夫理论验证选址方法的可行性，马尔科夫理论，简单来讲系统未来的状态与系统过去的状态无关，仅取决于系统现在的状态。实例中已知A1 位置已被炸毁，军事指挥中心转移到A6 位置以后，系统现在的状态为A2、A3、A4、A5、A6，下一次军事事件造成的结果仅取决于现在的状态，假设此状态下的任意位置再次被炸毁，需要重复进行选址过程。基于以上，本文改进了遗传算法，实现了遗传算法的自我迭代。

实验结果表明，经过改进遗传算法的8 次迭代，计算得到的军事指挥中心地理位置仍位于选址适宜区域内，改进遗传算法的结果即验证选址方法可行性的同时模拟出更多的选址位置。与传统的遗传算法相比，新的算法解决了以往军事设施选址研究中无法进行重复计算具体位置的问题，同时也验证了本文提供的选址方法具有一定的可行性，使得现代战争中选址决策更加高效完备。

4 结论

本文创新地将模糊层次分析法、遗传算法与马尔科夫理论相结合，应用于军事指挥中心的选址问题，以模糊层次分析法设置指标层并计算评价因子的权重，以某部为研究区，将遥感解译数据输入GIS平台得到选址适宜性区域，基于适宜区进行遗传算法编程计算具体地理坐标，引入马尔科夫理论改进遗传算法实现了重复选址决策，总结以上，本文提出了一套科学有效的军事指挥中心选址流程方法。由于层次构建和权重分配都可根据具体地区的实际情况进行调整，本文提出的选址模型方法具有一定的普适性。然而，模型方法的改进不能弥补数据不足带来的负面效应，因此，应引入更多的评价因子，比如武器因素、战场因素、经济因素和效能因素等，可以使适宜性评价和选址位置的结果更加准确。同时，考虑到数据的精度与时效性，应进一步完善更新军事遥感解译数据，提高数据的准确性和实用性。对于模型方法而言，评价方法与求解算法仍需优化改进，以提供更完备的选址方法流程，为现代军事战争提供科学有效的指导建议。