基于改进NSGA-III 算法的动态武器协同火力分配方法*

于博文，吕 明

（南京理工大学，南京 210094）

0 引言

在防御作战场景下，武器- 目标动态分配（DWTA）问题是战斗指挥过程中较为重要的一个环节。一些学者将智能算法应用在处理武器-目标动态分配优化问题上，但是存在收敛较慢和优化效果差等问题，无法应对现代战场中复杂多变的作战态势［1-3］。如何有效提高防御场景下武器资源的整体作战效能，适应现阶段复杂多变的战场动态变化，将成为DWTA 问题的研究重点和难点。

武器-目标动态分配问题是典型的多目标约束组合优化问题，此类问题通常用多目标进化算法进行优化求解。多目标进化算法的发展趋势主要集中在求取Pareto 前沿，而非支配排序遗传算法（NSGA-III）［4］就是其中的典型代表，在处理多目标优化问题上具有较为广泛的应用，但是其收敛性存在一定不足。文献［5-7］引入自适应机制和Genetic K-means 聚类算法，通过其来保证解集的有效性和提高算法的收敛性。基于此，本文提出基于A-NSGA-GKM 算法的动态武器协同火力分配方法。建立以资源消耗最小、我方作战资源损耗最小，敌方剩余价值最小为优化目标的打击决策模型；建立基于A-NSGA-GKM 算法的动态武器协同火力分配优化模型；通过实验仿真验证基于A-NSGA-GKM 算法的动态武器协同火力分配方法的有效性。

1 动态武器火力分配决策模型

1.1 决策模型

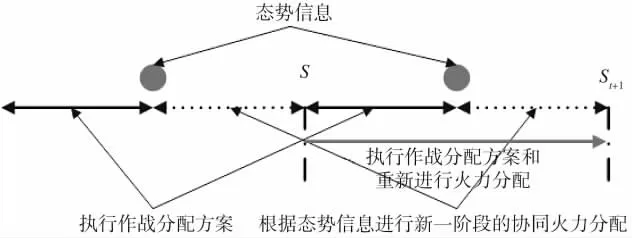
图1 动态武器协同火力分配过程

图2 s阶段决策变量x示例

1.2 优化目标

在实际拦截作战过程中作战资源有限，为了保证火力打击分配方案的有效性并完成拦截任务，因此，以敌方战场剩余价值最小、作战资源消耗最少、近距离作战武器损失价值最小为火力打击分配模型的优化目标，如式（6）所示，约束条件如式（7）～式（10）所示。

2 改进的NSGA-III 算法

根据上节描述的动态火力分配优化目标可以看出其属于多目标优化问题，因此，本文采用非支配排序算法（NSGA-III）［4］来对动态火力分配决策模型进行优化求解，如图3 所示。根据以往的研究，遗传算法在对解空间进行搜索时，交叉和变异的概率对算法的性能有着较大的影响［5］；NSGA-III 算法具有较好的多样性，但其收敛性较差［8］。

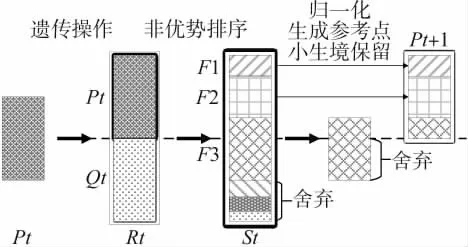
图3 NSGA-III 算法

2.1 自适应机制

在过往的研究中，大多是避免对一个较好的解集进行交叉操作，以免破坏解的结构。然而，该机制可能会使算法过早地收敛进入局部最优［9］。因此，本文提出一种新的自适应交叉机制，将较高的交叉概率应用在适应度函数较高的解上，假设其能够产生更好的解，这种自适应机制的目的是将上一代解中良好的解结构传递给下一代。

以本文优化目标举例，3 个优化目标均为最小化问题，即：min f 为其中一个优化目标，通过其来说明交叉概率Pc与变异概率Pm的自适应机制：

2.2 基于Genetic K-means 的参考点生成

Step1：染色体编码。将K 个分组聚类中心作为染色体上的基因编码（实数编码），如图4 所示。

图4 GKM 算法中的染色体结构示意图

Step6：重复上述操作步骤，直到达到终止条件（最大迭代次数）。

2.3 动态武器协同分配计算关键步骤

在遗传操作中加入自适应机制，保证优秀的解结构可以传递给下一代；在NSGA-III 的选择阶段引入GKM 算法，通过其对St解集中的优秀染色体实现自动分组聚类，在选取优秀染色体进入下一代种群时，以获得的聚类质心为选取参考点，选取PBI函数［10］较小的染色体计入Pt+1中，从而对NSGA-III的收敛性进行提升。通过本文提出的A-NSGA-GKM 算法，对动态武器协同打击火力分配进行优化求解，具体步骤如下：

Step1：种群初始化。染色体indi的编码如图5所示。

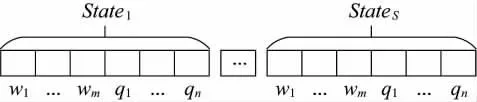
图5 编码示例

染色体indi采用整数编码，states表示第s 个作战拦截阶段，wm表示第m 个近距离作战单元要攻击的目标编号，qn表示第n 个远距离作战单元要攻击的目标编号。种群Pt的大小为L。初始迭代次数t=1，最大迭代次数为tmax。

式（15）～式（17）中，ind 为武器协同火力分配方案，M 为优化目标个数。

求解动态武器协同分配优化组合的流程如下页图6 所示。

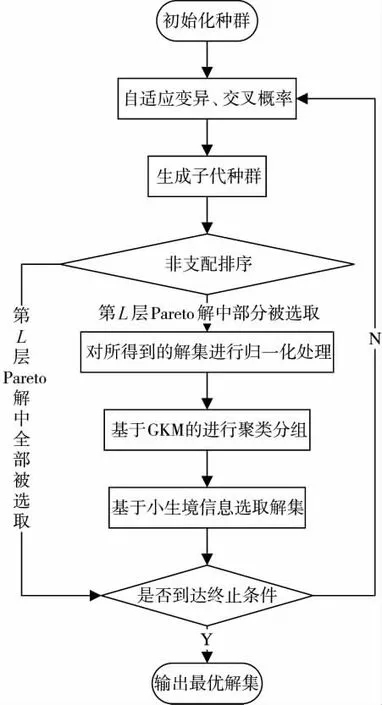
图6 A-NSGA-GKM 流程图

3 实验分析

3.1 实验算例描述

如图7 所示为本文算例示意图，假设我方拥有9 个近距离作战单元，4 个远距离作战单元，用来防御某重要资源，敌方有6 个作战单元进入我防区，本文将防御作战分为3 个阶段，敌、我双方作战效能都会随着作战持续下降，在每个作战阶段远、近距离作战单元最多有3 个单位同时攻击一个目标。通过获得的战场态势信息综合分析获得敌、我状态信息如图7 所示：

图7 本文防御作战算例示意图

目标反击系数为：

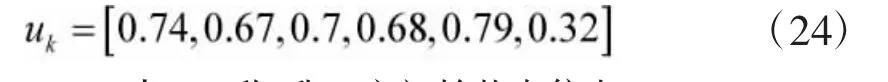
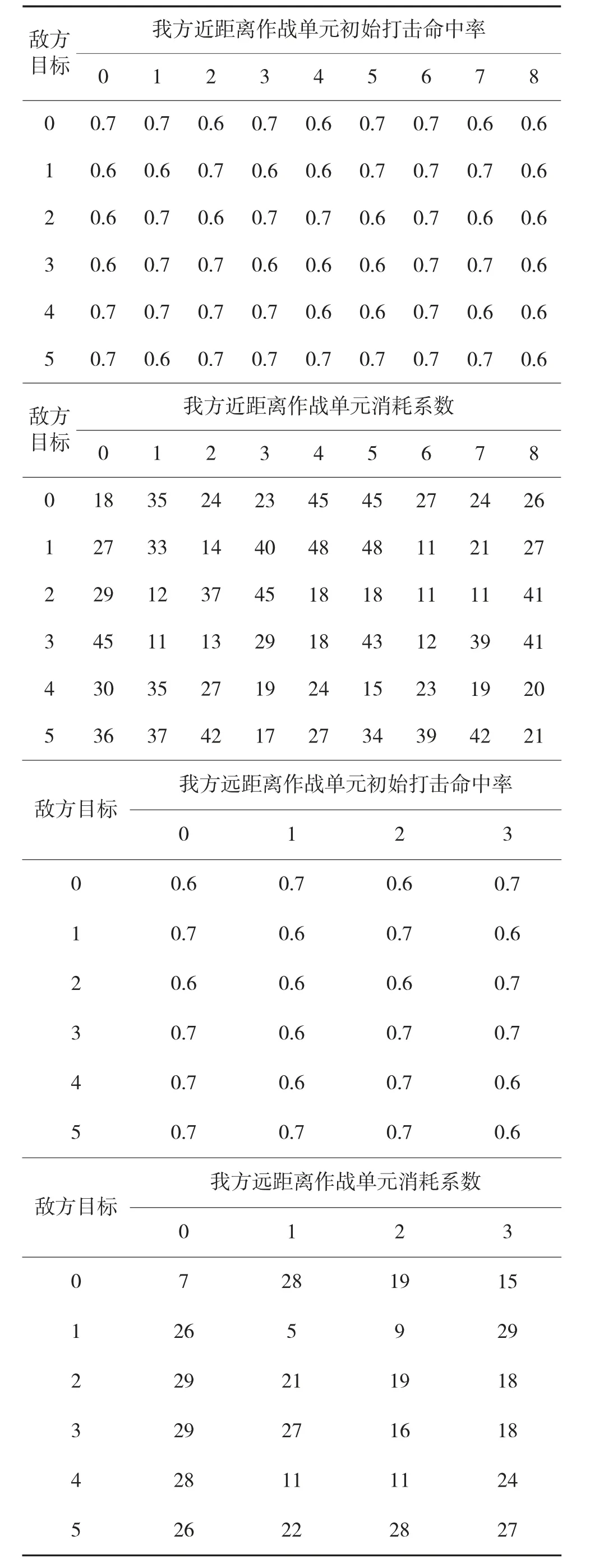
表1 敌、我双方初始状态信息

3.2 实验结果分析

A-NSGA-GKM 算法主要参数设置如表2 所示。

表2 A-NSGA-GKM 参数设置

独立进行3 组实验，每组实验进行40 次，结果如表3 所示，为A-NSGA-GKM（算法1）、NSGA-III（算法2）、NSGA-III-OSD（算法3）优化算法对协同火力分配模型求解的最优值。可得，第1、3 组实验中A-NSGA-GKM 算法与NSGA-III-OSD 算法相比结果相同或较优；所有3 组实验中A-NSGA-GKM算法的结果相对于算法均具有一定优势。

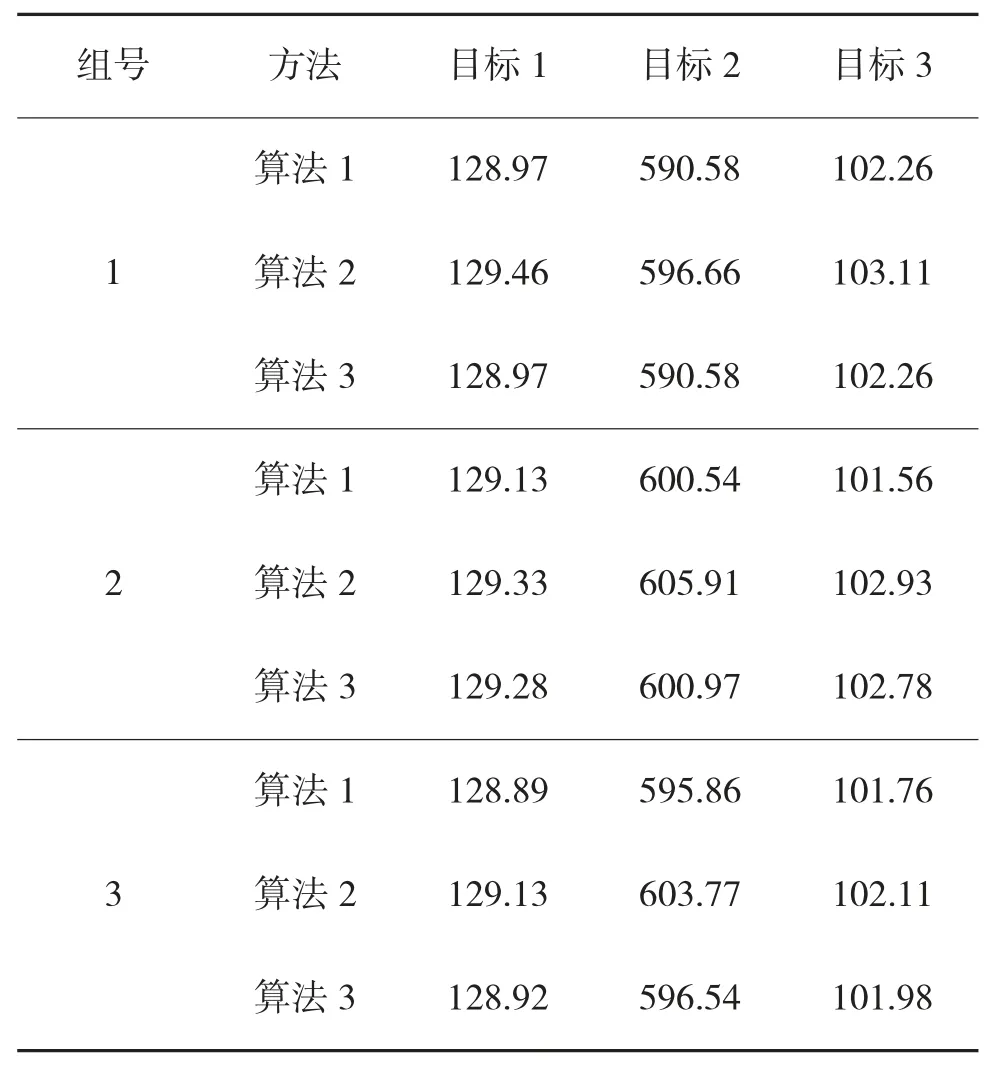
表3 各算法求得的最优解

通过HV（Hyper Volume）超体积指标和SC（Set Soverage）覆盖率指标对算法性能进行比较［8］。HV超体积指标用来衡量算法的收敛性和多样性，其数值越大，则解集的质量越高，通过大量实验，选取100 个参考点计算HV 指标其数值越大算法总体性能越好。通过SC 解集相互覆盖度指标来比较本文算法与对比算法产生的Pareto 解集之间的支配关系。统计上述3 组实验的HV 指标的统计值如表4所示，可以看出A-NSGA-GKM 在所有实验中均获得了最优的指标，证明其收敛性和分布性较好。

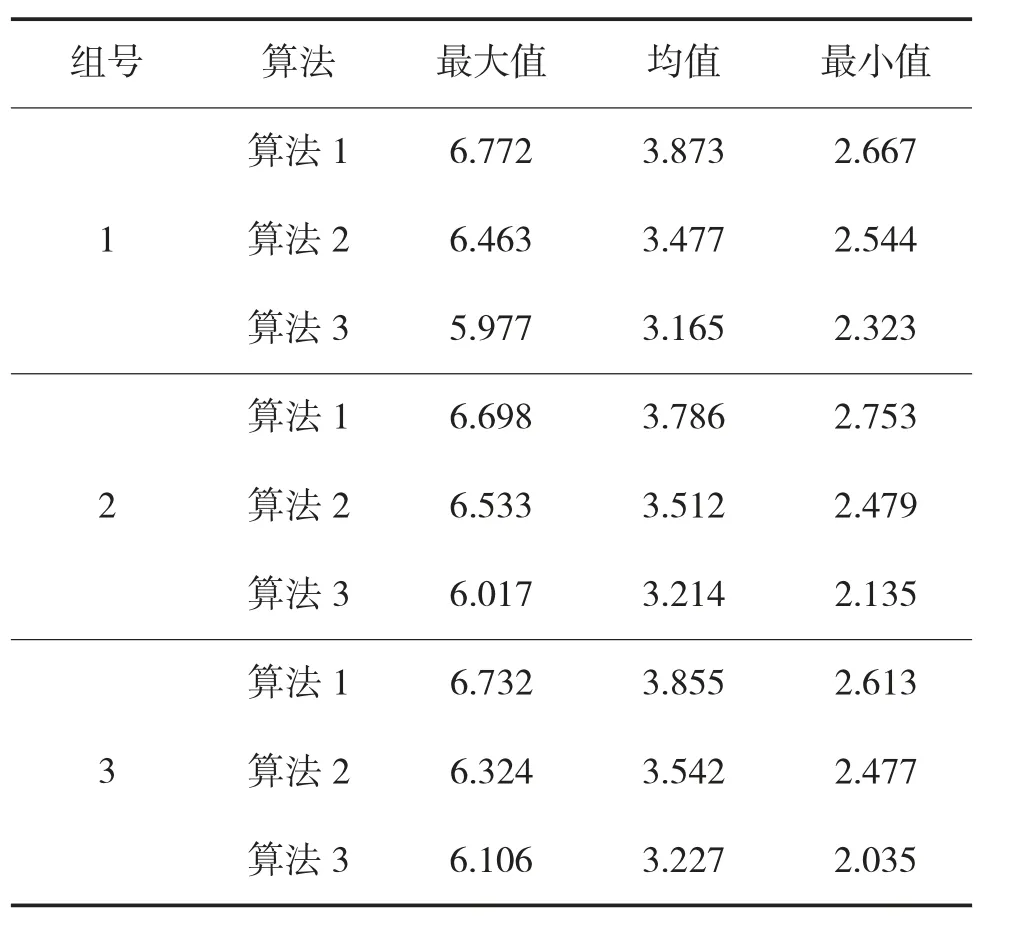
表4 各算法的HV 指标

整个实验过程中，SC 解集覆盖度指标如表5 所示，可以看出A-NSGA-GKM 的解总体上优于其他两种多目标优化算法。

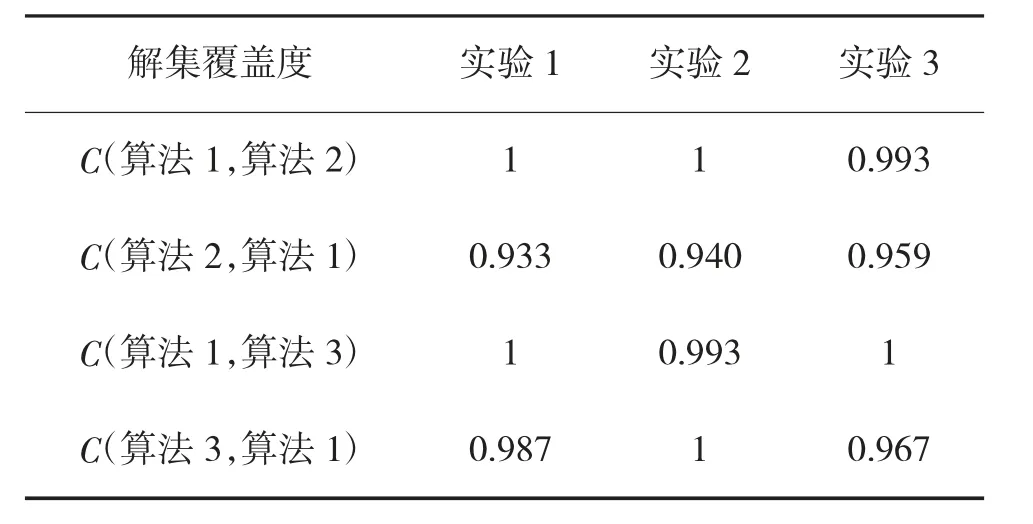
表5 各算法的解集覆盖度

实验平均耗时统计信息如表6 所示，可以看出上述3 种算法耗时最大值为87.416 5 s，最小值为85.184 5 s，满足通常情况下防御作战对目标分配的时间要求。

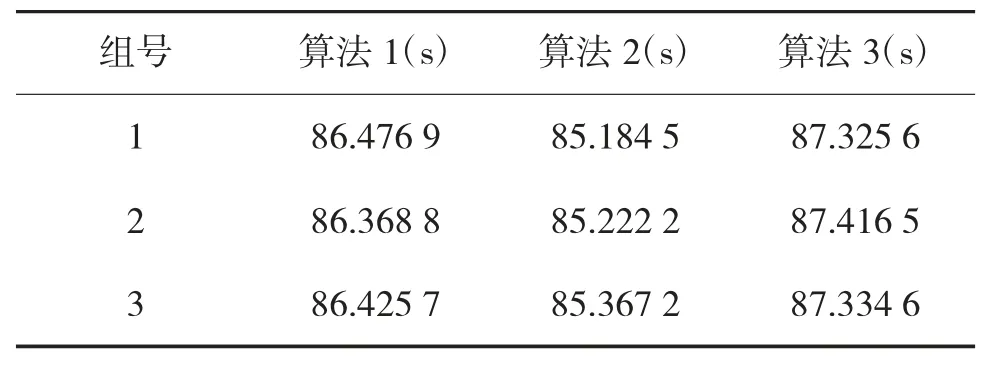
表6 各算法消耗时间（s）

从这实验结果中选取各算法优化结果HV 指标数值最高的解集分布，如下页图8 所示，可以看出A-NSGA-GKM 算法的解集分布，相对于NSGA-III和NSGA-III-OSD 的解集分布更加均匀。通过上述结论可以看出，A-NSGA-GKM 可以对武器协同火力分配进行有效的优化，具有可行性，解集分布更加均匀，收敛性更强，具有较为优秀的整体性能。

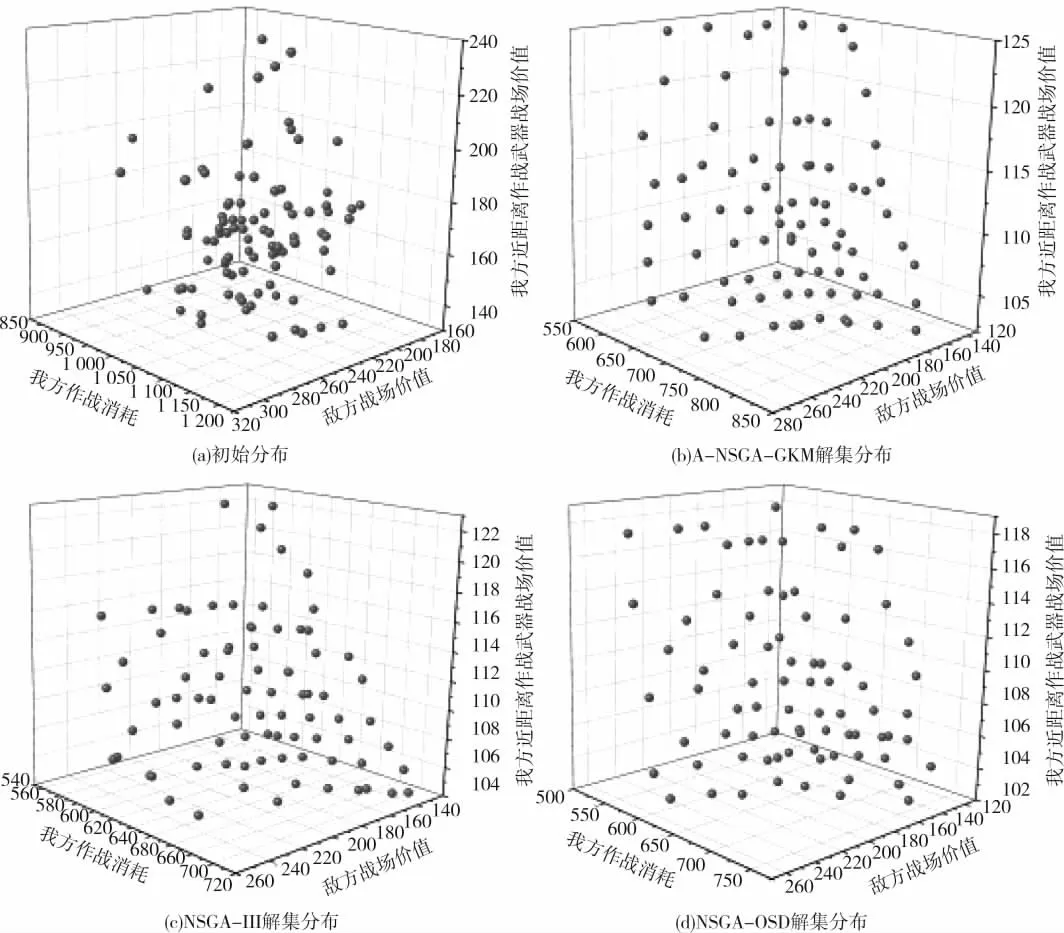
图8 在目标空间内得到的动态武器协同火力分配解集分布

本文提出的A-NSGA-GKM 算法在收敛性和优化效率上，相对于原NSGA-III 算法均得到提高，通过仿真实验证明了其可以有效处理动态武器协同火力分配问题。根据优化目标和实际作战态势从图8（b）中的Pareto 解来选取最终结果，如表7 所示。消耗要求较高，则以作战资源消耗为主要评价指标，如表7 情况2 所示，其具体分配方案如下所示：

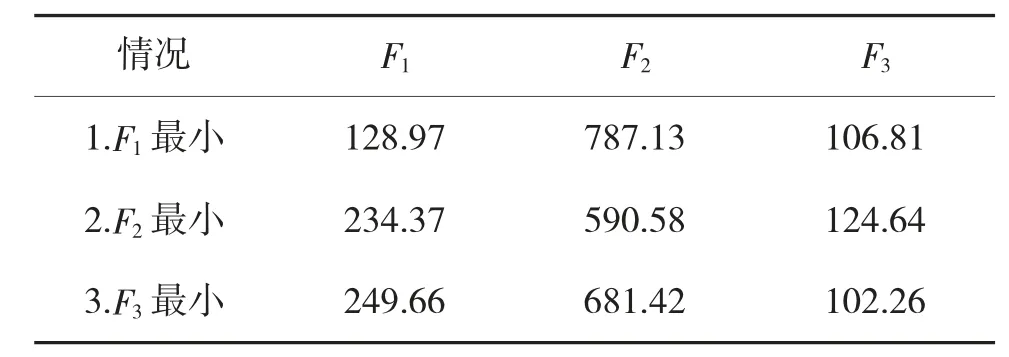
表7 动态武器协同火力分配优化组合

1）当作战资源充足时，消灭敌方作战资源作为主要评价标准，忽略其他两个指标，如表7 情况1所示，其具体分配方案如下所示：

3）当武器资源较为紧张时，则以作战武器损失价值为主要评价指标，如表7 情况3 所示，其具体分配方案如下所示：

2）当弹药等辅助资源较为紧张时，对作战资源

4 结论

针对动态武器协同火力分配问题，提出了一种基于算法的武器协同火力分配方法，引入自适应性保证优秀解集的结构，利用Genetic K-means 算法提高算法收敛性，提高了算法综合性能。该方法可以根据实际战场态势较好地完成武器协同火力分配，为动态武器协同火力分配问题提供新的思路，为战时作战指挥决策提供有效的辅助决策技术支持。