低模量基体对埋入式FBG传感器测量应变的影响
2021-09-07吴入军张晓峰郑百林朱灵杰
吴入军,张晓峰,陈 田,郑百林,朱灵杰
(1.上海电机学院机械学院,上海 201306;2.同济大学航空航天与力学学院,上海 200092; 3.卓郎江苏纺织机械有限公司上海分公司,上海 200240)
0 引言
与传统的电阻传感器相比,FBG传感器具有体积小、抗电磁干扰及质量轻等优点,因此在航空航天、土木工程等领域应用广泛。由于光纤与基体(被测结构)不是直接接触,造成光纤应变(测量应变)与基体真实应变不相等。因此,研究光纤应变与基体真实应变之间的应变传递理论具有重要意义。
国内外已有众多学者进行了相关研究。1991年,Nanni[1]等在混凝土结构中埋入FBG传感器,监测混凝土结构应变状态,通过实验方法发现光纤应变不等于基体应变。1992年,Pak[2]假定基体承受均匀应变,推导出基体和FBG传感器之间的应变传递关系,并得出保护层弹性模量和厚度对应变传递的影响。1995年,赵占朝等[3]对埋入FBG传感器的混凝土结构中产生内部应力集中问题进行了研究。1998年,Ansari[4]等首先利用剪滞原理,对FBG传感器应变传递机理进行重新分析,并且在等强度梁上对不同粘结长度的FBG传感器进行了实验验证。2002年,Li[5]等将保护层假定为理想弹塑性材料,对FBG传感器受拉受压情况分别进行了分析。李东升等[6-8]在Ansari研究基础上,修正了光纤、保护层和基体中间处的应变相等的假设,并且提出光纤和保护层轴向应变传递率近似相等的假设。吴永红等[9-11]对FBG传感器光-力转换方程以及光-力转换方程的非线性时变方程进行了研究。刘德华等[12]将FBG传感器埋入混凝土结构中,用来研究光纤应变与基体应变之间的关系,建立了应变传递方程;柴敬等[13]将封装后的FBG传感器埋入水泥砂浆中,用以监测岩层深部的变形情况以及其发展状况,并利用FBG传递理论进行了分析;梁德志等[14]利用有限元方法对埋入混凝土中的FBG传感器应变传递率进行计算和分析;吴入军等[15]提出多项式形式的剪应力表达式,基于此建立应变传递方程,经验证具有较高精度。
虽然国内外学者进行了较多研究,但都是假定基体应变为恒定,忽略FBG传感器对基体应变的影响,但是,当FBG传感器埋入低模量基体材料时,FBG传感器的存在会改变基体的应变状态,因此,在该情况下建立基体应变与光纤应变之间的关系时,必须考虑两者之间的耦合作用。
1 理论公式推导
埋入式FBG传感器结构包括光纤、保护层、粘结层和基体,假设基体轴向预应变为ε∞,详细结构和受力分布如图1所示。图1中,rf、rc、rm分别为光纤半径、保护层外径以及粘结层外径;σ为轴向应力;τ(x,r)为剪切应力;粘结长度为2L,L为半粘结长度;下标f、c、a和m分别表示裸光纤、保护层、粘结层和基体。

(a)FBG传感器轴向/横向截面示意图
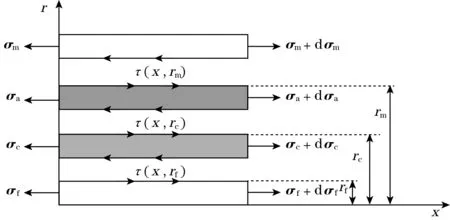
(b)各层应力图图1 FBG传感器示意图
本文理论公式推导基于以下假设[8]:假定FBG传感器各层之间的界面为理想界面,无相对滑移;所有的材料均为线弹性材料。
对裸光纤建立平衡微分方程:
(1)
式中τ(x,rf)为光纤与保护层之间界面上的剪应力。
由式(1)得到:
(2)
建立保护层和粘结层微分方程如下:
(3)
(4)
式中:τ(x,rc)为保护层与粘结层之间的界面剪切应力;τc(x,r)和τa(x,r)分别为保护层和粘结层的剪应力。
由式(2)~式(4)得到保护层和粘结层剪应力表达式:
(5)
为进一步提高计算精度,李东升[6-8]提出以下假设:
(6)
将式(6)代入式(5)中得到:
(7)
轴向变形是主要的,可以忽略径向变形[8],则存在:
(8)
式中:u和v分别为轴向和径向位移。
将式(7)带入式(8)并积分,得到:
(9)
式(9)的积分结果为
(10)
式中:um(x,rm)、uf(x)为基体和光纤的轴向位移。
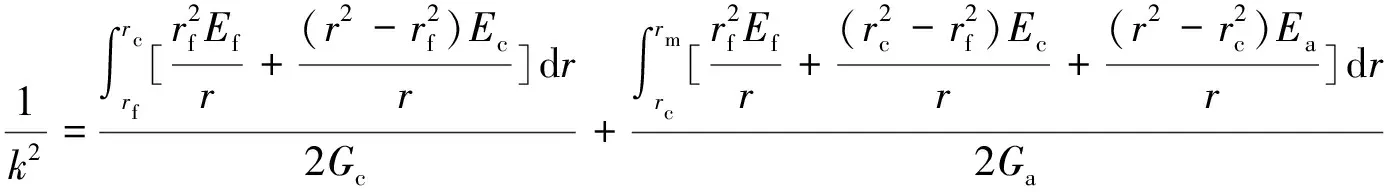
(11)
对式(10)求导数得到:
(12)
式中:εf(x)、εm(x,rm)为光纤应变和基体应变。
对式(12)进行简化为[16]
(13)
式中εm(0,rm)为FBG传感器与基体粘结区域中心处的轴向应变值。
对式(13)求解得到:
εf(x)=c1ekx+c2e-kx+εm(0,rm)
(14)
参数c1和c2由以下边界条件决定[3-13]:
εf(L)=εf(-L)=0
求得c1和c2的解为
将参数c1和c2带入光纤应变方程(14)中,得到FBG传感器光纤应变方程为
(15)
因此,得到FBG传感器应变传递率为
(16)
FBG传感器的测量应变为光栅长度方向上的平均应变,因此平均应变传递率可以表示为
(17)
式中:ε∞为作用于基体上的轴向均匀预应变;εm(0,rm)为基体粘结中心区域的轴向应变值。
基体内侧粘结区域的剪应力为
(18)
式中Eeq为FBG等效刚度。
对式(18)进行傅里叶变换得到:
(19)
在以下部分将基体看做空间轴对称结构,利用傅里叶级数和贝塞尔函数方法,分析基体的应力/应变状态,求解式(16)~式(18)中的εm(0,rm),由于基体尺寸要比光纤大得多,将基体看做无限大体,无限大空间轴对称基体边界条件为:
(20)
取双调和函数为
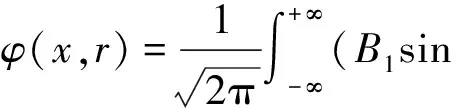
(21)
为保证r→∞时有界,贝塞尔函数I0(r)与I1(x)的系数为0,即:C1=C3=0;由于是空间轴对称结构,所以B2=0;进行标准化处理:B1=1;利用双调和函数(21)得到应力解为:
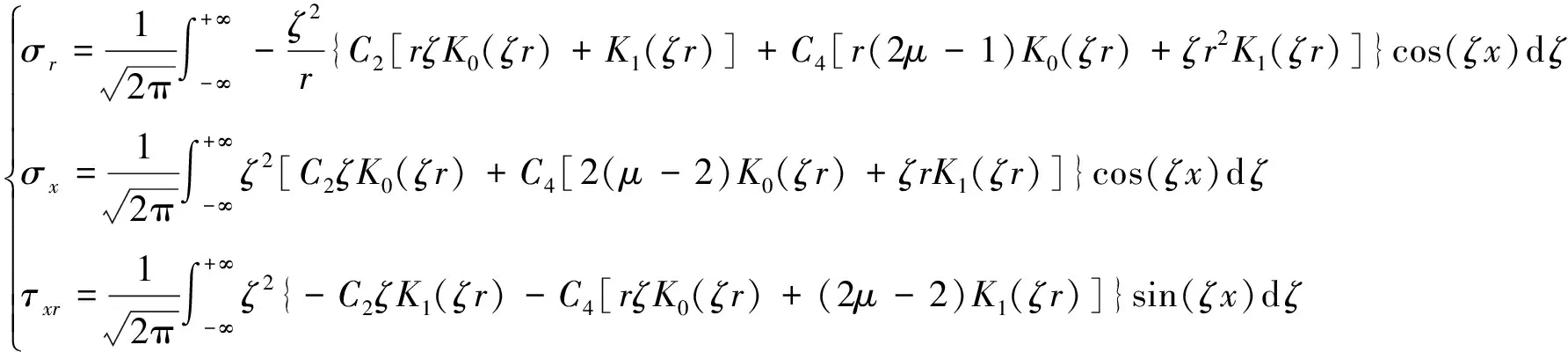
(22)
利用边界条件(20)得出:
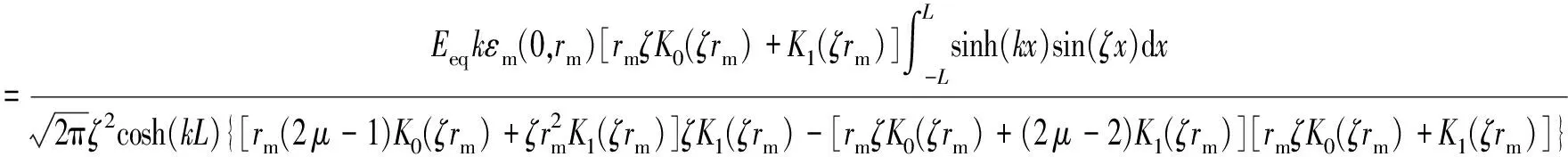
=V4εm(0,rm)
(23)
=V2εm(0,rm)
(24)
基体轴向应变表达式为
(25)
基体粘结中心区域的轴向应变值εm(0,rm)为
(26)
利用式(26)获得解析解仍比较困难,一般是将无限域转化为有限域,利用离散形式求其数值解,将式(26)转化为离散形式为
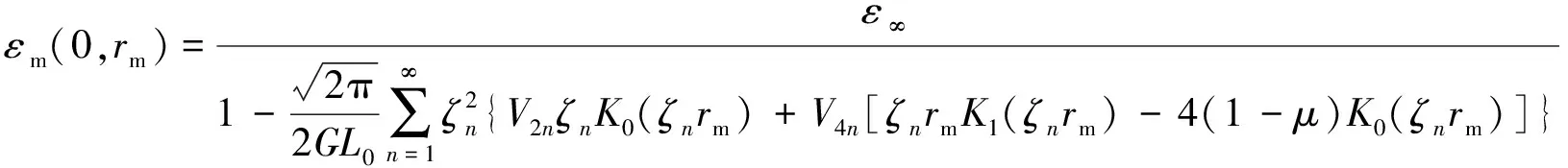
(27)
式中:L0为基体长度的一半;ζn=nπ/L0;n=1,2,3…。
将式(27)带入式(16)中,得到应变传递率表达式为
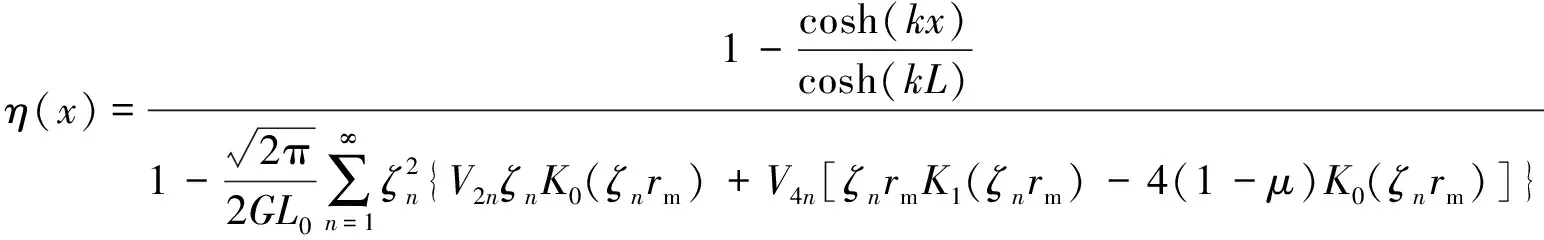
(28)
将式(27)带入式(17)中,得到平均应变传递率为
(29)
2 理论公式验证和参数分析
2.1 有限元验证
利用有限元软件Ansys Workbench对理论公式进行验证,由于结构的对称性,取一半进行分析。所使用材料物理参数如表1所示,其他参数为:rf=0.062 5 mm,rc=0.105 mm,rm=0.205 mm,R=10 mm,L=20 mm。图2为有限元模型图,采用六面体网格。

表1 材料参数
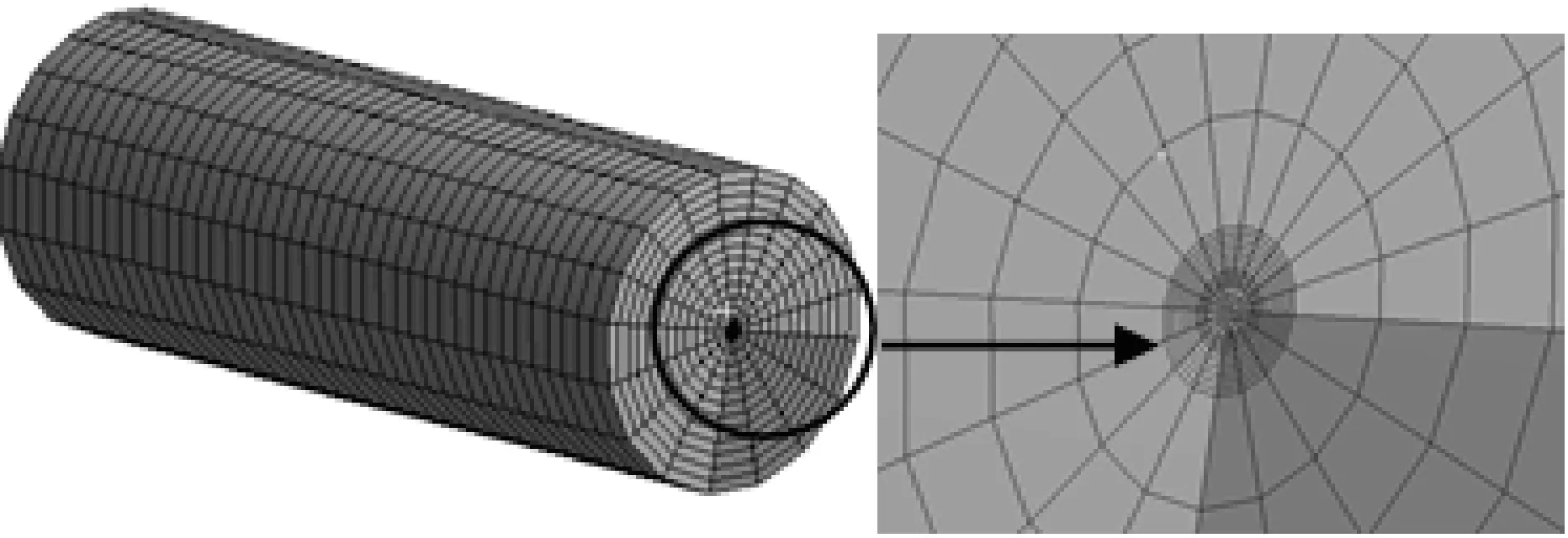
图2 有限元模型图
图3中为光纤应变对比图,FEM解是利用Ansys Workbench软件计算的结果,理论解1是利用本文应变传递理论公式得出的结果,理论解2是根据文献[8]中相关内容得到的计算结果。从图3中可以看出:应变传递率的分布趋势是中间最大,逐渐减小至两端,两端的应变传递率最小为0;理论解1、理论解2和FEM解分布趋势完全相同,但是理论解1与FEM的之间的误差要小一些,理论解1更接近FEM解,两者之间的误差在5%以内。该算例中基体弹性模量较小,FBG传感器的存在改变了基体应变状态,由于文中理论模型考虑了基体与FBG传感器之间的相互作用,因此具有更高的精度。
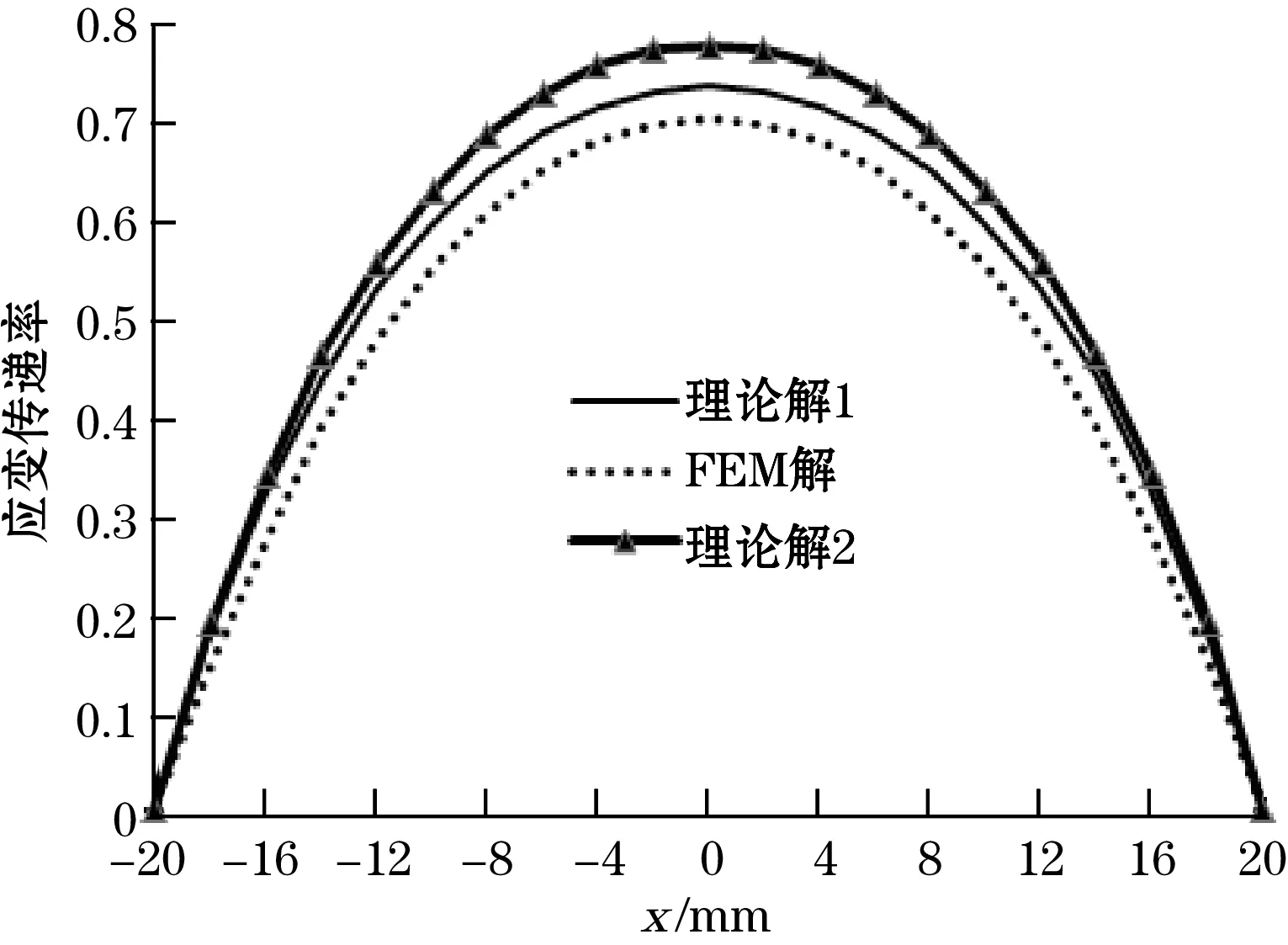
图3 有限元解与理论解的对比
2.2 参数分析
利用式(28)和式(29)进行参数分析,研究FBG传感器的结构参数对FBG传感器应变测量的影响,参数见表1。
图4和图5分别为基体弹性模量对应变传递率和平均应变传递率的影响。由图4可知,应变传递率随基体弹性模量的增大而逐渐增大。由图5可知,平均应变传递率随基体弹性模量和半粘结长度的增大而逐渐增大。当基体模量较低时,不仅是光纤与基体之间的中间层传递造成应变损失,而且FBG传感器的存在会改变基体局部结构,改变了基体应变状态,会进一步造成光纤应变偏小。因此,在低模量基体时,必须考虑基体与FBG传感器之间的耦合作用,利用本文理论对测量应变进行校正。

图4 基体弹性模量对应变传递率的影响
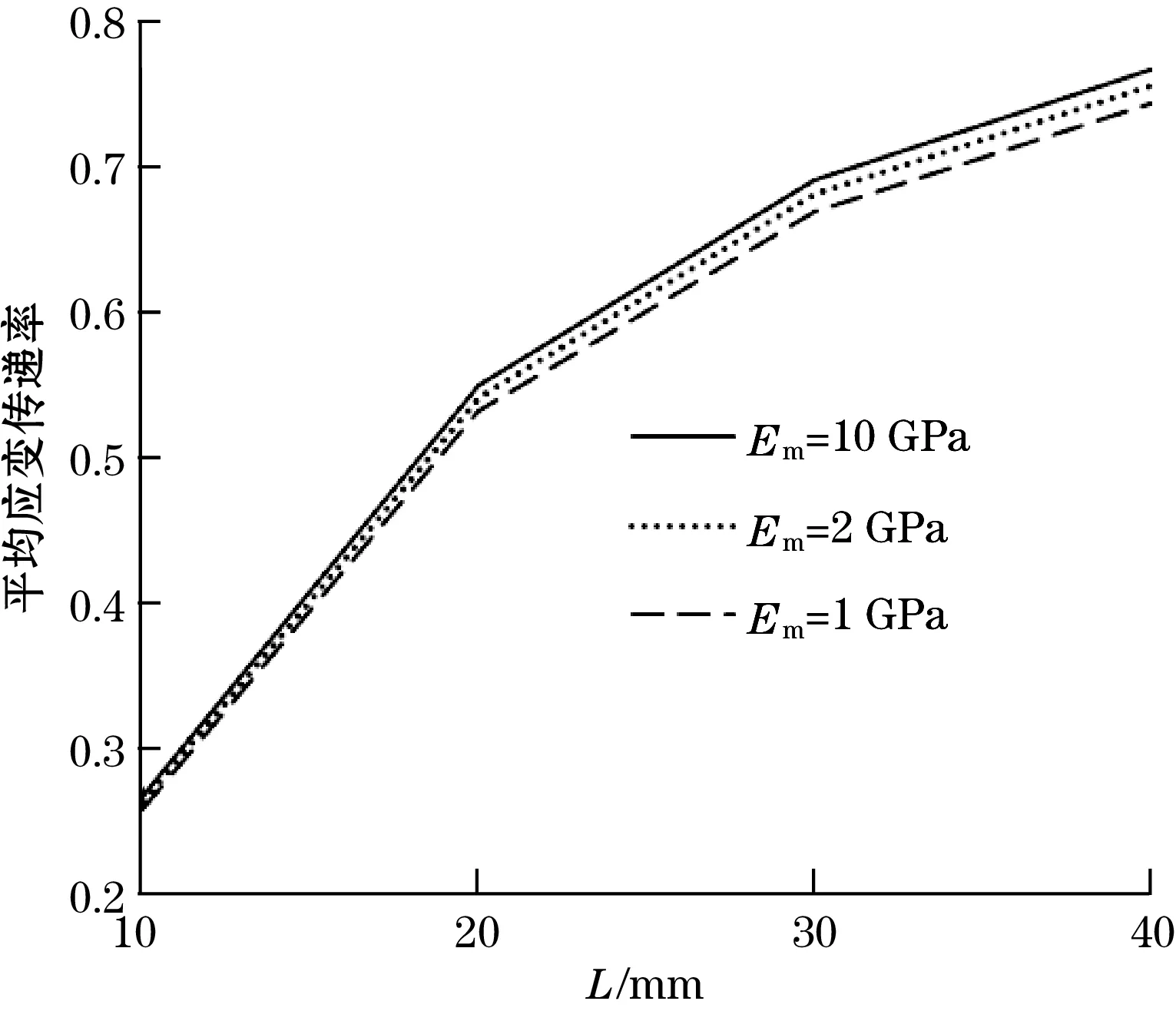
图5 基体弹性模量对平均应变传递率的影响
图6和图7分别为粘结层厚度对应变传递率和平均应变传递率的影响。由图6和图7可知,应变传递率和平均应变传递率均随着粘结层厚度的增加而逐渐减小,这主要是因为,随着粘结层变厚,会增加基体与光纤之间的应变传递损失。
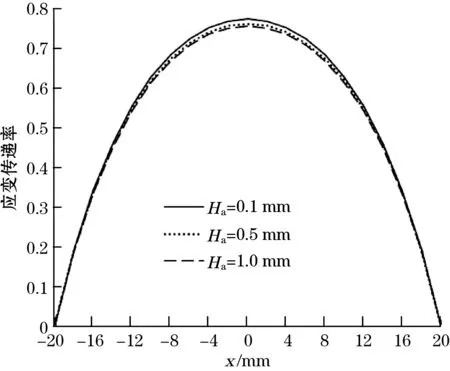
图6 粘结层厚度对应变传递率的影响
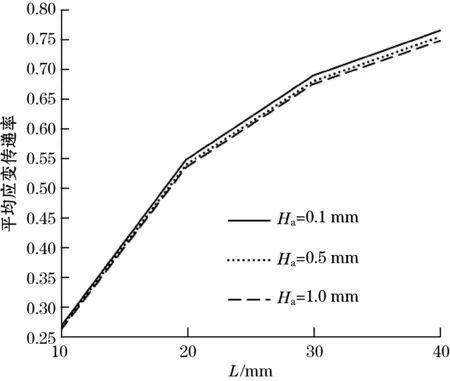
图7 粘结层厚度对平均应变传递率的影响
图8为半粘结长度为10 mm时FBG传感器各层结构的应变传递率曲线。由图8可知,粘结层的应变传递效果最好,其次是保护层,最后是光纤,即越靠近基体传递效果越好,因此在设计FBG传感器时,尽量减小保护层和粘结层的厚度,以提高FBG传感器的应变测量精度。
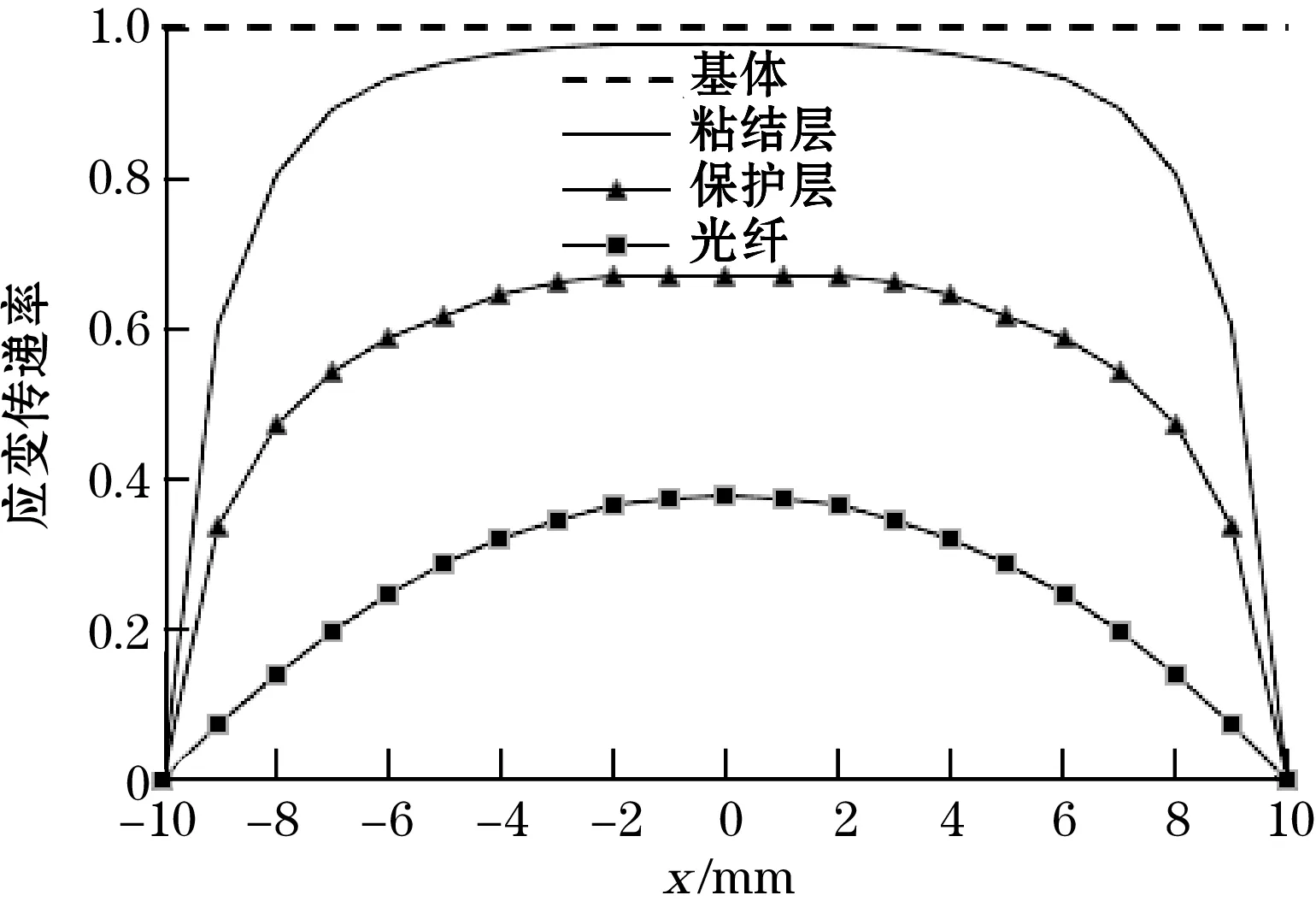
图8 FBG传感器各层结果应变传递效果对比
图9为半粘结长度为10 mm时,FBG传感器各层界面剪应力分布规律。由图9可知,剪应力关于FBG传感器中心呈奇函数分布,两侧剪应力最大逐渐到中心变为0,其中基体与粘结层之间的界面剪切应力最大,其次是粘结层与保护层之间的界面剪切应力,最小的是保护层与光纤之间的界面剪切应力。
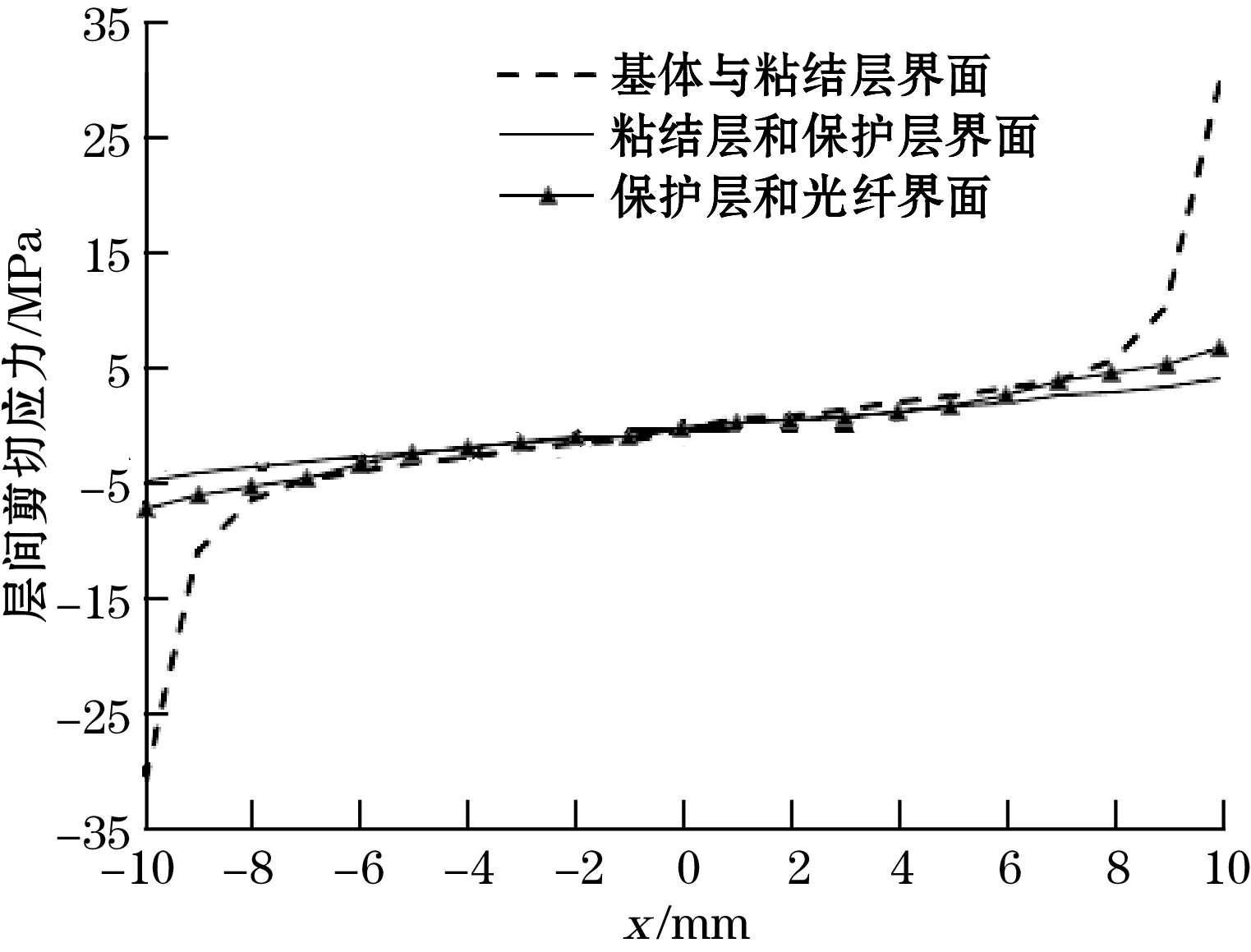
图9 FBG传感器层间剪切应力分布曲线
3 结论
本文利用弹性力学方法,对埋入低模量基体材料的FBG传感器应变传递问题进行了研究,得到以下结论:
(1)将基体结构看作空间轴对称结构来处理,基于傅里叶级数和贝塞尔函数,推导了基于双向耦合的埋入式FBG传感器应变传递理论公式,得出了光纤应变与基体预应变之间的关系,与现有相关文献中的内容有根本的区别。
(2)由于考虑了基体与FBG传感器之间的相互作用,文中应变传递理论模型具有更高的精度,特别是当基体弹性模量较小时。
(3)随着基体弹性模量的增加或粘结层厚度的减小,应变传递率和平均应变传递率都逐渐增大,因此,测量应变需要校正以提高测量精度,特别是在低模量基体时。
