基于时空转换原理的光栅莫尔信号数字细分
2021-09-07朱维斌
郑 罡,朱维斌,黄 垚,薛 梓
(1.中国计量大学计量测试工程学院,浙江杭州 310018;2.浙江大学现代光学仪器国家重点实验室,浙江杭州 310027;3.中国计量科学研究院,北京 100029)
0 引言
光栅作为一种常用的线角位移测量传感器件,广泛应用于精密工程、航空航天、光学、位移测量等领域,同时在计量标准装置研究领域也有着重要的地位。但受限于光栅刻线制作技术的限制,光栅本身分辨率有限,随着分辨率要求及动态测量性能的需求提高,传统光栅结构很难满足测量精度和速度的需求[1-2]。
在不改变光栅空间刻划线的前提下,想要获得更高的分辨率,需要在现有的基础上对光栅莫尔信号进行区间分割来实现莫尔信号的细分[3]。光栅莫尔信号的电子学细分方法具有细分倍数大、易于实现数字集成和动态测量的优点,得到了广泛的应用。近年来,随着单片机、DSP和FPGA在光栅处理上的应用,出现了许多高速快捷的电子细分方法,包括幅值细分、锁相倍频等细分方法都已实现了工程化,但这些方法大多数都是从空间的角度去测莫尔条纹的位移量[4]。基于莫尔信号空间信息的细分方法比较容易受到原始信号中直流量偏差、幅度偏差、正交偏差以及高次谐波和高斯白噪声的干扰而产生细分误差,因此对光栅莫尔信号质量要求较高。国内一些学者提出了基于时空转换原理的测量方法,借助一个匀速运动载体,把空间位置差(位移)表征为时间差再进行测量[5-7]。
本文基于时空转换原理开展莫尔信号数字细分方法研究,在FPGA平台上利用载波调制的方法将与位移相关的莫尔信号相位信息加载到时间信号上,通过时间信号频率的变化计算其周期变化值,从而得到包含位移信息的细分数,实现光栅莫尔信号的时空转换细分。
1 光栅系统测量原理
本文针对反射式圆光栅进行讨论,其光栅测量系统主要由主光栅、指示光栅、光源和光电元件组成,在测量过程中,主光栅与指示光栅相对移动形成莫尔条纹,由光电元件转换输出两路相差90°的正余弦电信号。测量系统如图1所示。
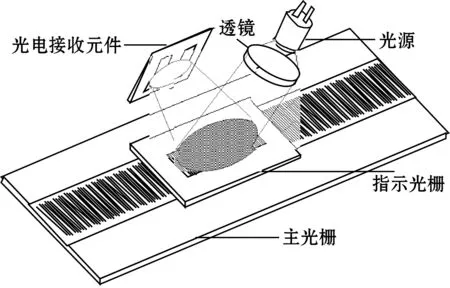
图1 光栅测量系统结构
两光栅相对运动产生的莫尔条纹被光电接收器接收后输出两路差分信号,称为莫尔信号。光栅每移动一个栅距W,产生一个周期的莫尔信号,因此可以通过对莫尔信号周期数的计量来判断光栅的实际位移。理想的光栅传感器输出的两路莫尔信号可以看作是正交的正、余弦信号:
(1)
式中:θ为光栅莫尔信号的相位值,θ=2πx/W;W为栅距;x为光栅位移;U为莫尔信号的电压幅值。
因此在一个栅距的范围内,莫尔信号相位θ是光栅位移的映射,可以根据莫尔信号的相位对输出进行数字细分,来提高光栅测量系统测量的分辨率,保证测量精度。
2 时空转换原理
在经典运动学中,物体空间位移Δx为其瞬时速度v(t)在时间上的积分:

(2)
在大多数的应用中无法获得所有时刻的瞬时速度,因此瞬时速度对于时间的积分并不能有效获得。借助时空域转换原理,将光栅莫尔信号位移量的测量转换为对时间的有效测量,可获得非恒定速度运动下光栅莫尔信号的位移量。
建立如图2所示的一对坐标系,静止坐标系s和运动坐标系s′,s相对s′以速度v0匀速移动,两者在初始状态下重合。假设质点P从运动坐标系s′ 的横坐标上的原点开始运动,其相对s运动的瞬时速度为v。如图2(a)所示,无论质点运动速度与方向如何,其经过静止坐标系上某一固定考察点的时间为T,此时质点相对于s′原点O′的位移为Δx′。

图2 双坐标系位移图
由于s′相对于静止坐标系s在做匀速运动,运动质点相对于s原点O的位移:
Δx=Δx′+v0T
(3)
如图2(b)所示,当s′坐标系继续移动到考察点处的时间为T′,可以得到O′相对于O的位移与Δx相等,结合式(2)可得T时刻质点P相对于s′原点O′的位移:
Δx′=v0(T′-T)=v0ΔT
(4)
由于v0是恒值,质点P相对于s′的位移可以转换为对时间差值ΔT的求取。
为了求取一段时间内P点的位移,在静止坐标系s上设立多个相同间隔L的考察点,如图3所示。

图3 设立多个考察点的双坐标系
记录P点通过第i个考察点的时间Ti,O′通过各个考察点的时间恒为T0,在P点经过第N个考察点后,其相对于O′的总位移x为各个考察点位移之和:
(5)
由于v0是恒值,因此对各参考点的P点与运动坐标系的时间测量即相当于对P点实际位移的测量。通过建立一对静止和运动的坐标系,可以将空间域上位移量的测量转换为对时间域上时间差值ΔT的测量,这是时空转换原理中通过时间测位移的思路。
3 光栅时空转换细分原理
本文采用一种载波相位调制的方法,产生周期为T0,正交的两路方波信号Es(t)和Ec(t):
(6)
式中ω0为方波信号角频率。
通过两路方波信号与两路莫尔信号分别相乘并相加,调制后的信号表示为
S=us(x)Ec(t)+uc(x)Es(t)
(7)
通过带通滤波滤除基波以及高次谐波成分,得到含有空间位移信号θ(x)的时间信号:
(8)
Up信号将光栅莫尔信号的相位转换为Up与载波信号Es(t)的相位差,因此将载波信号Es(t)作为运动坐标系,每经过Es(t)的一个周期设立考察点,则光栅莫尔信号就相当于在Es(t)坐标系上运动的质点P,根据时空转换原理,第i个考察点处莫尔信号的相位差为
Δθi=ω0(T0-Ti)
(9)
经过N个考察点后光栅莫尔信号的相位θ(x)为
(10)
由于θ=2πx/W,所以光栅的总位移为
(11)

通过上述时空转换方法,将光栅位移的测量转换为对调制信号周期的测量。只需测量一定周期数内调制信号的各个周期T1~TN,即可得到光栅的空间位移,测量分辨力取决于时间量测量的分辨力,因此该时空转换细分方法的细分数不是确定值,而取决于一个载波周期通过的时间计数脉冲的最大值。细分辨向的原理如图4所示。

图4 细分辨向原理
由式(11)可知,光栅的辨向功能可以通过Ti的大小判断。当Ti
4 光栅时空转换细分原理
本文的数字电路在FPGA平台设计完成。整个细分电路的原理框图如图5所示。
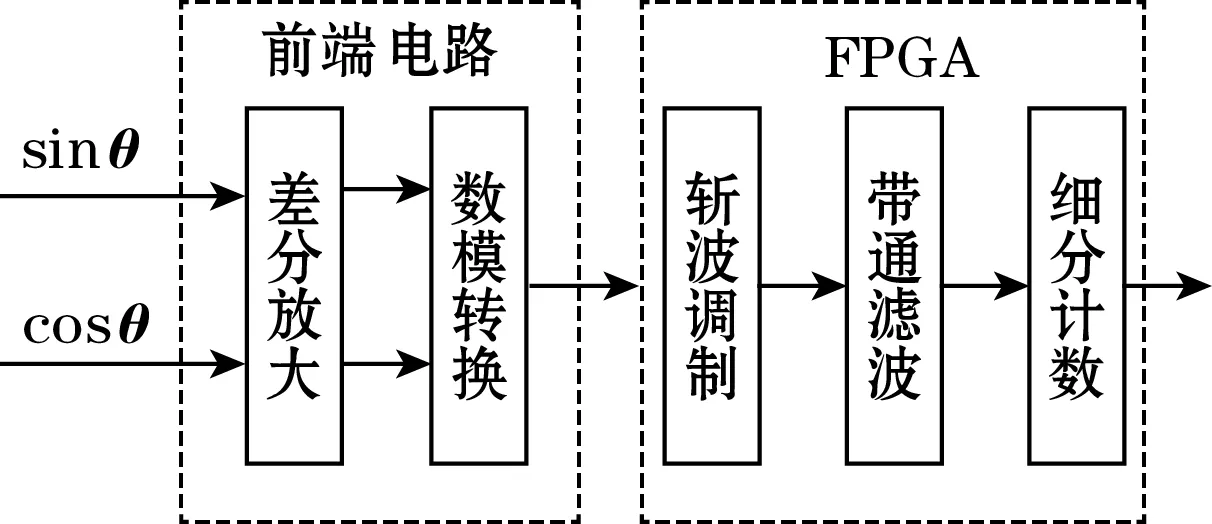
图5 细分电路原理框图
光栅输出莫尔信号的形式为差分正弦信号,频率范围为0~20 kHz。因此在电路的前端信号调理部分采用差分运放放大微弱莫尔电信号,经过40 MSPS采样率的高速差分ADC接收,在尽可能保留模拟信号信息的前提下转换为数字信号,供后续细分电路使用。
4.1 载波调制模块
载波调制模块通过正交信号的运算得到调制后信号,其在FPGA数字电路中包含乘法器、加法器、PLL与载波模块部分,其结构框图如图6所示。

图6 调制模块
为了实现光栅莫尔信号的载波调制,需要生成两路相位差90°的方波作为载波。PLL根据FPGA的系统时钟分频出一个频率2 MHz的时钟信号,然后通过上升沿和下降沿来转换成两路频率为1 MHz相位差90°的方波信号,如图7所示。

图7 载波生成过程
将采集到的光栅莫尔信号与载波信号相乘相加得到调制后的信号。
4.2 带通滤波模块
为了有效从载波调制后的信号中提取出含有空间位移信号θ(x)的一次谐波信号Up,需要滤除调制信号S中的基波成分和高次谐波成分,因此采用FIR数字带通滤波器进行滤波。
考虑到本文调制后Up信号的频率范围在1 MHz附近,ADC采样率为40 MSPS,设计一个采样率40 MHz,通带范围在800~1 200 kHz的数字带通滤波器,以消除基波成分和高次谐波成分。
为了使实际数字滤波器更接近理想滤波器,需要提高滤波器的阶数,各阶数下的滤波器幅频响应曲线如图8所示。

图8 各阶数下的滤波器幅频响应曲线
随着阶数的增加,数字滤波器的特性会更加接近理想滤波器,但过大的阶数会带来较大的信号延时以及大量的资源占用,因此综合考虑采用256阶的FIR带通数字滤波来滤除基波和高次谐波成分。
通过与ADC采样率对应的40 MHz系统时钟对Up和载波信号周期计数并做差后得到当前莫尔信号周期的细分倍数M,M等于系统时钟与载波信号的比值,即M=40 MHz/1 MHz,即40倍细分。
5 光栅时空转换细分原理
本文提出的时空转换细分方法针对16384刻线的高精度圆光栅实现40倍细分,细分分辨率为1.977″。为了验证本文所提的时空转换细分的有效性,开展两组实验:仿真方法评估细分结果的线性度;电路测试方法验证细分结果稳定性。
5.1 细分功能验证
在本实验中,通过MATLAB生成两路10 kHz的正交信号来模拟理想光栅莫尔信号,将生成的两路正弦信号进行时空转换细分,以实现信号相位的40倍细分,采用Modelsim观测其仿真结果如图9 所示。对于10个周期的理想正弦莫尔信号,得到细分数为400,实现了莫尔信号周期的40倍细分。

图9 莫尔信号细分仿真结果
对细分结果进行评估,计算其在一个理想莫尔信号周期内的误差如图10所示。细分误差小于±1.3″,即细分数的偏差不会超过一个细分值,确保细分功能的正常。

图10 理想细分角度误差
5.2 细分结果比对
在机械转台上进行实验测试,转台内圆光栅总共16384刻线,平均每刻线表示角度为79.1″。实验所用基准装置为M3000系列光电读数头,该读数头可以实现光栅莫尔信号的1 024倍细分,细分分辨率达到0.077″。
在自制电路板中实现本文提出的细分方法。自制电路采用Altera Cyclone IV系列(EP4CE115F29C7)芯片,配置12 bit 40 MSPS的并行A/D用于采集转台输出的光栅莫尔信号用于数字细分。整个实验过程中实验装置的搭建如图11所示。

图11 实验装置图
首先验证细分结果的封闭性,通过圆光栅自带的零位信号作为标志记录下经过转台正周期的细分数结果,见表1。

表1 转台正周期细分结果
可以看到,转台每旋转1圈,时空转换细分电路输出655 360个细分脉冲,与M3000读数头的1 024细分结果比值恒为25.6,实现了光栅莫尔信号的40倍细分。
在转台光栅莫尔信号的2个周期内对时空转换细分进行标定,结果如图12所示。

图12 细分误差标定结果
可以看到基于时空转换的细分方法对莫尔信号的细分误差在±1.5″以内,与图10的结果基本一致。
基于时空转换原理的细分方法在16384刻线的圆光栅转台应用中可以实现莫尔信号的40倍细分,其细分的误差在±1.5″内。
6 结论
本文借助时空转换原理,将其用于光栅莫尔信号细分方法,通过载波调制将莫尔信号的空间位移信息转移到时间调制信号上,通过周期测量来实现莫尔信号的相位细分,并通过数字电路实现该细分功能,具有可靠性高、易于集成以及成本低等特点。在动、静态测量中实现了光栅莫尔信号的40倍细分,并通过仿真验证了细分电路的功能,在16384刻线的圆光栅进行实验,细分的分辨率为1.977″,细分误差在±1.5″以内。
