基于SROPL的金属管道损伤谐波检测方法研究

赵以振，王新华，杨 林，段 宇，王 昌

(北京工业大学机械工程与应用电子技术学院，北京 100124)

0 引言

目前，管道内检测技术能够对重特大管线损伤实现有效检测，但过弯道时容易阻塞并且成本极其昂贵[1-2]。管道外检测技术中瞬变电磁法能够检测壁厚减薄、管体裂纹等缺陷，但其信号存在衰减及不连续等问题[3]；地磁检测法基于环境磁场对管道实现被动式损伤检测，但检测信号非常微弱，极易受外界干扰[4]；涡流检测法通过主动施加激励信号的方式增强检测效果，但受趋肤效应限制明显[5]。此外，实际检测过程中探头的晃动、环境的噪声等都会降低管道损伤目标的辨识度，需要采用恰当的信号处理算法进行提取。Q. Song利用小波变换对磁场分量进行分解与重构，识别出高压管道的裂纹缺陷[6]。Y. Huang采用EMD算法对铝合金焊缝中的气孔缺陷进行识别[7]。J. Bosse设计了传感器阵列，采用MUSIC算法确定目标信号源，实现了对平面金属结构中的损伤识别[8]。区别于传统滤波方法，C. B. Wan采用双稳态SR方法转移噪声能量，实现了对磁异常目标信号的提取[9]。

本文提出一种谐波检测方法，激励信号同时具备多种频率成分，并采用高灵敏度隧道磁阻(TMR)矢量传感器阵列对回波信号并行采集。针对管道损伤处信号异常特征，采用变尺度自适应时域随机共振(SR)增强目标信号能量，并通过量子遗传算法(QGA)对系统模型的参数寻优，以实现噪声、系统、信号的最佳协同。利用正交锁相微弱信号放大作用，消除背景激励场，将各矢量分量进行阵列融合实现对管体损伤的识别。

1 谐波检测原理

谐波检测是一种基于调频载波谐振原理的金属管道损伤非接触式电磁无损检测方法。谐波激励信号具备高频和超低频电磁波特性，能够在提高检测灵敏度与分辨率的同时克服金属管壁的趋肤效应限制，实现在役铁磁性管道管体表面或亚表面的损伤检测。谐波信号模型可表示为

(1)

式中：i为谐波分量合成个数；Ai为幅值分量；fi为频率分量；θi为初始相位。

管体损伤在不同谐波成分激励下会呈现局部信号异常，根据其矢量特征对管道径向、轴向和周向三维信号采集，从而提取和辨识损伤源位置。检测原理如图1所示。

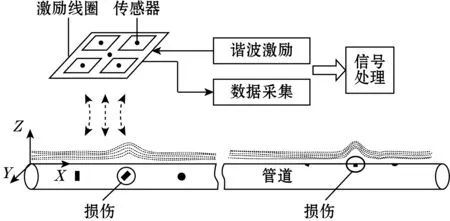
图1 谐波检测原理

2 损伤目标辨识算法

实际管道检测过程工况复杂多变、干扰因素多，尽管谐波检测能够在一定程度上屏蔽环境噪声，但目标信号多以非线性、非平稳、低信噪比的形式存在，导致目标信号被淹没，为损伤信号的有效辨识带来不便。

2.1 变尺度时域随机共振

随机共振信号处理方法基于能量转移机制，将噪声能量转移到目标信号中并产生随机共振谱峰，适用于强噪声背景条件下微弱目标信号的特征提取和检测[10]。经典非线性双稳态郎之万模型可表示为：

(2)

式中：x(t)为系统输出信号；s(t)为输入信号；n(t)为噪声；U(x)为势函数；a和b为非负系统参数调节势阱宽度和势垒高度。

随机共振系统作用的前提条件之一是满足绝热近似理论的小参数信号特征，而实际谐波检测信号属于宽频大参数信号。因此，对采集信号进行频域线性尺度压缩，调制到小参数范围内并采用四阶龙格库塔方法对共振系统解算[11]，其表达式为：

(3)

式中：xn为第n个数据点；a和b为非负系统参数；h为变尺度积分步长；sn为含有噪声的实际信号。

随机共振系统处理后的信号在时域会发生畸变，而管道损伤目标信号辨识更侧重于时域信号。故引入恢复系统对时域信号还原，将函数对时间求一阶导数，可表示为

r(x)=-ax+bx3

(4)

2.2 量子遗传算法

为实现随机共振系统的理想输出状态，采用量子遗传算法对双稳态随机共振系统参数a、b和尺度参数h寻优。将量子态引入到遗传编码中，利用量子门的旋转策略实现进化和更新，规避了人工选择参数误差大的缺点，以更小的种群规模和更短的寻优时间实现参数最优解[12]，步骤如下：

(1)确定随机共振系统参数与尺度的寻优区间，设置种群规模、最大遗传代数与二进制量子编码长度；

(3)计算种群中个体的概率幅，观测量子态并进行适应度计算，将最优适应度解的染色体保留，并作为下次循环的初始群；

(4)将信噪比(SNR)作为适应度评价函数，可表示为

SNR=10lg(Ps/Pn)

(5)

式中：SNR单位为dB；Ps和Pn分别为信号和噪声的有效功率。

(5)判断当前最优解是否符合终止条件，若是则退出算法并输出当前解，若否则继续执行下一步；

(6)采用量子旋转门更新策略对遗传代进化并更新，返回步骤(3)重复执行。

2.3 正交锁相(OPL)阵列融合

谐波检测带来优势的同时，会引入激励信号场。根据电磁检测原理，采集信号中不会引入激励信号以外的其他频率成分，因此固定可控。采用相关性检测原理能够有效抑制激励背景场，从而提取损伤信号，原理如图2所示。

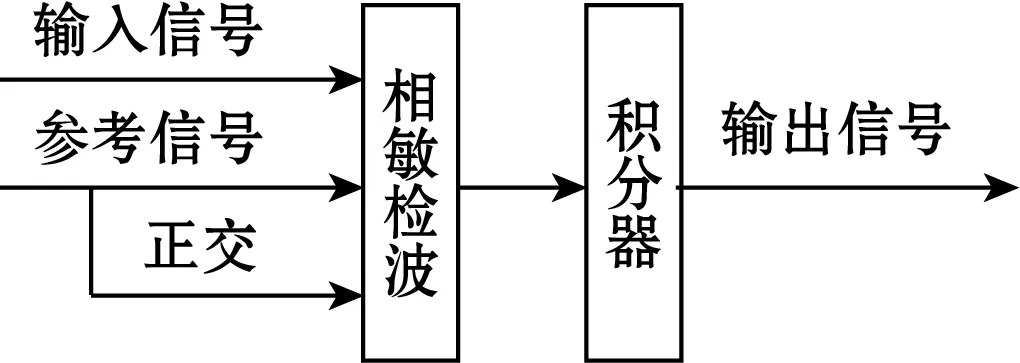
图2 正交锁相原理图

正交锁相的核心是相敏检波和积分器，分别由模拟乘法器和低通滤波器实现[13]。假设输入谐波信号为

S(t)=Asin(ω0t+φ)+Bsin(ω1t+φ)+N(t)

(6)

参考信号为

R(t)=Csin(ω2t+φ+θ)

(7)

式中：A、B、C为幅值；φ为初始相位；ω为角频率；N(t)为模拟噪声；θ为参考信号与谐波信号的相位差。

在实际检测信号相位角未知的条件下，采用正交方法消除相位差的影响。将输入信号与参考信号相乘得到输出信号V(t)，同时将参考信号自身正交后的R⊥(t)再次与输入信号相乘得到正交输出信号V⊥(t)，表示为：

(8)

解调后的信号中包含直流信号项、差频信号项和倍频信号项。当ω0=ω2时，采用低通滤波器并设置恰当的截止频率，可化简为

(9)

同理，当ω1=ω2时，可得B·C项。

谐波磁场作为空间连续矢量场，采用张量模阵列融合方法，发挥矢量传感器阵列优势，进一步消除空间信号姿态带来的误差[14-15]。假设谐波磁场H=[Hx,Hy,Hz]，其全张量G表示为

(10)

将传感器各轴矢量信号融合得出张量G模量的极大值，从而对异常信号边界进行确定，能够更直观表征管道损伤目标信号Starget：

(11)

3 仿真分析

为验证谐波检测管道损伤识别算法的有效性，采用经典磁偶极子理论与调频载波理论构建信号模型，表示为

(12)

式中：μ0为真空磁导率；M为磁偶极子量级大小的磁矩；r为原点到检测点的矢径；r=|r|；Ai、fi、θi分别为谐波分量的幅值、频率、初始相位；n(t)为噪声。

仿真时，设计两处磁偶极子损伤源信号模拟实际管道缺陷位置，垂直检测高度1 m，水平检测长度5 m，矢量磁矩[277，-29，726]A·m2，谐波分量1的幅值2、频率23 Hz、初始相位0，谐波分量2的幅值3、频率1 000 Hz、初始相位0，加入的噪声SNR=2 dB。检测阵列中心探头采集的数据归一化后如图3所示，可以看出损伤目标被完全淹没，不能直接识别。

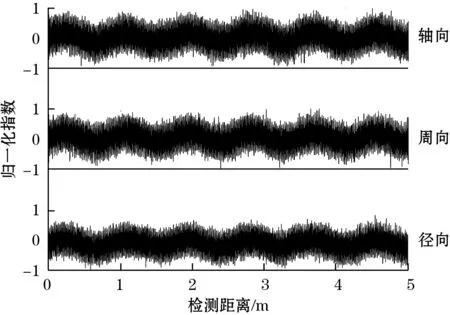
图3 仿真检测数据

由于仿真采样频率高，先采用四阶巴特沃斯低通滤波对信号选频，截止频率fs为5 000 Hz。采用量子遗传算法对随机共振系统参数寻优，并采用SNR作为适应度函数，各参数区间分别设置为a(0,10]，b[10,20]，h×fs[5 000,10 000]。设置最大遗传代数30，种群大小50，染色体长度20，系统输出最优解如表1所示。

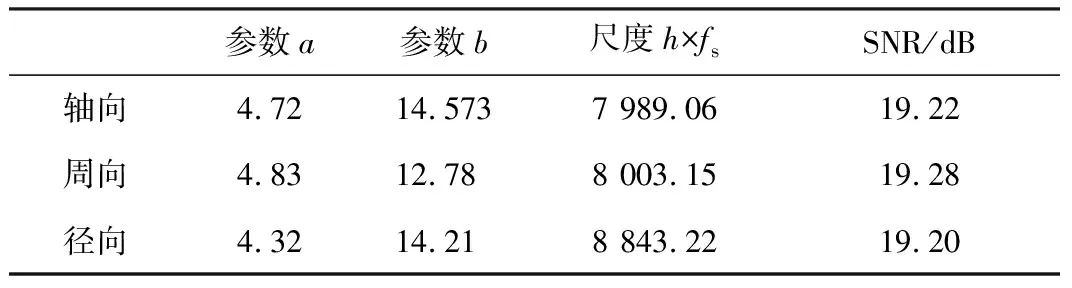
表1 随机共振最优解

通过该算法处理，信号SNR提高了9.6倍。以阵列中心传感器径向信号为例，时域恢复后如图4所示。

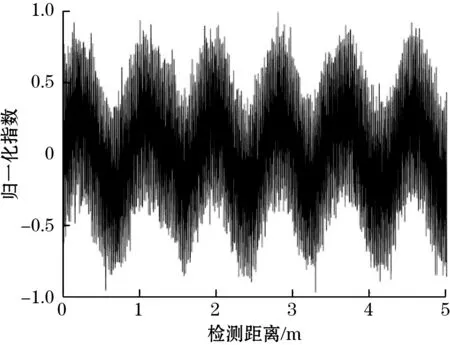
图4 中心传感器径向信号

采用正交锁相信号处理方法将激励信号固有频率消除，参考信号设置为

(13)

式中：fj=1，2分别对应谐波激励信号中的高频和低频。

以阵列中心传感器的三轴信号为研究对象，为保证算法完备性，将同频参考信号的高频成分和低频成分分别与采集信号的每个维度进行相敏检波，将参考信号各自平移π/2后再次与采集信号相敏检波，积分器截止频率均为15 Hz，结果如图5所示。

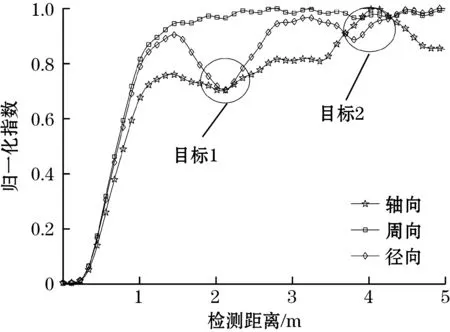
图5 损伤目标识别

从图5可以看出，轴向和径向信号相对于周向信号更加明显，但不同损伤信号的敏感方向有所区别，会导致目标判别不直观。因此，将矢量探头阵列数据进行张量模量融合，对目标信号进行了有效提取，如图6所示。

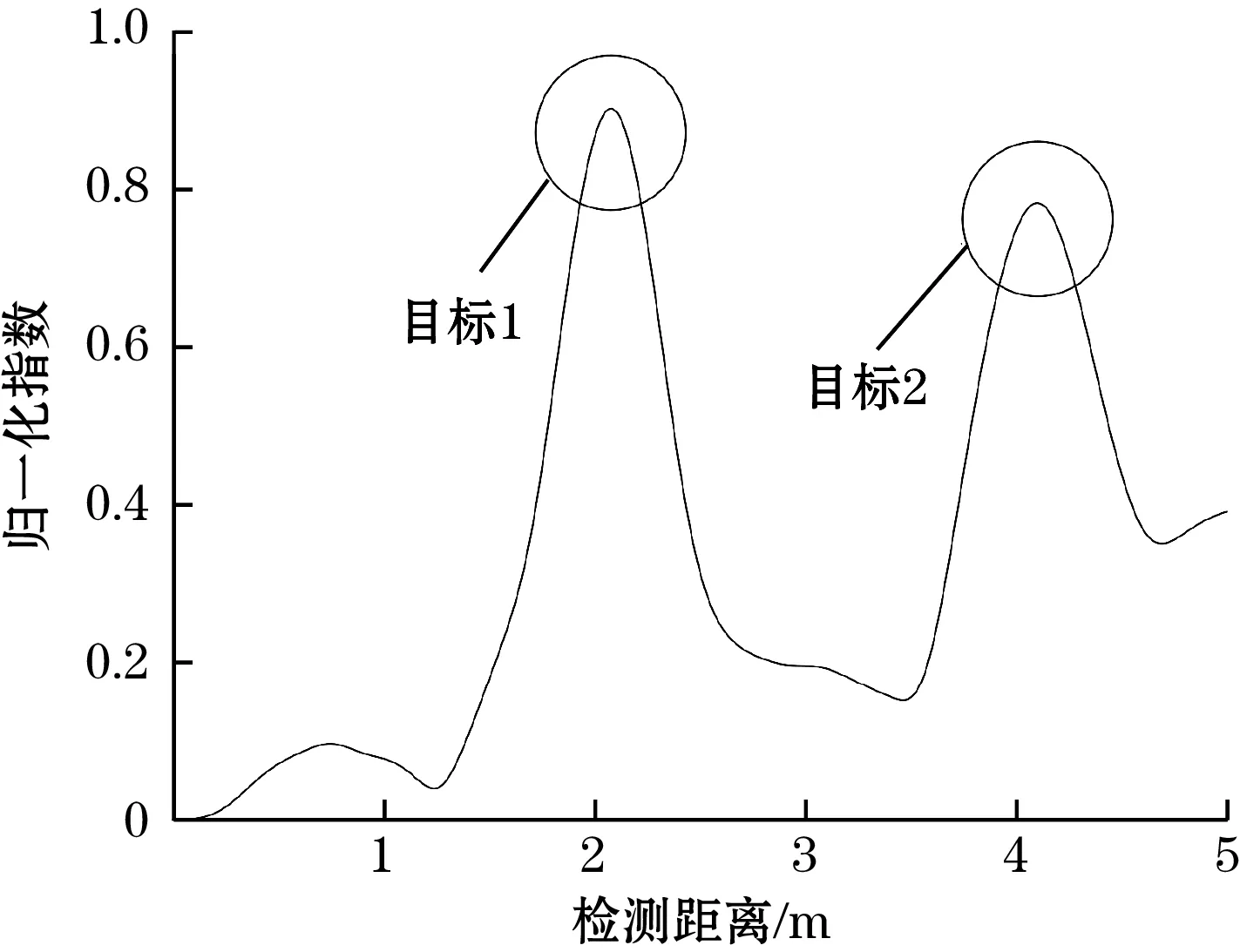
图6 张量模量阵列融合

此外，通过仿真研究发现，算法有效性与SNR有直接关系。当SNR≤5 dB时，目标信号混叠严重，算法失效；随着信噪比提高，当SNR≥20 dB时，目标信号能够有效辨识，如图7所示。在前述的谐波检测管道损伤仿真模型中，采用量子遗传随机共振算法将SNR=2 dB提升至SNR>19 dB，再利用正交锁相张量模量阵列融合算法实现了损伤目标信号的提取，验证了算法有效性。

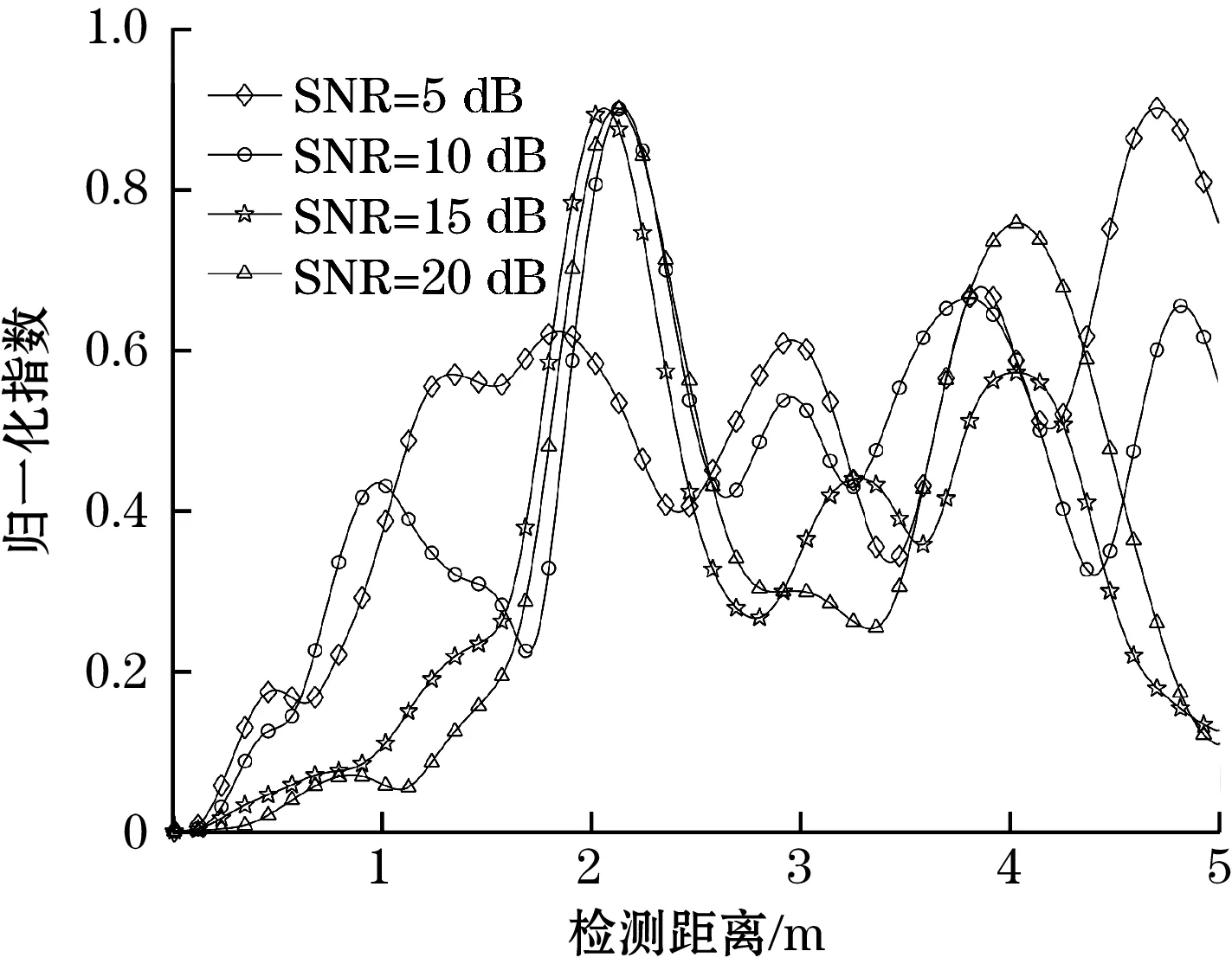
图7 算法有效性对比

4 实验

4.1 检测平台

为检验管道损伤谐波检测方法的有效性，搭建室内实验平台。选用Q235无缝钢管并预制模拟损伤，总长265 cm，外径7.5 cm，壁厚0.5 cm。设计5阵元TMR三维矢量传感器阵列，每轴信号以差分形式输出，并行采样频率为6 000 Hz。激励源输出谐波分量设置为低频23 Hz和高频1 000 Hz，激励电流为2.5 A。检测过程中传感器至管道上方的提离距离为28 cm，保持0.5 m/s速度匀速检测。实验平台如图8所示。

图8 实验平台

4.2 结果分析

5元矢量阵列检测数据共15组，将中心传感器三维数据作为对照，其余数据进行阵列融合。经多次实验，检测管段所得阵列中心传感器的最优原始信号如图9(a)所示。以其径向信号为研究对象，计算其频谱如图9(b)所示，为后续参考信号的设置提供频率依据。此外，从图9(b)中可以看出，除激励信号固有频率外，检测数据没有产生新的频率信息。

(a) 原始信号

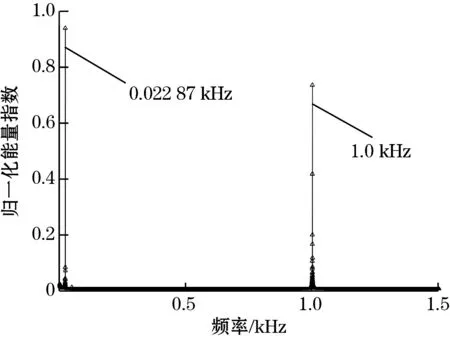
(b) 信号频谱图9 实验信号处理

截取管段中间部分的实验数据进行分析，共包含3处预制损伤，依次为轴向裂纹、周向刻槽和圆孔。首先将探头数据进行4 kHz低通滤波和归一化处理，消除传感器间固有偏置带来的差异性；然后采用量子遗传随机共振算法对目标信号增强，提升采集数据的SNR；最后采用正交锁相张量阵列融合的方法实现对目标信号的有效辨识，信号处理算法流程如图10所示。

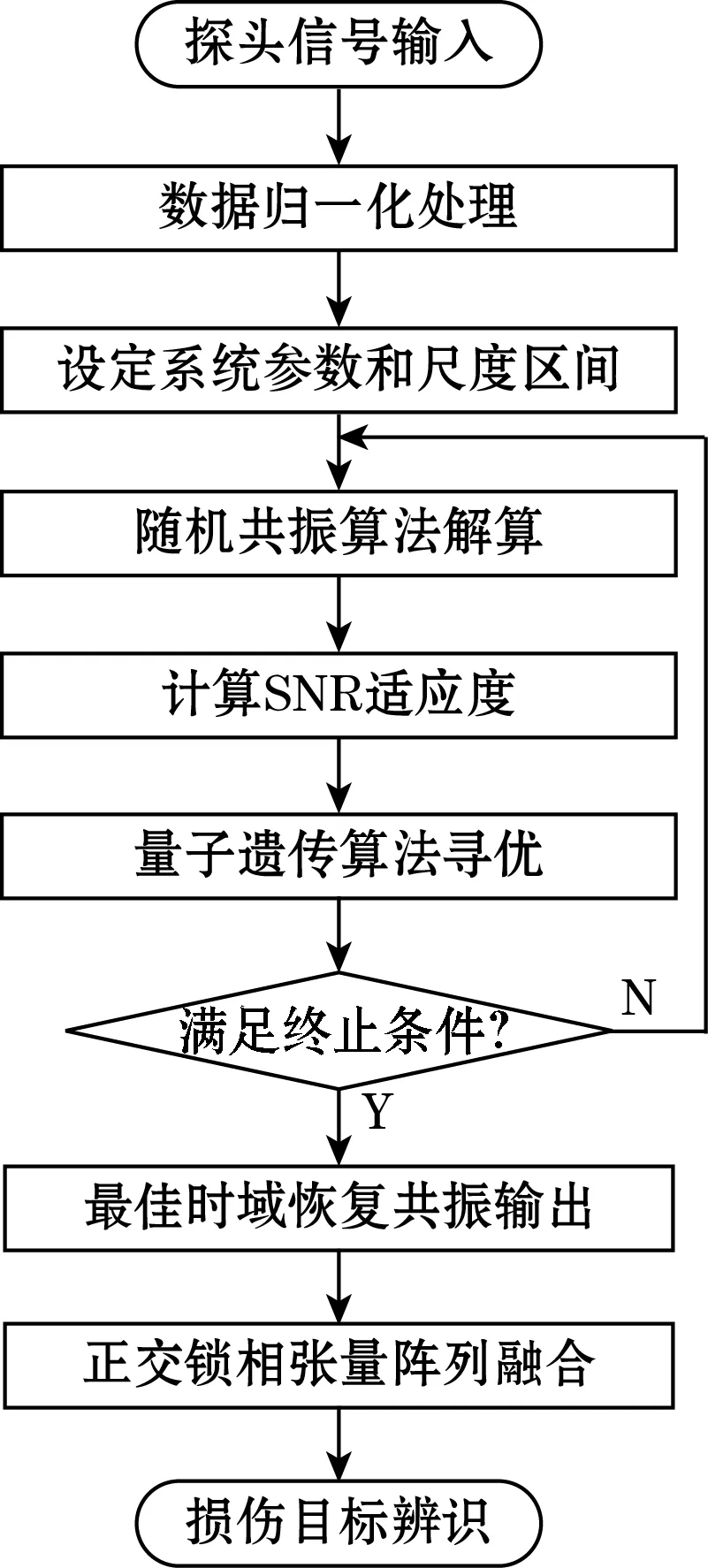
图10 信号处理流程图

实际信号处理结果如图11(a)所示，以其极大值作为损伤目标辨识依据，图中共有3处波峰从左至右依次对应图11(b)中的1#、2#、3#管道损伤类型。

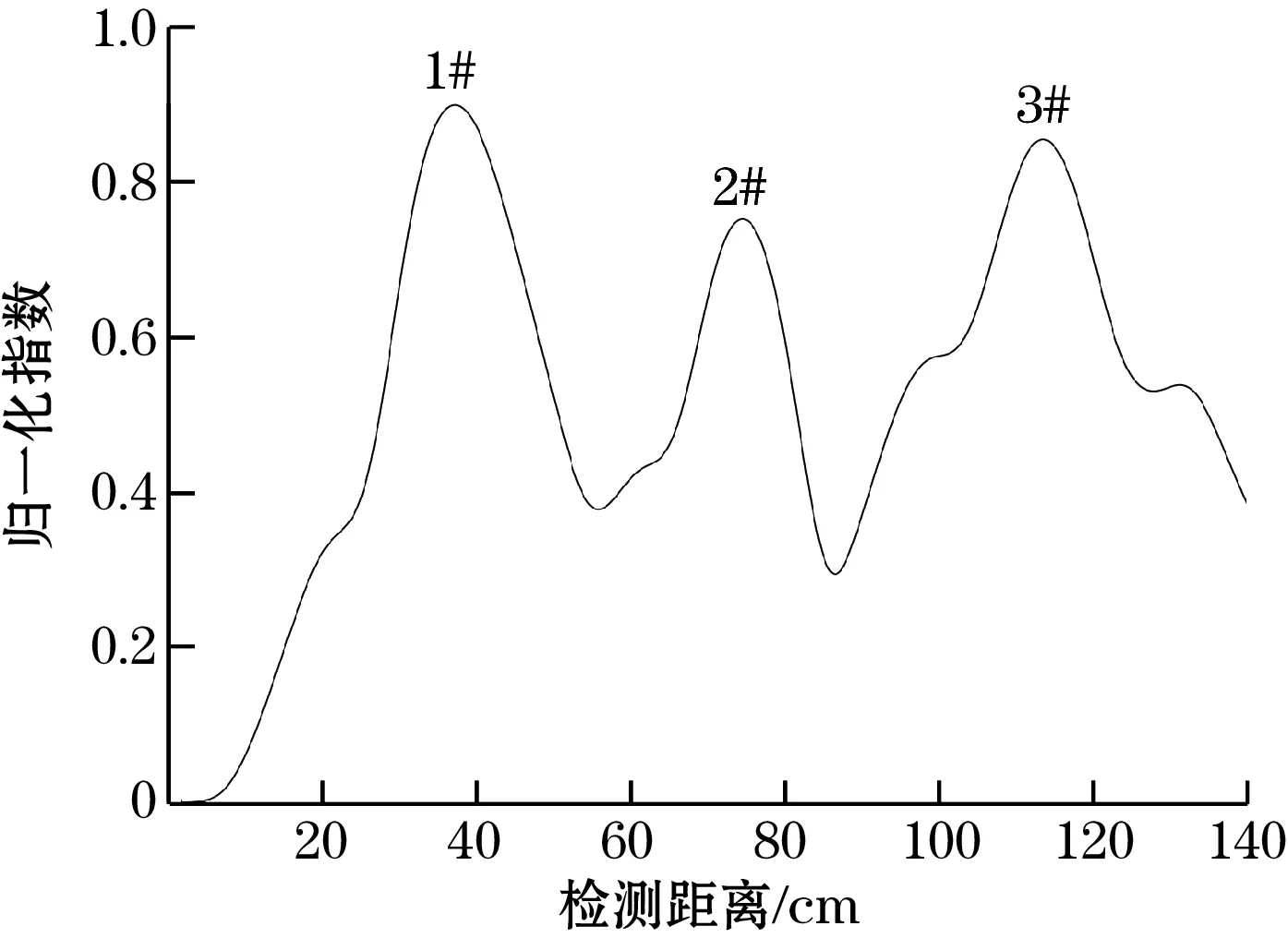
(a)处理结果

(b)损伤类型图11 实际管道损伤类型及处理结果

5 结论

本文提出一种金属管道损伤谐波检测方法，系统中采用调频载波合成激励信号、矢量传感器阵列采集回波信号，引入了变尺度随机共振、量子遗传算法和正交锁相阵列融合。该方法能够准确辨识管道损伤目标，并通过仿真与实验验证了其有效性，可为金属构件损伤提供一种非接触式电磁无损检测方法。研究中还发现，在信噪比低和损伤位置间隔小的工况下，会造成目标信号混叠，将在提升系统和算法分辨率方面继续研究。