双艉鳍船型的参数化建模及线型优化
2021-09-07张琪姜栋张明樊涛
张 琪 姜 栋 张 明 樊 涛
(1.南京天洑软件有限公司 南京 211100;2. 江南造船(集团)有限责任公司 上海 201913)
引 言
由于船舶主机的大部分能量用于克服航行过程中流体(水和空气)所产生的阻力,因此最有效的节能技术就是通过船型的设计优化尽可能降低船舶航行的阻力,并通过改善伴流的均匀性、提高螺旋桨的效率。
随着计算机技术的高速发展,CFD仿真技术也越来越多地应用在船舶的快速性预报领域,如赵丙乾等基于CFD软件对某双艉客船的航行阻力进行计算,阻力预报误差基本在3%以内,并探讨船舶第1层网格节点高度、船舶航速以及附体对计算结果的影响;Kwang-LeolJeong等基于径向基函数法(RBF)的网格变形方法,对日本散货船(JBC)船首形状进行改变,并通过CFD方法预报网格变形前后的阻力,进而得到阻力最优船型。
船型的参数化建模作为现代化的船型设计手段逐渐被广泛应用。将参数化建模技术与CFD仿真技术相结合进行阻力性能优化是目前最常用的船型优化方法。除阻力性能的优化外,近来船尾线型对伴流场的影响也受到更多关注,本文以某双艉鳍集装箱船为研究对象,基于CAESES软件建立了参数化的三维模型,并对其双艉鳍的线型进行优化,以期获得静水阻力及伴流均匀度俱佳的船型。
1 数值计算
1.1 数值计算方法
CFD数值模拟中常用的湍流模型中,标准k
-ε
模型适用于高雷诺数的湍流,它在模拟旋流和绕流的时候有缺陷。标准的k
-ω
二方程湍流模型包含了低雷诺数的影响、可压缩性影响和剪切流扩散,适用于尾迹流动、混合层和射流等的计算。SSTk
-ω
湍流模型则是同时具备k
-ω
模型在近壁区域的计算以及k
-ε
模型在远流场计算的优点,同时在湍流粘度定义中考虑了剪切应力的输运过程,可以精准地计算出逆向压力梯度引起的流动分离位置和作用区域,适用性更广。本文中的数值计算采用RANS模型框架下的SSTk
-ω
模型,SSTk
-ω
模型中k
和ω
的输运方程分别为: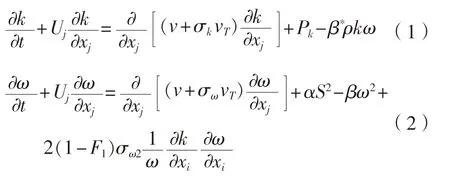
1.2 计算域及边界条件
考虑到船体是左右对称的,因此计算半船即可,该船在模型尺度(缩尺比36)下开展仿真计算,且为正浮的固定模型。以船体中线面上艉柱与基线的交点为原点,计算域在各坐标轴的范围(x
沿船长方向,y
沿船宽方向,z
沿高度方向)为:-2.0L
≤x
≤2.5L
,0≤y
≤1.2L
和 -1.0L
≤z
≤0.6L
,如图1所示,表1所列为边界条件的设置情况。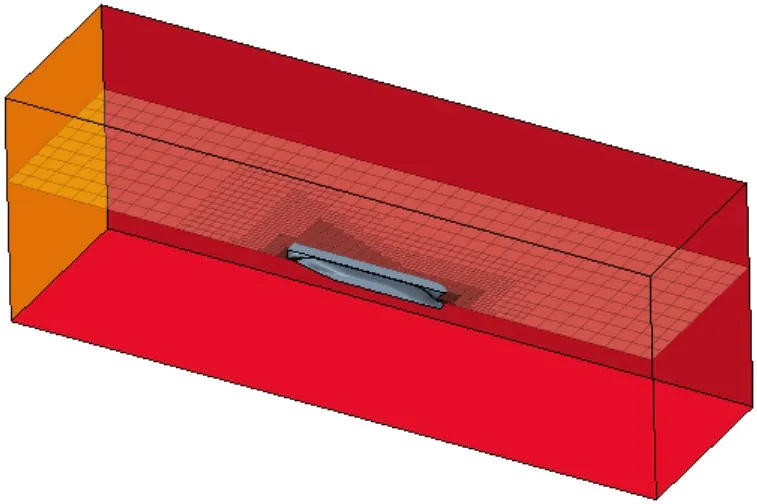
图1 计算域

表1 边界条件
1.3 网格划分
边界层网格应用棱柱形边界层捕捉且基于Two-Layer AllY
+壁面处理,第一层边界层厚度为1.8 mm,网格层数6,网格总数130万,船体表面的Y
+分布情况如图2所示。
图2 船体表面Y+分布
1.4 伴流场均匀度的评估
由于评估伴流均匀度的BSRA五项衡准使用起来考虑的因素较多,且判断起来较为繁琐,因此越来越多的学者倾向采用荷兰MARIN水池提出的WOF
(伴流目标函数)来进行伴流的评估。WOF
的计算公式如下: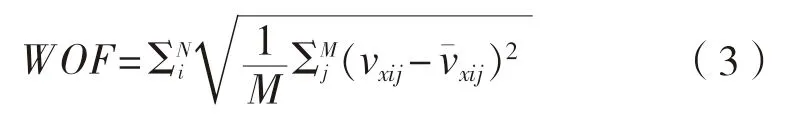
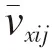
WOF
方法评价伴流,并选取具有代表性的0.7R
处作为伴流均匀度的评估标准,简化后的WOF
公式如下:
WOF
的数值越小,说明伴流场的均匀度越高。桨盘面上速度的监测点见图3。坐标原点位于桨盘中心,沿0.7R
半径处,每间隔10°
创建一个监测点,绕桨盘一周。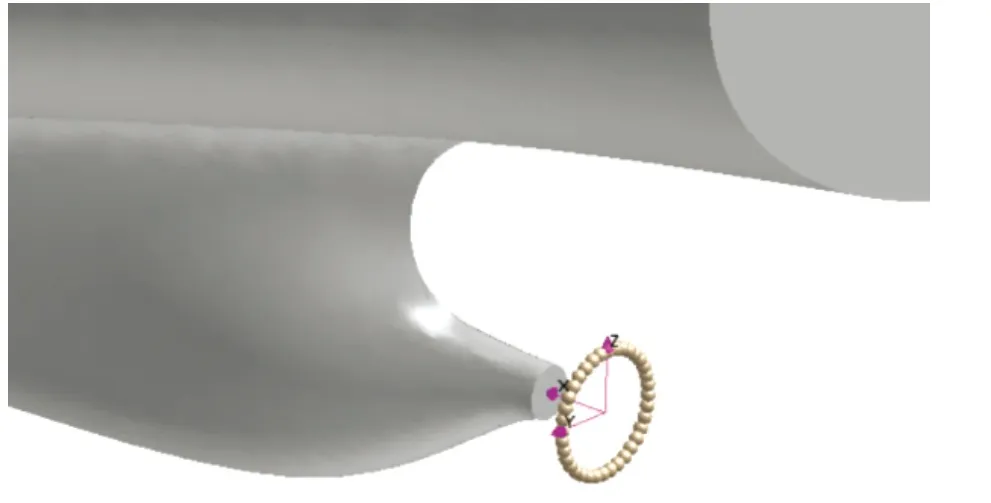
图3 桨盘上的监测点
2 双艉鳍船型的参数化建模
CAESES软件主要应用于产品设计前期的参数化建模及优化,具有三维参数化建模及变形控制、耦合仿真软件进行性能评估、自动化优化等功能。
本文中创建的双艉鳍集装箱船的主要参数如表2所示,按照船体线型的设计习惯三维建模采用实尺度,建模完成后再缩放到模型尺度用于CFD计算。

表2 船舶主要参数
CAESES软件具有2种参数化建模方式:
(1)半参数化建模方法
指在原有线型的基础上通过内置的变形方法进行参数化变形,变形操作简单,常用于母船型的局部修改。
(2)全参数化建模方法
将船体曲面通过参数及曲线控制的方式展开全新构建,进而实现参数化的控制。该方法建模更为复杂,且过程中的参数表达方式需要自行设计,但变形的灵活度更高,适用于新船型的设计优化。
由于船体左右对称,因此船壳的建模选用半船即可。以平行中体为分界,将船分为船尾、船舯和船首3个部分,其中船舯和船首两部分采用母船型的船壳,仅对船尾重新建模,并重点对双艉鳍的形状采用全参数化建模方法进行设计,以便得到变形方式灵活,变形探索空间更广的艉鳍。
根据双艉鳍的模型特点,将艉鳍分为内侧和外侧两部分,通过人为创建的分割平面对艉鳍进行分割,交界线落在分割平面上,即为艉鳍中心线。内侧和外侧两个曲面的构建思路相同,且共用1个特征剖线的定义编码(Feature)。具体的建模思路为:定义1根 NURBS 曲线,曲线上的控制点分别落在艉鳍边界线、中间形状控制线以及艉轴出口轮廓线这些特征线上;通过曲线生成器(Curve Engine)将特征线与Feature中的特征参数进行关联,最后由曲面生成器(Meta surface)按照由各特征线的起点(上端点)出发到其终点(下端点)结束的顺序对艉鳍的内外侧曲面分别进行构建。创建好的船尾模型,如图4所示。
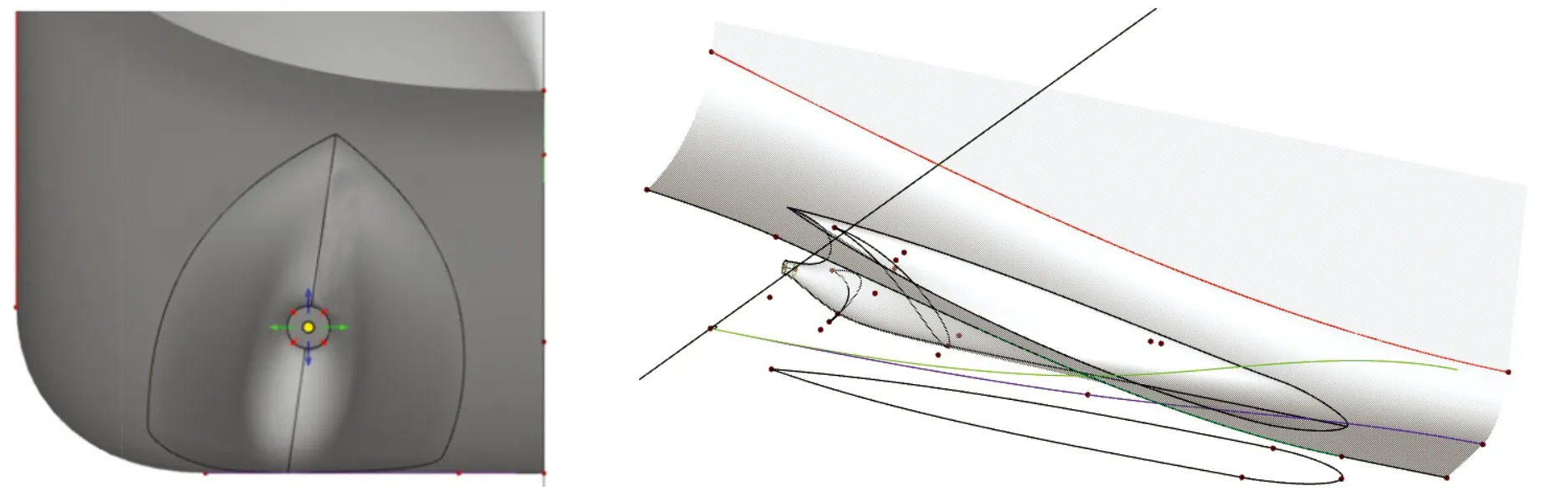
图4 双艉鳍参数化模型
双艉鳍的参数化设计主要有控制艉鳍间距、倾斜角度、艉轴出口位置以及艉鳍胖瘦的相关参数,可为后续的设计优化服务。
3 总阻力和艉流场优化
优化过程共分为2个阶段:第1阶段采用Sobol随机取样方法对最佳方案进行探索,样本数为20个;第2阶段以第1阶段的最佳设计方案作为基础方案,并采用NSGA-Ⅱ优化算法进行优化,遗传代数为3代,种群规模设置8个,交叉概率0.9,突变概率0.01。
3.1 设计变量
优化过程中所选取的设计变量见表3,表中的设计变量均在CAESES软件中针对实尺度模型创建。

表3 设计变量
3.2 约束条件
对设计吃水下的排水量进行约束,新的排水体积V
在原始数据的基础上浮动范围不超过0.4%,即:
3.3 优化目标
在船体线型优化过程中,若片面追求降低阻力,则可能导致桨盘面处的伴流品质变差。而伴流场不均匀不仅影响推进效率,还是造成空泡不稳定、艉部激振和噪声的主要原因。为了避免此种情况,本次优化设定2个目标,分别为模型船的静水阻力(半船)和伴流目标函数WOF
,并将这2个目标变量同时降低作为优化方向。3.4 优化结果
通过CAESES软件与外部CFD求解器STARCCM+搭建一体化的设计平台,并依次启动Sobol和NSGA-Ⅱ两种算法展开优化。最终得到的优化结果见图5。
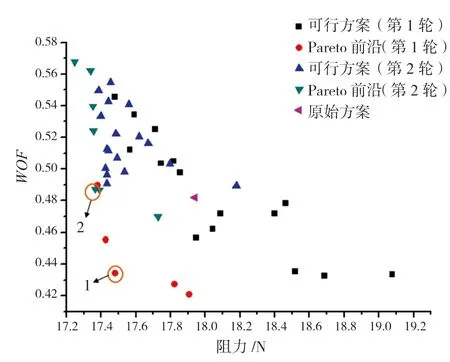
图5 可行方案及Pareto前沿
观察图5可知,经过第1轮计算得到第1轮优化后的Pareto前沿,从中选取最靠近坐标原点的优化方案1(已用圆圈标出),作为第2轮优化的基础设计方案;再经过第2轮优化得到新的Pareto前沿,并从中选取了优化方案2(已用圆圈标出)作为最优解。从所有的优化算例中可以看出,阻力值越小,伴流均匀度往往越差。在Pareto前沿上这一特征体现得更为明显,由此也可以看出这2个优化目标存在相互影响相互冲突的情况。对于多目标优化来说,设计人员可根据目标船型性能需求的不同,在Pareto前沿上选取最为合适的设计方案。
为了进一步比较本次优化的效果,将原始方案、优化方案1以及优化方案2这3个方案优化前后的设计变量及优化目标的变化进行对比,详细数据见表4,需要说明的是表中的排水体积为实尺度数值,阻力和WOF
则为读取的模型尺度仿真计算结果。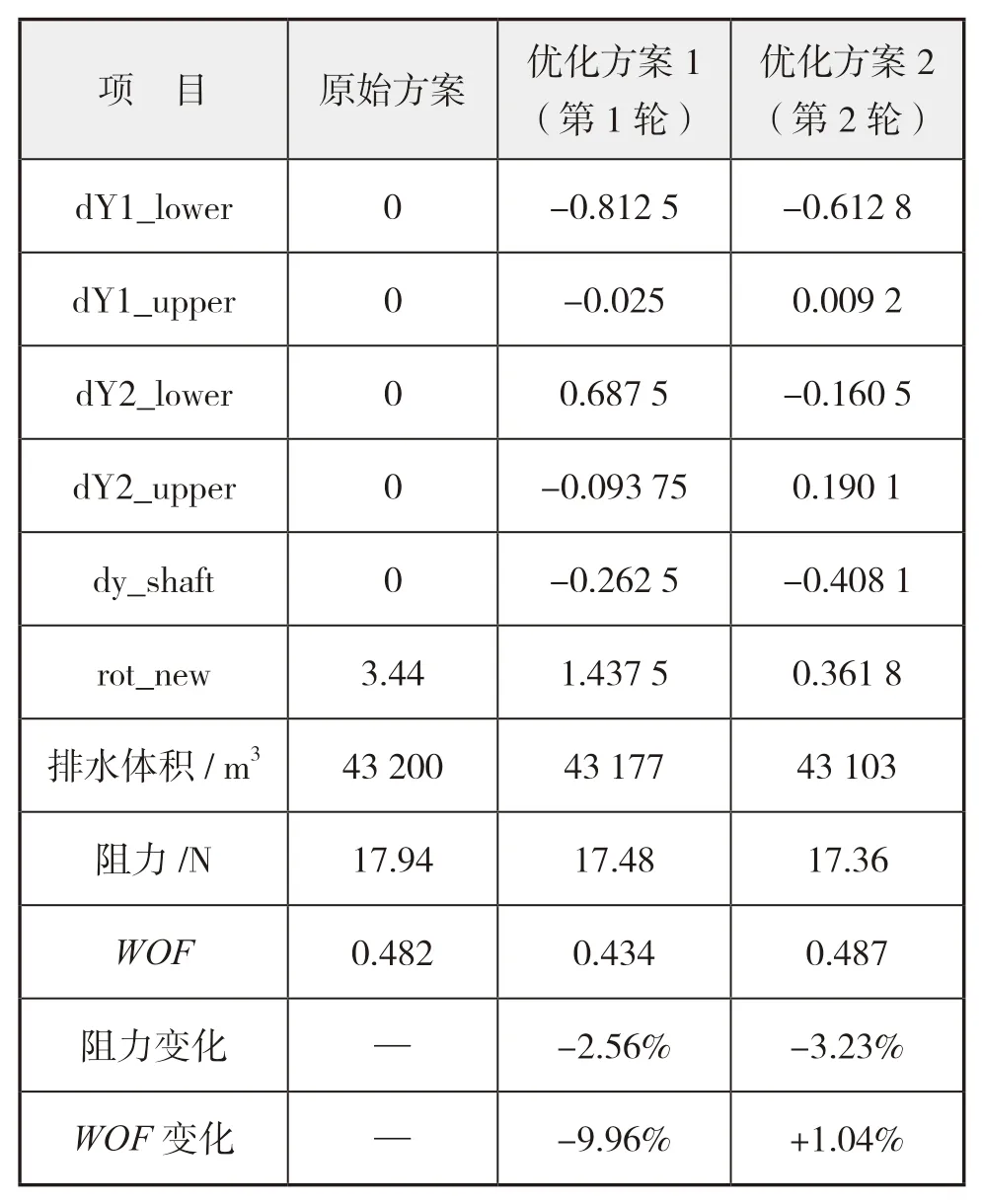
表4 优化前后的设计方案对比
经过优化后设计方案1的阻力和伴流目标函数WOF
分别降低2.56%和9.96%,优化方案2的阻力降低更为明显为3.23,但WOF
略有升高。此外,优化后的方案排水量均有小幅降低,也说明艉鳍的线型适当变瘦对阻力的性能提高有利。优化前后设计方案的线型对比如下页图6所示。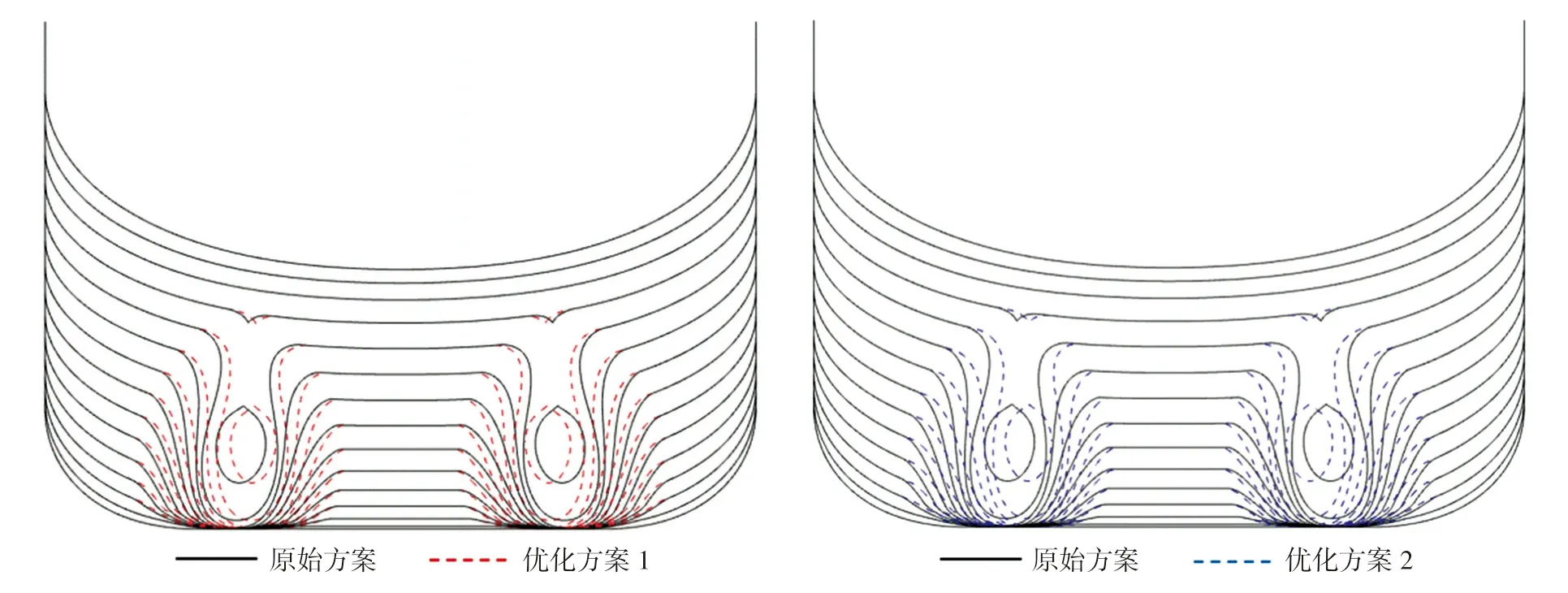
图6 优化前后的线型对比
由图6可以看出变化后的优化后的设计方案艉轴间距均减小了,且艉鳍的倾斜角度均变小了,艉鳍的形状变化后,桨盘处的伴流场也相应发生变化,伴流场的前后变化如图7所示。

图7 伴流场对比
由图7可见,优化前后桨轴中心上方的高伴流区变化更为明显。优化方案1的高伴流区范围有所降低,伴流场也更均匀,相比之下优化方案2的伴流均匀度则要差一些。
4 结 论
应用CAESES软件连接外部CFD求解器,搭建一体化的设计平台,并通过参数化设计,对1艘双艉集装箱船的双艉鳍进行优化,并得出以下结论:
(1) 采用全参数化方式构建双艉鳍船壳,不仅能够得到满足要求的原始线型,而且还能实现船型的自动变换,同时较好地确保新船壳的光顺性。
(2) 采用CFD仿真技术能够不但可以计算船体的航行阻力,还可以通过提取流场信息,分析伴流场的均匀度,较模型试验更为省时高效。
(3) 本研究共进行了2轮船型优化,综合来看,第1轮优化后的设计方案更优,阻力和伴流均匀度均有明显改善,有效避免单纯提高阻力性能而损失伴流均匀度的情况;第2轮优化在阻力性能上虽然获得更优化的设计方案,但综合性能并未进一步提高。
(4)在通常情况下,由于船舶的水动力优化计算量较大,在规定时间内所进行的优化探索也很有限;因此建议将提高优化策略的高效性或建立高精度的近似模型替代数值计算的方式作为后续的研究方向。
