基于高斯混合模型的列车随机振动加速度响应最大值分布统计分析
2021-09-06蒲珍华吴梦雪唐德发朱金李永乐
蒲珍华,吴梦雪,唐德发,朱金,李永乐
(1.西南石油大学 土木工程与测绘学院,成都 610500;2.西南交通大学 土木工程学院,成都 610031)

1.1 列车多体动力学模型


表1 列车模型主要参数表

图1 列车多体动力学模型
1.2 轨道不平顺数值模拟
基于中国高速铁路总体技术条件,建议对列车进行平稳性分析时使用德国高速线路轨道谱[14],且高速铁路试验段轨道谱的高低不平顺在30 m波长以上的平顺性基本与德国高速低干扰谱接近[15]。因此,选用德国高速低干扰谱,采用三角级数法对轨道不平顺序列进行模拟。在假设轨道不平顺为平稳遍历的高斯白噪声的前提下,轨道不平顺可看作是不同三角级数的叠加,可通过式(1)得到。
(1)
式中:f(x)为模拟得到的轨道不平顺序列;S(ωk)为功率谱密度函数,垂向不平顺单位为m2/rad/m,水平不平顺单位为1/rad/m;ωk为轨道不平顺的空间频率,rad/m;φk为第k个频率的相位,是独立均布于0~2π的随机数。
用三角级数法模拟得到的轨道不平顺功率谱密度(Power spectral density,PSD)与目标谱的吻合情况如图2所示,由图2可知,模拟的功率谱与目标谱吻合较好。

图2 轨道垂向不平顺模拟谱与目标谱的对比
1.3 列车加速度响应样本
以随机轨道不平顺作为输入激励,得到列车以200 km/h速度行驶时的加速度响应时程曲线,如图3所示。列车加速度测点位置根据《铁道车辆动力学性能评定和实验鉴定规范》(GB 5599—1985)规定设定于转向架中心上方横向1 m的车体地板上。
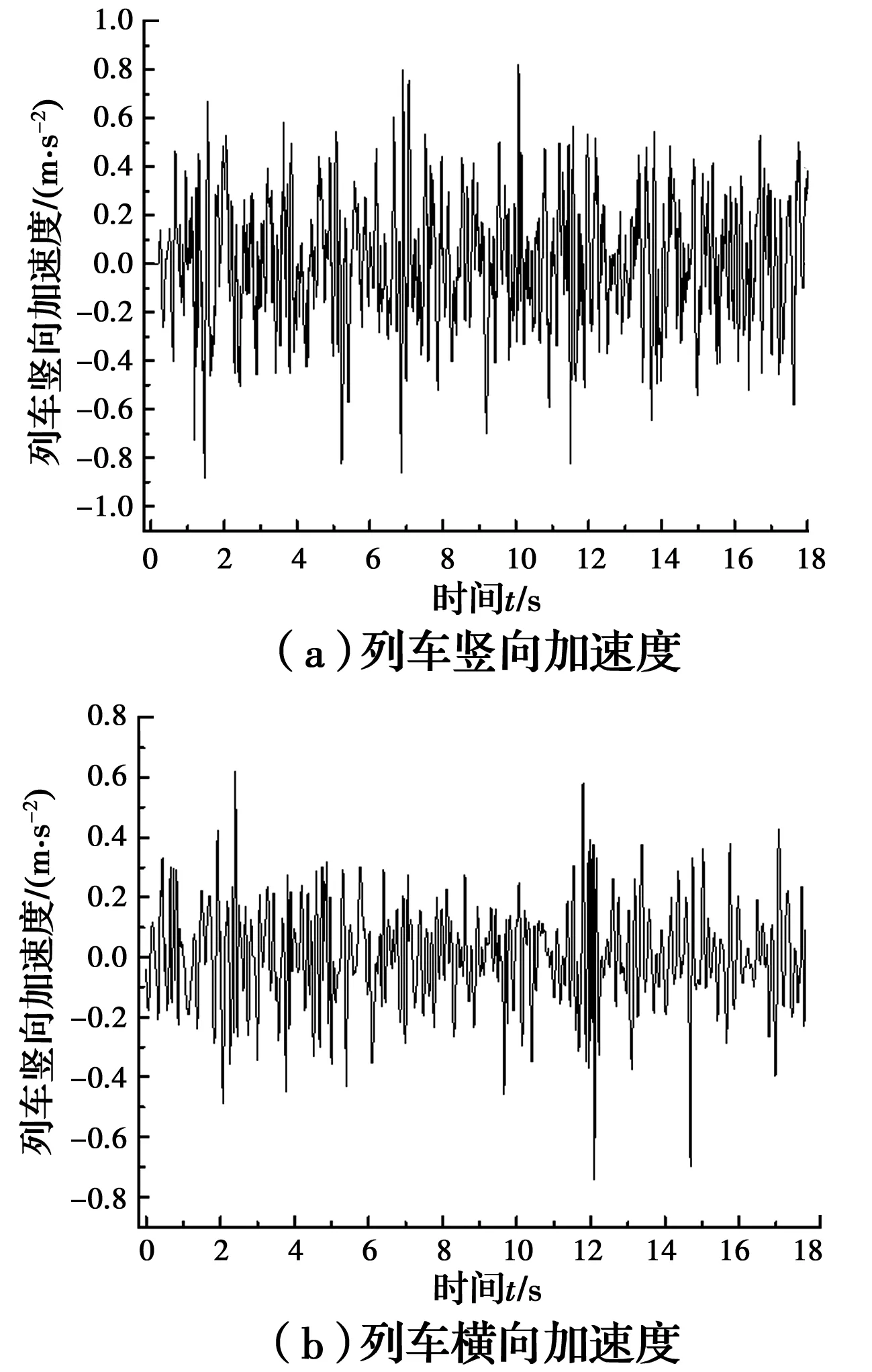
图3 轨道不平顺激励作用下的列车加速度响应
2 高斯混合模型
高斯混合模型广泛应用于统计分析领域[16],其作为一种统计模型,多用于构建概率密度函数,能较好地刻画参数空间中数据的分布及其特征,既具有非参数化方法的灵活性,又保持了参数化方法的精确性。高斯混合模型采用有限个特定概率分布密度函数的加权组合来拟合复杂的概率分布模型,通过选择混合分量的类型和个数,可逼近任何连续的概率分布密度函数。高斯混合模型(GMM)由高斯(正态)分布的加权组合得到,其概率密度函数为
(2)
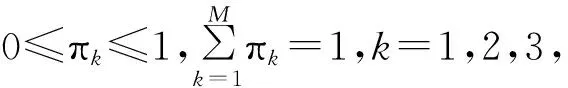
高斯混合模型可以逼近任何连续的概率分布函数,选择合适的权重系数是得出模型类型数量与模型参数的关键。高斯混合模型是一种“软分类聚类”,是基于假设数据集是由一个潜在的混合概率分布产生的,其中每个高斯分量都表示一个不同的聚类。首先通过估计样本数据集的混合概率密度,然后计算样本源中单个样本之于各个高斯分量的后验概率,最后将单个样本分配到后验概率最大的高斯分量所在的聚类组,从而得到样本数据集所服从的高斯混合分布[18]。
2.1 参数估计
高斯混合模型(GMM)的期望为
(3)
式中:πk为随机变量x取至第k个高斯成分的权重系数;N(xi;μk;∑k)为第k个类别的条件概率密度;μk、∑k分别为该高斯分量的均值和协方差矩阵。
对于高斯混合模型的参数,可用期望最大化(EM)算法进行迭代估计[19]。估计步骤为
1)E步
(4)
2)M步
(5)
(6)
(7)

3)收敛条件
不断迭代E步与M步,至似然函数的变化量小于误差值esp或迭代次数k≤K时,迭代结束,否则返回E步。随着迭代次数的增加,迭代误差越来越小,似然函数不断收敛。可接受的迭代误差esp=2×10-16,最大迭代次数K=500。似然函数为
(8)
综上所述,EM是一种迭代算法,也是一种聚类算法,它可以通过迭代求出高斯混合模型的参数,并将样本源中的单个样本通过迭代收敛性进行聚类。高斯混合模型聚类通常采用贝叶斯信息准则(BIC)选择模型,模型的BIC值越大,该模型就越符合实际。
2.2 拟合度检验
假设列车振动加速度响应的最大值服从高斯混合分布,采用期望最大化算法对该概率模型参数进行最大似然估计,再进行拟合度检验。
为了对比得到的高斯混合模型概率密度函数与由列车加速度响应最大值的样本序列得到的频率直方图的拟合效果,采用拟合优度(AdjustedR2)与均方根误差(Root Mean Squared Error,RMSE)两项指标来对概率密度分布曲线的拟合优劣程度进行评价。拟合优度用于评价概率密度分布曲线与直方图之间的相似程度,该值越接近于1,表示拟合程度越好;均方根误差用于评价概率密度分布曲线与直方图之间的偏离程度,该值越接近于0,表示偏离程度越小,拟合程度越好。
2.3 样本量
样本量是指从总体中抽取的样本元素的总个数,样本量的大小是选择检验统计量的一个重要要素。由抽样分布理论可知,在大样本条件下,如果总体为正态分布,则样本统计量服从正态分布;如果总体为非正态分布,则样本统计量渐近地服从正态分布[20]。
样本量的计算公式为
(9)
式中:n为样本量;α为显著水平;Zα/2为置信区间对应的标准分数;E为估计误差,一般小于0.1;σ为标准差,一般为0.5。
在确定样本量时,取α为0.05,则置信度为95%,经查表,Zα/2为1.96;假定的估计误差为0.05,则最小样本量为n=384。在满足样本最小容量的情况下,增加样本量有助于增加检验统计的精度,提高可靠性。
3 列车加速度响应最大值的概率模型
基于Monte-Carlo方法,分别取400、500、600、700、800、900和1 000个随机生成的轨道不平顺样本,计算得到列车的加速度响应时程样本,并将列车竖向和横向加速度响应的最大值作为随机变量,采用EM算法进行聚类分析,比较聚类为1~4类的BIC值,并选择BIC值最大的一组参数,得出某个确定样本容量下列车加速度响应最大值所服从的高斯混合模型。接着,对比不同样本容量下列车加速度响应最大值的高斯混合模型与其相应频率分布直方图的拟合优度及均方根误差,从中选取合适的高斯混合模型概率密度函数(对应的样本容量记为Nrep)作为代表该车速下列车加速度响应最大值的概率密度模型,此时的样本容量Nrep作为代表该车速下列车加速度响应最大值概率统计特征的最优样本数量。
3.1 列车竖向加速度
当列车以200 km/h车速行驶时,以1 000个列车竖向加速度响应样本为例,表2为列车竖向加速度最大值不同聚类个数的BIC值。由表2可得,当聚类个数N=2时,BIC值最大。表3为N=2时模型的参数估计值。将表3中的参数带入到式(2)中,即可得到列车竖向加速度最大值所服从的高斯混合模型概率密度函数,如式(10)所示。图4为得到的高斯混合模型概率密度函数与相应样本数量下列车竖向加速度响应最大值的频率分布直方图的对比,从图4可知,其拟合效果较好。
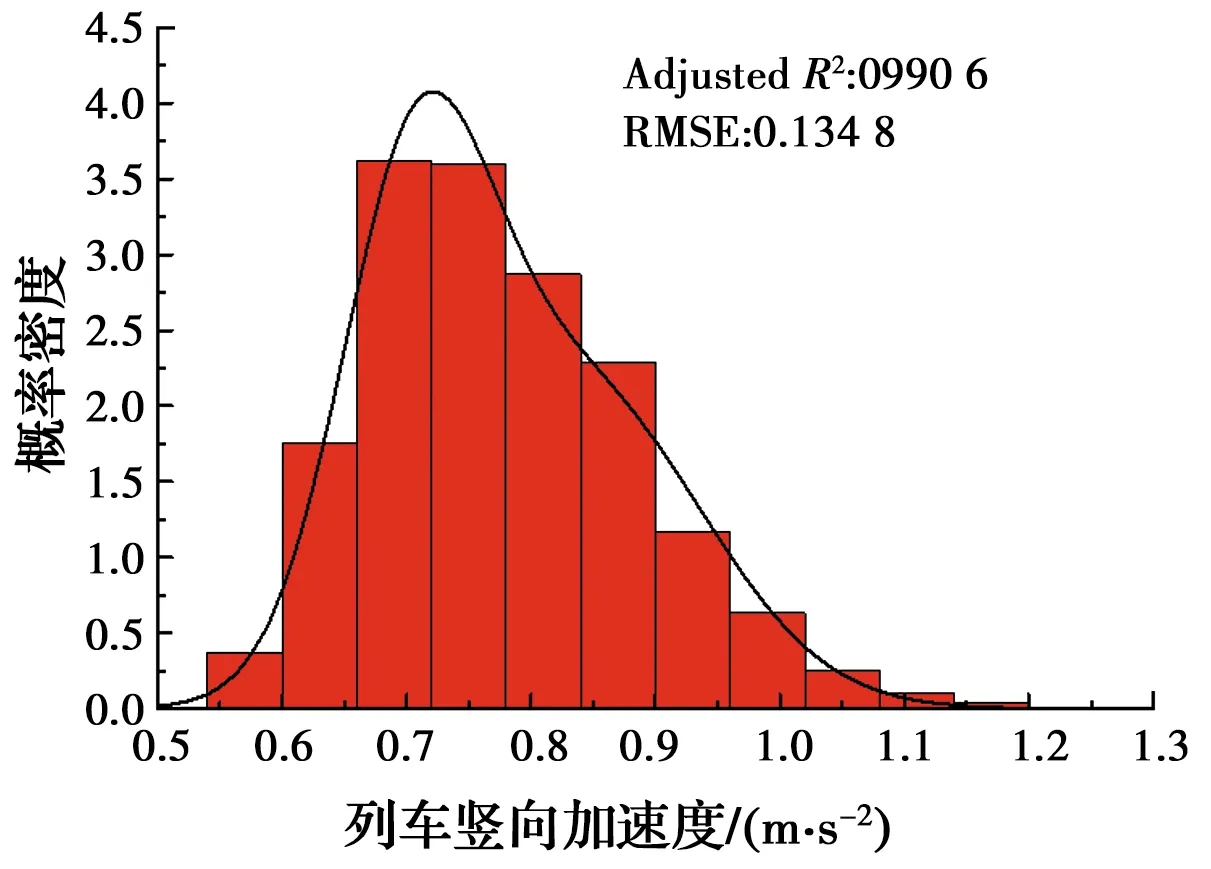
图4 列车竖向加速度最大值的概率密度分布
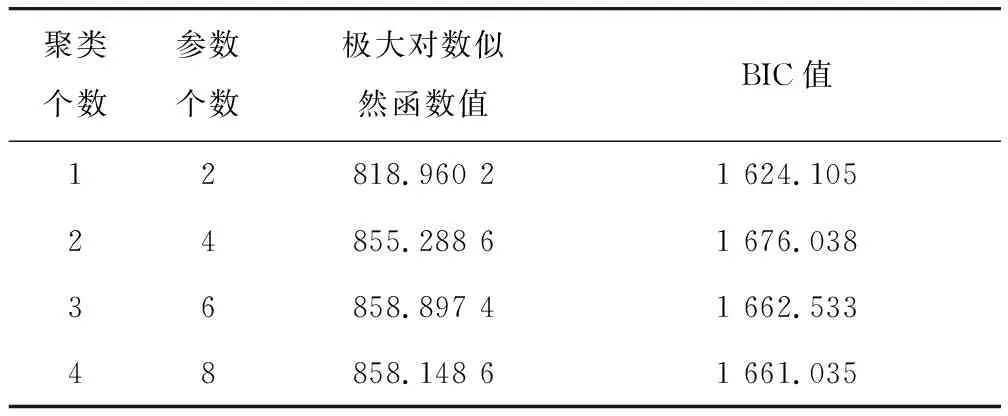
表2 列车竖向加速度最大值不同聚类数的BIC值
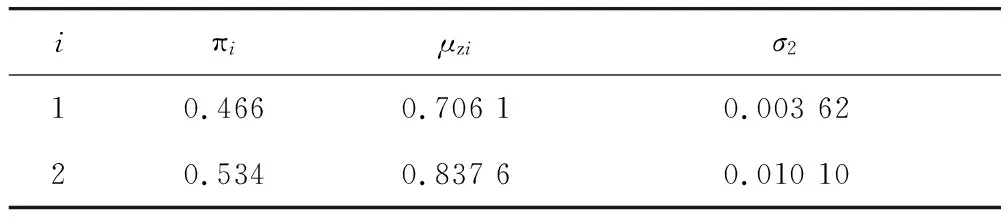
表3 N=2时模型参数估计值
(10)
分别取400、500、600、700、800、900和1 000个随机生成的轨道不平顺样本,计算得到车速为200 km/h时不同样本容量下的列车竖向加速度响应最大值的高斯混合模型概率密度分布与其频率分布直方图的拟合优度及均方根误差,如表4和图5所示。由表4和图5可知,当样本数量为400~700时,列车竖向加速度响应最大值的高斯混合模型概率密度分布与其频率分布直方图的拟合优度随着样本数量的增加逐渐变大,在样本数量达到700后趋于稳定;而均方根误差随着样本数量的增加逐渐减小,在样本数量达到700后,波动较小,趋于稳定。因而,车速为200 km/h时,代表列车竖向加速度响应最大值概率统计特征的最优样本数量Nrep=700。图6为不同样本数量下的列车竖向加速度最大值所服从的高斯混合模型的概率密度曲线。

表4 列车竖向加速度最大值概率分布的拟合指标
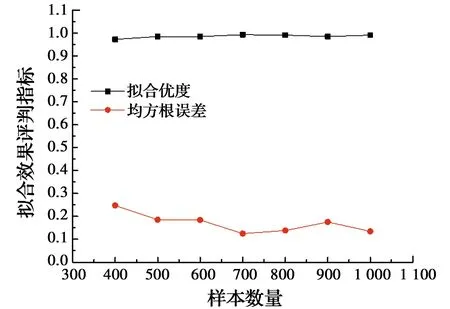
图5 不同样本数量下列车竖向加速度最大值概率密度曲线拟合效果评判指标对比
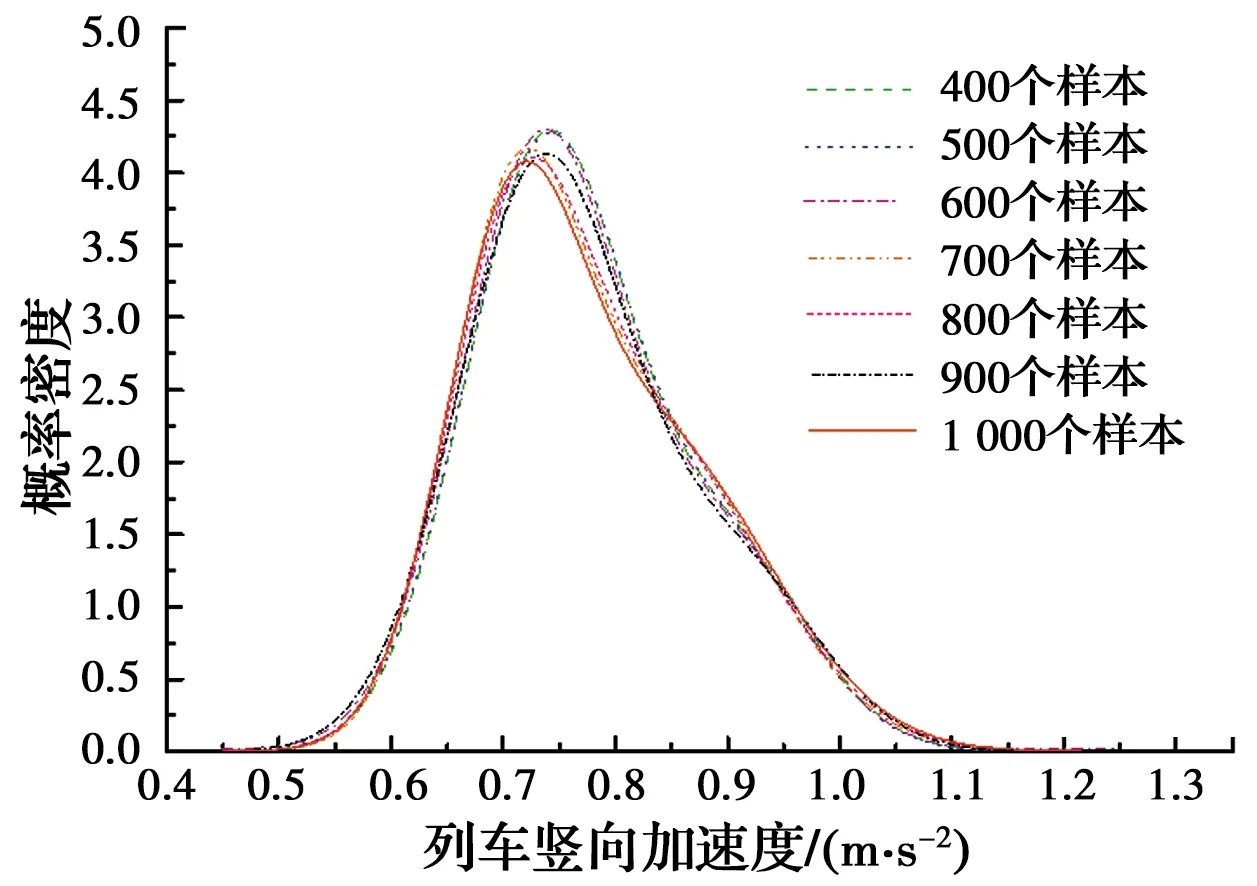
图6 不同样本数量的列车竖向加速度最大值概率密度曲线
当车速分别为100、150、200 km/h时,不同样本数量下列车竖向加速度响应最大值的高斯混合模型概率密度分布与其频率分布直方图的拟合优度及均方根误差如图7所示。从图7中可以看出,在样本数量达到700后,3种不同车速下的列车竖向加速度响应最大值的高斯混合模型概率密度分布与其频率分布直方图的拟合优度和均方根误差均波动较小,趋于稳定。因而当车速分别为100、150、200 km/h时,代表列车竖向加速度响应最大值概率统计特征的最优样本数量Nrep均可取为700。

图7 不同车速和样本数量下列车竖向加速度最大值概率密度曲线拟合效果评判指标对比
3.2 列车横向加速度
当列车以200 km/h车速行驶时,仍以1 000个列车横向加速度响应样本为例,表5为列车横向加速度最大值不同聚类个数的BIC值,由表5可得,当聚类个数N=3时,BIC值最大。表6为N=3时模型的参数估计值。将表6中的参数带入式(2)中即可得到列车横向加速度最大值所服从的高斯混合模型的概率密度函数,如式(11)所示。图8为得到的高斯混合模型的概率密度函数与相应样本数量下列车横向加速度响应最大值的频率分布直方图的对比,由图8可知其拟合效果较好。

图8 列车横向加速度最大值的概率密度分布

表5 列车横向加速度最大值不同聚类数的BIC值

表6 N=3时模型参数估计值
(11)
分别取400、500、600、700、800、900和1 000个随机生成的轨道不平顺样本,计算得到车速为200 km/h时不同样本容量下列车横向加速度响应最大值的高斯混合模型概率密度分布与其频率分布直方图的拟合优度及均方根误差,如表7和图9所示。由表7和图9可知,列车横向加速度响应最大值的高斯混合模型概率密度分布与其频率分布直方图的拟合优度和均方根误差在样本数量达到800后波动较小,趋于稳定。因而,车速为200 km/h时,代表列车横向加速度响应最大值概率统计特征的最优样本数量Nrep=800。图10为不同样本数量下列车横向加速度最大值所服从的高斯混合模型的概率密度曲线。
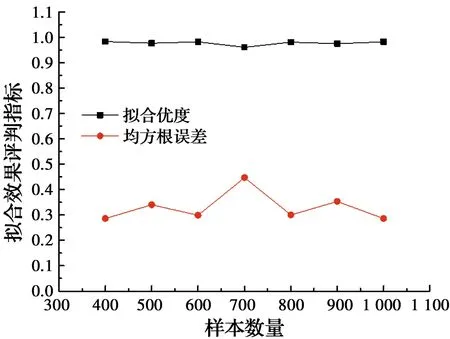
图9 不同样本数量下列车横向加速度最大值概率密度曲线拟合效果评判指标对比
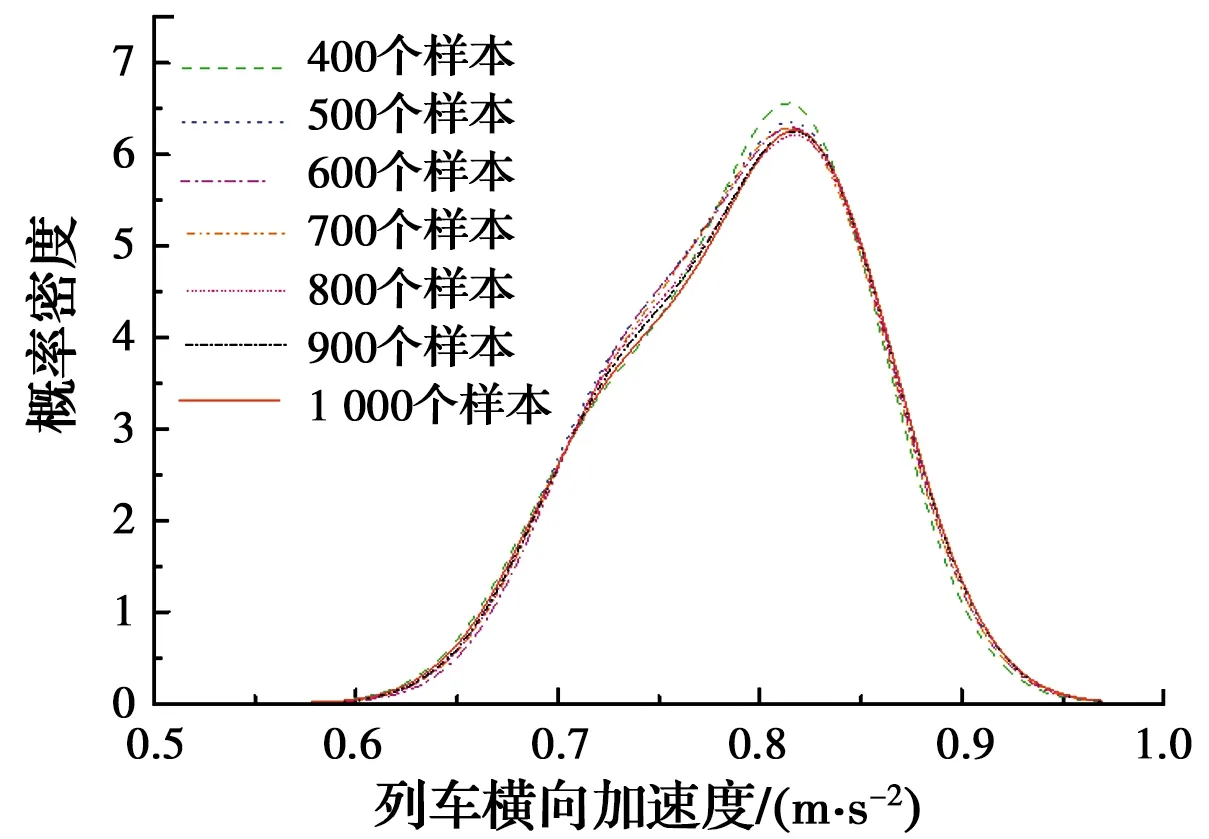
图10 不同样本数量的列车横向加速度最大值概率密度曲线

表7 列车横向加速度最大值概率分布的拟合指标
当车速分别为100、150、200 km/h时,不同样本数量下列车横向加速度响应最大值的高斯混合模型概率密度分布与其频率分布直方图的拟合优度及均方根误差如图11所示。从图11中可以看出,在样本数量达到800后,3种不同车速下列车横向加速度响应最大值的高斯混合模型概率密度分布与其频率分布直方图的拟合优度和均方根误差均波动较小,趋于稳定。因而当车速分别为100、150、200 km/h时,代表列车横向加速度响应最大值概率统计特征的最优样本数量Nrep均可取为800。
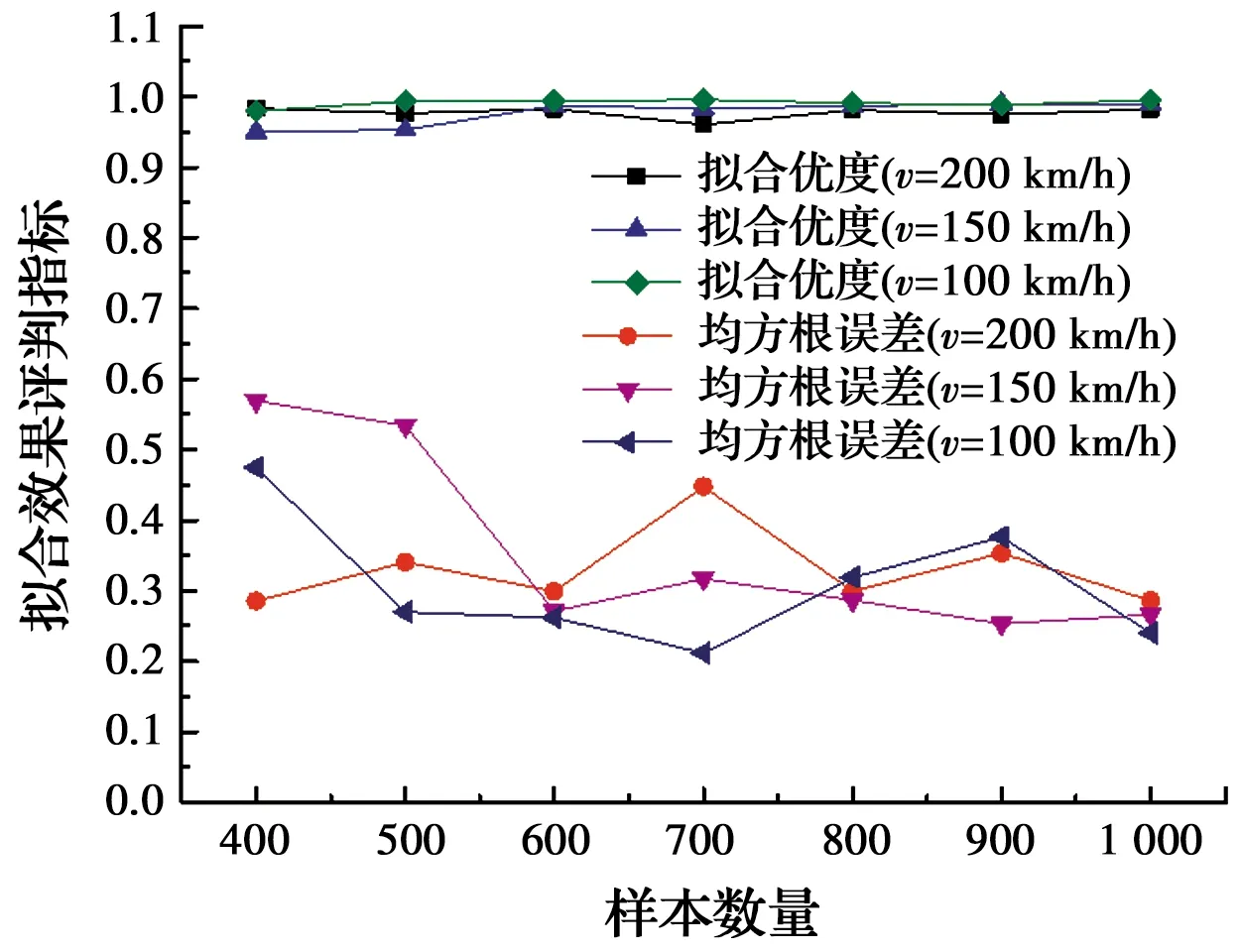
图11 不同车速和样本数量下列车横向加速度最大值概率密度曲线拟合效果评判指标对比
4 不同车速下列车加速度响应最大值的统计规律
列车分别以车速100、150、200 km/h行驶1 000 m,基于Monte-Carlo方法,取1 000个随机生成的轨道不平顺样本计算得到列车的加速度响应时程样本。通过统计列车的竖向加速度最大值及横向加速度最大值,得到列车不同车速下的加速度最大值箱型图,如图12所示。由图12可知,列车的竖向加速度最大值和横向加速度最大值均随着车速的增加逐渐变得离散;列车的竖向加速度最大值和横向加速度最大值的均值随着车速的增加而增加。此外,列车竖向加速度最大值的均值都大于中位数,而列车横向加速度最大值的均值在车速为100、150 km/h时大于中位数,在车速为200 km/h时的均值小于中位数。

图12 不同车速下的列车加速度最大值箱型图
通过对列车的竖向加速度最大值样本及横向加速度最大值样本进行分析,进一步得到不同车速下列车加速度最大值的概率密度分布图,如图13所示。从图13中可知,列车竖向加速度最大值和横向加速度最大值的概率密度曲线均沿着横坐标向右移动。另外,与车速为100、150 km/h相比,车速为200 km/h时列车竖向加速度与横向加速度最大值的概率密度曲线的分布范围均更大;而车速为100 km/h时列车竖向加速度与横向加速度最大值的概率密度曲线最为高耸。这表明随着车速的增加,列车加速度响应最大值分布的离散性增强。
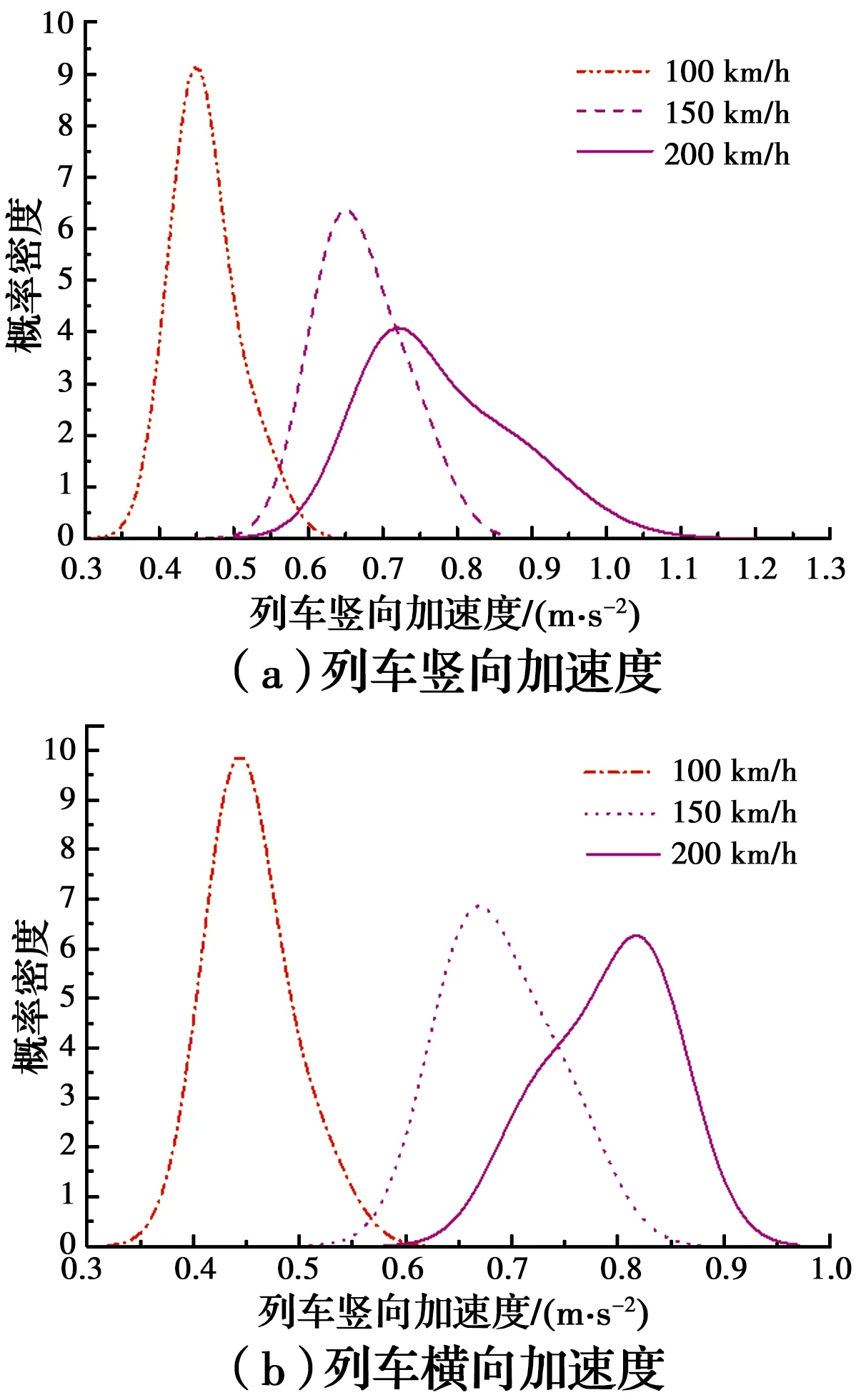
图13 不同运行车速下列车加速度最大值的概率密度曲线
由于列车振动会使乘车人员产生不适感或疲劳,因而引入平稳性指标来度量乘客乘车时的舒适程度。参考高速铁路客车动力学性能评定资料,中国车体振动加速度的平稳性标准界限值可取为:竖向振动加速度av≤1.3 m/s2,横向振动加速度ah≤1.0 m/s2。
在运行距离为1 000 m的情况下,选择列车运行车速为100、150、200 km/h的工况,得到列车加速度最大值随机变量的累积分布函数(Cumulative distribution function, CDF)曲线,如图14~图16所示。从图中可以发现,列车在运行车速为100、150、200 km/h时的竖向加速度与横向加速度均满足平稳性要求。
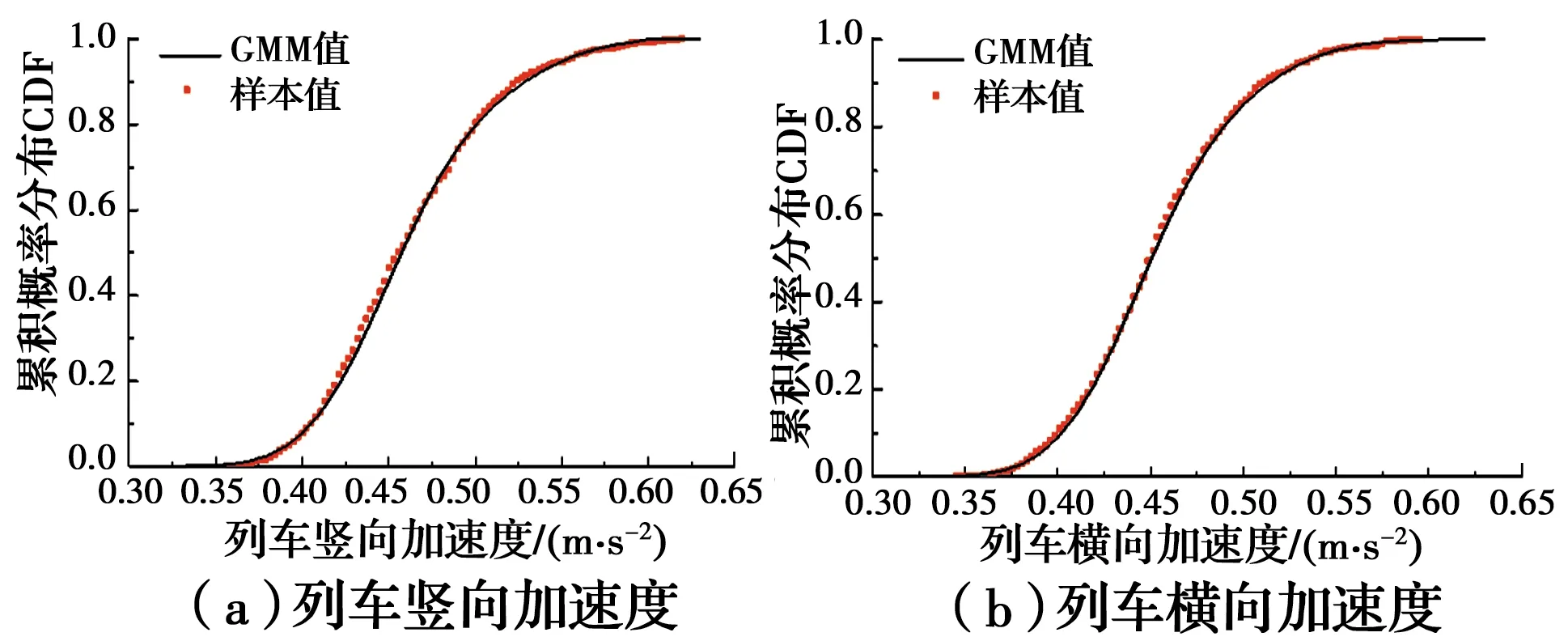
图14 100 km/h的列车加速度最大值的累计分布函数曲线

图15 150 km/h的列车加速度最大值的累计分布函数曲线

图16 200 km/h的列车加速度最大值的累计分布函数曲线
5 结论
1)采用高斯混合模型能够有效地拟合列车加速度响应最大值的分布规律。
2)当车速分别为100、150、200 km/h时,列车竖向加速度响应的样本数量达到700时可较好地代表列车竖向加速度响应最大值的概率统计特征;而列车横向加速度响应的样本数量达到800时能较好地代表列车横向加速度响应最大值的概率统计特征。
3)列车的竖向加速度最大值和横向加速度最大值均在车速为100 km/h时分布最为集中;整体来讲,随着车速的增加,列车加速度响应最大值分布的离散性增强。
