大悬挑空间网架屋盖—树状编织筒壳支承结构的稳定性研究

周鼎 吴岸

1.武汉市政工程设计研究院有限责任公司 430070

2.武汉理工大学 430070

引言

近年来，空间网架结构凭借其轻质高强、生产安装便利、外观优美等特点，广泛应用于大跨建筑结构的屋盖中［1－3］。作为大跨空间网架的支承结构，树状仿生结构的应用，极大地增加了大跨空间结构建筑面积的利用率，使支承节点域内的应力分布更加均匀［4－6］。

然而大跨度空间网架及其树状支承结构的缺点是节点杆件受力复杂，结构整体稳定性差，极易发生整体倾覆，因此针对该类建筑结构的稳定性分析显得十分重要。目前，国内外学者针对空间网架结构的稳定性进行了大量的研究，并取得了较多的成果。Dhatt和Batoz等［7］在非线性结构稳定问题的牛顿法基础上提出了位移增量法。He等［8］对圆柱形网架结构的稳定性进行研究，分析了结构可能出现的屈曲模态以及不同条件下的极限承载力。杨伦［9］对某机场T3 航站楼网架屋盖进行了特征值屈曲分析、几何线性屈曲分析和弹塑性全过程稳定性验算，结果表明该网架屋盖具有一定的延性，稳定性满足要求。刘记雄等［10］利用SPA2000 对开洞和不开洞网架结构分别进行了线性和非线性屈曲分析，研究了开洞大小及位置对网架结构稳定性的影响。袁棪等［11］以某大学体育馆平板网架结构为研究对象，从整体稳定性、温差作用两个方面对整体结构（带支撑）和上部结构单独计算的整体工作性能进行对比分析。结果表明，单独计算的上部网架结构所得的稳定性承载力较大，偏于不安全。

本文在上述研究基础上以某大悬挑空间网架屋盖—树状编织筒壳支承结构为研究对象，对其稳定性进行研究。采用MIDAS 及ABAQUS 对结构进行线性、几何非线性和几何材料双重非线性屈曲分析，观察其屈曲模态及失稳破坏形式。并根据屈曲模态结果确定失效构件，完成关键构件失效后的稳定性计算。

1 工程概况

1.1 工程背景

广东省某大悬挑空间网架屋盖及其树状编织筒壳支承结构，其屋盖采用局部双层具有明显曲率的大悬挑空间网架结构。网架为四角锥网架结构，网架支承最大跨度60m，最大悬挑23.5m，高度20m。网架结构中部的树形编织体支承是由12 个V 型圆钢管竖向通过多级分支三维展开，呈树状结构相贯交织在一起，形成空间筒壳结构如图1 所示。其节点形式呈X型、Y型和根部作用的V型。材料属性见表1。

图1 大悬挑空间网架屋盖—树状编织筒壳支承结构Fig.1 Large cantilevered grid roof with treelike braided cylindrical shell

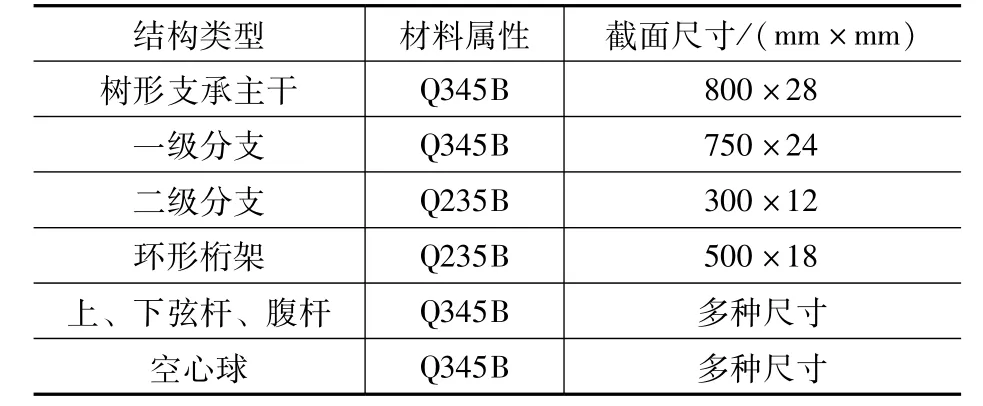
表1 结构材料Tab.1 Structural materials

1.2 荷载组合

结构抗震设防烈度为7 度，设计基本地震加速度为0.10g，地面粗糙度类别为B 类。根据实际情况确定结构计算的荷载取值。（1）网架屋面恒荷载标准值：上弦层0.75kN／m2、下弦层0.30kN／m2；（2）网架屋面活荷载标准值：上弦层0.50kN／m2、下弦层0.50kN／m2；（3）基本风压：0.65kN／m2（100 年重现期）、0.6kN／m2（50年重现期）；（4）基本雪压：无。

大悬挑空间网架屋盖—树状编织筒壳支承结构根据《建筑结构荷载规范》（GB 50009—2012）［12］进行荷载组合，得到的静力荷载工况组合如表2 所示。

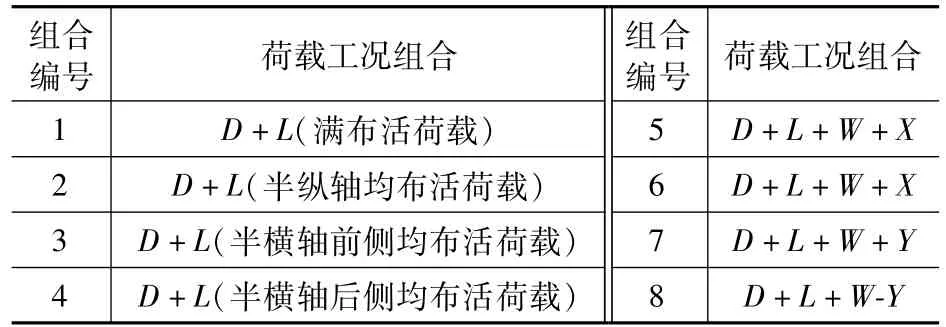
表2 荷载组合Tab.2 Load combination

2 线性屈曲分析

线性屈曲分析是对理想结构的整体稳定分析，不包含几何缺陷和材料的非线性，其得到的屈曲临界荷载反映的是结构极限荷载的上限值。通常在进行整体结构的非线性分析之前，需要引入线性屈曲模态作为初始缺陷的分布形式，因此非常有必要进行线性屈曲分析。

2.1 最不利荷载组合

用midas Gen软件按照表2 中的8 种工况组合对结构进行线性屈曲分析，以获得不同荷载工况下的屈曲荷载系数。表3 给出了8 种工况下结构的前5 阶线性屈曲荷载系数。

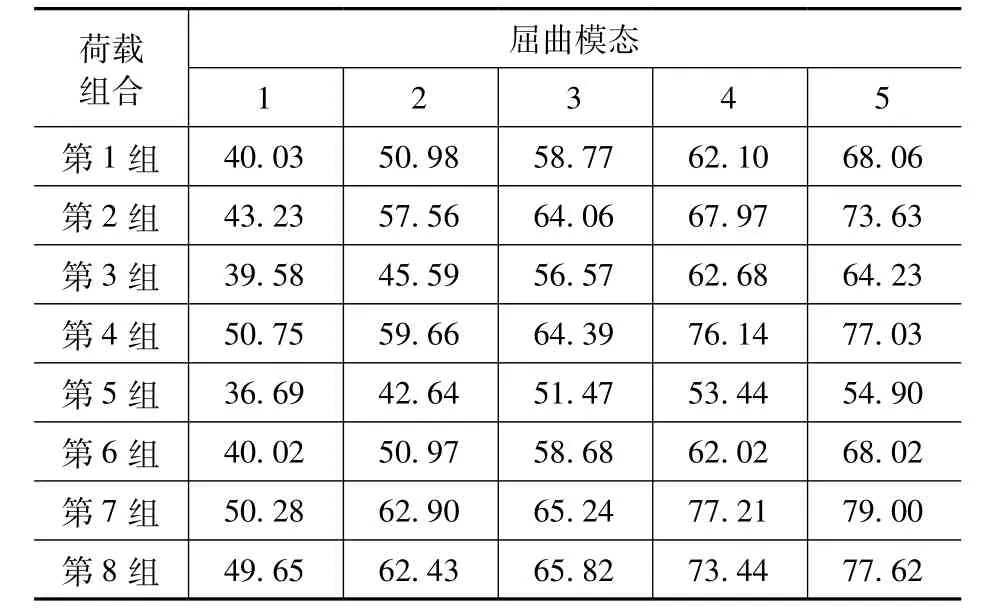
表3 8 种工况下的前5 阶线性屈曲荷载系数Tab.3 Linear buckling load coefficients of the first five orders under 8 working conditions

屈曲临界荷载等于屈曲临界系数与所施加荷载的乘积，即屈曲临界系数越小，其整体稳定性越低。由表3 结构前5 阶屈曲临界荷载系数的趋势可知，第5 组荷载组合是最不利工况组合。

2.2 失稳模态

图2 为ABAQUS 计算的荷载组合5（D＋L＋W＋X）作用下结构前5 阶线性屈曲失稳模态。从图中可知，前5 阶屈曲失稳主要发生在屋盖网架结构以及树状支承的前侧，其中以树状支承结构节点处更为明显。主要是由于结构在第5 种荷载组合下，横向风荷载比较强烈，而结构的横向刚度较弱，导致该部位率先发生失稳。

图2 屈曲模态Fig.2 Buckling mode diagram

通过对比ABAQUS 与MIDAS 计算的前5 阶线性屈曲荷载系数（表4），发现屈曲荷载系数的变化规律基本一致，皆随模态阶数的增加而增加。前5 阶模态屈曲荷载系数的最大误差在8%以内，平均误差为5.71%，验证了所采用的模型及计算方法的正确性，计算模型及结果可用于后续的非线性屈曲分析。

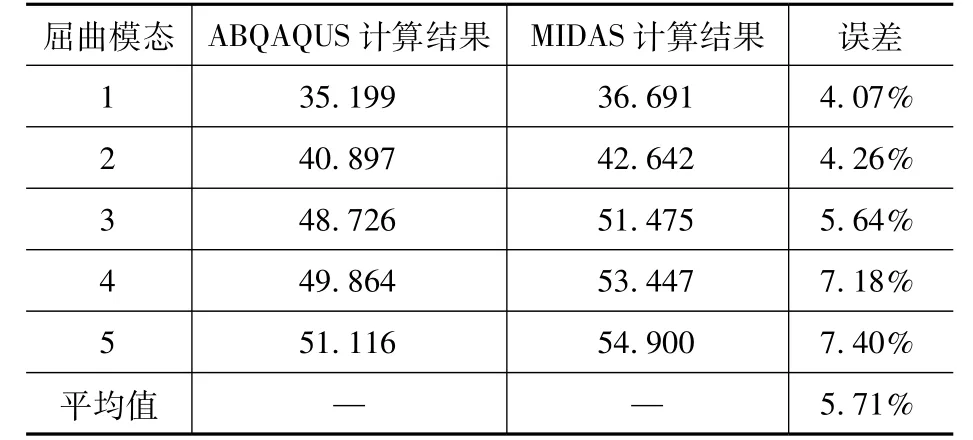
表4 前5 阶屈曲模态对比Tab.4 Comparison of the first five buckling modes

3 非线性屈曲分析

3.1 几何非线性屈曲分析

目前在进行结构几何非线性屈曲分析时，一般采用一致模态缺陷法，即用最低阶的屈曲模态来模拟初始几何缺陷对结构的影响。研究表明初始缺陷达到空间最大跨度的1／300 时，缺陷对结构承载力才会产生较大影响。初始缺陷取L／300、L／200、L／100 即200mm、300mm、600mm（L为最大跨度60m）。

表5 为在第5 组最不利荷载组合工况下利用ABAQUS和MIDAS 计算的不同初始缺陷的几何非线性屈曲系数。从表中发现，屈曲系数随着初始缺陷取值的增大而减小；初始缺陷对结构几何非线性稳定承载力影响较小，承载力下降5%～10%。MIDAS和ABAQUS的计算结构误差在6%以内，说明两种软件计算的几何非线性结果较为合理，同时也说明该结构为缺陷不敏感结构。

表5 几何非线性屈曲荷载系数Tab.5 Geometric nonlinear buckling load coefficient

图3 为利用ABAQUS计算荷载组合5 工况下的几何非线性屈曲临界荷载系数与竖向最大位移之间的关系曲线。从图中可以发现，荷载组合5工况下带缺陷结构的几何非线性屈曲分析（L／300）得到的稳定性承载力为基本荷载的23.66倍，表明结构具有较好的稳定性；屈曲系数在达到临界点之前，竖向位移随着荷载的增大而增大。

图3 几何非线性屈曲临界荷载系数-竖向最大位移曲线Fig.3 The curve of geometric nonlinear buckling load coefficient and vertical maximum displacement

3.2 双重非线性屈曲分析

对于网架结构这类厚度相对于跨度很小的柔性结构，几何非线性分析虽然能反映其整体的稳定性，但不能排除网架结构部分杆件在结构达到临界荷载之前就进入弹塑性状态。因此，对于重要结构，既考虑几何非线性又考虑材料非线性的双重非线性分析最能反映结构的真实情况。

表6 为采用ABAQUS对结构进行双重非线性屈曲分析的屈曲荷载系数，荷载选择第5 组最不利荷载组合工况，初始缺陷值分别取L／300、L／200、L／100，钢材采用双折线模型。从表中可以发现，结构的双重非线性屈曲荷载系数明显小于几何非线性荷载系数，造成二者计算结果相差较大的原因主要是由于结构发生屈曲时产生了较大的变形，在考虑材料非线性后，屈曲部位杆件应力超过了材料屈服应力进入塑性阶段。

表6 双重非线性屈曲荷载系数Tab.6 Double nonlinear buckling load coefficients

从图4 不同缺陷下双重非线性屈曲荷载系数随竖向位移的变化曲线可知，屈曲系数随着初始缺陷的增大逐渐减小，在结构达到临界荷载之前均随着竖向位移的增加而增加。初始缺陷的变化使非线性承载力降低8%～16%，说明结构为缺陷不敏感结构。

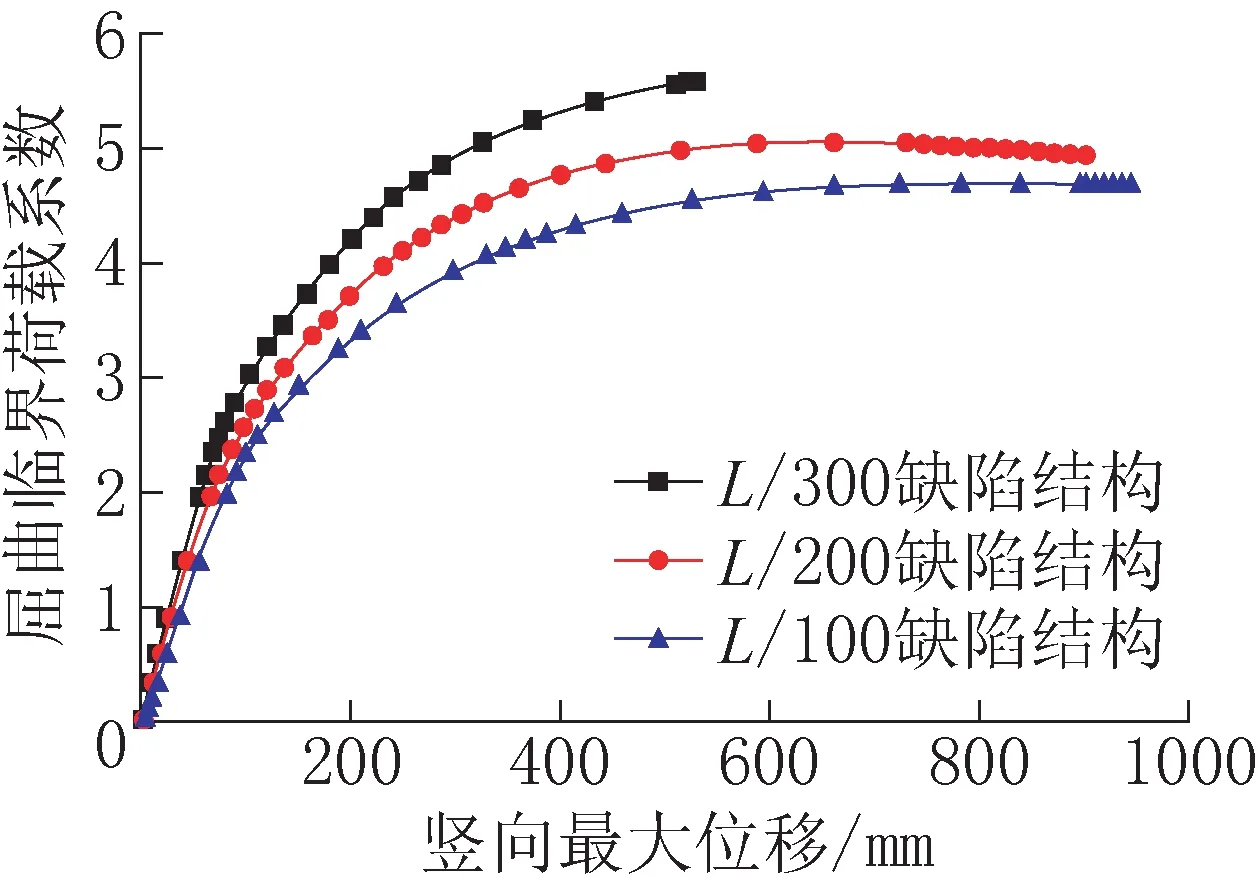
图4 双重非线性屈曲临界荷载系数-竖向最大位移曲线Fig.4 The curve of double nonlinear buckling load coefficient and vertical maximum displacement

3.3 关键构件失效的双重非线性屈曲分析

由前文结构的屈曲模态分析可知，结构在第5 种最不利荷载组合工况下屈曲失稳主要发生在屋盖网架结构以及树状支承的前侧，其中以树状支承结构节点处更为明显。因此，在对屈曲模态失稳形式研究的基础上，总结出以下4 种关键构件的失效可能会对结构整体稳定性产生较大的影响：失效构件1 为树状编织筒壳结构前侧Y型节点的主干构件；失效构件2 为其相邻的Y型节点的分支构件；失效构件3为X型节点的分支构件；失效构件4 为屋盖桁架下部支承构件。如图5 所示。在进行失效杆件的双重非线性屈曲分析时，对失效的关键构件用非常小的刚度进行模拟，初始缺陷取L／300，钢材采用双折线模型。

图5 关键构件失效布置Fig.5 Failure diagram of key components

图6 绘制了在第5 组荷载组合工况下，不同关键部位构件失效后的双重非线性屈曲荷载系数与竖向最大位移的关系曲线，并将得到的屈曲荷载系数列于表7。从图6 和表7 中可以发现，不同部位关键构件的失效均会影响结构受力性能，会使结构稳定性下降。树状编织筒壳结构前侧Y型节点的主干构件失效会导致屈曲临界荷载降低约15.5%，与其相邻的Y型节点的分支构件、X型节点的分支构件和屋盖桁架下部支承杆件的失效导致屈曲临界荷载分别降低约9.73%、9%和4.14%。说明Y型节点主干构件的失效对结构稳定性的影响最大，通过增强该树状结构主干可以提高结构的承载力。

图6 关键构件失效的屈曲荷载系数-竖向最大位移曲线Fig.6 Buckling load coefficient and vertical maximum displacement curve of key components failure

表7 关键构件失效下荷载屈曲系数Tab.7 Load buckling coefficient of key component failure

4 结论

1.利用ABAQUS和MIDAS 对结构进行线性屈曲分析发现，结构在第5 组荷载组合工况下屈曲荷载系数最小，可以作为最不利荷载组合工况。该工况下屈曲失稳主要发生在屋盖网架结构以及树状支承的前侧，其中以树状支承结构节点处更为明显。

2.对结构进行几何非线性屈曲分析发现，初始缺陷对结构几何非线性稳定承载力影响较小，承载力下降在5%～10%，说明该结构为缺陷不敏感结构。

3.对结构进行双重非线性屈曲分析发现，考虑几何、材料双重非线性相较于几何非线性，结构的屈曲荷载系数有明显下降。其中初始缺陷的变化使非线性稳定承载力降低8%～16%。

4.对结构关键构件失效的双重非线性屈曲分析发现，不同部位关键构件的失效均会影响结构受力性能，会使结构稳定性下降，其中以树状支承结构主要受力的Y型节点的主干失效对结构稳定性影响最大，通过增强该树状结构主干可以提高结构的承载力。