基于Open SEES的陶粒混凝土钢板组合剪力墙受力性能分析*
2021-09-06邵禹铭姬淑艳姜宝龙熊涛
邵禹铭 姬淑艳 姜宝龙 熊涛
1.重庆大学土木工程学院 400045
2.重庆大学管理科学与房地产学院 400045
3.金科集团股份有限公司 重庆401133
引言
陶粒混凝土具有质量轻、保温性能好、绿色节能的优点。陶粒混凝土钢板组合剪力墙是在双层钢板中间内填陶粒混凝土,通过设置对拉螺栓使得钢板与混凝土协同受力的新型抗侧力构件,既解决了模板的问题,又通过约束作用提高了陶粒混凝土的强度,弥补了其强度不足的劣势,使其能够在建筑领域中获得充分应用。
国内外学者对外包钢板普通混凝土组合剪力墙以及陶粒混凝土剪力墙展开了一系列研究:聂建国、樊健生[1-5]对外包钢板混凝土组合剪力墙进行了变参数的低周往复试验研究。张晓萌[6]对变参数的钢管束组合剪力墙进行了研究,研究得到其破坏模式、工作机理以及各参数对其受力性能的影响。程春兰[7]对带对拉螺栓的外包钢板混凝土组合剪力墙进行了试验和模拟研究,得出了轴压比、高宽比、螺栓间距对其受力性能影响显著。刘翠兰[8]对陶粒混凝土以及普通混凝土的剪力墙试件开展试验,证明了轴压比较低时,陶粒混凝土剪力墙可以满足剪力墙结构延性要求。Carrillo J[9]对轻质混凝土剪力墙构件进行了拟静力试验和结构体系振动台试验研究,试验结果表明轻质混凝土剪力墙的承载、变形、耗能能力在不同极限状态下优于普通混凝土剪力墙。李传浩和王二成[10]对槽钢骨架的轻质混凝土剪力墙进行了试验研究并验证了暗柱和暗支撑对其承载力和延性影响显著。
目前国内外研究主要集中在普通混凝土钢板组合剪力墙领域,对陶粒混凝土钢板组合剪力墙研究较少。本文利用Open SEES有限元模拟软件,建立陶粒混凝土钢板组合剪力墙,通过将分析结果对比试验数据[11]来验证数值模型的可靠性,并基于该有限元模型分析了轴压比、剪跨比、截面宽厚比以及钢板厚度对陶粒混凝土钢板组合剪力墙结构受力性能的影响。
1 试验概况
试验[11]试件为一字型截面,外包钢板中间内填混凝土,采用对拉螺栓施加约束作用,端部焊接方钢管混凝土柱,外包钢板与两端方钢管的钢板厚度同为2mm。墙顶施加恒定轴力,水平方向采取位移控制的方式进行低周往复加载。本文选取其中试件SW2 与试件SW6 进行模拟分析,二者几何尺寸均相同:墙体高度为1680mm,宽度为840mm,厚度为84mm,轴压比为0.2,二者分别内填陶粒混凝土与普通混凝土,其具体尺寸参数见图1。

图1 试件尺寸与构造(单位:mm)Fig.1 Specimen size and structure(unit:mm)
2 有限元模型
2.1 纤维截面
Open SEES是一款开源软件,其优越的精确度、强大的计算能力以及高效的运算效率令其目前在结构抗震领域应用广泛[12]。
本文采用纤维模型进行有限元模拟,纤维模型可以将截面划分为多个纤维并赋予各个纤维不同的材料本构关系,根据截面变形情况得到各纤维的应力应变从而确定截面受力特性。针对纤维模型不能考虑剪切变形的劣势,本文采用Open SEES平台开发出的section Aggregator 剪切子单元[13],定义一种单轴材料对纤维截面的非线性剪切应力应变进行模拟,随后将该定义的材料组合到纤维截面上即可实现对剪切变形影响的考虑,最终通过定义各类控制参数,将其等效为考虑了剪切变形效应的剪切材料。
2.2 材料本构
本文采用Concrete02 材料[14]对陶粒混凝土和普通混凝土进行模拟。其受压应力应变骨架曲线为Kent-Park模型,如图2 所示。
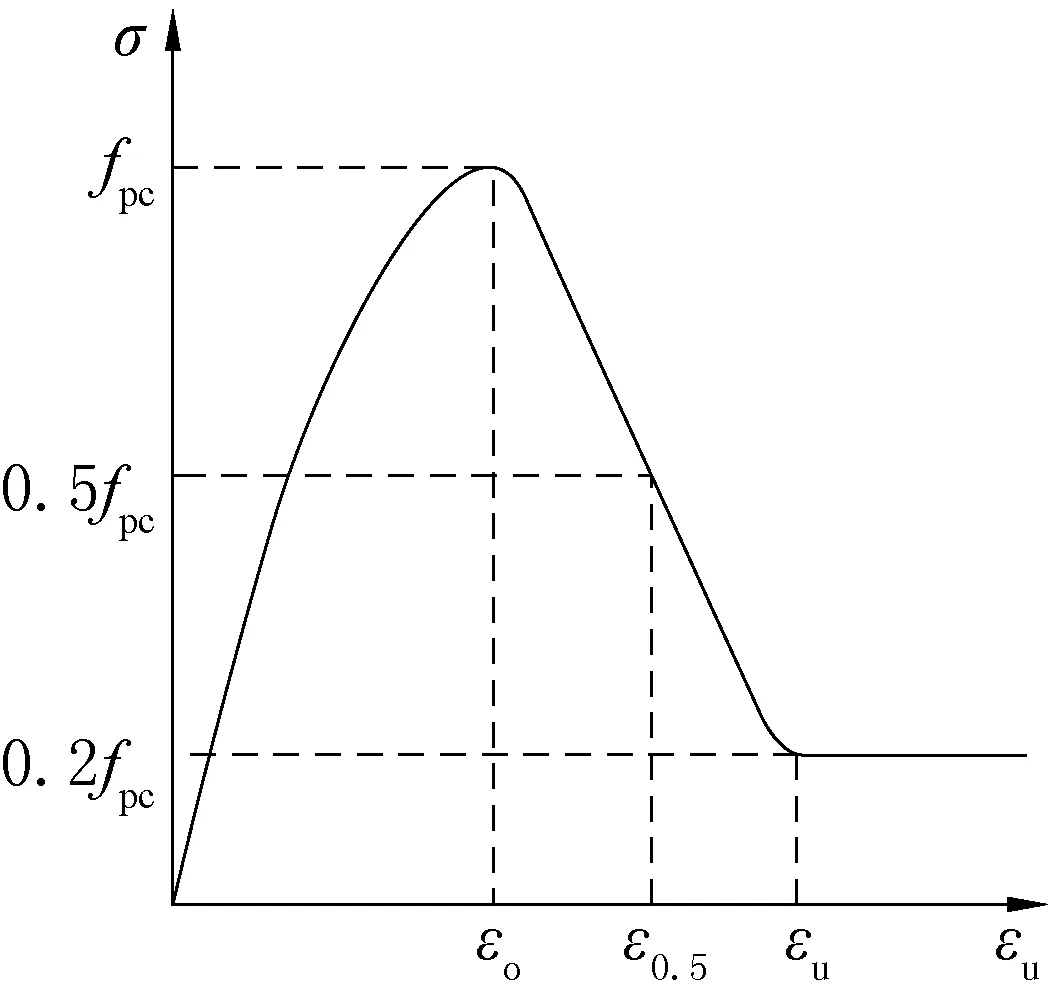
图2 混凝土Kent-Park 本构模型曲线Fig.2 Kent-Park constitutive model curve
由于陶粒是多孔脆性材料,以其为骨料的陶粒混凝土强度较低,延性较差,在本构曲线中表现为在上升段峰值荷载出现较晚,而下降段承载力跌落较快。在Open SEES 中,可以通过设置参数特征点(峰值点、下降段中点、平台段起点)来将二者区分开:普通混凝土特征点可按照《混凝土结构设计规范》(GB50010—2010)确定,陶粒混凝土可按已有的研究成果[15,16]取值。对应的本构曲线如图3 所示。
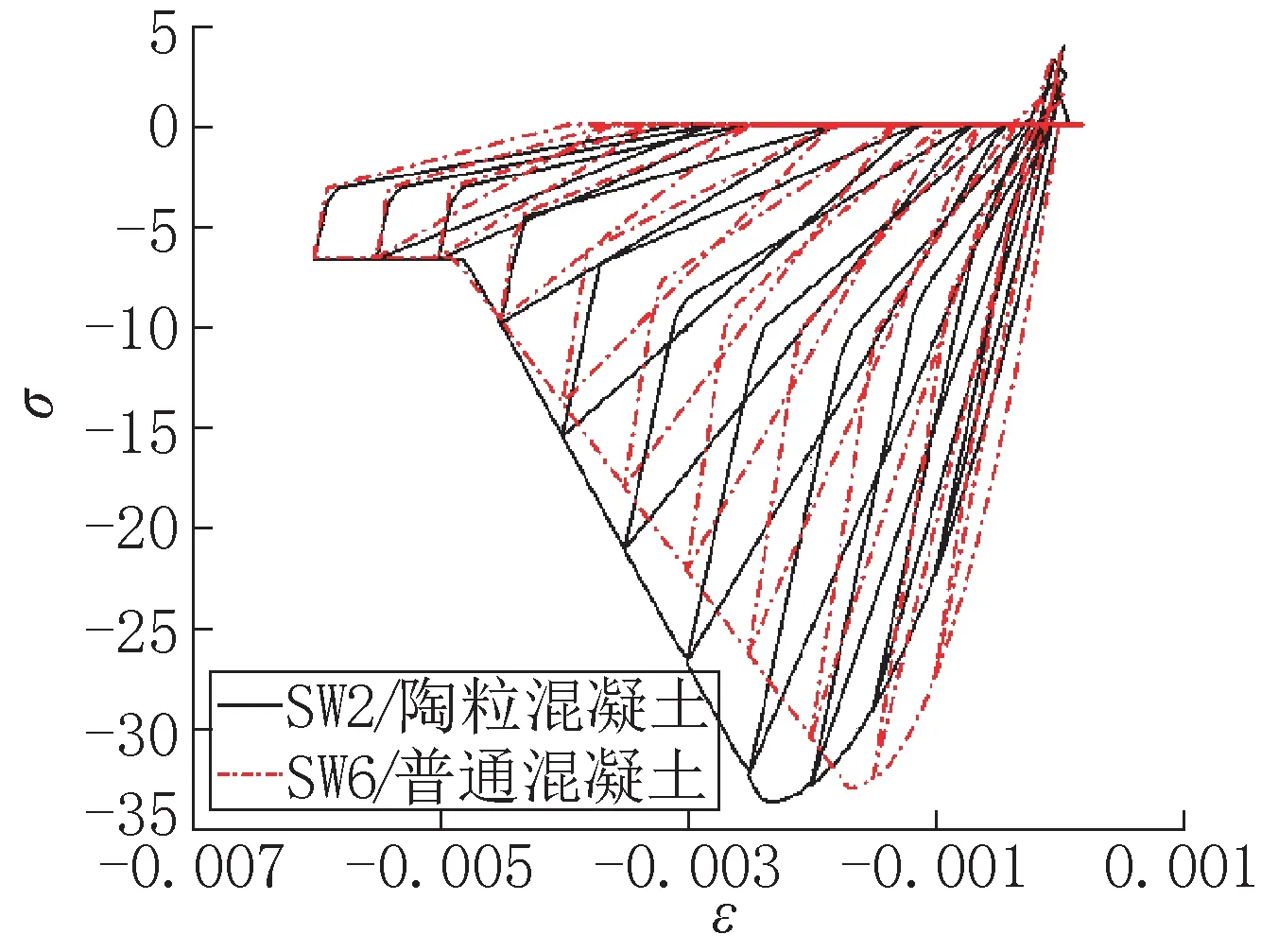
图3 混凝土材料在往复荷载作用下应力应变曲线Fig.3 Stress strain curve of concrete material under reciprocating load
同时,由于两端方钢管柱的约束作用以及在螺栓对拉作用下外包钢板对内部混凝土材料的约束作用,本文根据Kent-Park 约束混凝土模型[14]及试验数据,设置了参数k1作为混凝土材料强度的提高系数,设置参数k2作为混凝土材料极限压应变的提高系数,以此来提高对其滞回性能模拟的精确度,根据不同构件材料性能的差异,对试件SW2 的k1取1.21,k2取1.366;对试件SW6 的k1取1.19,k2取1.393。
钢材的本构关系采用Filippou[17]等学者提出的钢材拉伸强化研究理论的Steel02 材料。如图4所示,在考虑等向应变硬化作用效应的基础上,通过参数调整弹塑性段分支点处的弧度,达到考虑包辛格效应的目的。
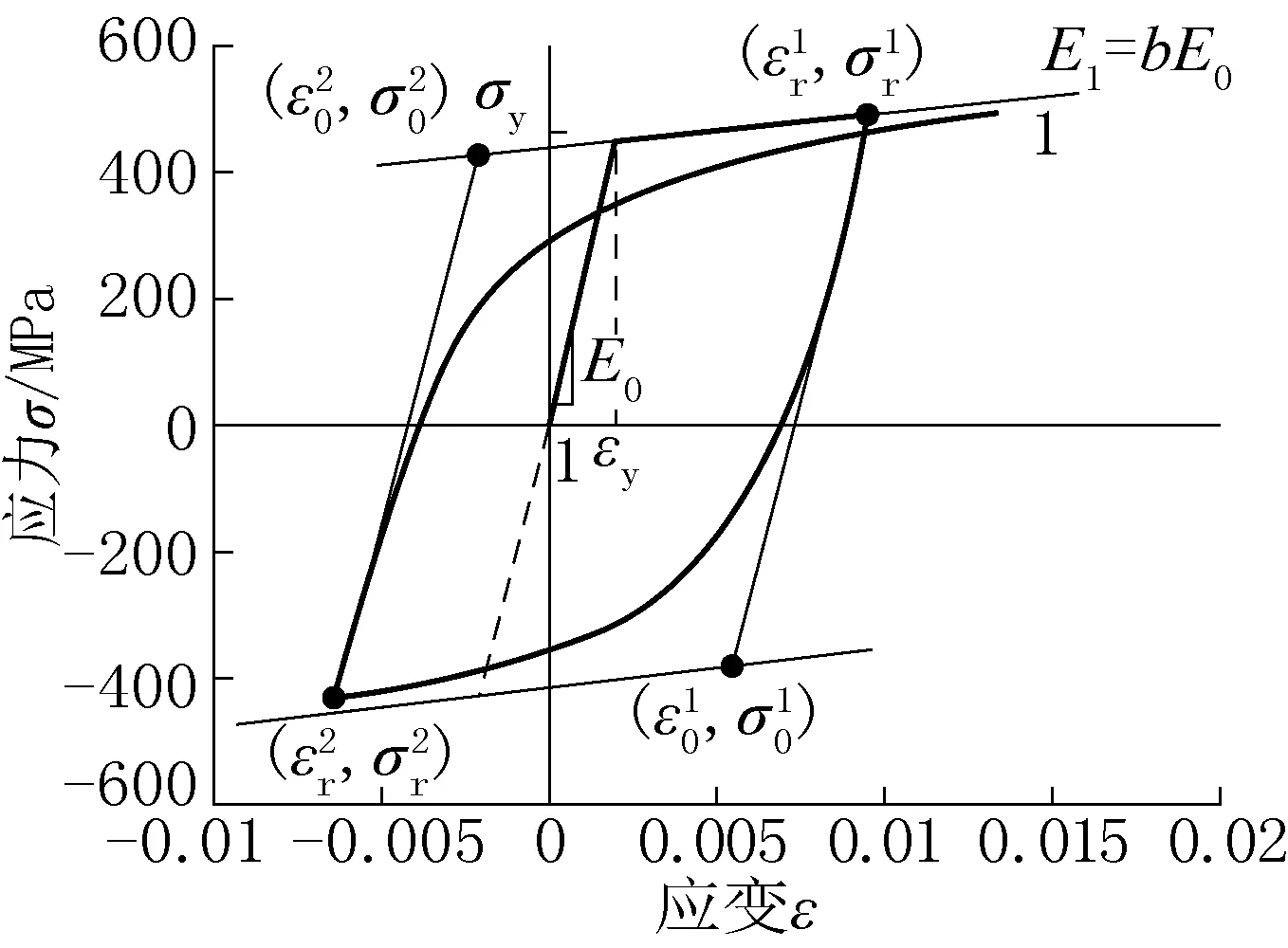
图4 Steel02 Material 应力应变曲线Fig.4 Stress strain curve of Steel02 Material
3 数值模拟有效性校核及分析
建立有限元模型,模拟计算试件SW2 和SW6 的滞回曲线及骨架曲线,并与试验结果比较,如图5、图6 所示。
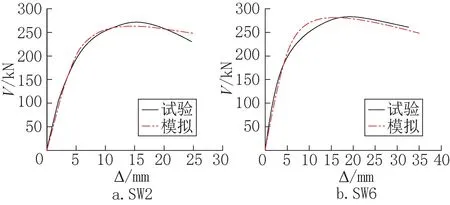
图6 骨架曲线的对比Fig.6 Comparison of skeleton curves
由图5 滞回曲线对比可以观察到,两者计算结果总体接近,验证了数值分析中选取截面及本构关系的合理性,但SW2 的滞回曲线模拟结果与试验结果存在一定差距。其主要不同点及原因如下:首先,模拟结果具有较大的初始刚度,这是因为在试验加载过程中陶粒混凝土与钢板存在较大的粘结滑移破坏,使得二者共同工作机制减弱,结构耗能能力降低,而模拟计算是假定钢板与混凝土共同工作的,无粘结滑移,同时,试验过程中试件存在微小拔出,可见试验基础梁并非理想的无限刚度构件,而模拟试件底部为全部固结设置,这均导致模拟结果的初始刚度较大;其次,峰值荷载后的模拟值大于试验值,无明显承载力下降,这是因为用于模拟计算的叠加剪切单元的纤维模型截面受剪效应无法充分反映实际材料的损伤状况及钢板屈曲的影响,目前其余分析方法同样无法充分反映剪力墙加载过程中的剪切效应,因此针对以压弯破坏为主的该构件采用该模型进行模拟仍是可行的。
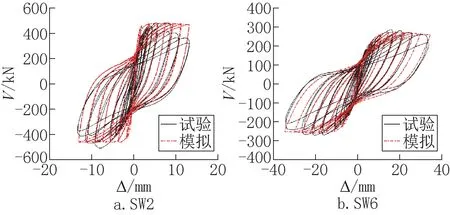
图5 滞回曲线的对比Fig.5 Comparison of hysteretic loop
从图6 骨架曲线对比可以观察到,数值模拟结果与试验结果是总体接近的,尤其在弹性阶段能够较好吻合,而在塑性阶段模拟结果与实际结果的不同点及原因如下:首先,SW2 模拟结果的峰值荷载较小,这可能是由于混凝土材料强度具有离散性,试验墙体混凝土材料强度相比材性试块材料强度更大导致的;同时,模拟结果的峰值荷载相比试验值更早出现,即峰值位移较小,这是由于模拟计算中假定钢板与混凝土共同工作、无粘结滑移所致;另外数值模拟骨架曲线的下降段相较试验值更为平缓,承载力退化不明显,这可能是由于模拟中未考虑螺栓破坏及钢板局部屈曲的影响,导致SW2 模拟结果的剪力墙后期承载力相比试验值较高。总体而言,数值计算结果与试验结果的误差较小,采用Open SEES 对陶粒混凝土钢板组合剪力墙结构的受力性能模拟是可靠的。
本文采用作图法[18]确定模拟结果的屈服荷载及屈服位移,根据骨架曲线峰值点定义极限荷载和极限位移,计算结果见表1,总体而言,陶粒混凝土试件滞回曲线饱满,具有较强的耗能能力,其承载力略低于普通混凝土试件,且峰值荷载出现较早,承载力退化速度更为迅速。
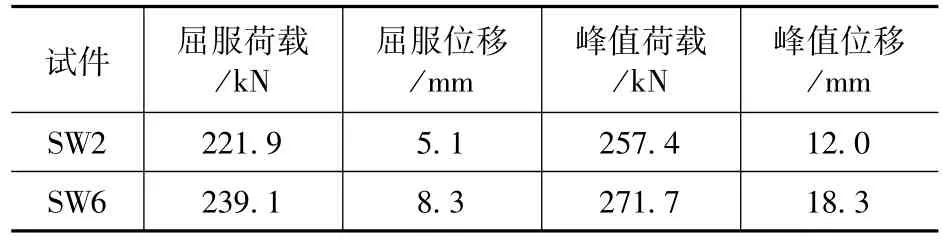
表1 构件特征值对比Tab.1 Comparison of component eigenvalues
4 参数影响分析
采用上述方法建立陶粒混凝土钢板组合剪力墙模型SY1~SY4、SJ1~SJ6、SK1~SK4、SG1~SG4,对其施加低周往复荷载,以刚度、承载力、延性为性能指标,分析轴压比、剪跨比、截面宽厚比与钢板厚度对陶粒混凝土钢板组合剪力墙受力性能的影响。
4.1 轴压比
为研究轴压比对陶粒混凝土钢板组合剪力墙受力性能的影响,以试件SW2 为基础,保持其他参数均不变,新增设计4 个试件SY1 至SY4。试件SY1、SW2、SY2、SY3、SY4 轴压比依次为0.1~0.5。计算结果见表2,特征值及骨架曲线对比情况见图7。可以看出,试件在加载过程中,其前期刚度受轴压比影响较小;当轴压比小于0.4 时,随着轴压比增大,构件在屈服阶段的承载力逐渐上升,以SY1(轴压比0.1)为基准,增幅依次为9.7%、15.0%、16.3%,上升趋势渐缓,在轴压比为0.4 时,承载力达到最大值,轴压比为0.5 时,承载力略有下降。
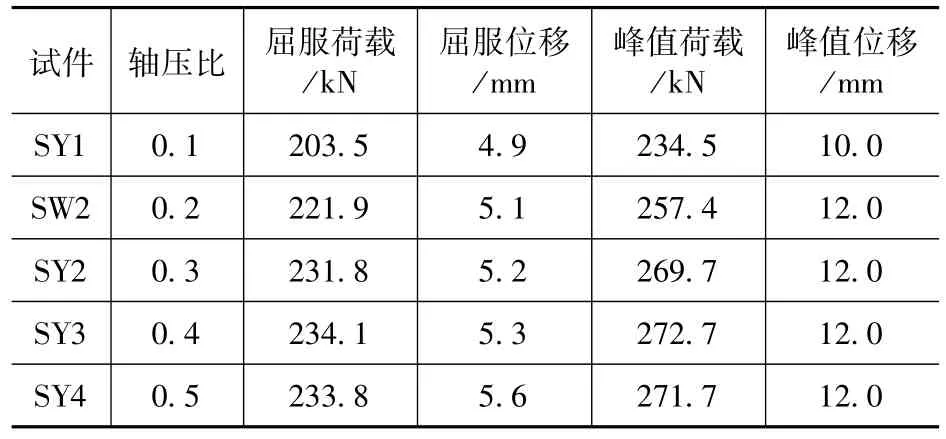
表2 变轴压比计算结果Tab 2 Calculation results of variable axial compression ratio
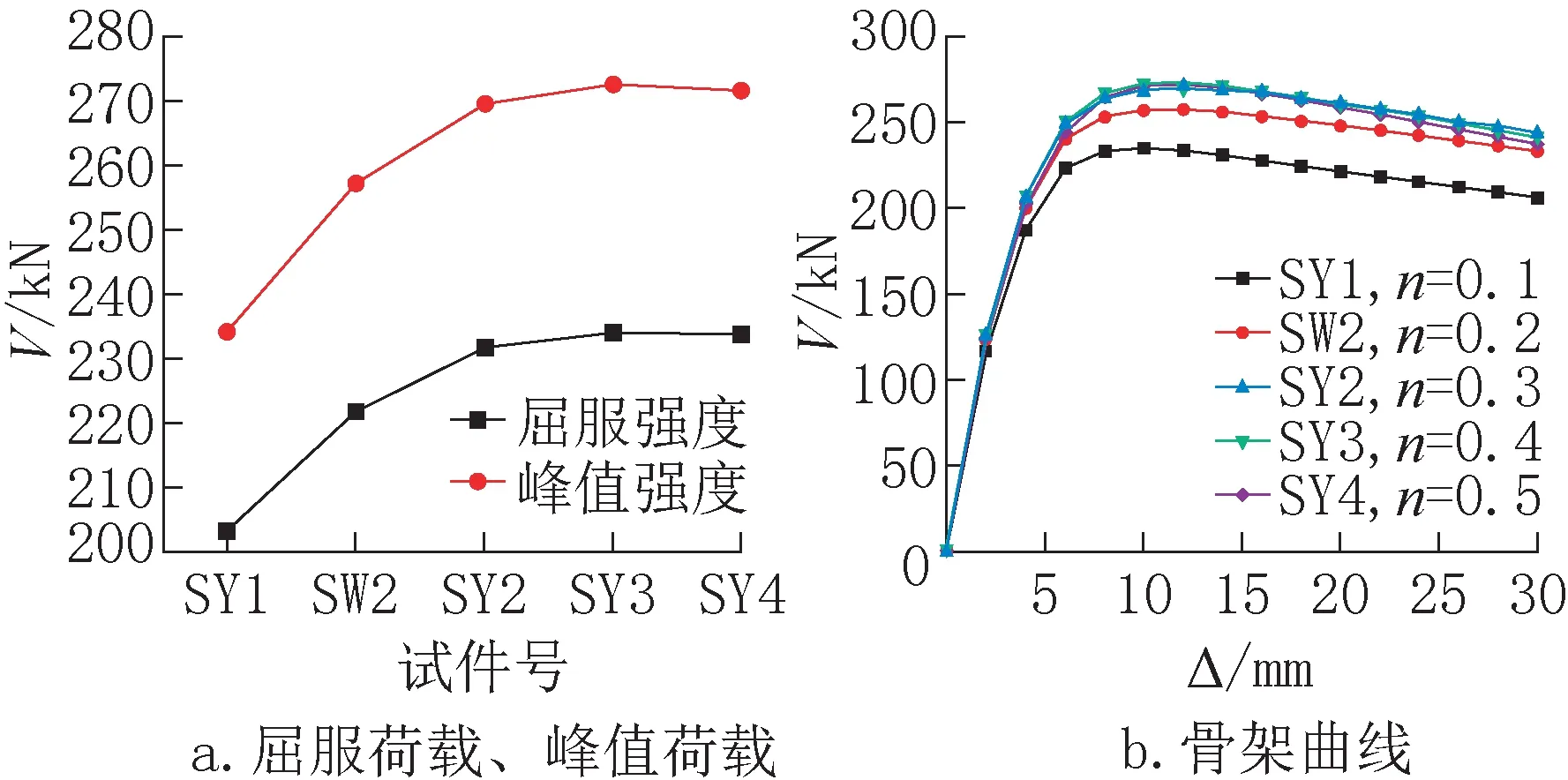
图7 特征值及骨架曲线对比Fig.7 Comparison of eigenvalues and skeleton curves
4.2 剪跨比
以试件SW2 为基础,保持其他参数均不变,新增设计6 个试件,编号SJ1 至SJ6。试件SJ1、SJ2、SJ3、SJ4、SW2、SJ5、SJ6 的剪跨比依次为1.0、1.25、1.5、1.75、2.0、2.25、2.5,计算结果见表3,特征值与骨架曲线对比见图8。可以看出,随着剪跨比减小,试件的初始刚度和承载力逐渐降低;以SJ1(剪跨比1.0)为基准,峰值荷载降幅依次为16.1%、30.1%、40.3%、47.9%、53.8%、58.6%,从特征值对比图可见,其峰值荷载的降低是近线性的;剪跨比小于2 时,随着剪跨比增大,构件承载力退化速度减慢,延性增强,超过这一限值后,随着剪跨比增大,构件延性基本不变。
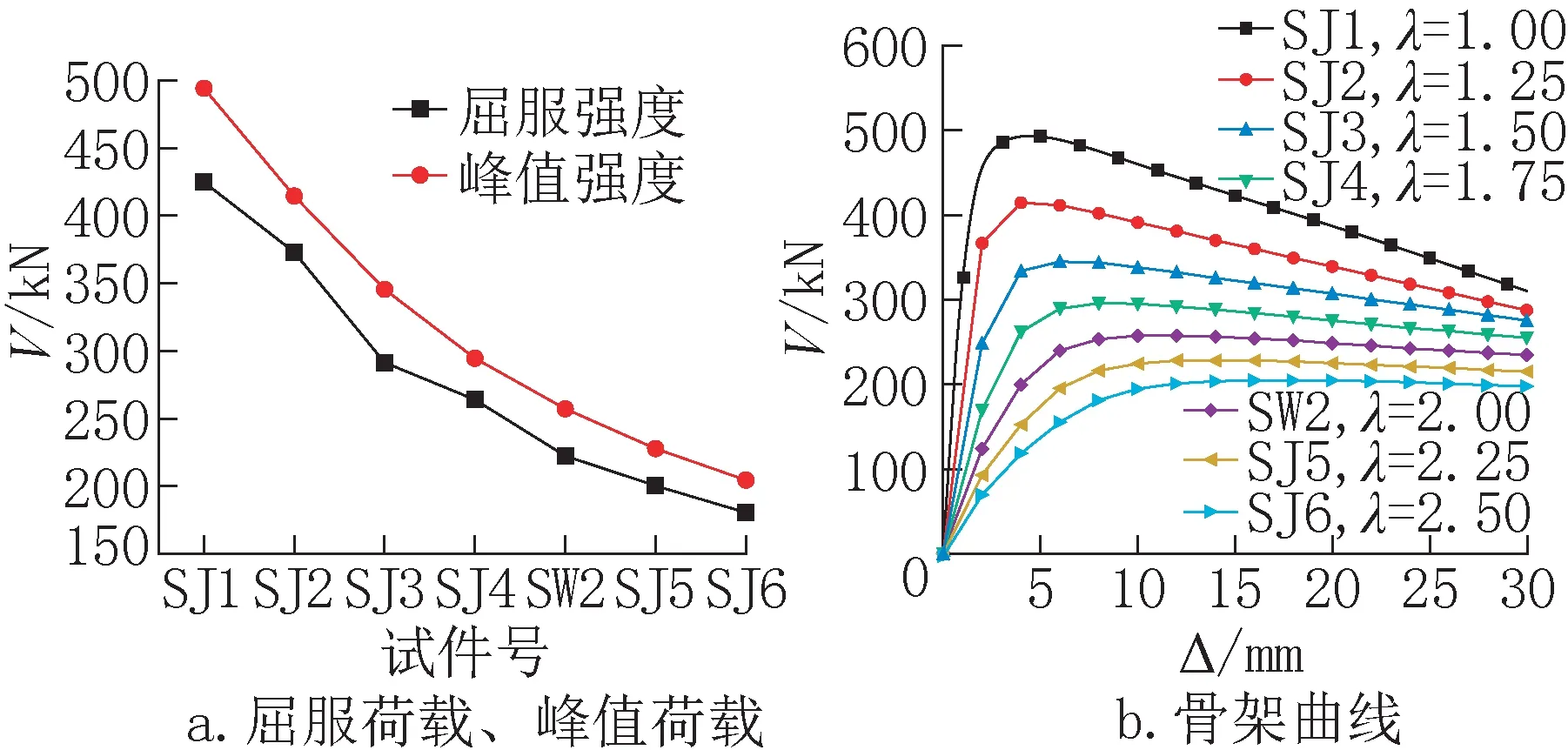
图8 特征值及λ 骨架曲线对比Fig.8 Comparison of eigenvalues and skeleton curves
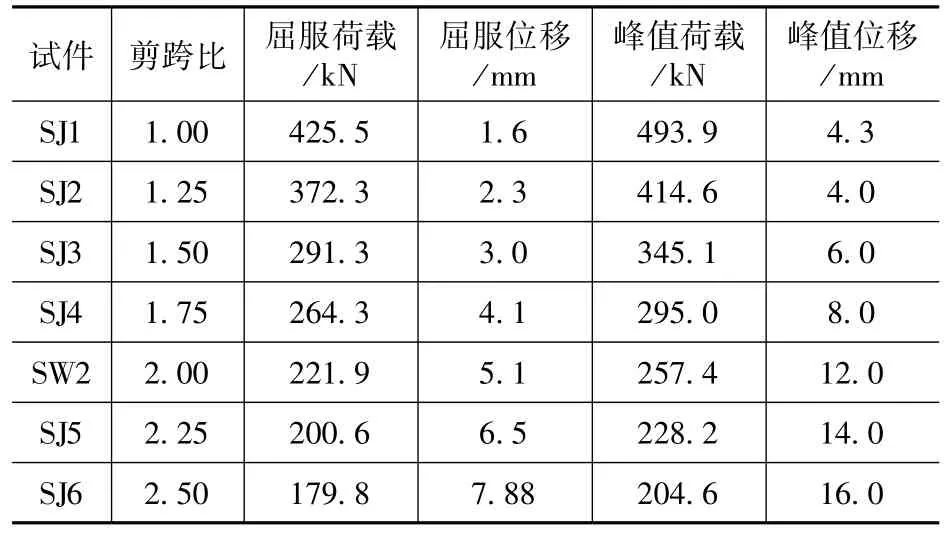
表3 变剪跨比计算结果Tab 3 Calculation results of variable shear span ratio
4.3 截面宽厚比
以试件SW2为基础,保持其他参数均不变,改变截面陶粒混凝土层的厚度,新增设计4 个试件,编号SK1 至SK4,试件SW2、SK1、SK2、SK3、SK4 墙体厚度依次为84mm、98mm、112mm、126mm、140mm,计算结果见表4,特征值及骨架曲线对比见图9。可以观察到,随着墙体厚度增加,构件初始刚度上升;以SW2(墙厚84mm)为基准,随着墙体厚度增加,承载力增幅依次为9.2%、17.9%、26.6%、35.1%,其他条件不变的情况下,每增加14mm 陶粒混凝土墙体厚度,承载力增幅约为9%,呈线性增长;构件承载力退化速度不受墙体厚度影响,随墙厚增加构件延性基本保持不变。
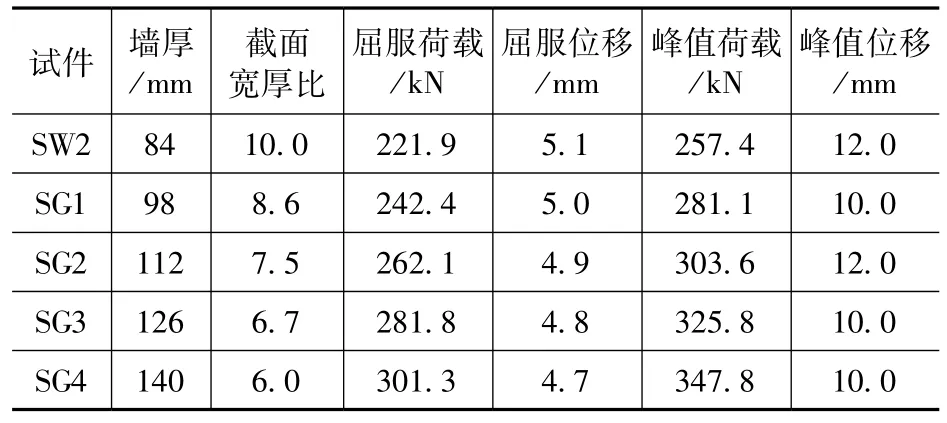
表4 变截面宽厚比计算结果Tab.4 calculation results of variable section width thickness ratio
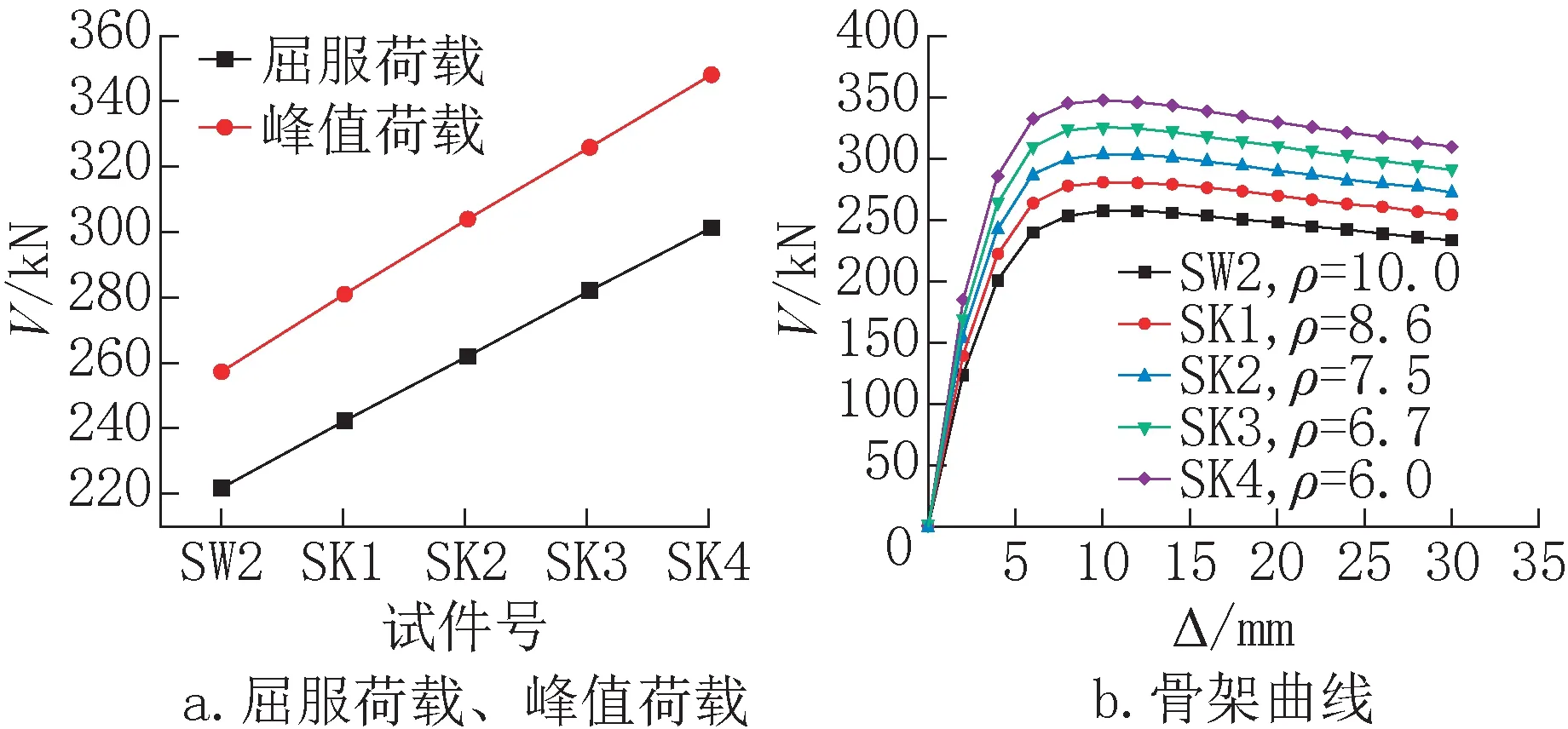
图9 特征值及骨架曲线对比Fig.9 Comparison of eigenvalues and skeleton curves
4.4 钢板厚度
由于本批次构件未设置加劲肋,截面配钢率可以用钢板厚度进行表征。以试件SW2 为基础,保持其他参数均不变,新增设计4 个试件,编号SG1 至SG4。试件SW2、SG1、SG2、SG3、SG4的钢板厚度分别为:截面所有钢板均为2mm、3mm、4mm、中部外包钢板厚度2mm +方钢管钢板厚度3mm(2mm +3mm)、中部外包钢板厚度2mm +方钢管钢板厚度4mm(2mm +4mm),计算结果见表5,特征值与骨架曲线对比见图10。可以看出,以SW2(截面配钢率5.7%)为基准,截面所有钢板厚度每增加1mm,构件承载力增幅依次为24.9%、46.3%,每增加1mm 截面所有钢板厚度,承载力增幅约为23%,呈线性增长,可见钢板厚度增加对构件承载力的提升效果是十分显著的;随着截面所有钢板厚度增加,承载力退化速度加快,延性降低;试件SG4 截面配钢率低于试件SG1,但水平承载力相近,可以得出相对于改变截面所有钢板厚度,局部增加端部方钢管的钢板厚度对构件水平承载力增强效果更为显著,可见边缘构件在抗侧向力方面有较大贡献。
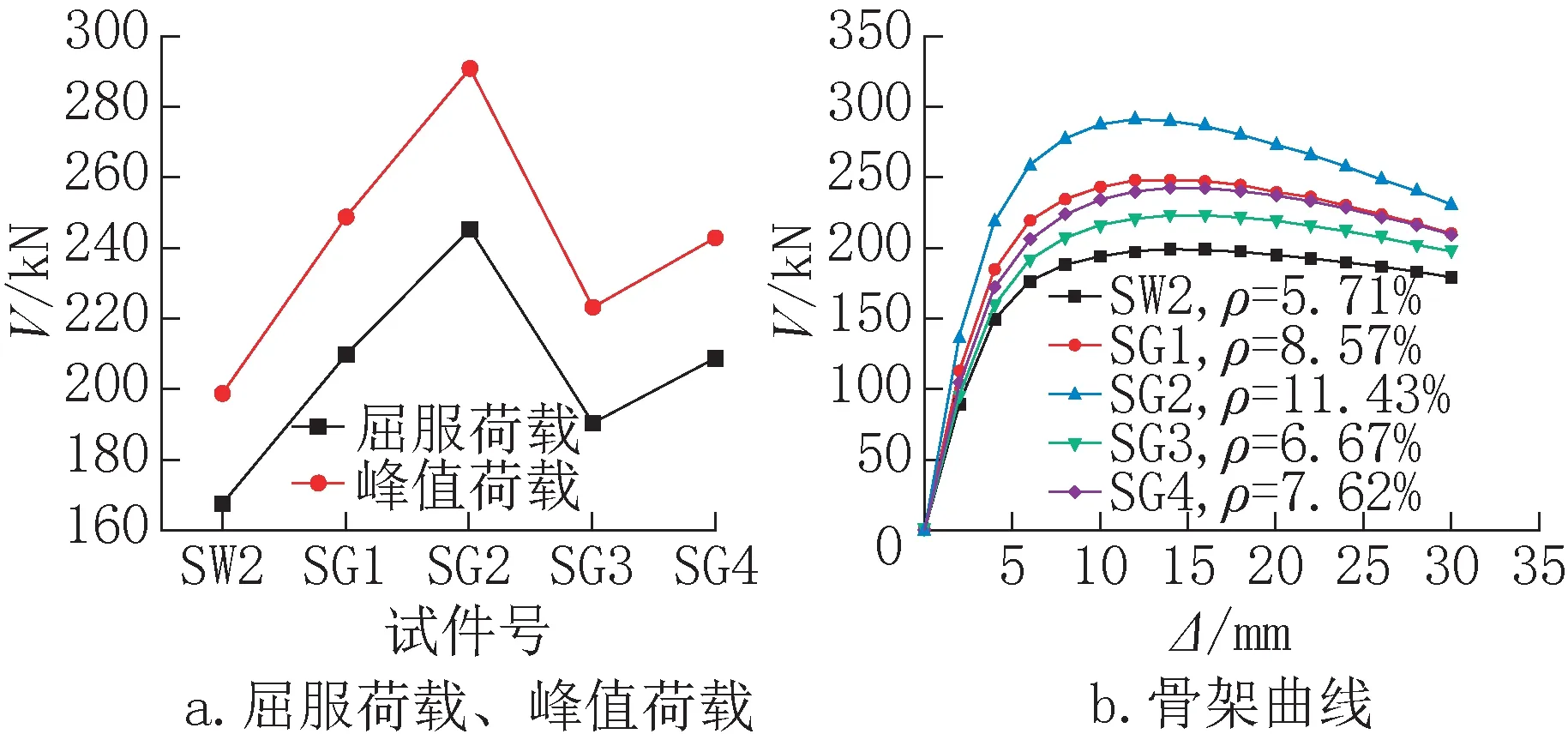
图10 特征值及骨架曲线对比Fig.10 Comparison of eigenvalues and skeleton curves
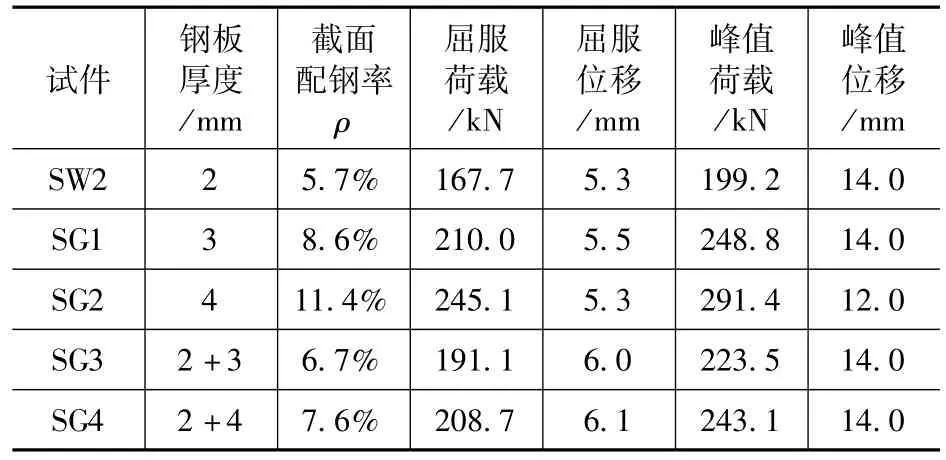
表5 变钢板厚度计算结果Tab 5 Calculation results of variable plate thickness
5 结论
采用Open SEES 有限元软件建立纤维模型,对陶粒混凝土钢板组合剪力墙在低周往复荷载作用下的全过程进行模拟,通过对比数值计算结果和试验结果并进行参数化分析,得到以下结论。
1.采用Open SEES 计算分析所得滞回曲线、骨架曲线与试验所得结果拟合较好,验证了所建模型的可靠性,表明Open SEES 能够比较准确地模拟出陶粒混凝土薄钢板组合剪力墙的受力性能,可以为其设计分析提供有效支持。
2.当轴压比小于0.4 时,陶粒混凝土钢板组合剪力墙的水平承载力随轴压比增大而增加,并在轴压比为0.4 时获得最大承载力,之后随着轴压比增大,构件承载力开始下降。
3.陶粒混凝土钢板组合剪力墙承载力随剪跨比增大而近线性降低,剪跨比小于2 时,构件延性随剪跨比增大而上升,剪跨比大于2 后,随着剪跨比增加,构件延性基本保持不变。
4.随着陶粒混凝土钢板剪力墙截面宽厚比降低,构件承载力线性增加,陶粒混凝土墙体厚度每增加14mm,水平承载力增幅约9%,构件延性基本保持不变。
5.增大截面钢板厚度可以显著提升陶粒混凝土钢板组合剪力墙的受力性能,截面所有钢板厚度每增加1mm,水平承载力增幅约23%,增大端柱方钢管的钢板厚度对承载力提升更优。
