基于有限元法和一次二阶矩法的桥梁结构可靠度研究

王虎军 贺小卫 高宇 扈轩诚

西安市政设计研究院有限公司 710068

引言

以概率论和数理统计为基础的可靠度计算方法，如中心点法、验算点法、JC 法、MC 法、响应面法等可为桥梁结构的可靠性评估提供便利。但由于实际桥梁结构体系复杂，基于抗力—荷载效应的结构功能函数可能高度非线性，甚至不能显式表达。这就使得以功能函数的解析表达式为基础的中心点法、验算点法、JC法和MC法计算结构可靠度变得困难，甚至无法进行下去。响应面法虽然能够用一个简单的函数拟合隐含、复杂的真实功能函数，但当随机变量较多时，目前采用的多项式形式的响应面函数的系数计算工作量大且拟合误差大而变得不适用。

本文结合确定性有限元法和可靠度计算中改进的一次二阶矩法，在不必求得结构功能函数明确表达式的情况下，进行结构可靠指标的分析计算，通过MATLAB编程，计算了一钢管混凝土拱桥纵梁跨中截面正常使用极限状态下的可靠度指标，并对各随机变量灵敏度进行分析，为结构设计中提高可靠度给出了方向。

1 改进的一次二阶矩法

改进的一次二阶矩法是将功能函数的线性化展开点选在失效的边界Z＝0 上，而且选在结构最大可能失效概率的点上，故又称设计验算点法。其计算原理在文献［11］中有详细论述，在此不再累述。设结构的功能函数为Z＝Z（X1，X2，X3，…Xn），其中Xi（i＝1，2，3…n）为随机变量，如结构几何尺寸、材料物理参数及外荷载等，且各随机变量间相互独立，则改进的一次二阶矩法的迭代计算步骤如下：

2 有限元法与改进的一次二阶矩法的结合

基于抗力—荷载效应的结构功能函数中，荷载效应通常为几何尺寸、荷载、弹性模量、泊松比等随机变量的隐式函数，即S＝S（X1，X2，X3，…Xn），其中Xi（i＝1，2，3…n）为各随机变量。而抗力R则通常为规定的一限值或具有明确表达式，则结构的功能函数可表示为Z＝R－S。设各随机变量的分布类型已知，则可根据改进的一次二阶矩法迭代求解可靠指标和验算点，由于功能函数中荷载效应不能显式表达，导致无法直接计算功能函数在验算点处的偏导数，本文利用有限元法的数值模拟功能及数值分析中的向前差分法［2］很好地解决了偏导数的求解问题，即：

3 工程实例

3.1 工程概况及有限元建模

某中承式钢管混凝土拱桥，计算跨径为260m，计算矢跨比1／4，拱轴线为悬链线，拱轴系数m＝1.5。拱肋为四肢钢管混凝土桁架结构，上下弦杆为平放的哑铃型断面。拱肋由外径950mm的Q345Dq螺旋焊管及其内填充的C50 混凝土组成，截面总高5.35m，总宽2.75m；吊杆采用OVM.GJ15-15 拉索，横向双吊杆体系，纵向间距10m，横向间距0.4m ＋18.5m ＋0.4m；横梁全桥共设置29 道（19 道吊杆横梁＋2 道拱上横梁＋8 道立柱横梁），吊杆横梁为等高度预制“Ⅰ”字型梁，高1.8m；桥面系采用吊杆横梁上设置纵向“T”型行车道梁，预制施工，梁高0.7m，腹板宽0.2m，翼缘宽1m，纵向长10m；桥面铺装采用10cm 厚聚酯纤维沥青混凝土，设置1.5%的双向横坡和3%的双向纵坡。

采用大型通用有限元分析软件Midas Civil建立全桥模型。钢管混凝土拱肋、拱上横撑、横梁、拱上立柱、行车道板均为梁单元；吊杆采用桁架单元；拱脚位置处用一般支撑中约束所有自由度模拟。全桥共离散为4654个节点和5460个单元。实桥有限元模型见图2。

图2 实桥有限元模型Fig.2 Finite element model of real bridge

3.2 结构可靠度分析

采用规范规定的挠度限值作为钢管混凝土拱桥正常使用极限状态下的失效准则，以钢管混凝土拱桥纵梁跨中挠度超过限值uL为主要失效模式，根据《公路钢管混凝土拱桥设计规范》（JTG／T D65—2015）计算得uL＝0.325m，建立结构正常使用极限状态功能函数Z为：

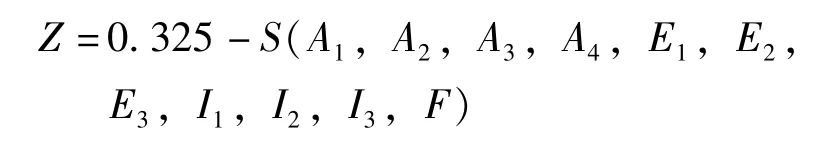
式中：A1为拱肋截面面积；A2为吊杆截面面积；A3为横梁截面面积；A4为纵梁截面面积；E1为Q345Dq 钢弹性模量；E2为C50 混凝土弹性模量；E3为拉索钢绞线弹性模量；I1为拱肋截面惯性矩；I2为横梁截面惯性矩；I3为纵梁截面惯性矩；F为活载。

各参数的分布类型、均值、变异系数主要参照实桥检测结果，并结合《公路工程结构可靠度设计统一标准》及相关文献确定，见表1。

表1 各随机变量的统计参数Tab.1 Statistical parameters of random variables

按图1 迭代步骤进行迭代计算，共迭代16次满足规定的误差要求，有限元计算171 次。部分迭代结果见表2。

图1 有限元与改进的一次二阶矩法结合解算流程Fig.1 Flow chart of the combination of finite element and improved first order second moment method

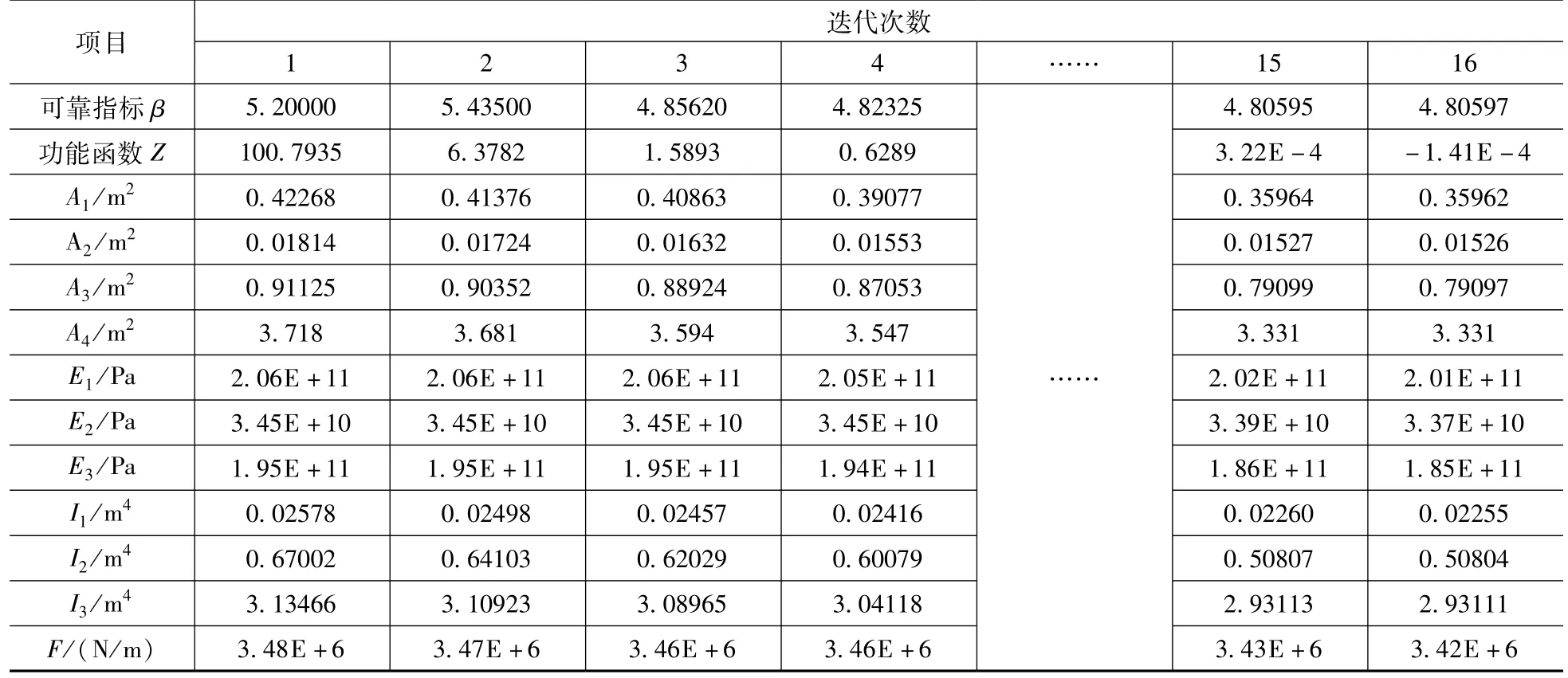
表2 迭代计算过程Tab.2 Iterative calculation process

钢管混凝土拱桥在设计过程中，材料性能和几何参数等不确定性因素势必对结构可靠性产生 影响，为了准确掌握各随机变量对结构可靠度指标的影响程度，对钢管混凝土拱桥各随机变量进行灵敏性分析，给出了各随机变量重要性程度的比较值，如表3 所示。

表3 各随机变量的灵敏度系数Tab.3 Sensitivity coefficient of each random variable

为了更直观地分析各随机变量对结构可靠指标的影响程度，将各随机变量的灵敏度值的绝对值进行比较，如图3 所示。

图3 各随机变量灵敏度绝对值比较Fig.3 Comparison of sensitivity absolute value of each random variable

由表3 及图3 可见，拱肋面积A1的灵敏度最大为0.925，对结构可靠指标的影响最大，纵梁截面面积A4的灵敏度绝对值最小为0.014，对可靠指标影响较小，实际计算时可不考虑其影响。

4 结语

本文以实桥工程为依托，采用有限元法和改进的一次二阶矩法相结合的方法对其可靠度进行研究，验证了该方法的可行性，并通过各随机变量对结构可靠指标的灵敏度分析，得到各随机变量对结构可靠性的影响程度，为结构的优化设计提供方向。