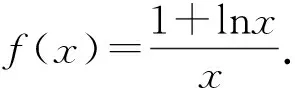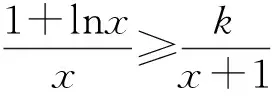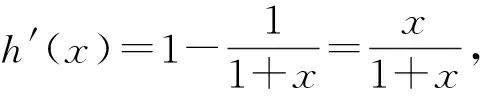用构造法求恒不等式中的参数范围
2021-09-06福建省龙岩市长汀县第一中学366313周兴腾
福建省龙岩市长汀县第一中学 (366313) 周兴腾
在许多高考题或高考模拟题中,导数的综合题往往都是把关的角色,其中恒成立问题中求参数范围的题目更是内容丰富、形式多样,而我们有些同学也经常是止步于此,究其原因是缺少破题方法.而因题而异、深挖内含是非常重要的,其中抓住题设特点,通过构造新函数求解此类问题就是一个有效的举措.本文举例介绍几种常见的使用方法,供参考.
一、移项后构造
通过把题设的恒不等式移项处理,变成一边为零后,直接构造函数.
例1 设函数f(x)=x(ex-1)-ax2.若当x≥0时,恒有f(x)≥0,求a的取值范围.
解析:由于f(x)=x(ex-1-ax),当x≥0时,f(x)≥0等价于ex-1-ax≥0,令g(x)=ex-1-ax,则g′(x)=ex-a.若a≤1,则当x∈(0,+∞)时,g′(x)>0,g(x)为增函数,而g(0)=0,从而当x≥0时,g(x)≥0,即f(x)≥0.若a>1,则当x∈(0,lna)时,g′(x)<0,g(x)为减函数,而g(0)=0,从而当x∈(0,lna)时,g(x)<0,即f(x)<0.综合得a的取值范围为(-∞,1].
评析:将不等式转化为一个函数式恒大于零(或恒小于零)后,如果通过求导数能够解决参数范围的,就不需要再进行其他变形,否则可能将问题复杂化.
例2 设函数f(x)=(x+1)1n(x+1),若对所有的x≥0,都有f(x)≥ax成立,求实数a的取值范围.
解析:设g(x)=(x+1)1n(x+1)-ax,其中x∈(-1,+∞).对函数g(x)求导得g′(x)=1n(1+x)+1-a.令g′(x)=0,解得x=ea-1-1.
①当a≤1时,对任意的x≥0,g′(x)>0,所以g(x)在[0,+∞)上是增函数,又g(0)=0,所以对所有的x≥0,都有g(x)≥g(0),即当a≤1时,对任意的x≥0都有f(x)≥ax.
②当a>1时,对于0
评注:将不等式恒成立转化为函数式恒大于零是解题的关键所在.后面再根据解题需要,通过求导、分类讨论的方法判断不等式是否成立,从而确定了参数的范围.
二、参数分离后构造
通过分离参数,可将恒不等式问题转化为求函数的最大值或最小值问题,使后续的解题方向非常清晰.
例3 已知f(x)=xlnx,g(x)=-x2+ax-3.若对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围.

评注:在解题中首先对不等式进行适当变形后,再通过设新函数利用导数解决问题,而变形的目的是分离变量,把参数分离后就可以利用求函数最值解决问题了.
例4 设函数f(x)=kx3-3x+1(x∈R),若对于任意x∈[-1,1],都有f(x)≥0成立,求实数k的取值范围.

评注:由于所给的自变量x的符号不能确定,所以必须通过分类讨论完成分离参数问题.
三、代数变形后构造
有些问题在运用直接求导和分离参数的方法后效果不理想,可以对所给的恒不等式进行适当的代数变形,然后再构造函数新函数解题.
例5 已知函数f(x)=x2ex,g(x)=1-ax.若当x≥0时f(x)≥x2g(x)恒成立,求实数a的取值范围.
解析:由f(x)≥x2g(x)得x2(ex-1+ax)≥0,当x≥0时f(x)≥x2g(x)恒成立,就是ex-1+ax≥0恒成立.设h(x)=ex-1+ax(x≥0),由于h′(x)=ex+a,当a≥-1时,h′(x)≥0对x≥0恒成立,所以h(x)≥h(0)=0,符合题意.当a<-1时,由h′(x)>0得x>ln(-a),由h′(x)<0,得0≤x 评注:解题中通过对恒成立不等式进行整理变形后,等价转化为另一个不等式,使问题变得简单得多了,这也是提高解题效率的重要方法之一. 例6 当x≥0时,不等式ax2-ex≤-x-1恒成立,求实数a的取值范围. 评注:在解本题中的构造更具有创造性,是在对参数进行分段后进行的,并且将指数问题转化为对数问题,为后面的大小比较、研究函数的单调性提供了最大帮助. 在用导数求函数最值时,许多情况下可能出现一次求导不能解决问题,还需要再一次求导才能确定函数单调情况,确定函数的最值. 评注:在本题中由于第一次构建的函数g(x)的单调性根据现有条件无法确定,故而再一次地构建一个新函数h(x),通过求导判断h(x)的单调情况,进而才能使问题获得解决. 例8 已知函数f(x)=x-ln(x+1), 若对任意的x∈[0,+∞),都有f(x)≤kx2成立,求实数k的取值范围. 评注:在解题中有两处构造,都是为了求导后方便比较大小而为之,其实质是将不等式的条件转化为含参数的函数单调性问题,通过分段讨论,使问题获得圆满解决.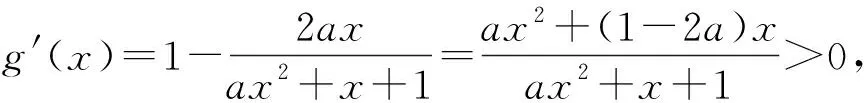
四、多次构造