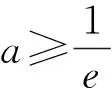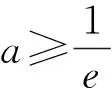两个重要恒等式在同构法中的应用

广东省佛山市第一中学 (528000) 刘振兴

在解决指对数混合不等式时，如恒成立求参数取值范围或证明不等式，如果用隐零点代换或某种意义上求根，计算复杂，同构法会给我们的解题带来极大的便利.在成立或恒成立问题中，有一部分试题是命题者利用函数单调性构造出来的，如果我们能找到这个函数模型(即不等式两边对应的同一函数)，无疑大大加快解决问题速度，找到这个函数模型的方法，我们称为同构法.

先来看2021年广东四校联考第22题.

(1)若m=1,x∈R,求函数g(x)=f(x)+f(-x)的最小值；

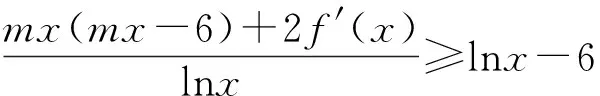
证明：(1)略.

(法二)法一中的等价变换也可以如下变化：

评注：本题学生得分很低，很多学生对同构法不熟悉，不会应用.法一中①式利用了恒等式a=elna，法二中②式利用了恒等式a=lnea，这两个恒等式也是在指对数同构中经常用到的恒等式.

在处理具体指对数同构题时，利用恒等式a=elna和a=lnea可以产生如下常见的五个变形.

一、五个常见变形

例1 (2021年湖北宜昌市联考)若不等式x-4ex-alnx≥x+1对任意x∈(1,+∞)恒成立，求实数a的取值范围.

利用恒等式a=elna和a=lnea，可以用同构法解决如下三种题型的导数题.

二、几种常见题型

题型1积型

三个常见的能化成积型的变形：

(1)λxeλx≥xlnx⟺λxeλx≥(lnx)·elnx→构造f(x)=xex或f(x)=xlnx；

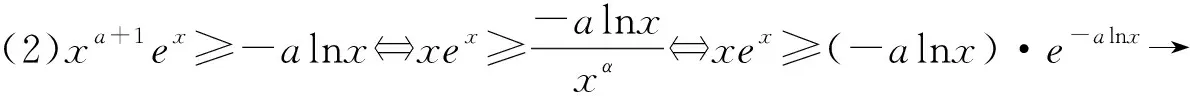
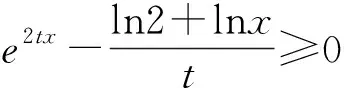
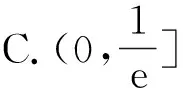
题型2商型

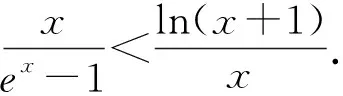
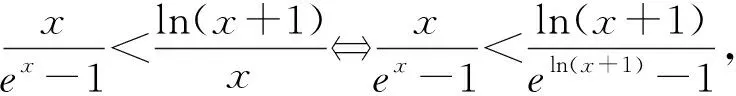
题型3和差型

1.两个常见的能化成和差型的变形.

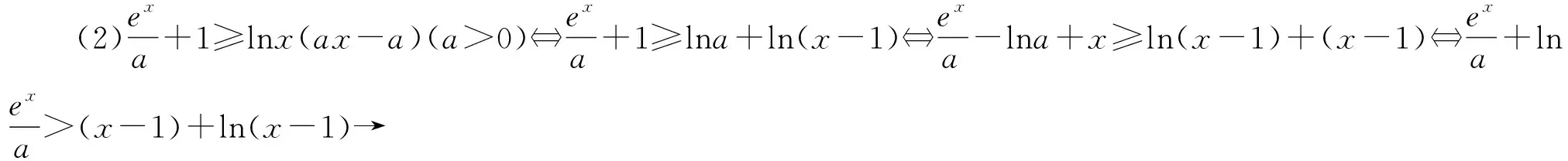
例4 (2019年武汉市江岸区模拟题)已知函数f(x)=ex-aln(ax-a)+a(a>0),若关于x的不等式f(x)>0恒成立，则实数a的取值范围为( ).

A.(0,e2] B.(0,e2) C.[1,e2] D.(1,e2)

2.积型转化成和差型，商型转化成和差型

积型aea

三、高考中的应用

例5 (2020年新高考山东)已知函数f(x)=aex-1-lnx+lna.

(1)当a=e时，求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积；

(2)若f(x)≥1，求a的取值范围.

解：(1)略；(2)f(x)≥1⟺elna+x-1-lnx+lna≥1⟺elna+x-1+lna+x-1≥lnx+x=elnx+x.令g(x)=ex+x，则g(x)是增函数.上述不等式等价于g(lna+x-1)≥g(lnx)⟺lna+x-1≥lnx，即lna≥lnx-x+1，令h(x)=lnx-x+1，求导易得h(x)max=h(1)=0，∴lna≥0，即a的取值范围为[1,+∞).

同构法是一个非常重要的数学解题方法，两个恒等式a=elna和a=lnea是非常重要的工具.在同构法解导数题时，变形能力非常重要，尤其是同构意识，变形能力，缺省补项时，有时出现的比较灵活.平时学习时需要多练习和总结，才能更好灵活应用.