液压悬置系统的幅频特性分析及优化设计
2021-09-06胡金芳张博阳徐有忠李宗保
胡金芳, 张博阳, 徐有忠, 李宗保, 杨 晋
(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009; 2.安徽省汽车NVH 与可靠性重点实验室,安徽 芜湖 241000)
液压悬置作为连接动力总成和车身的主要隔振元件,应满足双向减振的要求[1],即不仅能够减小动力总成传递到车身上的力,同时还能衰减来自路面的激励。目前,很多学者对液压悬置隔振性能的研究主要集中于其频变特性[2]。文献[3]和文献[4]分别采用不同的方法对液压悬置进行了动、静态测试,并分析了液压悬置在不同情况下动刚度和滞后角的频变特性;文献[5]在试验的基础上获得了液压悬置的相应参数,并对液压悬置动特性进行动力学仿真,其结果虽然与试验结果变化趋势吻合,但通过分析文中动刚度和滞后角的对比图可知,液压悬置的频变模型并不能完整地表征其动特性。事实上,液压悬置的动刚度也受激励振幅的影响[6-7],随着激励振幅的不同,橡胶主簧刚度、上液室刚度和惯性通道内液阻等参数都会随激励振幅发生不同程度的变化[8]。因此,在对液压悬置的动特性和动力总成液压悬置系统的隔振特性研究时,有必要对液压悬置的幅变和频变特性进行综合考虑。
本文针对液压悬置频变模型的不足,以惯性通道式液压悬置为例,通过对上液室刚度和惯性通道内的液阻进行参数识别,建立了液压悬置幅频特性模型,并对特定工况下的动力总成液压悬置系统的隔振性能进行优化设计,从而有效改善液压悬置元件的隔振性能。
1 液压悬置幅频特性模型的建立
1.1 液压悬置集总参数模型
液压悬置的集总参数模型如图1所示。图1中:橡胶主簧的刚度和阻尼分别为Kr、Br;惯性通道和解耦盘的流量分别为Qi(t)、Qd(t);惯性通道和解耦盘的流体惯量分别为Ii、Id;液阻为Ri、Rd;上、下液室的体积柔度分别为C1、C2;上、下液室对应的压强为P1(t)、P2(t);Ap为上液室的等效面积。

图1 液压悬置的集总参数模型
根据流体动力学原理,液体的连续方程和流体动量方程[3]为:
(1)
假设连接动力总成的液压悬置上端的激励位移为X(t),则连接螺栓所受的动载荷F(t)为:
(2)
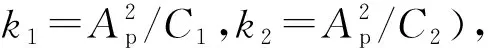
(3)
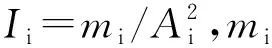

K′(w)+iK″(w)
(4)
取K′、K″分别为存储刚度和损失刚度,则动刚度和滞后角分别为:

(5)
(3)式所建立的液压悬置动刚度模型仅考虑了液压悬置的频变特性,但在液压悬置中,上液室刚度和惯性通道内液阻具有明显的幅变特性[6]。因此,为了准确地表征液压悬置的幅频特性,定义上液室刚度和惯性通道内液阻为:
k1(x)=a(x),Ri(x)=b(x)
(6)
其中,x为激励位移。a(x)和b(x)可以通过对上液室刚度和液阻的识别参数拟合得出,(3)式可修正为具有幅频特性的非线性集总参数模型,即
Kr+Brs
(7)
1.2 上液室刚度和惯性通道内液阻的参数识别
取橡胶主簧刚度为200 N/mm,橡胶主簧阻尼为100 N·s/m,等效活塞面积为3×103mm2,流体质量惯量系数为2.34×106kg/m4。以(7)式计算的动刚度仿真结果与试验曲线[8]之间的误差最小化为目标函数,对不同幅值下的上液室刚度和液阻进行参数识别,结果见表1所列。
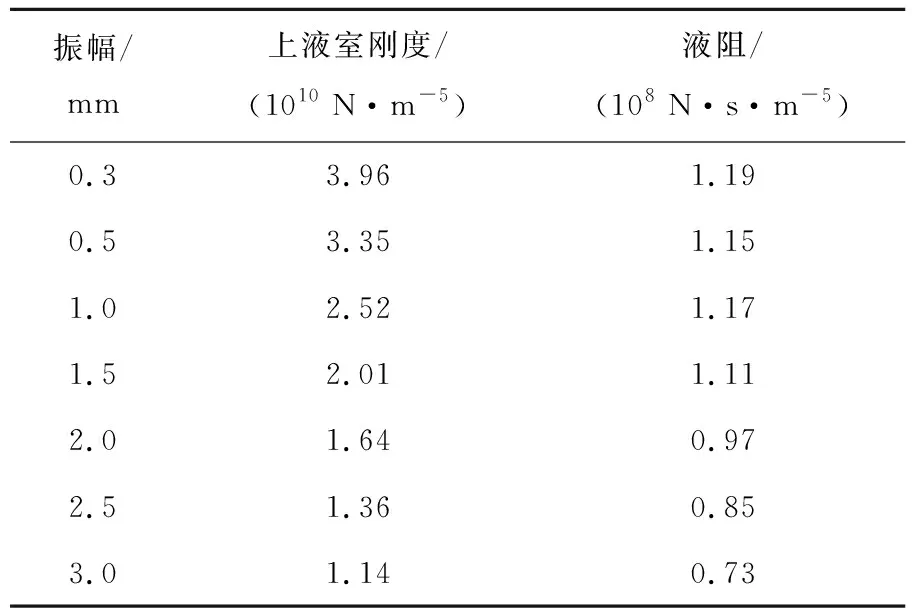
表1 不同幅值下上液室刚度和液阻的识别结果
分别对上液室刚度和液阻的识别结果进行三次多项式拟合,结果如图2所示。由图2可知,拟合相关系数分别为0.999 22、0.993 06,效果良好。

图2 上液室刚度和液阻的辨识结果与拟合结果
由(7)式得到液压悬置动刚度和滞后角的仿真与试验结果对比,如图3所示。
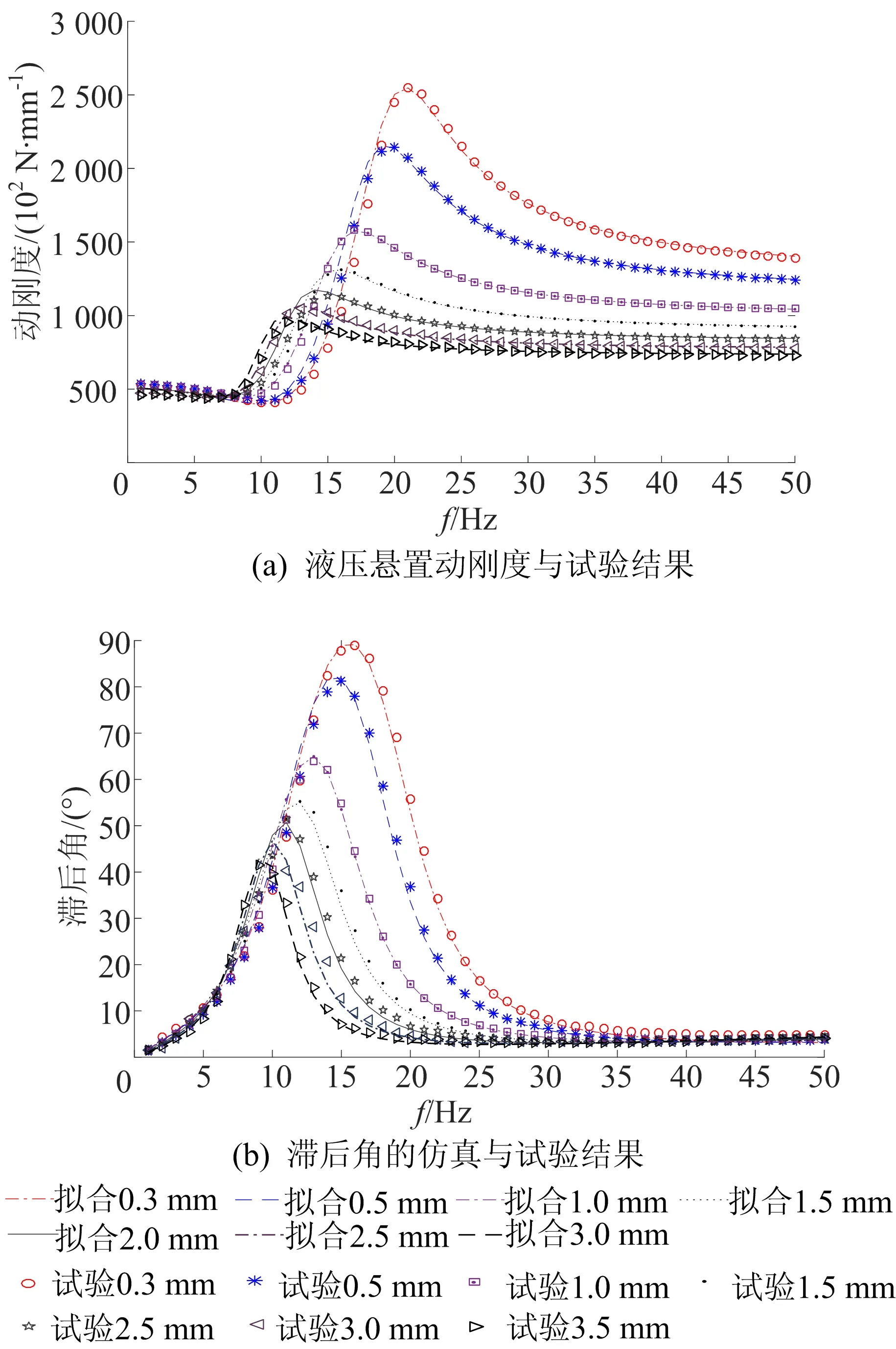
图3 液压悬置动刚度和滞后角的仿真与试验结果对比
由图3可知,两者的吻合程度非常高,验证了液压悬置幅频特性模型的准确性。
2 二自由度整车模型
由于液压悬置主要作用方向是垂直方向,为了充分研究动力总成液压悬置系统的隔振特性,忽略其他方向振动的影响,以液压悬置的幅频非线性特性为基础,构建整车二自由度模型,如图4所示。
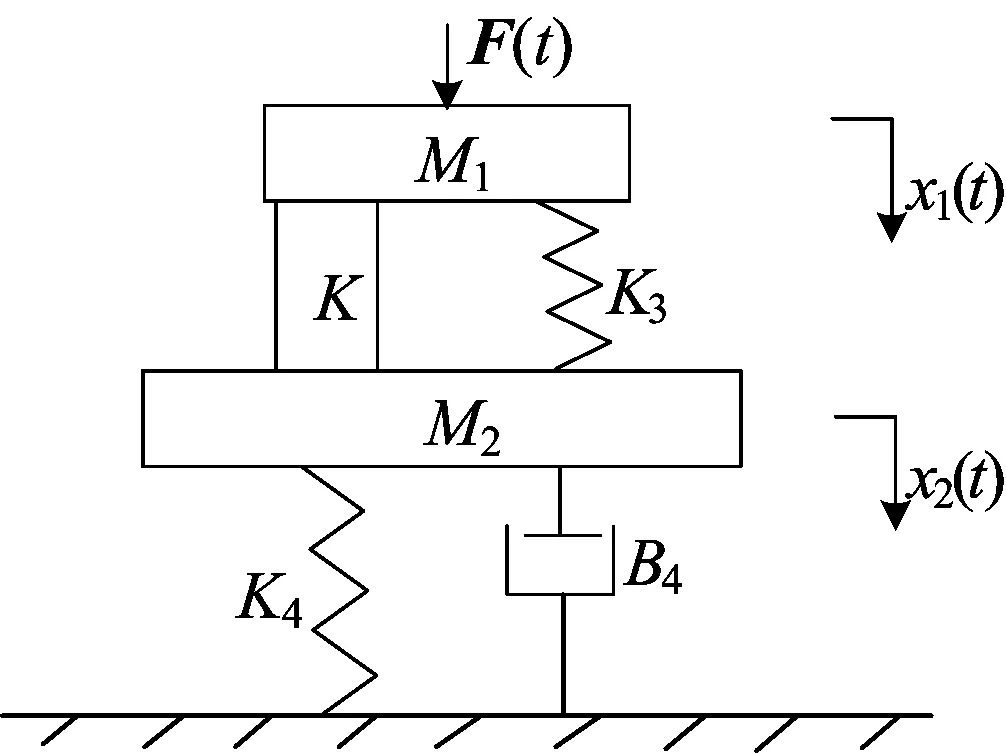
图4 整车二自由度模型
图4中:M1为动力总成部分质量;M2为底盘及车身部分质量。整车的轮胎部分可等效为刚度为K4、阻尼为B4的阻尼器。发动机和车身通过悬置连接在模型中,该悬置由橡胶悬置和液压悬置构成。其中:橡胶悬置的线性刚度为K3;液压悬置的动刚度为K。忽略橡胶悬置的阻尼,运动方程可以表示为:
(8)
对(8)式进行拉氏变换,则车身振动的幅频特性函数G1(s)和车身振动的加速度特性函数G2(s)分别为:
(9)
其中
(M1s2+K+K3)+(K+K3)s2。
3 液压悬置参数优化设计
3.1 优化目标和变量的选取
根据上述分析可知,液压悬置的动刚度由于受激励幅值和频率的影响,表现出很强的动态非线性特性,若仅对液压悬置内部参数进行整体优化,则使动力总成液压悬置系统在整个激励过程中都表现出最优的隔振性能是非常困难的[6]。因此,本文只考虑典型工况下对液压悬置系统进行确定性优化,优化目标[9]设置如下:
(1) 在发动机怠速(780 r/min)时,动力总成的垂向模态一般为12 Hz,为了最大程度地抑制动力总成的垂向振动,将最大动刚度设置在此频率点,定义为f1。
(2) 考虑到路面激励频率一般为9 Hz,将液压悬置最大滞后角所在的频率设置在此频率点f2,这样不仅有利于隔离路面的激励,也可以有效衰减因发动机启动而产生的大幅振动。
(3) 设液压悬置动刚度峰值和滞后角峰值分别在Kdmax=750 N/mm和φmax=70°附近时液压悬置的动特性最佳。
此外,为了更好地隔离发动机的激励向车身的传递,在1~50 Hz的频率段下,将车身振动传递系数c1和车身加速度传递系数c2作为优化的另外2个子目标,即
(10)
其中:j=1,2;sj=i2πfj。使用加权法将6个子目标的多目标优化问题转换为单目标优化问题,对应函数为:
(11)
其中:hi(i=1,…,6)为权重,由于优化中各个目标同等重要,取hi=1;li为比例因子,根据各优化变量的比例大小,分别取l1=l2=l5=l6=1,l3=2 500,l4=25;x=(f1,f2,Kdmax,φmax,c1,c2)。假设怠速情况下动力总成的激励幅值为1.0 mm,选取液压悬置模型中的橡胶主簧刚度Kr、惯性通道长度L、惯性通道截面积a以及橡胶悬置K3、车身振动传递系数c1、车身加速度传递系数c2作为优化变量,其他参数均设为定值。约束条件为:
minF(x),
0.5×180 000≤Kr≤1.5×180 000,
0.5×5×10-5≤a≤1.5×5×10-5,
0.5×0.2≤l≤1.5×0.2,
600≤Kdmax≤1 000,
300 000≤K3≤510 000,
250≤Kd(40)≤650,
65≤φmax≤85,
φmin≥0
(12)
其中:Kd(40)为频率40 Hz时的动刚度值;φmin为滞后角的最小值[9]。
3.2 优化前后结果对比
液压悬置系统确定性优化结果见表2所列。
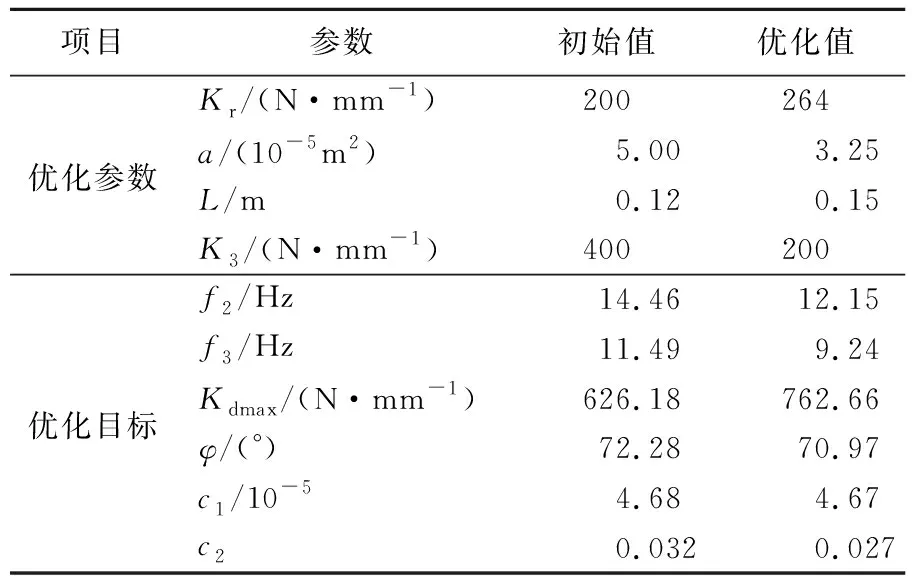
表2 参数优化结果(振幅1.0 mm)
优化前、后液压悬置动刚度和滞后角的动态特性如图5所示。
由图5可知,优化后的动刚度和滞后角在特定点均达到了目标值的要求,且未超出约束边界限制。

图5 动刚度优化和滞后角前后情况对比
优化前、后的车身振动传递率和车身加速度传递率的幅频特性曲线如图6所示。
由图6可知,优化后的振动传递特性和加速度传递特性比优化前有所改善。特别是在9 Hz附近的非簧载质量的共振区间内,车身振动传递率和加速度传递率明显减小,说明优化后的液压悬置有效地抑制了路面激励通过悬架系统向车身的传递,提高了整车的舒适性;同时在25~50 Hz的怠速共振频率以上的频率区间, 优化后的传递率也比优化前小,说明优化后的液压悬置有效减小了动力总成的振动向车身的传递。
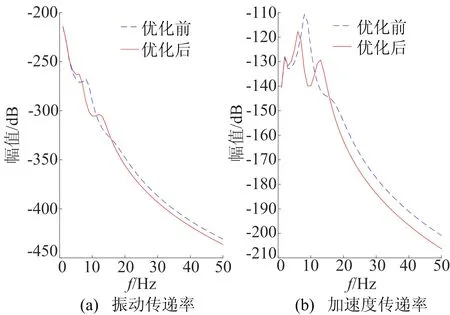
图6 优化前、后车身振动和加速度传递率的辐频曲线
4 结 论
(1) 本文在对液压悬置的上液室刚度和惯性通道内的液阻进行参数识别的基础上建立了液压悬置幅频非线性模型,该模型可以准确地描述其低频段动特性。但需要指出的是,当液压悬置受到高频激励时,解耦盘在解耦通道内会发生小变形以消除动态硬化的现象,此时该模型中的液阻Ri可认为是定值。
(2) 根据建立的整车二自由度模型,采用模式搜索算法对怠速工况下悬置参数进行确定性优化设计。计算结果表明,车身振动和车身加速度传递率明显降低,动力总成液压悬置系统的隔振性能有所提高,证明了本文优化设计方法的有效性。
