基于双重交叉策略的多元宇宙优化算法求解带时间窗车辆路径问题

吴秀芹，刘铁良

（东北石油大学 计算机与信息技术学院，大庆 163318）

带时间窗车辆路径问题（Vehicle Routing Prob⁃lem with Time Windows，VRPTW）［1］是由车辆路径问题（Vehicle Routing Problem，VRP）演化而来的，它是对传统车辆路径问题的进一步扩展［2］。VRPTW一直是组合优化和运筹学领域的热点问题，其在物流配送和车辆路径规划等领域具有十分广泛的应用背景，因此如何有效地解决VRPTW问题具有很高的实际应用和理论研究价值。

随着启发式算法的不断发展，运用群智能优化算法对VRPTW问题进行求解是当前学者们的重要研究方向。刘志伟［3］提出一种结合遗传算法的改进多目标和声搜索算法（GA-MOIHSA）求解多目标VRPTW问题，该算法引入和声模板和多重邻域搜索策略，提高了算法的全局搜索能力。马祥丽等人［4］重新设计了蝙蝠算法（BA）的操作算子，提出一种改进的蝙蝠算法求解VRPTW问题。黄震等人［5］提出一种混合蚁群优化算法求解带时间窗车辆路径问题（VRPTW）。苗国强等人［6］提出一种自适应大规模邻域搜索算法求解VRPTW，该算法引入移除和插入规则，并采用局部搜索策略来提高解的质量。王君［7］设计了一种离散差分进化混合算法求解VRPTW问题，该算法通过构造新的变异算子和交叉算子来提高算法的寻优能力。

多元宇宙优化算法［8］（Multi-Verse Optimizer，MVO）是由澳大利亚学者Mirjalili教授于2016年设计的一种新启发式优化算法。与粒子群算法、蚁群算法等经典的启发式算法相比，MVO算法操作简单且参数设置少，同时有良好的全局搜索能力。目前在国外，许多学者利用MVO算法解决经济调度［9］、工程优化［10］和求解光伏发电机组参数［11］等问题，取得了良好的实际应用效果。但国内对MVO算法在实际工程问题中的研究相对较少。因此，本文提出一种基于双重交叉策略的多元宇宙优化算法（Multi-Verse Optimizer Algorithm Based on Double Crossover Strategy，DCSMVO），并将其应用于求解VRPTW问题。在DCS-MVO算法中，首先在满足车辆最大载重的约束条件下，通过访问概率来构造算法的初始解，提高了初始宇宙群的优良性；其次，引入动态交叉算子，保证迭代后期宇宙种群的多样性，提高算法的局部探索能力；同时采用基于最优片段的交叉策略，加强宇宙间信息的交互，提高算法的全局开发能力；此外，引入随机交换搜索、2-opt和3-opt相结合的邻域搜索策略，以便寻找到更多潜在的优秀解。最后对改进效果进行仿真验证，并将DCS-MVO与其它5种优化算法在求解本文建立的模型上进行对比，DCSMVO取得了很好的寻优效果。

1 数学模型

本文研究的带时间窗车辆路径问题［12］，即有一个配送中心和多个客户需求点，不仅要满足车辆最大载重等约束条件，还需要满足在指定的时间区间内将商品交付到指定客户点，所有配送车辆完成配送任务后必须返回配送中心。求解VRPTW的目标是在满足约束条件的基础上合理安排车辆路线，使配送的总成本最低。

在VRPTW中，N={1 ,…,n}为客户集合，V={0 ,N}为配送中心（定义为0）和所有客户集合，K={1 ,2,…,m} 为配送中心的车辆集合，Vk为车辆k访问客户点的集合，R为车辆最大载重，ri为各客户点的需求量，表示车辆k由客户i行驶到客户 j（=1 为从 i行驶到 j，=0为不行驶），表示客户i由车辆k提供服务（=1为由车辆k提供服务，=1表示未提供服务），dij为客户点i到客户点j的距离，C为每辆车的固定费用，Pi表示时间惩罚成本，STi表示客户i接受配送服务的最早开窗时间，ETi表示客户i接受配送服务的最晚闭窗时间，其中ti是车辆达到客户i的时间，当配送车辆不在规定的时间范围内[STi,ETi]为客户i提供配送服务，将会产生一定的时间惩罚成本，a表示早到惩罚系数，b表示晚到惩罚系数。则VRPTW的数学模型如下：

式（1）为目标函数，F1表示物流总成本（包括车辆固定成本、运输成本以及时间惩罚成本）；式（2）表示每辆车不得超过其最大载重量；式（3）表示车辆从配送中心出发完成配送任务后必须返回配送中心；式（4）表示车辆服务完客户i后再去服务客户j；式（5）表示车辆服务客户j之前服务客户i；式（6）表示每个客户只能被一辆车服务；式（7）表示物流配送中产生的时间惩罚成本；式（8）和式（9）表示决策变量约束条件。

2 基于双重交叉策略的多元宇宙优化算法

2.1 传统多元宇宙优化算法

多元宇宙优化算法（MVO）主要依据于物理学中多元宇宙理论，模拟的是宇宙种群在白洞、黑洞和虫洞相互作用下的运动行为而构建的数学模型。在该数学模型中，每个宇宙被看作优化问题的一个解，宇宙中每个物体代表解的一个分量，宇宙膨胀率则代表目标函数的适应度值。MVO算法在每次迭代时，首先通过轮盘赌原则，根据排序后宇宙种群的膨胀率选择一个白洞，其更新公式如下：

为了保证宇宙种群的多样性，宇宙内物体会不断向当前最优宇宙移动，其更新公式如下：

其中，xj表示目前形成的最佳宇宙中的第j个分量；lbj为第j个分量的下界；ubj为第j个分量的上界；为第i个宇宙的第j个分量；r2,r3,r4是在[0,1]之间的随机数；WEP表示宇宙中虫洞存在概率；TDR为旅行距离率。其更新公式如下：

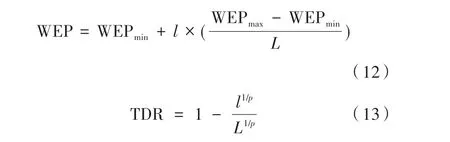
其中，WEPmin为WEP的最小值（取值为0.2），WEPmax为WEP的最大值（取值为1）；l为当前迭代次数；L为最大迭代次数；p为开发的准确性（取值为6）。

2.2 基于双重交叉策略的多元宇宙优化算法设计

2.2.1 优化个体的编码与解码

多元宇宙优化算法求解VRPTW问题时，每个宇宙表示一条配送路径，宇宙的每个分量表示配送路径中的客户点。由于客户点的编号方式是整数类型，为了使宇宙中个体的位置按照客户编号规则与VRPTW问题形成一一对应的关系，因此选择自然数的编码方式。用一维向量表示一条配送路径，一维向量中的每个字符代表每一个客户，向量的长度表示客户总数。具体的编码方式如下：

假设客户数为n，车辆数为m，根据VRPTW模型的特点：“0”认为是配送中心，因此需要在客户点集合的位置前后分别加上“0”，构成一条完整的VRPTW路径，即配送车辆从配送中心出发完成配送任务后需返回配送中心，配送车辆达到客户点的顺序构成一台车辆的访问路径。例如：n=9，m=3，由于3辆车配送的客户点集合分别为{1 ,6,4,5} ，{9,7,3}，{2,8}。因此，3辆车的访问路径分别为：{0 ,1,6,4,5,0} ，{0,9,7,3,0}，{0,2,8,0}。

2.2.2 初始解构造

初始宇宙个体对路径节点的合理选择，可以提高宇宙群的整体质量。本文采用根据客户点的访问概率来构造问题的初始解，允许对客户点的配送服务时间不在期望的时间窗内，但必须满足车辆最大载重限制，设配送车辆规格相同，车辆的最大载重量为R，dij为客户i与客户j之间的距离，K为配送中心所包含的车辆总数，初始解的构造步骤为：

（1）初始化k=1，且配送中心“0”为配送起点。假设车辆k已经配送的客户节点集合为Vk，待配送的客户节点集合为Nk，在集合Nk中随机选取一点作为访问路径的起点。

（3）若客户i的商品需求量为ri，Rk为车辆k的剩余载重量，则 Rk=Rk-ri，若Rk>0，则 Vk=Vk⋃{i}，将客户节点i加入已配送客户集合中，转步骤（2）；若Rk<0，则超出最大车辆k的最大载重约束，转步骤（4）。

（4）添加一个新的配送车辆，k=k+1，且k≤K，重复步骤（1）-（4），直到集合 Nk中没有待配送的客户点。

2.2.3 改进方法

（1）基于动态交叉算子的交叉策略

传统多元宇宙优化算法中，黑洞通过虫洞在最优宇宙周围以旅行距离率（TDR）进行局部探索，随着迭代次数的增加，TDR值逐渐减小，导致迭代后期的旅行距离率较小，算法的局部探索性能大大降低，易造成宇宙种群多样性的减少，导致算法过早陷入局部最优。为了提高MVO算法的局部寻优性能，本文引入差分进化算法［13］中的交叉算子，通过交叉操作来提高宇宙种群的多样性，避免算法过早停滞。

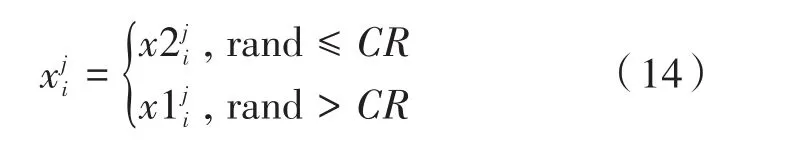
其中，CR是交叉算子，也称交叉常量，通常取[0,1]范围间的常数。CR取值越大，中分量被选中的概率越大，越接近，反 之越接近。通过阅读文献可知，CR较好的取值范围在0.3到0.9之间。根据VRPTW模型的特点，本文动态选取0.3到0.9之间的值作为交叉常量，随机选取和中的分量重组成新的宇宙。通过上述交叉策略，丰富了宇宙种群的多样性，避免算法过早陷入局部最优，提高算法的局部探索能力。基于动态交叉算子的更新策略如图1所示。

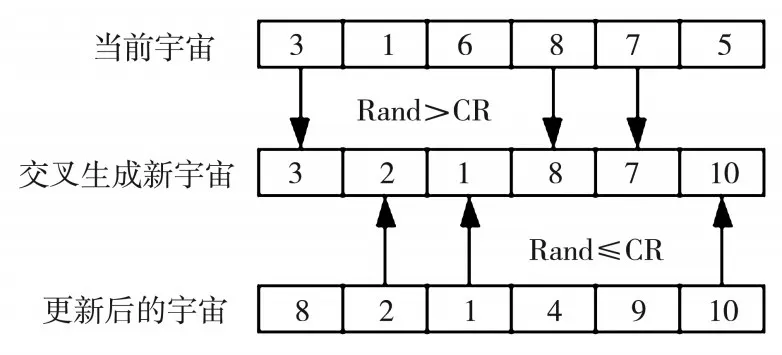
图1 基于动态交叉算子的更新策略图

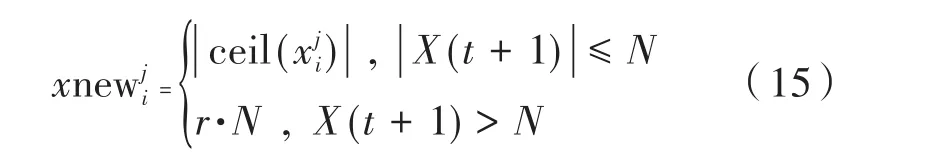
（2）基于最优片段的交叉策略

传统MVO算法中，通过轮盘赌原则选择出的白洞基本上就是最优宇宙，由于没有很好与其它宇宙进行充分的信息交互，这使得算法缺乏跳出局部最优的能力，也容易导致宇宙种群早熟，进而无法进行深度的全局开发。为了提高算法的全局开发能力，本文采用基于最优片段的交叉策略来更新白洞的位置。假设最优宇宙为，当前宇宙为，随机截取最优宇宙中的部分片段，将其插入到当前宇宙为的尾部，同时将宇宙中重复的分量删除，得到基于最优片段的新路径方案。基于最优片段的交叉策略方法如图2所示。

图2 基于最优片段的交叉策略图

如图2所示，宇宙中的每个分量表示VRPTW问题中的每个客户点，每个宇宙表示一条配送路径，通过在最优配送路径中随机截取部分片段，如截取客户9到客户2之间的配送路径，将其插入到原配送路径的尾部，同时将原路径中重复的客户删去，得到一条新的配送路径。

2.2.4 邻域搜索策略

根据VRPTW的特点，借鉴文献［14-16］的邻域搜索策略，本文提出了随机交换，2-opt，3-opt相结合的局部搜索策略。

（1）交换搜索：对配送路径进行交换搜索，随机选取两个不同位置的客户点，将两个客户点位置交换。更新方式如图3所示。

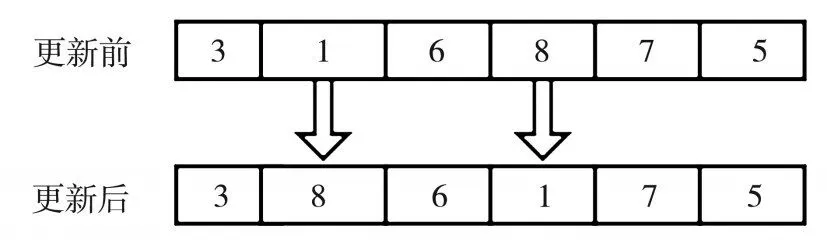
图3 交换搜索略图

（2）2-opt搜索：对配送路径进行2-opt搜索，随机选取两个不同位置的客户点，将两个客户点之间的位置全部反转。更新方式如图4所示。

图4 2-opt策略图

（3）3-opt搜索：对于配送路径进行3-opt搜索，随机选取3个位置的客户点依次交换。更新方式如图5所示。

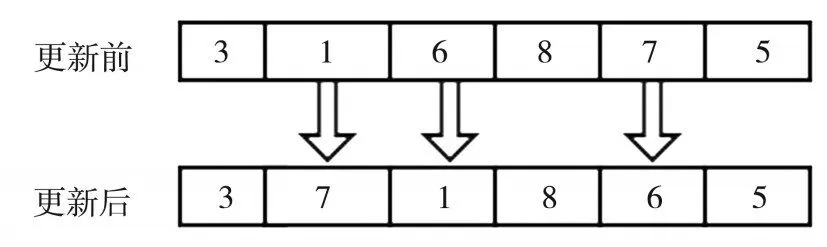
图5 3-opt策略图

选择上述的邻域搜索策略对每次迭代得到的最优解进行变换，产生更多的邻域解，选择适应度最小的值作为每代的最优解，本算法的局部搜索策略按照一定的规则来交换客户的访问次序，得到的路径仍然对应着一个完整的VRPTW路径。

2.3 算法的基本流程

基于双重交叉策略的多元宇宙优化算法的具体步骤如图6所示。

图6 DCS-MVO算法流程图

3 实验与分析

本文采用Solomon的6种类型VRPTW算例［13］测试DCS-MVO，然后将DCS-MVO和传统多元宇宙优化算法（Multi-verse Optimization，MVO）、飞蛾扑火算法（Moth Flame Optimization，MFO）、布谷鸟算法（Cuckoo Search Algorithm，CSA）、粒子群算法（Particle Swarm Optimization，PSO）和蝙蝠算法（Bat Algorithm，BA）进行比较实验。DCS-MVO的参数设置如下：MaxIt=1000，popnum=100。MVO、MFO、CSA、PSO和BA的基本参数设置同DCS-MVO一致。表1给出部分算例实验结果，以总成本（车辆固定成本、运输成本和时间惩罚成本之和）最小为优化目标，求解最优的路径配送方案。因此求解总成本的值越小，则表明算法在求解VRPTW问题上的性能越好。

通过表1分析可知，DCS-MVO算法求解C型测试集时，由于C型测试集的客户位置主要成聚类分布，随机生成的初始种群具有一定的混乱性，容易破坏其原有的路径结构，造成大量的冗余路径，而DCS-MVO算法利用访问概率构造初始种群，相对弱化了VRPTW模型的约束条件。因此DCS-MVO求解得到的总成本要低于其它五种优化算法，相比较传统MVO算法，DCS-MVO算法对C型问题的求解结果有所改进。对于R1型和RC1型测试集，由于客户点分布较为均匀，并且每个客户要求的配送时间范围比较紧凑，在路径配送方案规划中，可能会产生更多的车辆固定费用和时间窗惩罚费用，因此DCS-MVO算法优化得到的总成本略优于其它五种算法；对于R2型和RC2型测试集，客户的时间窗范围较大，对配送时间的要求比较宽松，因此相较于其他算法，DCS-MVO算法得到的优化效果更好。

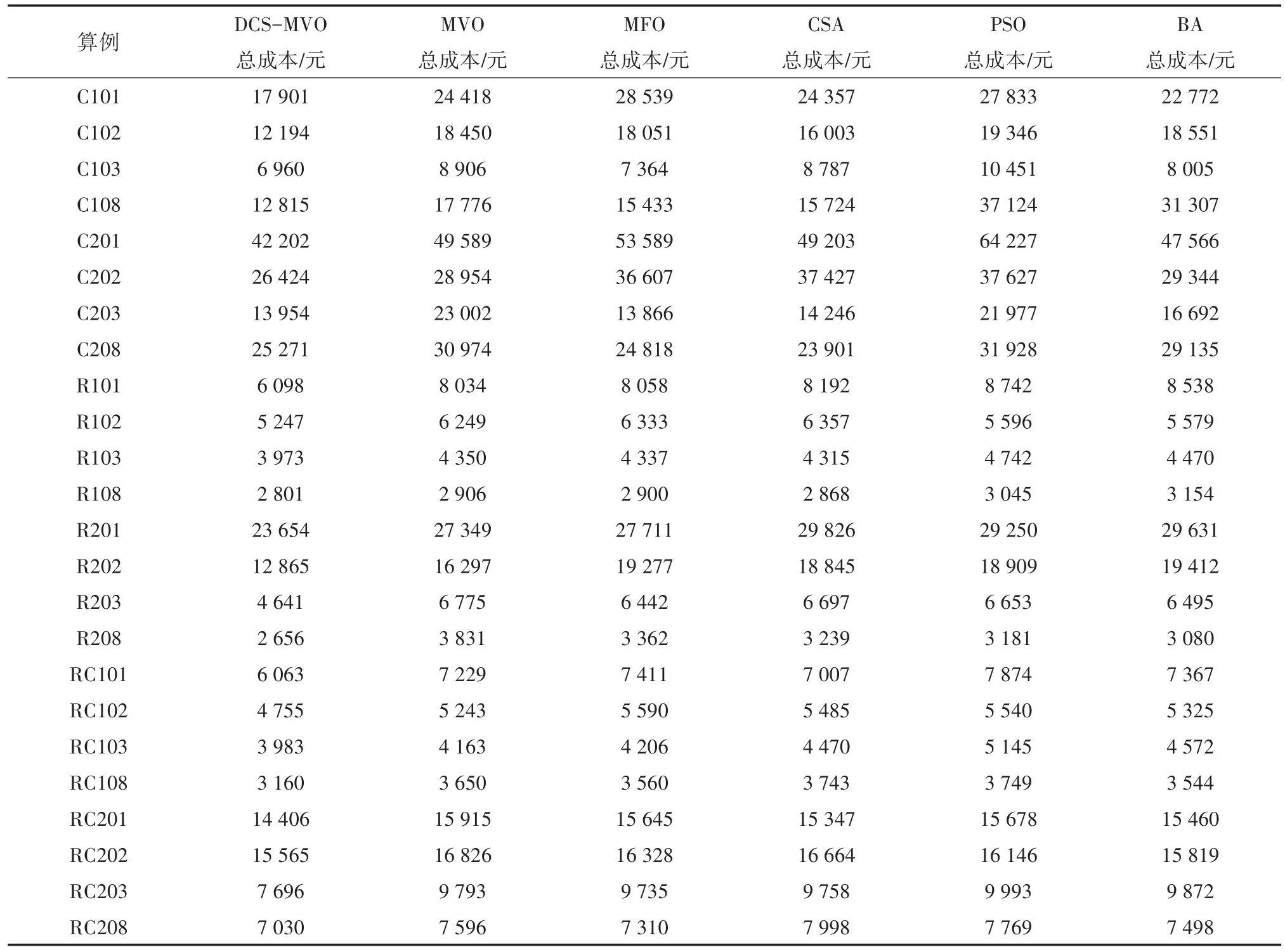
表1 部分算例实验结果对比

为了具体验证DCS-MVO算法在求解VRPTW问题的性能，本文分别用DCS-MVO、MVO、MFO、CSA、PSO和BA算法对VRPTW的数学模型进行求解。在Solomon数据集中以C101、C201、RC208三种算例做具体分析，其结果如下所示：

其中，C101算例求解得到的运输成本为832.170 1元，所需车辆为10辆，总成本为17 901元，与目前最优运输成本828.94元接近，从而证明DCS-MVO算法在求解C101上有较好的寻优能力；C201算例得到的运输成本为589.76元，所需车辆为3，总成本为42 202元，与目前最优运输成本591.56元接近，因此，DCS-MVO算法在求解C201上有良好的寻优效果；RC208得到的最优运输成本为817.878 9元，所需车辆为3，总成本为7 030元，优于目前最优运输成本828.94元，证明DCS-MVO算法在求解RC208上有很好的寻优能力。

图7、8、9表示C101、C201和RC208的最优配送路线图，图10、11、12为六种算法在求解C101、C201、RC208算例时的总成本迭代图，其中，横坐标表示算法的迭代次数，纵坐标表示总成本（包括车辆固定成本、运输成本和时间惩罚成本），通过上图反映了DCS-MVO算法有较好的求解能力。在算法迭代初期，DCS-MVO算法通过访问概率构造VRPTW模型的初始解，加快了算法的收敛速度；随着迭代次数的增加，DCS-MVO算法采用双重交叉变异策略，丰富了宇宙种群的多样性，使算法能够充分挖掘搜索空间，有效提高算法跳出局部最优的能力；此外，DCS-MVO利用交换搜索、2-opt搜索和3-opt搜索相结合的邻域搜索策略对最优解进行变异，可以找到更多的潜在优秀解。因此相较于其它五种算法，DCS-MVO算法求解得到总成本更低。验证了DCS-MVO算法在求解VRPTW问题时，具有较好的寻优能力，可以得到高质量的结果。

图7 C101最优路径图

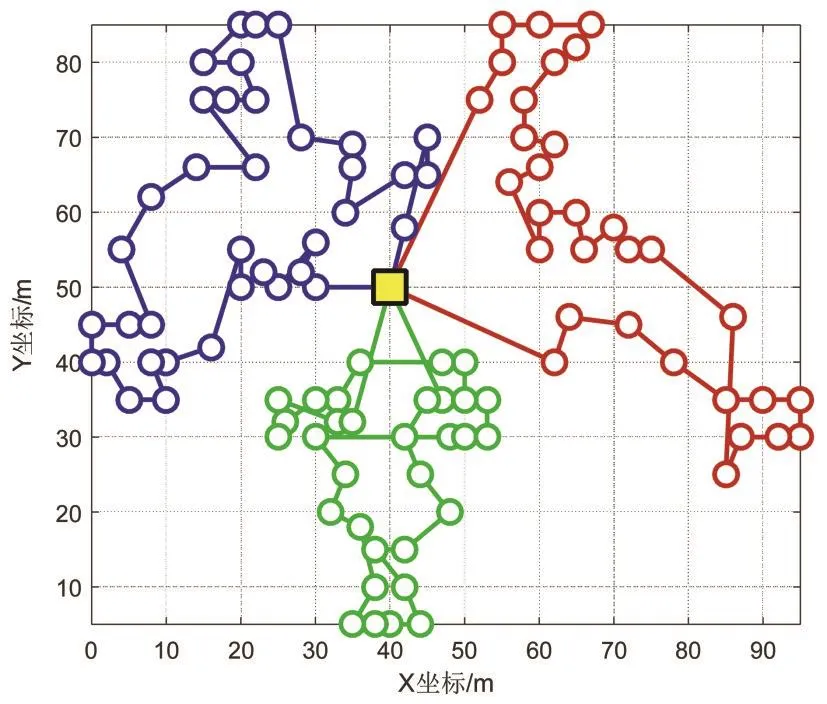
图8 C201最优路径图

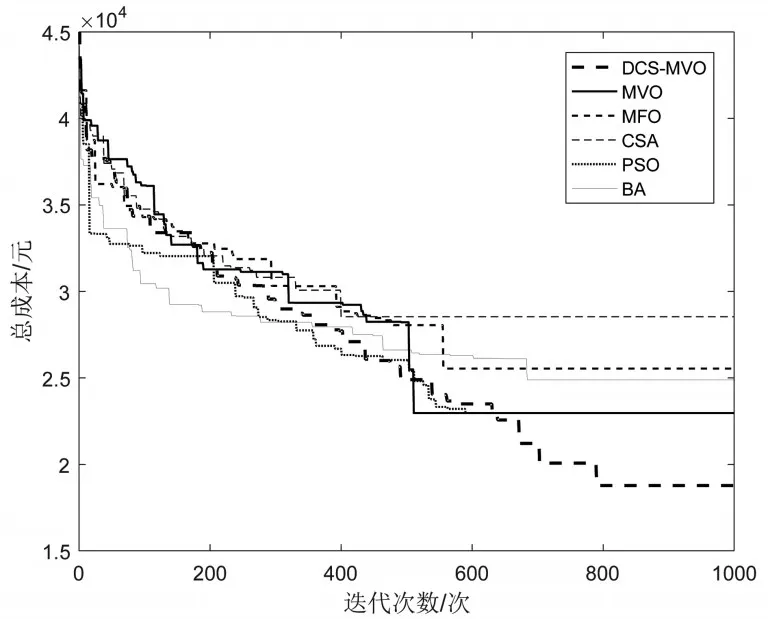
图10 C101总成本迭代图

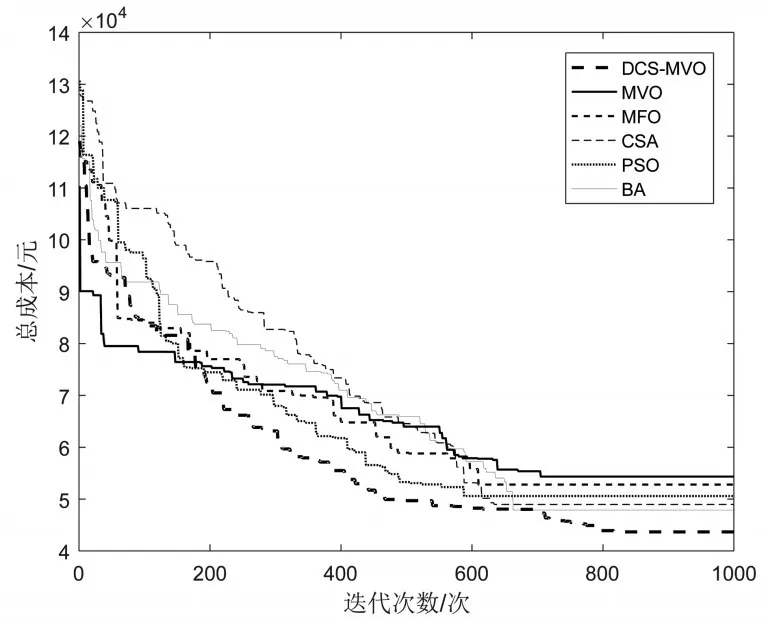
图11 C201总成本迭代图

4 结论

针对VRPTW的求解，本文提出了一种基于双重交叉策略的多元宇宙优化算法。该算法利用访问概率来构造问题的初始解；采用两种交叉策略对宇宙位置的更新策略进行改进，使其更符合求解VRPTW问题的需求；并引入随机交换搜索、2-opt、3-opt策略对最优路径进行邻域变换，增强算法局部搜索能力。算例验证及分析表明，DCS-MVO能够有效求解VRPTW，寻优质量优于所对比算法。未来将进一步改进DCSMVO，以加强其在车辆路径规划问题上的应用。