光学测量平台航空运输性能仿真与试验验证

徐志文，张晗，王强龙，2，刘震宇，王晓明

（1.中国科学院 长春光学精密机械与物理研究所，长春 130033；2.中国科学院大学，北京 100039）

对于光学测量平台等精密仪器，其在运输过程中的稳定性和安全性是十分值得关注的问题［1-3］。在地面运输过程中，会经历连续力学载荷，载荷的特点一般是以随机振动为主（频率范围约为 5～ 200 Hz），兼有周期性载荷［4］。而在航空运输中，载荷更加复杂和严峻：在飞机起飞、降落、跑道滑行等过程中会受到冲击载荷作用，在过程中会受到宽带随机振动、窄带随机振动和正弦振动等几种载荷作用［5］。

如果在运输过程中没有对设备进行隔振等保护，可能对设备结构造成一定损伤，使得设备后续使用安全性存在隐患［6-7］。对于光学测量平台这类精密仪器，会在振动过程中出现关键设备或零部件松动，丢失精度等情况，导致设备无法正常工作［8］。

为保证设备能承受运输过程中的振动环境，在使用前，必须对其进行各种振动环境的模拟考核试验（简称振动试验）［9］。本文参考喷气式运输机的宽带随机振动功率谱对光学测量平台进行随机振动试验，验证设备在航空运输载荷作用下的振动性能。并且在随机振动试验之前，先通过有限元模拟的方法计算设备对振动载荷的响应，保证其在振动台试验时不会损坏。

1 模态分析

1.1 有限元模型

光学测量平台主体采用大理石装配而成，大理石作为一种优质的抗振材料，近年来被广泛应用于各类精密平台。其材料阻尼因子相较一般的金属高，可将结构的振动快速衰减。

对光学测量平台的几何模型进行网格划分，平台上安装的镜筒及各类组件等由于对结构整体的刚度影响不大，所以简化为质量点，使用刚性单元固定在结构表面，最终的有限元模型如图1所示。

图1 光学测量平台有限元模型

在模型中，规定竖直向上为Z轴方向，沿底部凹槽长度方向为X轴方向，Y轴按照右手定则确定。

1.2 无工装模态敲击试验及模态修正

为了使建立的有限元模型更加符合实际状态，根据模型修正理论，先进行模态试验，再通过试验的结果对建立的有限元模型参数进行修改，使模型的动力学特性和实际保持一致［10-11］。对正常工作状态（无隔振工装）下的设备进行模态敲击试验，通过敲击得到的频域响应曲线峰值判断出结构的模态频率。再对有限元模型进行模态分析，通过调整大理石的材料属性将模态频率向试验模态结果靠近，最终大理石的材料属性如表1所示。

表1 光学测量平台大理石的材料属性

最终的模态分析结果如表2所示，表中给出了结构前4阶模态的频率、振型描述以及与敲击试验的对比结果，对应的模态振型图如图2所示。

表2 无隔振工装前4阶模态及振型描述

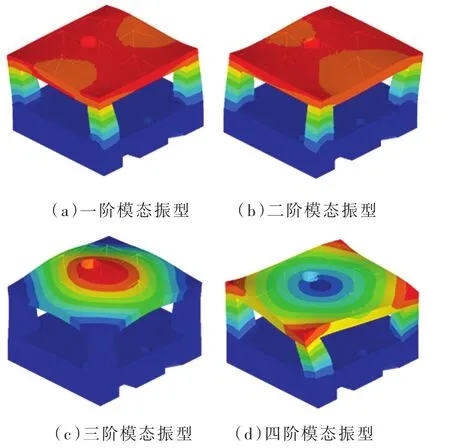
图2 模态振型图

模态分析和模态试验结果的模态频率误差最大为8.8%，可以认为有限元模型与实际结构的动力学特性基本保持一致，后续可以使用该有限元模型进行动力学分析。从模态振型图可以看出，第3阶模态为上平台Z向振动模态，由于上平台表面安装了大量的光学零部件，不方便敲击，所以在敲击试验中未能体现出此阶模态。

1.3 隔振工装下的模态分析

在前一节的基础上，分析设备在隔振工装下的模态，得到前4阶模态如表3所示。由于隔振工装的刚度较小，整体的一阶模态频率有明显下降。

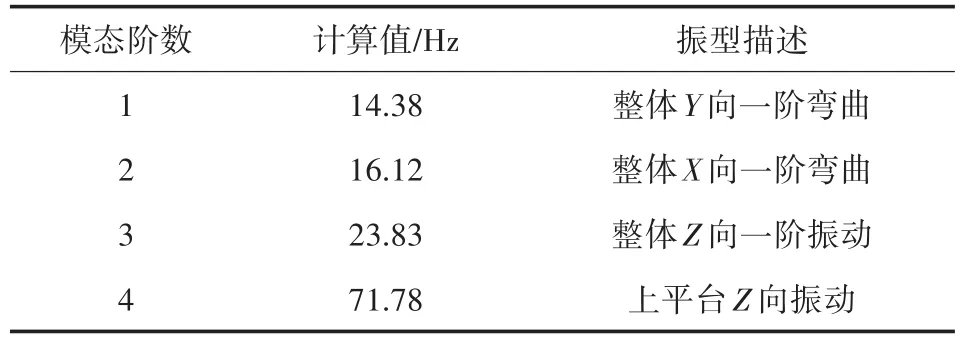
表3 有隔振工装前4阶模态及振型描述

2 动力学响应分析

为了检验光学测量设备的动力学特性，为后续的振动台试验做准备，需要对其进行有限元动力学分析。在设备上选取3个关键部位作为评价点，如表4所示。

表4 光学测量平台动力学分析的评价点

2.1 频率响应分析

频率响应分析是在一定的频域范围内对有限元模型施加一定的激励，包括位移、速度、加速度和力激励等，可以计算出设备在该激励下某些评价点的响应，由此判断出设备在该频域段内的动力学特性，是较为常见的动力学响应分析。

基于上一节建立的有限元模型，分别施加3个方向的频率范围在0～ 500 Hz的单位加速度激励，计算设备在安装隔振工装的条件下，各个方向对加速度激励载荷的放大。得出的频率响应曲线如图3-图5所示。

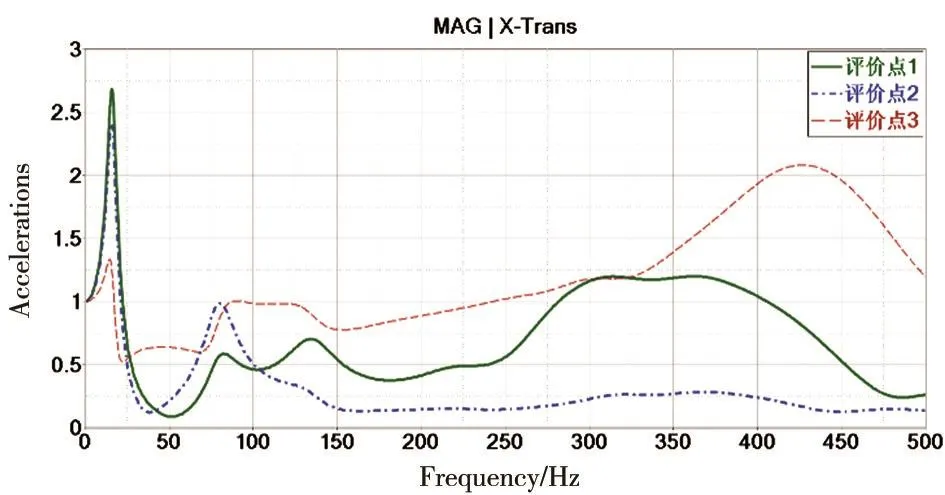
图3 X方向激励时，评价点在X方向的加速度响应曲线

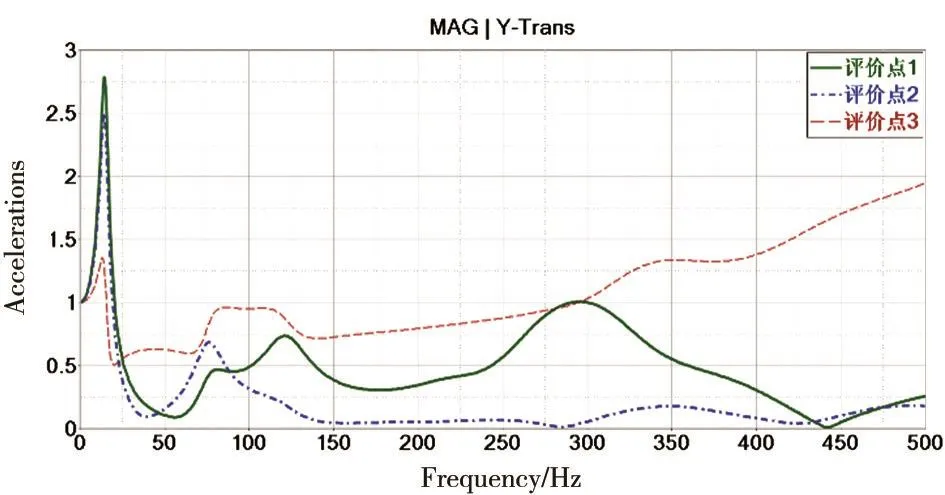
图4 Y方向激励时，评价点在Y方向的加速度响应曲线

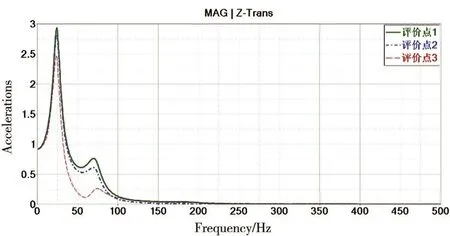
图5 Z方向激励时，评价点在Z方向的加速度响应曲线

图3-图5分别是三个评价点在X/Y/Z方向单位加速度载荷激励下，对应方向的加速度响应曲线。从曲线中可以看出，无论激励方向如何，在低频段都有明显的峰值。而在隔振设计中，往往是低频的振动难以消除，所以要关注设备在低频段内对加速度激励的放大情况，如表5所示。

表5 各评价点的加速度频域响应峰值及所在频率

在Z方向施加激励时，三个评价点共振频率较为一致，在24 Hz左右，根据模态分析结果，判断为整体Z方向一阶振动模态的共振；从放大倍率来看，三个点在共振点对加速度的放大在2～ 3倍之间，对于一般结构来说属于正常范围；X和Y方向激励时，对应方向峰值放大倍率略小于Z方向，峰值所在频率集中在13～ 16 Hz，从模态结果来说属于整体的一阶弯曲模态。

据此，判断此结构关键部位的三个评价点对加速度的放大都在正常范围内，这也与大理石较高的材料阻尼因子有关。

2.2 随机振动响应分析

为了验证设备在航空运输中的性能，参考喷气式运输机的宽带随机振动量值，给出本次随机振动试验的功率谱曲线，如表6所示。

表6 随机振动试验功率谱

对有限元模型进行随机振动响应分析，将功率谱曲线沿Z方向加载，得到如图6所示的各评价点Z方向的功率谱密度曲线，图中可以看出，响应主要集中在低频段。将均方根值统计，与输入的均方根值做商得到振动加速度的传递率，如表7所示。

图6 各评价点Z方向的功率谱密度曲线

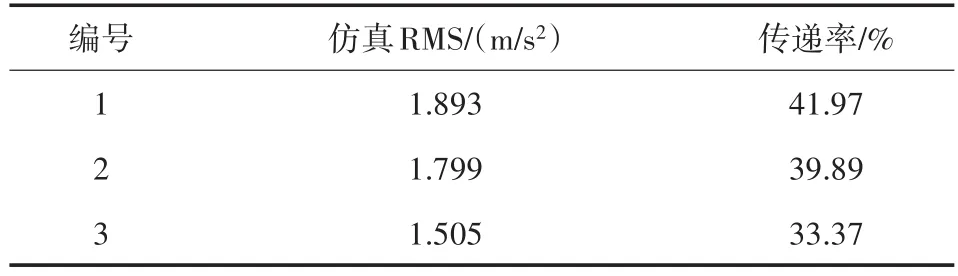
表7 各评价点的响应均方根值及加速度传递率

从表中可以看出，在3个关键部位的评价点加速度传递率都不足50%，均方根值最大为1.893 m/s2，说明工装的隔振效果较好，能有效地将喷气式运输机在飞行过程中产生的宽带随机振动降低，对设备起到了明显的保护作用。

3 振动台试验

在实际测试过程中，大理石平台底面四角通过螺栓与隔振工装连接，隔振工装再通过螺栓和压板与振动台连接。在与动力学仿真中3个评价点相同的位置粘贴加速度传感器，采集振动试验过程中关键部位的加速度响应。试验现场情况如图7所示。

图7 振动台试验现场照片

3.1 正弦扫频试验

在随机振动试验开始之前，先进行一次正弦扫频试验，输入条件如表8所示。

表8 正弦扫频试验输入条件

正弦扫频试验约进行85 s，在3个评价点位置测得的Z向加速度时域信号如图8所示，图8中可明显看出，结构在26 s左右出现明显峰值，说明此时达到结构的共振频率范围。

图8 正弦扫频试验3评价点的加速度时域信号

对23～ 29 s范围内的信号进行快速傅里叶变换获得其频谱，如图9所示。可以看出，3处评价点的最大响应均出现在24 Hz，与仿真结果一致，为结构整体的Z向振动模态。

图9 正弦扫频试验3评价点时域信号的FFT

将振动试验幅值与振动台激励相除得到加速度响应的放大倍率，结果如表9所示。从表9中结果看出，试验和仿真结果相差最大为13%，较为接近，误差存在的原因主要是有限元模型未能对隔振工装的阻尼特性进行准确地描述。

表9 正弦试验与仿真加速度放大倍率结果对比

3.2 随机振动试验

按表6给出的随机振动试验功率谱进行振动台试验，通过之前粘贴的3个加速度传感器采集所在评价点的加速度响应时域信号，使用MATLAB编写程序计算得到相应的PSD曲线，如图10所示。

图10 随机振动试验中各评价点的PSD曲线

图10中可看出，曲线在共振频率点24 Hz左右出现峰值，随后有明显下降；3处评价点响应曲线的特性相似，说明结构整体刚度较好；相比于仿真结果，在高频区存在响应峰，但量级较小可以忽略。对响应时域信号进行计算得到对应评价点的加速度RMS值，如表10所示，与仿真分析结果对比发现，振动台试验的结果明显偏大，两者结果的吻合性不好。

表10 随机振动试验3评价点的加速度响应RMS

经过对振动台输入信号的统计，振动台实际输入的加速度RMS值为6.246 m/s2，要高于设计值的4.51 m/s2，基于此，统计振动台随机试验的加速度传递率并与仿真结果对比，结果如表11所示。

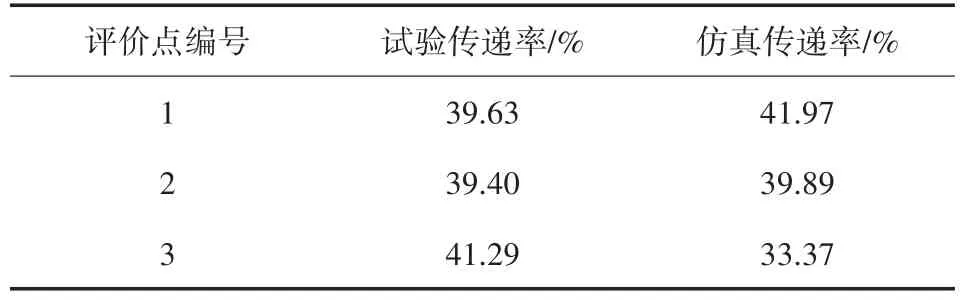
表11 随机振动试验与仿真加速度传递率对比

在表11中可以看出，仿真与试验的结果比较接近，加速度的传递率都保持在了40%左右。

4 结论

为了验证光学测量设备的航空运输性能，本文首先建立了设备的有限元模型，基于模态修正理论，建立了与模态试验结果保持一致的有限元模型。

使用建立的有限元模型进行了频率响应分析，在Z向载荷激励时，结构在24 Hz时出现共振峰，对加速度的放大在2-3倍之间；又进行了随机振动响应分析，在3个关键部位的评价点加速度传递率最大为41.97%，均方根值最大为1.893 m/s2，据此判断设备整体的振动量级较小，对喷气式运输机的宽带随机振动激励有较为明显的衰减。

最后，在振动台上进行了正弦扫频试验和随机振动试验，试验结果和仿真分析结果基本保持一致，再次说明了设备在典型的喷气式运输机宽带随机振动载荷下的航空运输可行性。