一种改进的水下偏振图像融合算法研究
2021-09-04杨威王晓曼赵海丽张谷祥
杨威,王晓曼,赵海丽,张谷祥
(长春理工大学 电子信息工程学院,长春 130022)
我国海域辽阔,海洋中储藏着各种资源,人们的研究重点不断的被吸引到对海洋的探索。传统观念认为,海洋环境相对于陆地环境,较为单一,海洋干扰因素较少,海洋目标更容易被探测识别。但是海洋观测容易受到气候条件影响,有时会造成目标与背景对比度反差较小,此时采用传统的成像技术获得的光强图像,很难将目标区分出来。采用偏振成像技术则可以很好的克服此缺陷,它可以有效地降低海洋环境对被测目标的干扰,如偏振度图像可以提高海洋目标与背景环境的对比度,使被测目标凸显出来[1-2]。
图像融合是指将包含同一场景的不同图像进行综合,使图像能够更好地还原被测目标物信息的过程。自上世纪80年代以来,图像融合技术在各个领域就已经开始有所应用,如偏振遥感图像融合、多模态医学图像融合、海面雾天军事目标识别等。Ruxue Zhao等人提出一种基于边缘信息增强的多尺度强度和偏振差的图像融合算法,将偏振强度图像与局部放电图像融合,该方法能很好的实现浑浊环境下图像的边缘增强;Gemine Vivone等人将低空间分辨率的多光谱图像与高空间分辨率的全色图像进行融合,得到与全色图像具有相同空间分辨率、与多光谱数据具有相同光谱分辨率的合成产物,提高了可见、近红外和短波红外波段的空间分辨率[3-5]。
目前,图像融合技术虽然用途广泛,涉及面广,但是还不够系统完善,一些方法也只是针对具体的应用环境提出的。本文针对水下复杂环境,提出一种改进的基于区域和能量的图像融合算法。对于提高水下运动目标与背景对比度,将目标物从复杂背景中分离出来,准确识别被测目标具有重要的意义。
1 光强图像和偏振图像的获取
偏振是光的基本性质之一,与普通光强相比,它包含了被测物的大量特征信息,一直是国内外研究的热点。偏振光的描述通常用Stokes矢量法来表示。即:

式中,S0或I代表光波的强度,即在不加检偏装置的情况下原始的光强信息;S1或Q代表光波的水平偏振分量与垂直偏振分量之差;S2或U代表光波沿45°方向的偏振分量与沿135°方向的偏振分量强度之差;S3或V代表光波的右旋圆偏振分量与左旋圆偏振分量的强度之差,近似为零[6]。
根据Stokes矢量计算线偏振度(Dolp)和偏振角(Aop)的公式分别为:

对于水下光强图像和偏振图像的获取,本文拟采用普通光强度相机和分焦平面相机分别对水下运动目标实时采集。为使实验效果显著,目标物选择玩具手枪射出的子弹,本实验在静水环境下进行。实验平台搭建完成,利用中型强光手电发出的自然光经过偏振片,波片后照射在运动物体上,通过图像采集装置分别采集光强图像和偏振图像。图1为水下光强图像和偏振图像采集原理图,主要由辅助光源系统和图像采集与处理系统两部分组成。

图1 水下光强图像和偏振图像采集原理图
图2为水下光强图像和偏振图像采集部分实物图,图(a)中左侧为光强度相机,右侧为分焦平面相机。

图2 水下光强图像和偏振图像采集部分实物图
图3、图4为偏振片旋转90°时,利用光强度相机和分焦平面相机分别采集到的第21帧时的水下运动目标的光强图像和偏振图像。图4为采集到的不同角度的偏振分量图像,与图3相比,图4更好的展现了目标物信息,对于图像的进一步处理,提供了较为准确的数据。

图3 水下光强图像

图4 水下偏振图像
图5是根据公式(1)计算得到的三个偏振分量图像。图6是根据3个偏振分量图像进一步解算出的线偏振度和偏振角图像,Dolp反映了图像的边缘轮廓信息,Aop反映了图像的表面特征信息,将二者进行融合有利于全面掌握图像的偏振特征,对于提取水下偏振图像的边缘信息具有重要作用。本文采用Toet融合方法,有利于突出原图像的特征部分。其融合公式为:

图5 I、Q、U分量图像

图6 线偏振度图像和偏振角图像
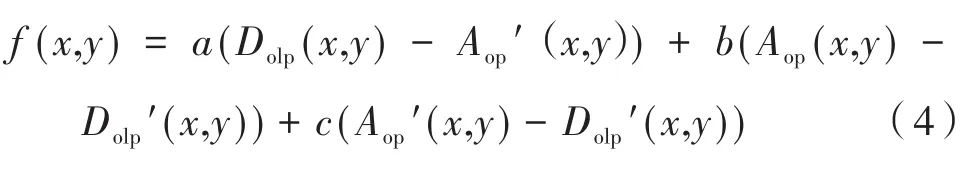
其中,a,b,c为权重因子,仿真实验表明,a,b,c分别取 0.6,0.2,0.2时,仿真效果最好;f(x,y)为Dolp与Aop融合得到的偏振特征图像Dolp-Aop;


图7 偏振特征图像Dolp-Aop
2 水下偏振图像融合
本文针对水下偏振图像成像质量差、易受水下环境干扰、边缘细节模糊等问题,提出一种改进的基于二维离散小波变换的图像融合算法,二维离散小波变换主要由离散小波分解与离散小波重构两个部分组成。二维离散小波分解主要通过采用选定的算法将源图像分解为低频图像与对角细节图像,通过查阅文献发现,小波分解的程度并非越深越好,分解的程度过深时,最底层的图像在融合的过程中,不可避免的会造成信息的丢失,通常这些丢失的信息是不可能被恢复的,因此本次实验将进行三层小波分解。二维离散小波重构是二维离散小波分解的逆过程,主要通过对二维离散小波分解的反演得到。
本文通过Mallat算法进行图像的三层小波分解与重构。Mallat算法主要是对图像的每一行、每一列进行滤波处理,而滤波通常借助一组低通滤波器和高通滤波器实现。每一层的小波分解均可得到图像的低频分量、水平细节分量、垂直细节分量、对角细节分量,其中低频分量涵盖了图像的主要特征,包含了源图像的大量能量,其他三个分量则包含了源图像的边缘细节信息[7]。其一尺度分解如图8所示。

图8 一尺度小波分解算法
图中An为低频图像,Hn为水平细节图像,Vn为垂直细节图像,Dn为对角细节图像,且An-1是An和Hn、Vn、Dn之和。图中H和G分别为低通和高通滤波器,当小波函数确定后即可推导低通和高通滤波器。1↓2表示降采样,水平方向二取一,2↓1表示降采样,垂直方向二取一。通过图8得到的是一尺度二维离散小波分解图像,尺度为三的二维离散小波分解可通过对低频图像进行三次小波分解得到,如图9(a)所示,图9(b)为经过三层小波分解后得到的一系列低频图像和细节图像。

图9 三尺度小波分解及分解系数显示
二维离散小波重构是分解的逆运算,其算法如图10所示。

图10 一尺度小波重构算法
2.1 改进的二维离散小波变换算法
由离散小波变换算法的原理可知,分解得到的低频分量和高频分量所包含的信息侧重点不同,针对低频分量和高频分量的特点,应采取不同的处理方法,融合方法的选择会有所不同,融合方法应该主要针对它们所包含的信息特点进行选择,这样才能保证最终得到的融合图像达到预期效果。
通过查阅文献发现,传统的图像融合算法通常采用加权平均法,大多应用在背景环境单一的情况下,优点是算法简单,易于实现,但是加权平均法没有详细分析原始图像各个频带的信息,融合出来的图像质量较差,带有很强的噪声,并且容易出现块状现象[8]。本文在综合各算法的优缺点后,提出一种改进的二维离散小波变换算法,用于对光强图像和偏振特征图像Dolp-Aop进行融合处理。
实验通过光强度相机采集光强图像,由分焦平面相机采集偏振图像,进一步处理得到偏振特征图像Dolp-Aop,对二者采用本文提出的一种改进的二维离散小波变换。具体算法步骤如下所示:(1)对光强图像和偏振特征图像Dolp-Aop进行配准处理,使光强图像和偏振特征图像Dolp-Aop达到像素级匹配;(2)分别对光强图像和偏振特征图像Dolp-Aop图像进行三层小波分解,根据低频分量和高频分量的特点,采用不同的融合规则。对第三层低频分量采用基于区域方差加局部能量相结合的融合规则,其他两层低频分量采用加权平均法。高频分量采用基于Sobel算子的融合方法;(3)将融合后的低频分量和高频分量进行二维离散小波重构,最终得到融合后图像。融合流程如图11所示。

图11 改进的二维离散小波变换流程
2.2 低频融合策略
低频分量与源图像最为接近,源图像的有用特征信息都集中在低频部分。对于低频分量常采用像素绝对值取大或取小法,这种方法算法简单,易于操作,常用于图像灰度差异不大的情况下,但是容易引入新的噪声,对比度也会得到削弱。为了更好的抑制噪声,避免产生新的噪声干扰,提高融合性能,本文拟采用一种基于区域方差加局部能量相结合的融合策略。假设M、N为光强图像和偏振特征图像经过小波分解后的低频分量,F为融合后的低频分量,则该方法的具体步骤为:
(1)分别计算M(x,y)和N(x,y)以点(x,y)为中心的3×3邻域内的区域方差,记为VarM(x,y)和

其中,Var为图像的某一邻域内的区域方差;S(x,y)代表图像在(x,y)点的像素值;(x,y)代表在邻域内的像素平均值;ω(a,b)代表窗口函数,且A×B的窗口大小为3×3邻域,窗口函数ω取为:
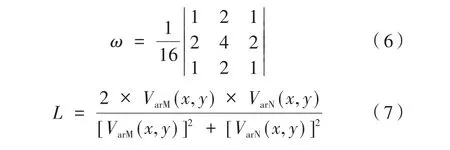
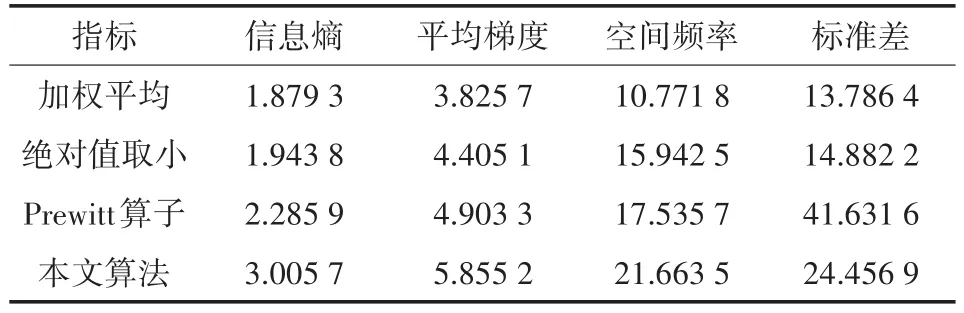
(2)当L 当L≥T时,根据式(9)计算像素点(x,y)周围3×3区域内的局部能量,分别记为EM(x,y)、EN(x,y)。 式中,E(x,y)是以(x,y)为像素中心点的区域局部能量;Q(x,y)为低频分量;w(x,y)表示以(m,n)为中心点时Q(x,y)对应的权重系数。 进一步计算两幅图像在融合后图像中的权重系数,记为WM和WN,如式(11)所示: 高频分量与低频分量不同,它包含的能量较少,所含信息较为分散,但是细节信息丰富,图像的边缘轮廓信息就包含在高频分量中。本实验选取的目标物为玩具手枪射出的长方形子弹,为准确识别目标物,对于其边缘轮廓的获取至关重要。边缘检测的方法有很多,每一种方法都有优缺点,需要视具体情况选择合适的方法。例如常见的Robert算子、Prewitt算子。Rob⁃ert算子是一个二阶矩阵,主要利用的是对两个对角线上的像素值作差来检测边缘,但是处理后的图像边缘不平滑,通常应用在噪声较少且边缘明显的情况下;Prewitt算子是一个三阶矩阵,它通常由水平边沿检测模板和垂直边沿检测模板组成,水平边沿检测模板通过对水平方向上的像素值作差来检测边缘;垂直边沿检测模板主要通过对垂直方向上的像素值作差来检测边缘。采用Prewitt算子检测边缘,对于噪声具有很好的平滑作用,使图像的边缘连续性得到加强,但是容易出现拼接现象。结合目标物的特征,本文对于高频部分的处理拟采用一种基于Sobel算子的融合策略[9]。 Sobel算子是一种一阶微分边缘检测算子,它的检测模板由三阶矩阵组成,与Robert、Prewitt算子不同的是,Sobel算子采用的是一种像素平均的方法,能够很好地抑制环境噪声的影响,更好的显示图像的边缘轮廓。同时,它还加入了像素权重的概念,Sobel算子认为与某一像素点距离不同的像素点,会对该像素点产生不同程度的影响,即距离越远,影响越小;距离越近,影响越大。Sobel算子能够使边缘连续性得到增强,从而突出图像的边缘轮廓,获得较好的边缘检测效果。 图12为Sobel算子的两组检测模板,分别为水平边缘检测模板、垂直边缘检测模板。计算时,分别将光强图像和偏振特征图像Dolp-Aop与两个矩阵作水平方向卷积和垂直方向卷积,即可得到图像的边缘轮廓,最终获得包含边缘轮廓信息的高频融合图像。 图12 Sobel算子边缘检测模板 将已经配准好的光强图像和偏振特征图像在matlab R2010b软件平台上进行仿真实验。为了更有效的验证本文提出的算法对图像的处理效果,分别采用基于加权平均法、像素绝对值取小法、参考论文[10]中提出的基于Prewitt算子的图像融合算法对图像进行融合处理,将得到的结果与本文提出的算法进行对比,实验结果如图13所示。 图13 实验仿真结果 由实验结果发现,图13(a)采用简单的加权平均法虽然消除了部分水体噪声的干扰,但是子弹的轮廓变得模糊,子弹身上出现块状现象,难以识别被测目标物;图 13(b)和图 13(c)是分别采用像素绝对值取小法、基于Prewitt算子的图像融合算法处理后的结果,可以看出融合图像亮度得到了一定的提升,显示了更多的边缘轮廓信息,但是还是存在一些环境噪声的干扰;图13(d)为本文算法得到的结果,观察发现,图像整体亮度得到明显提升,子弹与背景的对比度也得到加强,细节信息更加丰富,子弹上尾部凹槽已初步显现,子弹后端圆形尾部也可明显观察到。 对于融合图像的结果如果仅仅通过直观的观察来评价融合图像的质量,有时容易受到主观因素的干扰,不能客观反映事实。因此常引入一些客观评价指标,将主观判断与客观评价相结合,综合判断图像融合结果。本文拟采用信息熵、平均梯度、空间频率、标准差来评价融合结果。 四幅采用不同算法得出的图像评价指标值如表1所示。由表1数据发现,采用加权平均法得到的图像,反映其包含的信息量,图像的清晰度的指标都不理想,融合效果最差,相较于后三种算法,差距明显,这与之前直观观察融合图像的结论一致。基于Prewitt算子的图像融合得到的标准差最大,但是通过对比两幅融合图像发现,本文算法得到的图像包含的信息量更加丰富。而在信息熵、平均梯度、空间频率等指标方面,本文的算法都要优于其他三种算法。说明通过本文算法得到的融合图像对比度高,包含的信息量丰富,可以显现出更多的细节信息。 表1 图像融合评价指标 图像融合技术是近些年研究的热点,尤其是在医疗、军事等领域,例如水下军事目标的探测识别,未来将有广阔的前景。本文针对水下运动目标提出一种改进的二维离散小波变换,对于低频分量采用一种区域方差加局部能量相结合的图像融合算法,较好的保留了源图像的大部分信息;而对于高频部分,针对其含有的少量边缘轮廓信息,提出一种基于Sobel算子的图像融合方法。通过实验仿真,本文提出的算法相对于其他三种算法有一定的优势,融合图像显现出了更多的细节信息,这对于准确识别被测物有重要的意义。但是在实验过程中也发现,本文提出的算法会引入一些新的噪声,造成一些新的干扰,所以本文的算法还有待改善。

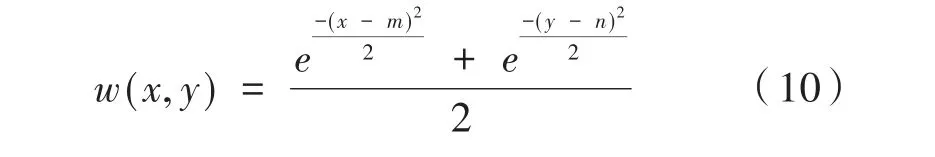

2.3 高频融合策略

3 实验结果与分析
3.1 融合结果分析

3.2 融合图像的评价指标
4 结论
