基于空间相关性的区域分布式光伏预测
2021-09-03孙树敏王士柏
李 宝,孙树敏,王士柏,程 艳,程 文
(1.山东理工大学电气与电子工程学院,山东淄博 255049;2.国网山东省电力公司电力科学研究院,山东济南 250003)
近年来国家对光伏行业的发展大力扶持,并采取了光伏扶贫项目、光伏发电领跑等一系列政策措施,使光伏行业取得了飞跃式的发展。与集中式光伏相比,分布式光伏尤其是建筑结合率高的分布式光伏更能被配电网接受。
分布式光伏对配电网的优化规划、电力系统电能质量、智能电网实时性保护都有较大影响[1]。因此,有效地预测分布式出力成为了电网规划运行的一项必要工作和热点研究问题。
常用的光伏预测方法有支持向量机、人工神经网络、马尔科夫链和多元回归分析等。这类方法依据大量的历史发电功率与历史气象记录来确保所建模型的准确性。而分布式光伏电站由于建造成本低、监管能力弱,导致其历史数据不多甚至缺少。所以,综上所述的方法很难直接应用在分布式电站出力预测上。
光伏电站输出功率数据与相同气象条件下的历史数据具有相似性,与相邻电站输出功率存在空间相关性[2]。因此,可由集中式光伏出力预测推算出与之相近区域内的分布式光伏的出力。文献[3]基于分层聚类算法对光伏电站间空间相关性进行判断及匹配,得到参考电站与目标电站间的映射关系,由BP 神经网络预测参考电站出力最终通过映射关系得到目标电站的出力。文献[4]则是将光伏出力分解为理想归一化曲线、幅值参数和随机分量,并提出利用典型日数据的理想出力提取方法,能够较好地表征多光伏电站间的空间相关性。文献[5]对分布式光伏系统的光伏发电数据之间的时空相关性进行了深入研究,提出了一种基于贝叶斯网络的预测模型。文献[6]将与目标电站强相关性的参考光伏序列作为LSTM 神经网络预测模型的输入部分,再结合目标电站NWP 数据与目标电站历史光伏数据预测分布式电站的出力。文献[7]依据无遮系数建立指标,聚类天气,然后通过copula函数建立各类天气下的预测模型,最终基于集中式光伏出力预测数据预测出分布式光伏出力并得出结论。
以上方法都是对单一分布式光伏电站出力进行预测,并没有对某一区域内分布式光伏电站进行预测。本文提出了一种基于空间相关性区域内分布式光伏预测方法。在同一区域理想的气象环境下,通过对区域内集中式电站与分布式电站空间相关性分析,将与集中式电站强相关性的所有分布式电站等效为虚拟集中电站,最终由集中式电站预测出力通过曲线拟合得到虚拟集中式电站出力。将虚拟集中式电站出力求和得到区域内分布式光伏出力。最后以我国北方某城市光伏电站数据为例,验证此方法的有效性,对光伏电站的部署及并网具有一定的实际意义。
1 光伏出力的空间相关性
对于分布在某一区域的光伏系统,对这些分布式光伏系统所收集的光伏数据进行空间相关性分析是非常有必要的。通过空间相关性分析,可以确定同一区域内不同位置的多个光伏系统的光伏输出模式的相似性,若将分析结果集成到光伏输出预测模型中,可以提高预测的准确性。
通常采用采样交叉相关函数(sample cross correlation function,SCCF)来计算参考点与目标点在当前时刻之前一段窗口内的实测光伏之间的相关系数[8]。本文用Xt、Yt表示分布式光伏电站在t时刻的光伏出力与集中式光伏电站在t时刻的光伏出力,对光伏时间序列(Xt,Yt),当k为延迟时间时,该函数可表示为:

式中:Cxx(0)为当延迟时间为0 时分布式电站与自身的相关性系数;Cyy(0)为当延迟时间为0 时集中式电站与自身的相关性系数;Cxy(k)为当延时为k时分布式光伏电站与集中式光伏电站的相关系数;n为时间序列的长度;XM和YM分别为Xt和Yt的平均值。由于对两点间的光照是同时发生的,故k取值为0。
|rxy|是一个小于等于1 的系数,用来表征同一区域内不同地点两段光伏序列之间相关性强弱。|rxy|值的增大表征相关性的增强,反之,|rxy|值的减小表征相关性的减弱。一般我们将|rxy|值大于0.8 时称为两段序列具有强相关性。
2 等效原则
根据区域内各自集中式光伏电站空间相关性强弱,对区域内分布式光伏电站进行聚类,然后将区域内分布式电站等效为多个虚拟集中式光伏电站。等效的虚拟集中式光伏电站的数量等于区域内集中式光伏电站数量。
将集中式光伏电站的气象监测设备作为中心,将区域内与各自集中式光伏电站空间相关性强度达到阈值的分布式光伏电站与各自集中式电站的气象中心等效为一虚拟集中式电站。即区域内有多少集中式光伏电站,就会有多少虚拟集中式电站。
虚拟集中式电站的历史气象数据使用由集中式电站气象监测设备监测所得数据,历史出力数据使用所形成虚拟集中式电站的分布式历史出力和。
若有某分布式电站与两个及以上集中式电站相关性强或者都达到阈值,将此电站归为与之相关性最强的集中式电站。
若有某分布式电站与区域内所有集中式电站相关性都没达到阈值,将之归为最近的集中式电站。
3 神经网络模型
在光伏预测中常用各种人工智能工具辅助(如神经网络),预测精度也得到了有效的提升。其中BP 神经网络作为最基础的神经网络算法被广泛研究。
BP 神经网络是单向传输网络的一种多层转发,由输入层、隐含层和输出层组成,实现了各层之间的完全连接。在信息正向传播时,数据由输入层输入经隐藏层后由输出层输出,前一层神经元的状态总会影响下一层神经元。当输出层的输出与所期望的输出误差很大时,误差开始进行反向传播,并通过预测误差对权重进行调整,使调整后的预测值接近期望值。
而本文所使用的自适应模糊推理系统(adaptive networkbased fuzzy inference system,ANFIS),其模型如图1 所示。
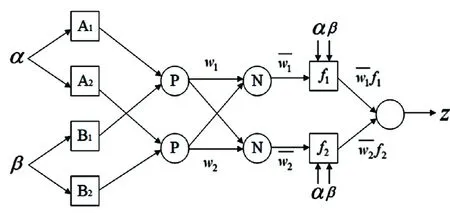
图1 ANFIS 模型
将第k层的第i个节点的输出设为Ok,i。
第一层:由节点函数表示各节点i。
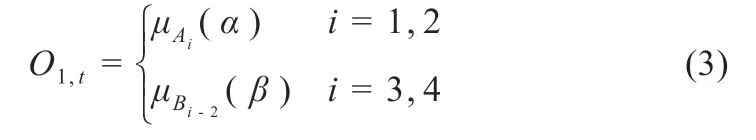
式中:O1,i为隶属度值;α、β为节点i的输入;Ai与Bi-2为与节点i相关的量。
第二层:P为这一层的节点,wi为模糊规则激励强度。
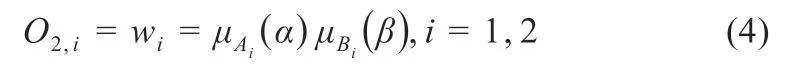
第三层:N为这一层的节点,将归一化处理。

第四层:f1、f2均为自适应节点,对模糊规则进行计算。

式中:pi、ri、qi均为后件参数。
第五层:该层的节点为固定节点,它是对所有输入进行计算的总输出。
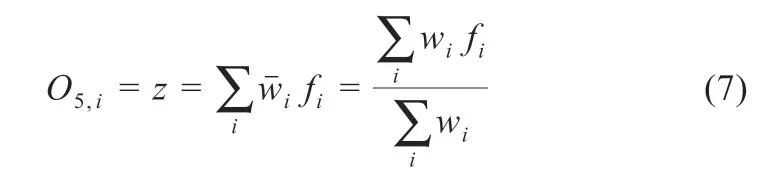
ANFIS 模型是由模糊推理系统与神经网络模型结合而成,其最大优点是既能防止在人工神经网络运行时的局部最优问题,又能补足传统模糊推理系统的缺点。
在此基础上,区域分布式光伏预测流程如下。
Step1:将区域内所有集中式电站与区域内所有分布式电站做空间相关性分析。
Step2:将与某一集中式电站相关性强的所有分布式电站等效为一虚拟集中式电站,即区域内集中式电站与等效而来的虚拟集中式电站数量相等。
Step3:将集中式光伏电站通过模糊神经网络方法(ANFIS)预测出力。
Step4:通过曲线拟合得出各虚拟集中式电站出力数据。
Step5:将各虚拟集中式数据求和得出该区域分布式出力数据。
4 算例分析
本文采取北方某地区光伏电站数据作为算例,电站分布如图2 所示,其中PV2、PV6 为集中式光伏电站,其余电站为分布式光伏电站。

图2 北方某区域8个电站空间分布
一般来说,空间相关性系数大于0.8 时,电站间表征为强相关性,如表1 所示,由于算例中所选区域不大,故电站间大体都呈现出强相关性。在这里,选取相关性系数0.85 作为等效阈值。

表1 8 个光伏电站空间相关系数
由表1 可知,与PV2 相关性系数大于等于0.85 的分布式电站为PV1、PV3 和PV4,与PV6 相关性系数大于等于0.85 的分布式电站为PV4、PV5、PV7 和PV8。由于PV4 与PV2 和PV6 的相关系数都达到阈值,故由前文中所述等效原则将PV1、PV3 和PV4 等效为虚拟集中式电站1 号,这里简称为XN1。将PV5、PV7 和PV8 等效为虚拟集中式电站2 号,这里简称XN2。由于虚拟集中式电站是由与集中式光伏电站相关性系数达到阈值的分布式电站等效而成,故我们可以推测等效而来的虚拟集中式电站也与所对应的集中式电站呈强相关性。将上述两对电站通过相关性分析得出表2所示结果。

表2 虚拟集中式电站空间相关性系数
由表2 可知,虚拟集中式电站确实与所对应的集中式电站呈现强相关性。
由于文中所述方法需要通过数据拟合的方式得到分布式光伏的出力,故对集中式光伏电站的预测精度要求较高。这里采取精度相对较高的ANFIS 预测方法对集中式电站出力进行预测。
现在对集中式电站PV2 使用文献[9]中所示ANFIS 实现短期光伏预测。采用集中式电站PV2 近2 个月的历史气象数据,历史出力数据作为输出的训练样本。根据训练样本,将太阳辐射、环境温度和历史出力数据作为输入,目标日出力作为输出。对该区域每日早上6 时至晚上7 时,每15 min 取一个样本,共计3 120 个样本。使用随机函数在数据样本中找出2 320 个数据作为训练样本,将其余800 个数据作为检验样本。训练次数设为200 次。在训练好预测模型后,对电站PV2 进行了检验预测。
由图3 可以看出预测结果与真实值之间偏差很小。由图4 可以看出,训练均方根误差(蓝色)为3.707,检验均方根误差(红色)为3.315。在训练次数达到100 次时,均方根误差(RMSE)就已经开始收敛了。因此,将该训练模型应用于集中式电站出力预测应能满足预测精度高。
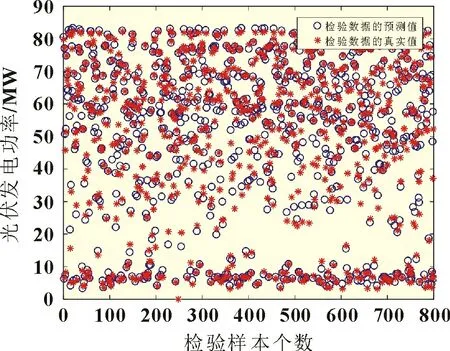
图3 检验预测误差
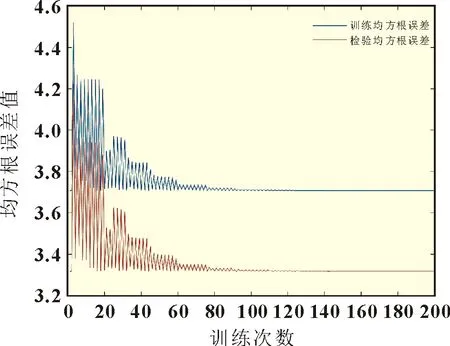
图4 均方根误差趋势
将目标日的气象数据、环境温度与历史出力数据作为输入,通过已训练好的训练模型,预测出集中式电站PV2 目标日出力。采用自适应模糊神经网络与BP-神经网络模型进行预测。从表3 可以看出,相比于BP-神经网络模型,采用ANFIS 预测模型的预测精度相对较高。
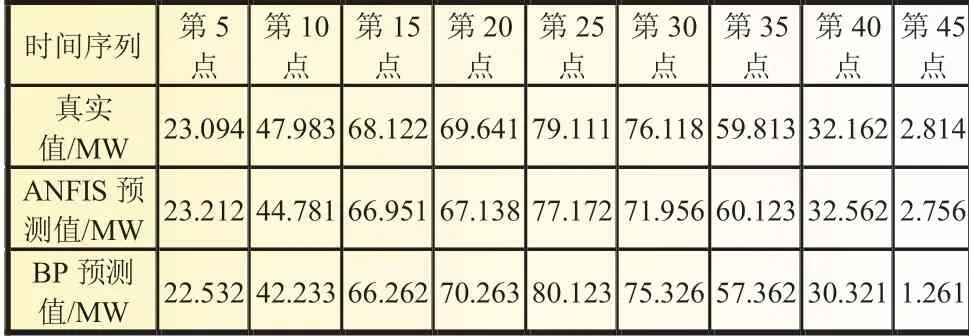
表3 集中式PV2 预测数据
在需要得到物理量之间的函数关系时,我们需要用到曲线拟合的方法。将集中式电站与其相关性强的虚拟集中式电历史出力进行数值拟合,就能得到两个电站间的空间相关性表达式,然后就可以通过对集中式光伏电站的预测推算出虚拟集中式电站的出力。通过由式(8)多项式拟合,可以由集中式电站PV2 目标日出力预测数据得到XN1 的预测出力:

式中:a=-0.000 013 77,b=0.000 484 9,c=0.249,d=-0.602 8;x为集中式电站出力;f(x)为虚拟集中式电站出力。由于夜间光伏出力为0,故可知当x=0 时,f(x)也为0。式中的系数并非固定不变,而是随着预测电站的变化而变化的。
由图5 可知,在通过集中式电站预测数据拟合得到XN1的预测值并将之与XN1 的实际值比较后,可以看出预测精度较高,这可能是因为所选电站地理位置相隔较近,加强了空间相关性的影响。

图5 虚拟集中式XN1预测出力曲线
同理可得,可以由集中式电站PV6 的预测出力得到XN2的预测出力,如图6 所示。
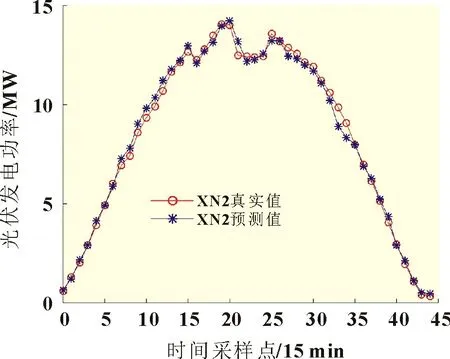
图6 虚拟集中式XN2预测出力曲线
然后,将XN1 与XN2 的预测出力求和,便得到所求区域内分布式光伏的出力。从图7 可以看出,本文所述方法最后预测出算例中区域分布式出力总和且精度较高,可能是因为算例中所选区域较小,空间相关性较强,其中电站间的出力序列极具相似性所致。当所选范围较大时,精度应该会适度下降。同时,本文所述方法能较好地预测出区域分布式光伏总出力,对于分布式光伏并网具有一定的实际意义。

图7 区域分布式总预测出力曲线
5 结论
本文提出了一种基于空间相关性区域分布式光伏出力预测方法。通过对区域内集中式电站与分布式电站的空间相关性分析将区域内分布式电站等效为若干虚拟集中式电站;采用了ANFIS 方法进行集中式光伏电站的出力预测;然后由多项式拟合,实现由集中式光伏电站出力预测到分布式光伏电站出力预测。通过光伏电站实例数据案例验证了该方法的有效性。
从预测条件上来看,当区域内电站数量越密集,得到的预测精度越高。而随着光伏行业的发展,分布式光伏将会越来越多地进入人们的生活,故该方法具有一定的参考价值。
