基于混合算法的光伏多峰值MPPT研究
2021-09-03郭昆丽刘璐雨蔡维正
郭昆丽,刘璐雨,蔡维正
(西安工程大学电子信息学院,陕西西安 710048)
光伏发电作为一种环保、无污染的发电方式受到了人们的关注,为了解决光伏发电系统能量转换效率低[1]的问题,最大功率点跟踪技术(maximum power point tracking,MPPT)是目前广泛应用和研究的技术。然而在实际运用过程中,光伏阵列会被物体遮挡(如建筑物、灰尘覆盖等),形成局部遮阴情况,从而引起局部过热。为了防止光伏阵列局部过热现象,通常在光伏电池板处反并联一个旁路二极管,但这会导致光伏阵列的输出特性P-U 曲线,出现多个峰值,使得传统的MPPT 算法失效[2]。
针对上述问题,文献[3]提出基于粒子群优化算法来搜寻多峰值情况的最大功率点。虽然该方法能够防止陷入局部最优点,但是单一的粒子群算法在粒子切换过程中会造成巨大的过冲和振铃现象,对开关器件造成损坏。文献[4]提出了采用人工神经网络方法用于MPPT 技术,但是神经网络的方法需要大量的历史数据来训练网络。文献[5]提出了一种基于电导增量法优化的粒子群全局MPPT 算法,将电导增量法同传统粒子群算法结合起来对光伏阵列进行联合控制。该方法的收敛速度比较慢,计算量比较大。文献[6]提出了一种基于“遮阴度”模型的新型多峰全局最大功率点跟踪重构算法,该方法对于复杂多变的遮阴现象,容易导致算法失效。文献[7]提出了扰动观察法结合模糊控制法,该方法在前期跟踪过程中使用扰动观察法,容易陷入局部最优值。
针对上述问题,本文提出了一种“两步走”MPPT 技术。首先利用粒子群算法(PSO)和遗传算法(GA)相结合的算法(PSO-GA)通过少量的迭代次数搜寻至最大功率点附近;然后切换至模糊控制方法来搜寻最大功率点,并稳定。这种混合算法弥补了单个算法的不足,提高了系统的速度和精度。通过粒子群算法和遗传算法优缺点互补,避免陷入局部最优值和减少收敛时间。通过模糊控制方法可以使系统在最大功率点处稳定,避免振荡带来的能量损失。
1 光伏阵列的输出特性
1.1 光伏阵列仿真模型
如图1 所示,用Simulink 搭建了光伏阵列在不同辐照度下的仿真模型。为了防止局部过热,在光伏电池处反并联了一个二极管。本文给出1 000、800、600 W/m2三种辐照度进行模拟局部遮阴情况。将温度设置为25 ℃,通过串联的方式将光伏阵列进行连接。
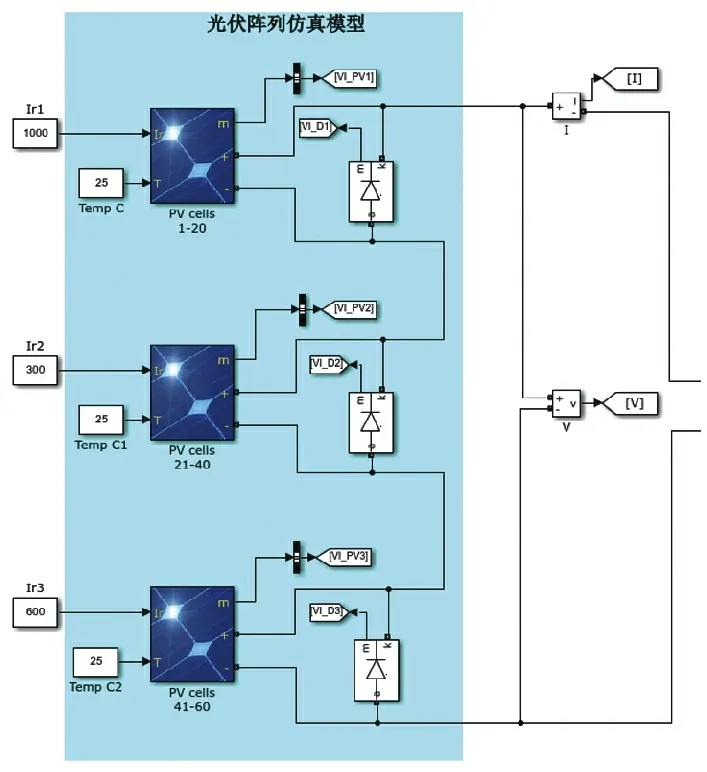
图1 光伏阵列局部遮阴仿真模型
1.2 光伏阵列输出特性曲线
对图1 中的光伏阵列模型进行仿真分析,得到输出电压、输出电流、输出功率的数据,进行绘图,得到光伏阵列的输出特性曲线,如图2 所示。因为外部环境条件的不断变化,所以P-U 曲线具有非线性特性。当温度或辐照度发生变化时,最大功率点也会发生移动。通过图2(b)可以观察得到,输出特性P-U 曲线出现了3 个峰值,当输出电压为20.88 V 时,才是全局的最大功率点,其余两个峰值点称为局部最大功率点。如果采用传统的MPPT 算法,比如扰动观察法,很难找到最大功率点,或者陷入局部最优点,造成能量损失,从而降低光伏发电的效率。

图2 局部遮阴情况下光伏阵列输出特性
2 混合算法
为了增加跟踪速度、减少算法计算量,本文采用“两步走”MPPT 控制策略。第一步,使用PSO-GA 结合算法,设定少量的迭代次数,找到全局最大功率点的范围区间。第二步,使用模糊控制在该区间内找到最大功率点,并且稳定,防止因为在最大功率点处振荡带来的能量损失。
2.1 PSO-GA 算法
采用粒子群算法和遗传算法相结合进行一个全局寻优搜寻。由于遗传算法的随机性,它不能提供问题的精确解,它需要复杂和耗时的计算才能收敛。相比之下,粒子群算法可以通过比较粒子的位置与周围位置以及粒子的全局位置来达到精确解。但是,如果使用不当,在高维空间中可能陷入局部最优。遗传算法通过交叉和变异得到各种解,弥补了粒子群优化算法的不足。同时,粒子群算法通过加快计算速度和提高计算精度来弥补遗传算法的不足[8]。为此,提出了一种粒子群和遗传结合的混合算法,如图3 所示。该算法具有粒子群优化算法的速度和精度以及遗传算法的多样性。
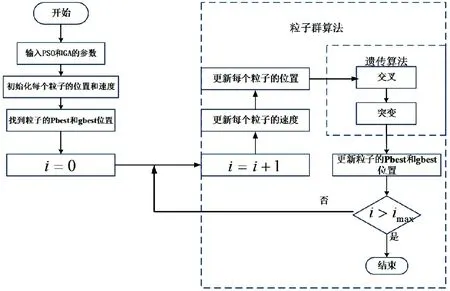
图3 PSO-GA混合算法流程
第一步,在搜索空间上随机生成初始解。粒子x0的初始位置也由[xmin,xmax]范围内的均匀分布生成,其中xmin和xmax分别为变量的上下界。
第二步,将粒子群算法应用于初始种群。每个粒子的位置和速度是根据单个粒子的经验和其他粒子的经验来确定的。该算法对结果进行排序,并保存用于快速收敛的最佳和最差解。对初始种群进行评估,并根据Pbest和gbest的值对种群进行排序。Pbest是每次迭代中的最佳解,gbest是所有迭代中的最佳解。
第三步,将遗传算法应用于剩余的低秩粒子。在每次迭代中,遗传算法通过交叉和变异操作生成一个新的种群。最后,将遗传算法和粒子群优化算法生成的种群组合起来,进行下一次迭代。这种组合被用作下一次迭代的初始解。算法将在特定的迭代次数后停止。
2.2 模糊控制
对于光伏系统,由1.1 节可知,太阳的辐照度和温度的变化都会影响光伏阵列的输出功率。而且这两个参数未知性很大,难以预测。与传统的MPPT 控制算法不同,模糊控制法对大气突变具有鲁棒性,不需要建立精确的数学模型。本文利用模糊控制算法进行MPPT,所提出的控制算法是离线控制算法,不需要依赖大量的数据学习[9]。本文以功率变化量与电压变化量之比为变化比率E,E(t)与上一个时刻E(t-1)的差值定义为ΔE,以E和ΔE这两部分作为模糊控制的输入,以占空比变化量ΔD作为输出。
在模糊控制算法中,由式(1)和式(2)计算模糊控制算法输入E和ΔE。

式中:PPV(t)和VPV(t)分别为光伏组件的输出功率和电压。
2.2.1 隶属度函数的确定
输入变量和输出变量的隶属度函数均采用三角形来定义。通过测量输入变量E和ΔE,并将数字表示形式的输入量量化为通常用语言值表示的某一限定码的序数。每一个限定码表示集合论域内的一个模糊子集。
第一步,辨识模糊控制的所有输入输出变量,其中横坐标为输入变量与输出变量相比的集合论域。纵坐标为隶属度函数,其范围为0~1。输入变量E和ΔE定义7 个模糊子集:负 大(NB)、负 中(NM)、负 小(NS)、零(ZO)、正 小(PS)、正 中(PM)、正大(PB),如图4(a)、(b)所示[10]。

图4 输入变量的隶属度函数定义
根据控制经验,将E和ΔE量化为离散论域,取值如下:

为了使最大功率点处有更小的抖动,本文设置ΔE的隶属度函数在越靠近最大功率点处,三角形隶属度函数越密集,反之越稀疏。
对于输出变量占空比ΔD也定义了7 个模糊子集:负大(NB)、负中(NM)、负小(NS)、零(ZO)、正小(PS)、正中(PM)、正大(PB),隶属度函数如图4(c)所示。
2.2.2 模糊规则设计
对于模糊规则的选取,按照“if and then”的原则来进行设计。根据控制经验,模糊规则设计如表1。

表1 模糊规则
对应Matlab 的模糊控制设计如图5 所示,“And”方法设置为min,“Or”方法设置为max,解模糊设定为重心法。根据表1 的模糊规则对应了49 条模糊规则语句,设定如图5 所示。
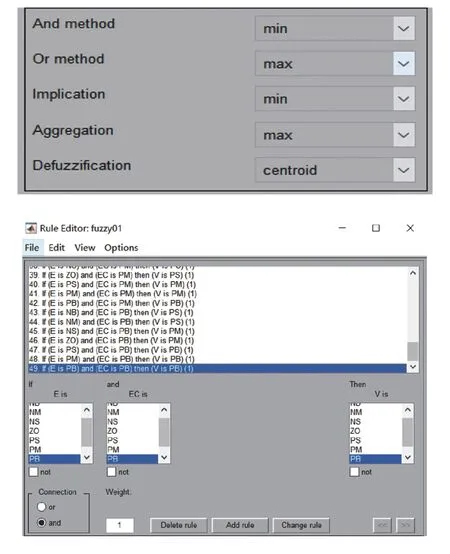
图5 Matlab模糊规则设计
3 仿真及实验结果
根据“两步走”MPPT 控制策略,搭建Simulink 仿真模型,如图6 所示。根据不断的实验测试,本文设定粒子群和遗传算法的迭代次数为30 次。可以减少计算量,并且能找到全局最大功率点附近,通过一个判断模块进行切换,转化为模糊控制搜寻至最大功率点,并稳定。
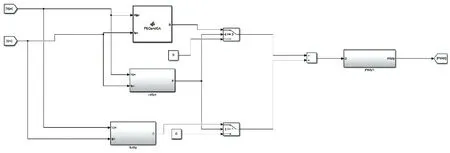
图6 “两步走”MPPT控制仿真模型
为了验证该方法提出的有效性,将基于扰动观察法、电导增量法、扰动观察结合模糊控制法,变步长电导增量结合粒子群算法,以及提出的混合控制算法进行了仿真对比验证。
在这种情况下,t=1 s时,辐照度从1 000 W/m2到800 W/m2,在t=1.5 s 时,辐照度变到600 W/m2,最后在t=2 s 时恢复到1 000 W/m2。如图7(a)所示,所提出的混合算法在t=0.2 s 时达到其最优点,扰动观察法和电导增量法分别在0.48 s 和0.54 s 时达到最优,这清楚地表明提出的混合算法在局部遮阴(光照幅度变化时)其性能优于电导增量法和扰动观察法。图7(b)显示了光伏系统输出功率的变化。所提出的混合算法可以在1 000 W/m2、25 ℃条件下使光伏阵列输出的功率达到98.70 kW,变步长增量结合粒子群算法可以达到96.03 kW,扰动结合模糊控制法输出功率为95.09 kW,电导增量法和扰动观察法输出功率分别为94.52 和90.13 kW。

图7 模糊控制算法隶属度函数的优化结果
根据分析,在不同的辐照度下出现多峰值情况,所提出的混合算法比另外几种更有优势,提高了输出功率,缩短了跟踪时间。如表2所示,当光照幅度在1 000 W/m2、25 ℃情况下,该算法比扰动结合模糊控制法提高了3.6%[(98.70-95.09)/98.70=3.6%],比变步长增量结合粒子群算法提高了2.7% [(98.70-96.03)/98.70=2.7%]。验证了本文所提出算法的优越性。
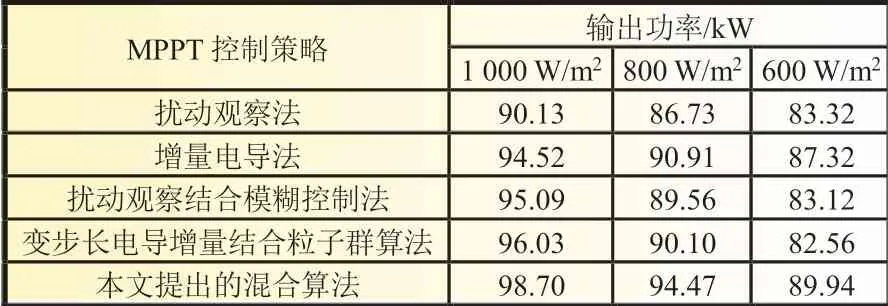
表2 变辐照度恒温度MPPT 控制算法的比较
4 结论
针对局部遮阴情况下出现的多峰值问题,本文提出了一种混合算法来跟踪全局最大功率点,从而提高光伏发电效率。采用“两步走”策略,首先利用粒子群结合遗传算法,使用少量的迭代次数搜寻至全局最大功率点附近;再切换至模糊控制算法,跟踪到最大功率点。利用Matlab/Simulink 仿真验证,该算法比扰动结合模糊控制法输出功率提高了3.6%,比变步长增量结合粒子群算法提高了2.7%,验证了该混合算法的可行性。通过跟踪时间对比,所提出的混合算法也有较优的跟踪性能和响应速度。
