基于自适应粒子群算法的MPPT控制策略
2021-09-03雷茂杰许坦奇孟凡英
雷茂杰,许坦奇,孟凡英,3
(1.中国科学院上海微系统与信息技术研究所,上海 200000;2.中国科学院大学,北京 100049;3.中国科学院大学材料与光电研究中心,北京 100049)
随着传统化石能源的日益枯竭,清洁环保的太阳能成为 能源领域的一个重要组成部分。太阳电池能够将太阳能转换为电能,当辐照度和温度变化时,太阳电池的输出电压和输出电流会发生变化,表现出非线性的输出特性[1]。为了提高光伏组件的转换效率,通过相应的控制策略使光伏组件始终工作在最大功率点上,这个过程就是最大功率点追踪(MPPT)。MPPT 技术已经成为光伏系统的重要组成部分,对于提高光伏组件的转换效率非常重要。
目前常用的MPPT 方法有恒压(CVT)法、扰动观察法(P&O)和电导增量法(INC),这些传统方法由于自身限制,无法兼顾追踪时间、追踪精度和响应速度的要求,且在有遮挡的情况下容易陷入局部功率最大点,无法追踪到全局最大功率点,造成极大的功率损失[2-4],因此阴影情况下的最大功率点追踪的研究变得尤为重要。
目前对阴影情况下的最大功率追踪的研究都聚焦在群体智能优化算法,粒子群算法作为一种全局算法,原理简单,全局搜寻能力强,在MPPT 上的应用非常广泛。但是传统的粒子群算法参数固定,存在震荡幅度大、收敛速度慢、依赖初始条件等问题[5]。本文提出了一种自适应粒子群算法,通过引入自适应参数算法和随机粒子,提升粒子群的收敛速度和整个算法的搜索精度。在Matlab/Simulink 平台上进行了固定辐照度和动态辐照度下的仿真实验,结果表明,本文提出的自适应粒子群算法在追踪时间、追踪精度及响应速度上有大幅的提升,在辐照度变化剧烈的条件下也具有非常好的追踪效果。
1 光伏组件仿真
1.1 太阳电池等效电路模型
太阳电池的等效电路模型如图1 所示。其中电流源表示光感电流,光感电流取决于电池的半导体材料特性,电流源与二极管和等效并联电阻Rsh并联,串上等效串联电阻Rs,I和Uoc为太阳电池的输出电流和输出电压,由太阳电池等效电路模型可知[6]:

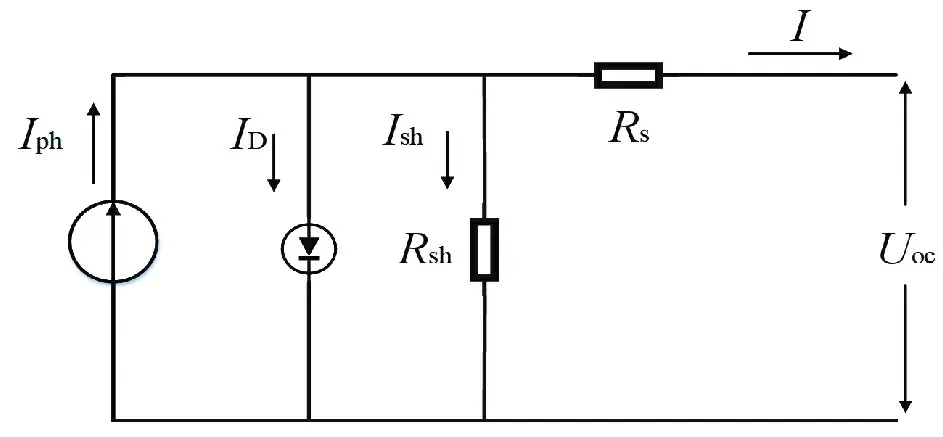
图1 太阳电池等效电路模型
太阳电池的I-U 输出特性表达式为:
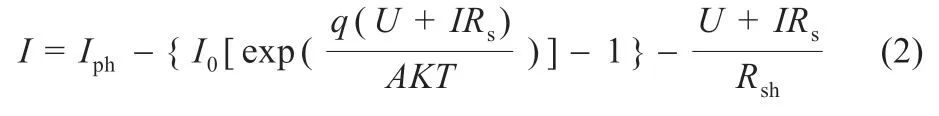
式中:U为太阳电池输出电压,V;I为太阳电池输出电流,A;Iph为光生电流,A;ID为二极管反向饱和电流,A;Ish为流过Rsh的电流,A;I0为反向饱和电流,A;q为电子电荷,C;K为玻尔兹曼常数;T为太阳电池工作绝对温度值,K;A为二极管理想因子;Rs为串联电阻,Ω;Rsh为并联电阻,Ω。
1.2 光伏组件建模
光伏组件的输出电压和电流会随着辐照度和温度的变化而变化,所以当辐照度和温度变化时,光伏组件的短路电流、开路电压、最大点电流和电压都会发生变化,有如下修正[7](SSTC=1 000 W/m2,TSTC=25 ℃)。
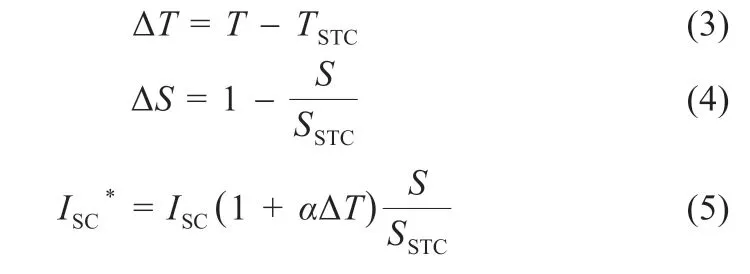

在标准条件下的辐照度和温度下,α=0.002 5,β=0.5,c=0.002 88。所选取的电池组件为SHJ 电池组件,组件版型为60 版,在标准条件下的参数如下:开路电压为44.686 V,短路电流为9.30 A,最大功率点处电压为36.920 V,最大功率点电流为8.59 A,最大功率为317.95 W。
1.3 遮挡条件下的光伏阵列建模
多个光伏组件串联起来就成为了光伏阵列,仿真建立3个光伏组件串联的光伏阵列,在实际情况中,由于光照角度和遮挡的问题会使遮挡区域的光伏组件输出的电流低于线路电流,此时被遮挡的光伏组件就成为了负载,造成输出功率降低。为了解决这种问题,每个光伏组件并联一个旁路二极管,但是旁路二极管加入导致了光伏阵列的多峰特性,在Matlab/Simulink 仿真平台分别仿真了无遮挡情况下温度不变(25 ℃)、辐照度变化的P-U 和I-U 输出曲线,如图2 所示;阴影情况下的P-U 和I-U 输出曲线,如图3 所示。

图2 无遮挡情况下光伏阵列在不同辐照度下的仿真
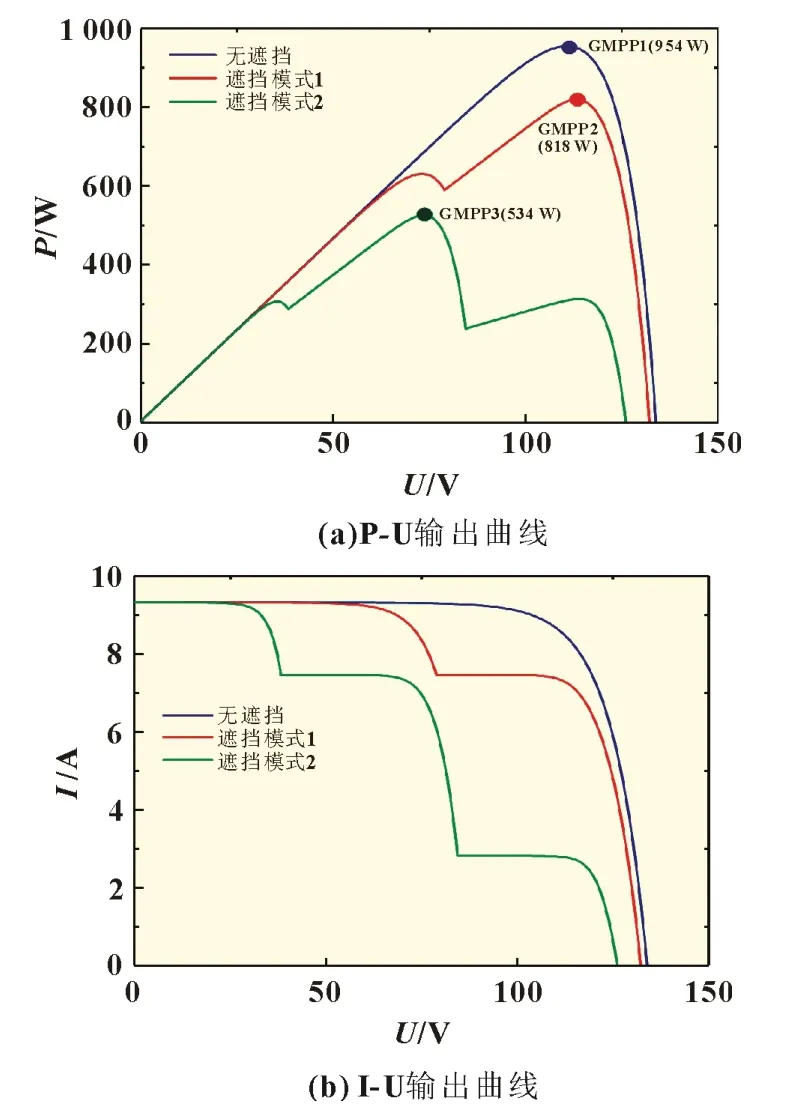
图3 阴影情况下光伏阵列在不同辐照度下的输出曲线
在阴影情况下设置了3 种模式进行对比:无遮挡模式、遮挡模式1 和遮挡模式2。
2 粒子群算法
2.1 粒子群算法提高全局搜寻能力
在遮挡的情况下,传统的算法由于自身的局限性,会陷入局部最大功率点,无法做到全局寻优,为了解决这一问题,引入粒子群算法进行寻优。粒子群优化算法(particle swarm optimization,PSO)是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。在N维搜索空间中,m个粒子构成一个粒子群X=(X1,X2,…,Xm),其中第i个粒子Xi=(xi1,xi2,…,xin)T,第i个粒子的速度为Vi=(vi1,vi2,…,vin)T,通过速度和位置不断的更新寻找个体极值和群体极值,从而逐步找到解空间的最优解。速度和位置更新公式为:

式中:ω为惯性权重;k为当前迭代次数;V为粒子的速度;c1、c2为加速度因子,初始值为2;pb、gb分别为个体最优值和群体最优值;r1、r2为(0,1)的随机数。
2.2 自适应粒子群算法提高搜寻速度和精度
普通的粒子群算法由于参数固定,对初始条件较为敏感,种群容易早熟,陷入局部最优解[8]。为了提高整个搜寻的效率,本文提出一种自适应粒子群算法,在普通粒子群算法的基础上随着迭代次数动态的改变参数,使其能够快速收敛,同时加入随机粒子进行遍历寻优。
对惯性参数和学习因子调整公式如下:

式中:ωmax=0.85,ωmin=0.5,c1_max=2,c1_min=1,c2_max=2,c2_min=1;k为迭代次数,kmax为最大迭代次数。
为了整体算法不陷入最优解,除了参数调整以外,还加入随机粒子,随机粒子选取为遍历选取,可以对这个搜寻区域均匀搜索,确保粒子群跳出局部最优解。
随机粒子的选取规则为:
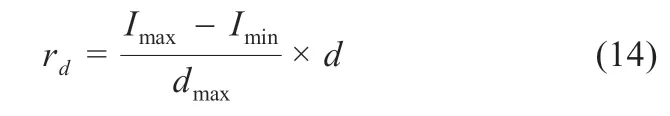
式中:Imax=9.30,Imin=3;d为随机次数,dmax为最大随机次数。
2.3 整体算法流程
在整个APSO 算法中,选取光伏阵列的电流作为飞行粒子,光伏阵列的总输出功率作为适应度函数,粒子种群数为4,最大迭代次数为50 次,最大随机迭代次数为20 次。为了应对光照幅度变化的情况,设置了重启条件[9]:的值在系统稳定时趋近于0,而当光照幅度变化时,输出功率会发生突变。在APSO 寻优算法结束后不断计算重启条件的值,满足重启条件后,会在新的条件下进行寻优,提升了变化环境下的寻找能力。
整体算法流程如图4 所示。
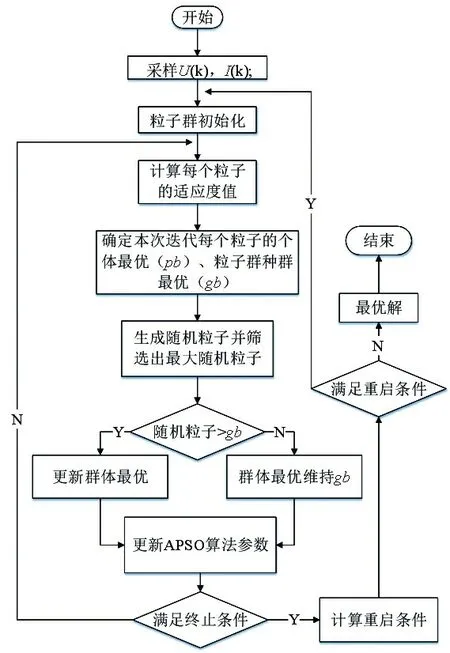
图4 基于APSO算法的MPPT流程
3 仿真验证分析
3.1 仿真平台
在Matlab/Simulink 仿真软件里搭建MPPT 的光伏系统对所提算法进行测试,选取Boost 型DC-DC 电路,光伏系统拓扑结构如图5 所示。MPPT 模块输出的是寻找到最大功率时的电压值,PWM 模块将电压转化为占空比信号作用在Q1上,实现电压的调控。
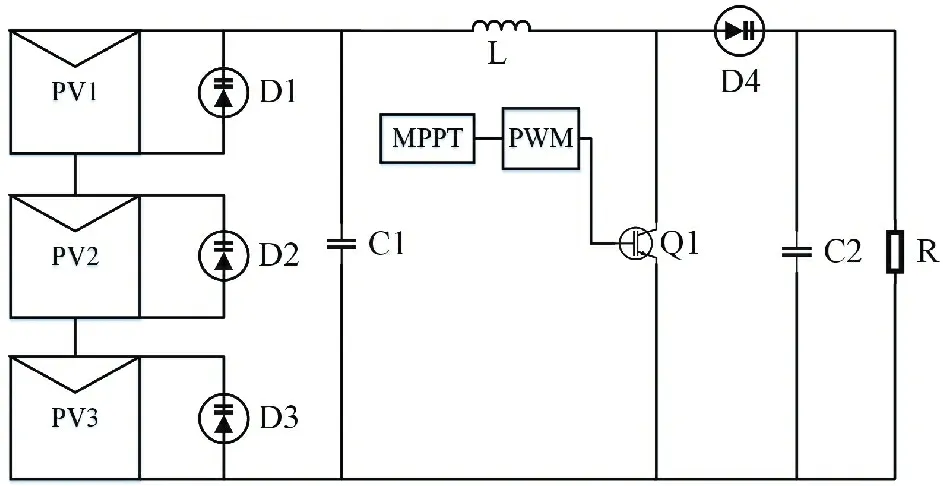
图5 光伏系统拓扑结构
3.2 固定条件下的仿真结果与分析
为了测试所提算法的优越性,进行了对比实验,将光伏阵列中PV1 的辐照度设为1 000 W/m2,PV2 的辐照度设为800 W/m2,PV3 的 辐照度设 为300 W/m2。分 别对INC 算法、传统PSO 算法和本文提出的APSO 算法进行仿真测试,其中INC 为固定步长,传统PSO 算法的参数为:c1=1.4,c2=1.4,ω=0.6。输出功率随着时间变化的结果如图6 所示,为了更直观地观察各种算法的追踪效果,将P-U 曲线也绘制在图6 中。

图6 三种算法在固定辐照度的功率输出曲线
从图6 中可以很明显地看出传统的INC 算法在阴影情况下无法追踪到最大功率点,陷入局部最大功率点2,追踪时间为0.34 s,追踪最大功率为327 W,追踪效率为61.2%。传统PSO 算法相较于INC 算法可以追踪到最大功率点,追踪时间也大幅缩短至0.14 s,追踪到的最大功率为521 W,追踪效率为97.5%,但是由于其参数固定,对群体最优解依赖度大,导致种群早熟并逐渐靠近第一次的最优解,所以不能完全达到最大功率点。所提出的APSO 算法收敛速度相较于普通粒子群算法更快,在追踪速度、精度和稳定性上均优于以上两种算法,追踪时间为0.035 s,稳定功率达到533 W,追踪效率为99.8%。
3.3 动态条件下的仿真结果与分析
为探究所提算法在动态辐照度条件下的追踪效果,在动态条件下对三种算法进行了测试。仿真时间为0.9 s,其中PV2 的辐照度每隔0.3 s 变化一次,依次为300、1 000、600 W/m2,PV1 保持1 000 W/m2不变,PV2 保持800 W/m2不变,绘制三种算法的输出功率随时间变化的波形,如图7 所示。
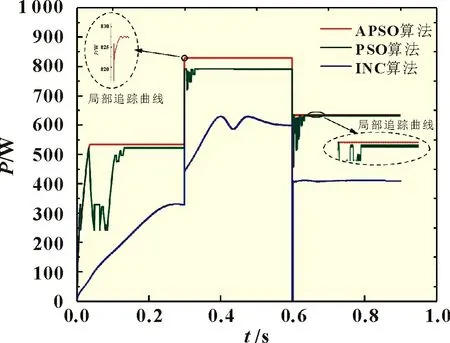
图7 三种算法在动态辐照度下的功率输出曲线
从图7 中可以看出在辐照度发生突变时,所提出的APSO算法相较于传统PSO 和INC 算法能够更快地寻找到最大功率点,输出功率更稳定,在辐照度变化的情况下适应能力更强。
4 结论
本文提出一种基于自适应粒子群算法的MPPT 控制策略,自适应粒子群算法克服了传统型算法在阴影条件下无法追踪到全局最大点,且追踪时间长、追踪精度差、响应速度慢的问题。相较于传统粒子群算法,通过引入自适应参数和随机粒子,加快了粒子群的收敛速度,提升了全局搜寻能力。在静态和动态条件下本文所提出的MPPT 方法在追踪时间、追踪精度、响应速度方面较前两种方法均有显著提升,最终实现了提高光伏组件转换效率的目的。仿真实验的结果表明,改进的MPPT 算法在辐照度变化剧烈的条件下依然具有优异的追踪效果,可为环境条件变化剧烈地区和有阴影地区的光伏系统设计提供参考。
