基于近似模型的板料成形稳健优化方法研究

孙远韬，陈凯歌，章增增，张 氢，秦仙蓉

（同济大学机械与能源工程学院，上海201804）

近年来，板料成形技术凭借其高效、高利用率等特点，在汽车、航空、航天等领域得到了极大的推广［1］。板料成形过程中，如果几何参数、成形工艺等选择不合理将会导致成形件发生破裂、起皱和回弹等缺陷，因此，成形过程中，有必要对设计及工艺方案进行优化。目前，针对板料成形的确定性优化技术已经取得了较为成熟的结果［2-4］。然而，工程实际中存在着诸如材料性能、冲压工艺等不确定性因素，最终影响着成形质量［10］。Sun等［5］针对汽车薄壁结构材料性能、冲压工艺等的不确定性，提出了一种多目标可靠性优化设计方法，提高了薄壁结构的成形质量。Ledoux等［6］将不确定性设计参数考虑为随机分布，对U型件的成型过程进行了可靠性分析和优化设计，并获得了较为满意的结果。研究结果表明，考虑不确定性的板料成形优化设计更能反映实际情况。

为进一步控制成形质量对不确定性因素的敏感程度，Aharon等［7］指出可采用稳健性优化设计方法。Li等［8］研究了成形参数偏差对响应方差的影响，解决了叠层钢板成形过程中工艺不确定性和材料性能变化导致的成型质量问题。Li等［9］针对冲杯过程提出了6σ的稳健设计方法，显著提高了成型质量的稳健性。Wiebenga等［10］将最大主应变作为目标函数，对杯冲进行3σ稳健性优化，提高了产品质量的稳健性。孙光永等［11］以破裂和起皱程度为目标函数，对汽车前地板角支撑板进行了稳健性优化。研究结果表明，采用稳健优化设计方法可以显著提高成形质量，避免成形质量的波动。

由于计算机辅助工程（Computer Aided Engineering，CAE）技术具有灵活、有效等优点，各国学者将其引入到板料成形中以预测响应［12-14］。然而，在采用CAE方法对板料成形进行优化设计时，存在优化效率低、成本大等问题。为了克服上述困难，近似模型与最优化技术结合的方法得到应用［15-16］。Naceur等［17］采用移动最小二乘法拟合了板料成形响应的近似模型，最终找到了较为满意的优化结果。卿启湘等［18］以行李箱盖成形为例，对比分析了Kriging模型与完全二次多项式响应面两种近似模型，并采用遗传算法优化得到了成形最佳工艺参数。对比分析可知，Kriging近似模型具有更高的建模效率、计算精度以及优化效率，并且更适用于大规模样本的拟合。

由上述分析可知，基于近似模型的板料成形稳健优化方法，提高了计算效率，同时保证了计算的精确度，且可以保证板料成形的缺陷最小、质量稳定可靠，本文基于Kriging近似模型的板料成形稳健优化方法如图1所示。

图1 基于Kriging近似模型的板料成形稳健优化方法Fig.1 Robust optimization method for sheet metal forming based on Kriging approximation model

1 基于替代模型的分析方法

近似模型是在实验设计的条件下，对输出响应的拟合。影响板料成形质量的设计变量通常较多，为了保证近似模型精度，同时提高计算效率，需要对各参数进行灵敏度分析以选出主要参数。

1.1 灵敏度分析

板料成形过程中，温度、摩擦系数、冲压速度和压边力等因素影响着成形质量，全面考虑所有参数并进行优化设计将导致优化效率低等问题。采用灵敏度分析法，可以优选出对板料成形质量影响较大的参数。

在进行灵敏度分析时，单个设计变量xi对设计响应yj的灵敏度Vij可以表示为

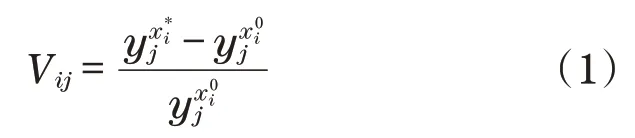
1.2 Box-Behnken设计

BBD（Box-Behnken Design）试验设计方法是由单纯二水平因子与不完全区块设计共同组成的，如图2所示。每个区块中，一定数量的因子通过所有的组合进行因子设计，其他因子保持中心值。图2为三因子BBD，其中包括3个区块，每个区块中2个因子作高低水平的4个可能组合，剩下的1个因子放在中心点。当因子数k等于3时，中心点通常需要重复3次，因此，最终试验总次数为4×3+3=15。

图2 三因子Box-Behnken设计布点示意图Fig.2 Layout of three factor box Behnken design

1.3 Kriging模型理论

Kriging模型是一种估计方差最小的无偏估计模型。该模型由回归模型f(x)和随机过程Z(x)组成，对于设计变量x与设计响应y(x)的一般数学表达式如下：

式中：f(x)=fT(x)β为多项式回归模型；f(x)=[f1(x)，f2(x)，…，fk(x)]T表示回归模型的基函数；β=[β1，β2，…，βk]T为 基 函 数 的 待 定 参 数；Z(x)为平稳的随机函数，用于修正模型的局部偏差。

记n个 样 本 点x1，x2，…，xn，其 响 应 为Y=[y1，y2，…，yn]T，在未知点x处，基于Kriging模型的响应预测估计值ŷ(x)为

式中：R为对称矩阵；R(xi，xj)为任意两个样本点xi和xj的互相关函数，常采用高斯互相关函数。

基函数的未知系数β̂根据加权最小二乘法得到

Kriging模型的最终表达式为

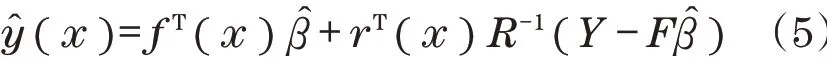
为了保证近似模型的精度，需要进行精度检验。常用的模型精度检验通常采用样本范围内的决定系数R2和相对均方根误差（RMSE）两种标准，其表达式为

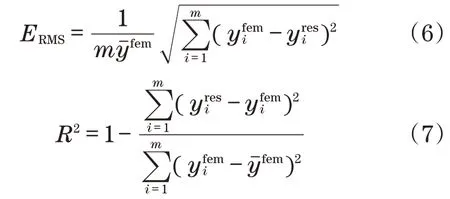
式中：ERMS为均方根误差；为有限元计算值；为近似模型计算值；为有限元计算的平均值。当RMSE的值接近0，R2的值接近1时，表明近似模型的误差很小。

2 板料成形回弹稳健性优化建模

稳健性设计的基本思路是通过最小化响应方差保证成形质量。回弹是板料成形的主要缺陷之一，一方面，回弹量越小，产品的成形质量就越高；此外，不确定性因素引起的回弹指标产生波动的减小有利于减少废品的数目。本文分别选取回弹量S的均值与标准差作为目标函数：

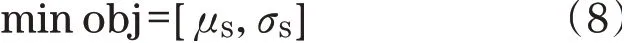
式中：S=y1(x)为设计变量与回弹量之间的Kriging近似模型。

工程中的不确定性因素大多可以用随机因素进行描述，采用随机模型描述稳健性优化的边界条件，需要使设计变量的约束边界满足一定的质量水平：

式中：、分别为设计变量的上下限；m由稳健性要求而定。

若xi服从随机正态分布，且当m=3时，则设计解的可靠度概率值约为99.7%。本文以回弹均值与方差作为优化目标，最终建立稳健性优化数学模型：

3 算例分析

板料的冲压成形条件不合理，会出现回弹、破裂和起皱等缺陷，分别用回弹量、最大减薄率和最大起皱高度进行衡量。包容式节点由板料在压力机上锻压成形，有利于提高桁架结构的极限承载能力并减少腹杆与弦杆的应力集中。考虑到上述3种成形缺陷，结合本文所提方法对包容式节点的成形缺陷进行分析并对回弹缺陷进行稳健优化设计。

3.1 灵敏度分析

根据工程实际，初选包容式节点成形参数如表1所示。

表1 包容式节点成形待选设计变量初值Tab.1 Initial value of design variables to be selected for the forming of bulge formed joint

对上述参数初值进行10%摄动，利用有限元分析求解变异后的响应结果，如表2所示。

表2 参数变异后包容式节点成形响应指标结果Tab.2 Results of forming response index of bulge formed joints after parameter variation

根据式（1），求解包容式节点成形参数对设计响应的灵敏度。为了综合考虑参数3种设计响应的影响，将同一参数对所有响应的灵敏度绝对值进行求和，如图3所示。最终得出灵敏度较大的4个设计参数，即为冲压速度、摩擦系数、板料初始温度和模具圆角。

图3 包容式节点成形设计参数对各响应的灵敏度值绝对值之和Fig.3 The sum of the absolute value of the sensitivity values of each response of the bulge formed joint design parameters

3.2 Box-Behnken设计

基于灵敏度分析，利用BBD可得如表3所示结果，考虑到各参数量纲不同，将各设计变量归一化处理，其中，x1，x2，x3，x4分别为冲压速度、模具圆角、摩擦系数和板料初始温度。

表3 BBD试验设计表Tab.3 BBD trial design table

在上述BBD设计表下进行有限元仿真，得到包容式节点的回弹量、最大减薄率（%）以及最大起皱高度（mm），分别用y1、y2和y3表示，如图4所示。

图4 BBD实验设计响应Fig.4 Response of BBD trial design

3.3 模型拟合与检验

基于试验样本数据，利用Matlab、对包容式节点成形响应进行Kriging近似拟合，并根据式（6）和式（7），检验其精度，结果如图5所示。

由图5可知，包容式节点成形各响应的Kriging近似模型的RMSE的值均逼近0，R2的值逼近1，具有较高的精度，可以可靠替代有限元模型进行后续优化设计。

图5 包容式节点成形近似模型精度评估图Fig.5 Accuracy evaluation chart of approximate forming model of bulge formed joint

3.4 稳健性优化

根据包容式节点成形工艺实际情况，并结合3σ稳健优化理论，建立包容式节点回弹控制的稳健优化数学模型如下：

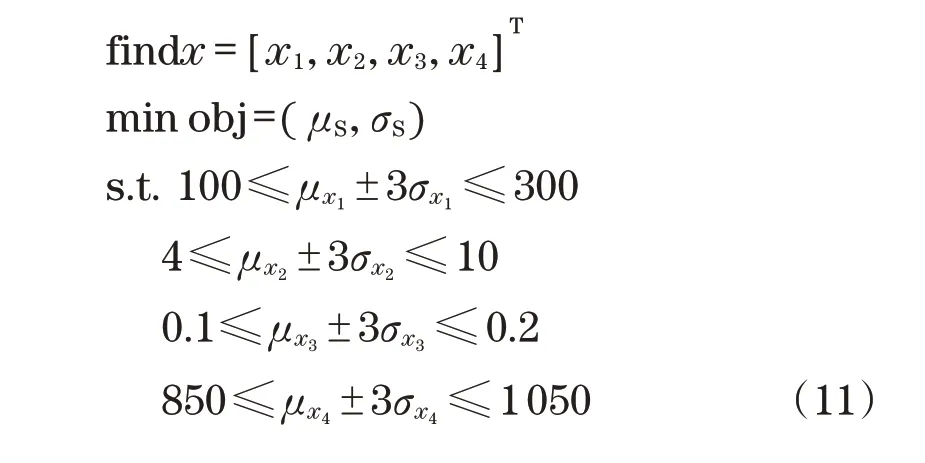
式中：x=[x1，x2，x3，x4]T为设计变量，各设计变量分别服从正态分布和对数正态分布，设计变量xi的上下边界则是根据3σ原则进行约束的。

根据最小距离法，对包容式节点回弹多目标优化问题进行求解。构造单目标函数（d=2）：

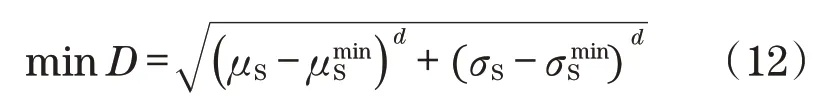
式中：μminS、σminS为单目标最优序列求解结果。

利用遗传算法进行求解，解得最小距离D为0.026 9，图6为优化迭代曲线。

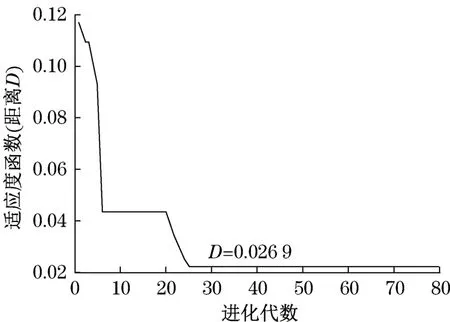
图6 优化迭代曲线图Fig.6 Optimization iteration curve

为了验证稳健优化的优越性，同时求解并给出了确定性优化设计方案，并对比两种方案的优劣。不同优化方法得到的回弹概率密度函数如图7所示。根据图7及实际经验可知，常规优化设计的优化目标更小的主要原因是，该方案最小化优化目标的方法是尽可能地用尽各设计变量的许用裕度，这将导致该设计方案的设计变量通常靠近或落在设计边界上，这将降低设计方案可行性。反之，稳健优化设计以回弹的均值与标准差为优化目标，在降低回弹量的同时，提高了回弹对外界的波动的抗干扰能力。

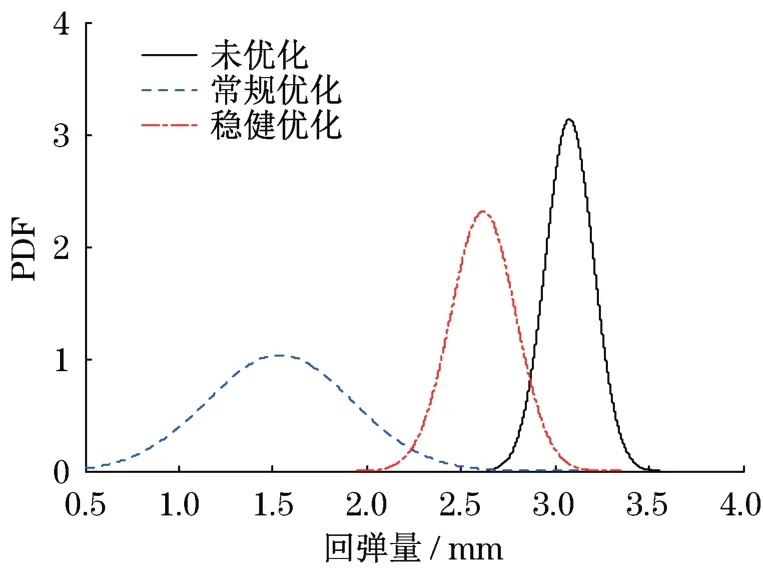
图7 回弹概率密度函数Fig.7 Probability density function of springback

4 结语

本文以包容式节点为对象，基于Kriging模型对其回弹量进行稳健优化。采用有限元法与Kriging模型拟合板料成形的近似模型。考虑工程实际中的不确定性，建立了板料成形稳健优化模型，对包容式节点进行稳健优化。所采用的BBD实验方法可以减少试验次数，节约实验成本，有利于提高计算效率。所构建Kriging近似模型拟合精度较高，可以有效地代替有限元分析。与确定性优化方案对比可知，稳健优化虽然略微牺牲优化目标，但减少了回弹缺陷，同时提高了回弹缺陷对外界的波动的抗干扰能力。本文所提方法为板料成形稳健优化设计与生产实际提供了理论参考。